内容补充页(相关公式解释)
from 学习日记_20241117_聚类方法(高斯混合模型)
学习日记_20241117_聚类方法(高斯混合模型)
公式 P ( Z = k ) = π k P(Z=k) = \pi_k P(Z=k)=πk
在高斯混合模型 (GMM) 中,公式 P ( Z = k ) = π k P(Z=k) = \pi_k P(Z=k)=πk 描述了选择某个高斯成分 k k k 的概率,其中 Z Z Z 是一个潜在变量(latent variable),表示数据点所属的成分。
详细解释
-
潜在变量 Z Z Z:
- Z Z Z 是一个离散随机变量,它的取值范围为 { 1 , 2 , … , K } \{1, 2, \ldots, K\} {1,2,…,K},其中 K K K 是模型中高斯成分的数量。每个 k k k 对应一个高斯分布。
-
权重 π k \pi_k πk:
- π k \pi_k πk 是与成分 k k k 相关的权重,表示在所有成分中选择成分 k k k 的概率。它满足以下条件:
- π k ≥ 0 \pi_k \geq 0 πk≥0(非负性)
- ∑ k = 1 K π k = 1 \sum_{k=1}^{K} \pi_k = 1 ∑k=1Kπk=1(归一化条件)
- π k \pi_k πk 是与成分 k k k 相关的权重,表示在所有成分中选择成分 k k k 的概率。它满足以下条件:
-
模型解释:
- 这个公式表明,在生成数据的过程中,根据权重 π k \pi_k πk,我们会选择其中一个成分 k k k。这个选择是随机的,但在长期来看,每个成分 k k k 被选择的概率正好等于其权重 π k \pi_k πk。
生成过程
在 GMM 的生成过程中,首先选择一个成分 $ Z $,然后在选择的成分下从对应的高斯分布中生成样本 $ X $。这个过程可以概述为:
-
从权重分布中选择成分 k k k:
P ( Z = k ) = π k P(Z=k) = \pi_k P(Z=k)=πk -
在选择的成分下,从该成分的高斯分布中生成数据:
X ∣ Z = k ∼ N ( μ k , Σ k ) X | Z=k \sim \mathcal{N}(\mu_k, \Sigma_k) X∣Z=k∼N(μk,Σk)
例子
假设我们有一个 GMM 模型,其中包含两个高斯成分(即 K = 2 K = 2 K=2),其权重分别为 π 1 = 0.6 \pi_1 = 0.6 π1=0.6 和 π 2 = 0.4 \pi_2 = 0.4 π2=0.4。这意味着:
- 有 60% 的概率选择成分 1,生成该成分下的样本。
- 有 40% 的概率选择成分 2,生成该成分下的样本。
总结
公式 P ( Z = k ) = π k P(Z=k) = \pi_k P(Z=k)=πk 是高斯混合模型的核心部分,定义了数据生成过程中选择每个高斯成分的概率。通过这些成分的加权组合,GMM 能够有效地建模复杂的分布结构。
公式 X ∣ Z = k ∼ N ( μ k , Σ k ) X | Z=k \sim \mathcal{N}(\mu_k, \Sigma_k) X∣Z=k∼N(μk,Σk)
公式 X ∣ Z = k ∼ N ( μ k , Σ k ) X | Z=k \sim \mathcal{N}(\mu_k, \Sigma_k) X∣Z=k∼N(μk,Σk)描述的是在给定潜在变量 Z Z Z 等于某个特定值 k k k 的情况下,随机变量 X X X 的条件分布。这里的含义可以分解为以下几点:
1. 条件分布
- X ∣ Z = k X | Z=k X∣Z=k 表示在选择了成分 k k k 的条件下生成的数据点 X X X。
- 这意味着我们只关注在成分 k k k 下生成的数据特性。
2. 高斯分布
- ∼ N ( μ k , Σ k ) \sim \mathcal{N}(\mu_k, \Sigma_k) ∼N(μk,Σk) 表示 X X X 服从均值为 μ k \mu_k μk、协方差矩阵为 Σ k \Sigma_k Σk 的多元高斯分布(或正态分布)。
- 均值 μ k \mu_k μk:这是成分 k k k 的中心位置,表示该成分的“典型”数据点。
- 协方差矩阵 Σ k \Sigma_k Σk:它描述了成分 k k k 的数据点的分布形状和方向。协方差矩阵的对角线元素表示不同特征的方差,而非对角线元素则表示特征之间的相关性。
3. 模型的生成过程
在高斯混合模型中,生成数据的过程可以总结为以下两步:
-
选择成分:
- 根据权重 π k \pi_k πk 随机选择一个成分 k k k。
-
生成样本:
- 一旦选择了成分 k k k,根据该成分的高斯分布生成数据点 X X X。这可以通过从高斯分布中抽样来实现。
举例说明
假设我们有两个高斯成分 K = 2 K=2 K=2:
- 成分 1: μ 1 = [ 2 , 3 ] \mu_1 = [2, 3] μ1=[2,3], Σ 1 = [ 1 0 0 1 ] \Sigma_1 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} Σ1=[1001]
- 成分 2: μ 2 = [ 5 , 7 ] \mu_2 = [5, 7] μ2=[5,7], Σ 2 = [ 2 0 0 2 ] \Sigma_2 = \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} Σ2=[2002]
在生成数据时:
- 以一定的概率(例如 π 1 = 0.6 \pi_1 = 0.6 π1=0.6, π 2 = 0.4 \pi_2 = 0.4 π2=0.4)选择成分。
- 如果选择成分 1,生成的数据点 X X X 将会满足:
X ∣ Z = 1 ∼ N ( [ 2 3 ] , [ 1 0 0 1 ] ) X | Z=1 \sim \mathcal{N}\left(\begin{bmatrix} 2 \\ 3 \end{bmatrix}, \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\right) X∣Z=1∼N([23],[1001])
这意味着生成的点将会在均值 [ 2 , 3 ] [2, 3] [2,3] 附近,并且具有单位方差,表示每个维度独立。
总结
公式 X ∣ Z = k ∼ N ( μ k , Σ k ) X | Z=k \sim \mathcal{N}(\mu_k, \Sigma_k) X∣Z=k∼N(μk,Σk)
是高斯混合模型的核心部分,描述了在选择特定高斯成分 k k k 的情况下数据的分布特性。通过不同成分的组合,GMM 能够灵活地捕捉复杂数据集的结构。
相关文章:
)
内容补充页(相关公式解释)
from 学习日记_20241117_聚类方法(高斯混合模型) 学习日记_20241117_聚类方法(高斯混合模型) 公式 P ( Z k ) π k P(Zk) \pi_k P(Zk)πk 在高斯混合模型 (GMM) 中,公式 P ( Z k ) π k P(Zk) \pi_k P(Zk…...

vue中动态渲染静态图片资源
不报错且f12查看元素的时候,显示的src说明已经渲染到html的src上,但是就是不显示在页面上 原因 在vue上,动态渲染静态图片资源(比如从assets文件夹加载的图片)需要注意打包工具对静态资源的解析方式 由于vue2的脚手…...

管伊佳ERP,原名华夏ERP,一个简约易上手的国产ERP系统
JSH_ERP(管伊佳ERP)是一款开源、模块化的企业资源计划系统,旨在为中小企业提供高效的管理工具。它基于SpringBoot框架和SaaS模式,支持进销存、财务、生产等业务模块,包括零售、采购、销售、仓库和报表管理。 核心特点…...

学习虚幻C++开发日志——委托(持续更新中)
委托 官方文档:Delegates and Lamba Functions in Unreal Engine | 虚幻引擎 5.5 文档 | Epic Developer Community | Epic Developer Community 简单地说,委托就像是一个“函数指针”,但它更加安全和灵活。它允许程序在运行时动态地调用不…...
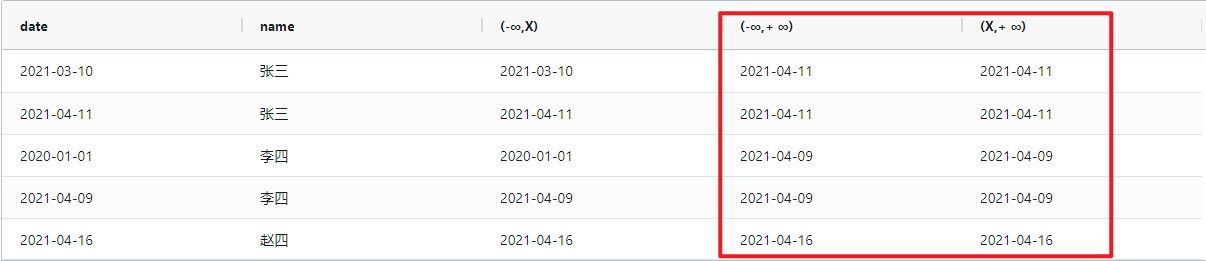
开窗函数 - first_value/last_value
1、开窗函数是什么? 开窗函数用于为行定义一个窗口(这里的窗口是指运算将要操作的行的集合),它对一组值进行操作,不需要使用 GROUP BY 子句对数据进行分组,能够在同一行中同时返回基础行的列和聚合列。 2、…...

「一」HarmonyOS端云一体化概要
关于作者 白晓明 宁夏图尔科技有限公司董事长兼CEO、坚果派联合创始人 华为HDE、润和软件HiHope社区专家、鸿蒙KOL、仓颉KOL 华为开发者学堂/51CTO学堂/CSDN学堂认证讲师 开放原子开源基金会2023开源贡献之星 「目录」 「一」HarmonyOS端云一体化概要 「二」体验HarmonyOS端云一…...

nodejs21: 快速构建自定义设计样式Tailwind CSS
Tailwind CSS 是一个功能强大的低级 CSS 框架,只需书写 HTML 代码,无需书写 CSS,即可快速构建美观的网站。 1. 安装 Tailwind CSS React 项目中安装 Tailwind CSS: 1.1 安装 Tailwind CSS 和相关依赖 安装 Tailwind CSS: npm…...

从JSON数据提取嵌套字段并转换为独立列的简洁方法
从JSON数据提取嵌套字段并转换为独立列的简洁方法 在数据处理和数据分析的日常工作中,我们经常遇到复杂的嵌套数据结构,特别是嵌入在JSON字段中的数据。这些数据往往需要解析并展开成独立的列,以便后续分析和建模。本文将详细介绍如何在Pyth…...

湘潭大学软件工程算法设计与分析考试复习笔记(四)
回顾 湘潭大学软件工程算法设计与分析考试复习笔记(一)湘潭大学软件工程算法设计与分析考试复习笔记(二)湘潭大学软件工程算法设计与分析考试复习笔记(三) 前言 现在是晚上十一点,我平时是十…...

特征交叉-DeepCross Network学习
一 tensorflow官方实现 tensorflow的官方实现已经是V2版本 class Cross(tf.keras.layers.Layer):"""Cross Layer in Deep & Cross Network to learn explicit feature interactions.Args:projection_dim: int,低秩矩阵的维度,应该小…...
stm32cubemx+VSCODE+GCC+makefile 开发环境搭建
title: stm32cubemxVSCODEGCCmakefile 开发环境搭建 tags: FreertosHalstm32cubeMx 文章目录 内容往期内容导航第一步准备环境vscode 插件插件配置点灯 内容 往期内容导航 第一步准备环境 STM32CubeMXVSCODEMinGWOpenOcdarm-none-eabi-gcc 然后把上面下载的软件 3 4 5 bin 文…...

Go语言中的Defer机制详解与示例
在Go语言中,defer是一个关键字,用于确保资源的清理和释放,特别是在函数中创建的资源。defer语句会将其后的函数调用推迟到包含它的函数即将返回时执行。这使得defer成为处理文件关闭、数据库连接释放、解锁等资源清理操作的理想选择。 Defer…...

H.265流媒体播放器EasyPlayer.js H5流媒体播放器如何验证视频播放是否走硬解
随着技术的不断进步和5G网络的推广,中国流媒体播放器行业市场规模以及未来发展趋势都将持续保持稳定的增长,并将在未来几年迎来新的发展机遇。流媒体播放器将继续作为连接内容创作者和观众的重要桥梁,推动数字媒体产业的创新和发展。 EasyPla…...

ms-hot目录
1. ms-hot1...

vulfocus在线靶场:骑士cms_cve_2020_35339:latest 速通手册
目录 一、启动环境,访问页面,ip:端口号/index.php?madmin,进入后台管理页面,账号密码都是adminadmin 二、进入之后,根据图片所示,地址后追加一下代码,保存修改 三、新开标签页访问:①ip:端…...

AI Large Language Model
AI 的 Large Language model LLM , 大语言模型: 是AI的模型,专门设计用来处理自然语言相关任务。它们通过深度学习和庞大的训练数据集,在理解和生成自然语言文本方面表现出色。常见的 LLM 包括 OpenAI 的 GPT 系列、Google 的 PaLM 和 Meta…...

React Native的`react-native-reanimated`库中的`useAnimatedStyle`钩子来创建一个动画样式
React Native的react-native-reanimated库中的useAnimatedStyle钩子来创建一个动画样式,用于一个滑动视图的每个项目(SliderItem)。useAnimatedStyle钩子允许你根据动画值(在这个例子中是scrollX)来动态地设置组件的样…...

FastJson反序列化漏洞(CVE-2017-18349)
漏洞原理 原理就不多说了,可以去看我这篇文章,已经写得很详细了。 Java安全—log4j日志&FastJson序列化&JNDI注入-CSDN博客 影响版本 FastJson<1.2.24 复现过程 这里我是用vulfocus.cn这个漏洞平台去复现的,比较方便&#x…...

【优选算法篇】分治乾坤,万物归一:在重组中窥见无声的秩序
文章目录 分治专题(二):归并排序的核心思想与进阶应用前言、第二章:归并排序的应用与延展2.1 归并排序(medium)解法(归并排序)C 代码实现易错点提示时间复杂度和空间复杂度 2.2 数组…...

C++:探索AVL树旋转的奥秘
文章目录 前言 AVL树为什么要旋转?一、插入一个值的大概过程1. 插入一个值的大致过程2. 平衡因子更新原则3. 旋转处理的目的 二、左单旋1. 左单旋旋转方式总处理图2. 左单旋具体会遇到的情况3. 左单旋代码总结 三、右单旋1. 右单旋旋转方式总处理图2. 右单旋具体会遇…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
