Leetcode 被围绕的区域

算法思想(解题思路):
这道题的核心是 将所有被边界包围的 'O' 保留下来,而将其他被围绕的 'O' 转换为 'X'。为了实现这一目标,我们可以分三步完成:
第一步:标记边界及其相连的 'O' 为特殊标记(例如 'E')
-
目标:
- 找到所有与矩阵边界相连的
'O',将它们和与它们直接相连的所有'O'标记为一个特殊字符(比如'E')。 - 这些
'O'是不能被包围的,因为它们直接或间接与边界相连。
- 找到所有与矩阵边界相连的
-
方法:
- 使用深度优先搜索(DFS)或广度优先搜索(BFS)从矩阵边界上的
'O'开始,向四个方向扩散,将与边界相连的'O'都标记为'E'。 - 这样,剩下的
'O'就是被完全包围的。
- 使用深度优先搜索(DFS)或广度优先搜索(BFS)从矩阵边界上的
第二步:遍历整个矩阵,处理不同状态的字符
-
目标:
- 将矩阵中所有剩下的
'O'转换为'X',因为这些'O'是被完全包围的区域。 - 将之前标记为
'E'的字符还原为'O',因为它们是不被包围的。
- 将矩阵中所有剩下的
-
方法:
- 遍历矩阵中的每一个元素,根据字符值进行判断:
- 如果是
'O',说明是被完全包围的区域,改为'X'。 - 如果是
'E',说明是边界或与边界相连的'O',改回'O'。
- 如果是
- 遍历矩阵中的每一个元素,根据字符值进行判断:
第三步:输出最终结果
经过上述处理,矩阵会满足题目要求,所有被包围的 'O' 转换为 'X',而没有被包围的 'O' 保留下来。
算法流程详解:
-
初始化矩阵大小:
- 首先判断输入矩阵是否为空。如果为空,直接返回。
-
标记边界:
- 遍历矩阵的 四个边界(第一行、最后一行、第一列、最后一列)。
- 对边界上的每个
'O',用DFS递归标记其相连的'O'为'E'。
-
遍历矩阵并修改字符:
- 遍历矩阵中的所有元素:
- 如果当前字符是
'O',说明它是被包围的,转换为'X'。 - 如果当前字符是
'E',说明它是与边界相连的,还原为'O'。
- 如果当前字符是
- 遍历矩阵中的所有元素:
时间与空间复杂度分析:
-
时间复杂度:
O(m * n)- 遍历矩阵的每个单元格一次,并且在标记边界时每个单元格也最多访问一次。
-
空间复杂度:
- 递归栈空间:使用DFS时,递归深度与矩阵的大小相关,最坏情况下需要
O(m * n)的栈空间。
- 递归栈空间:使用DFS时,递归深度与矩阵的大小相关,最坏情况下需要
示例说明:
输入:
board = [['X', 'X', 'X', 'X'],['X', 'O', 'O', 'X'],['X', 'X', 'O', 'X'],['X', 'O', 'X', 'X']
]
执行过程:
-
标记边界:
- 第一步遍历边界:发现
(3,1)是'O',并通过DFS标记与其相连的所有'O'为'E'。 - 标记后的矩阵:
[['X', 'X', 'X', 'X'],['X', 'O', 'O', 'X'],['X', 'X', 'O', 'X'],['X', 'E', 'X', 'X'] ]
- 第一步遍历边界:发现
-
遍历矩阵修改字符:
- 将所有未标记的
'O'转换为'X'。 - 将标记为
'E'的字符还原为'O'。 - 最终矩阵:
[['X', 'X', 'X', 'X'],['X', 'X', 'X', 'X'],['X', 'X', 'X', 'X'],['X', 'O', 'X', 'X'] ]
- 将所有未标记的
输出:
[['X', 'X', 'X', 'X'],['X', 'X', 'X', 'X'],['X', 'X', 'X', 'X'],['X', 'O', 'X', 'X']
]
总结:
通过将与边界相连的 'O' 特殊标记,我们可以有效区分哪些 'O' 是被围绕的,最终实现题目要求。
class Solution {public void solve(char[][] board) {if(board == null || board.length == 0) return;//获取矩阵的行和列int rows = board.length;int cols = board[0].length;for(int i = 0; i < rows; i++) {if(board[i][0] == 'O') {dfs(board, i, 0);}if(board[i][cols - 1] == 'O') {dfs(board, i, cols - 1);}}for(int j = 0; j < cols; j++) {if(board[0][j] == 'O') {dfs(board, 0, j);}if(board[rows - 1][j] == 'O') {dfs(board, rows - 1, j);}}//然后将剩下的O转换为X, E 转换回 Ofor(int i = 0; i < rows; i++) {for(int j = 0; j < cols; j++) {if(board[i][j] == 'O') {board[i][j] = 'X';}if(board[i][j] == 'E') {board[i][j] = 'O';}}}}private void dfs(char[][] board, int row, int col) {//首先检查是否越界if(row < 0 || row >= board.length || col < 0 || col >= board[0].length || board[row][col] != 'O') {return;}//将O标记为Eboard[row][col] = 'E';dfs(board, row + 1, col);dfs(board, row - 1, col);dfs(board, row, col + 1);dfs(board, row, col - 1);}
}
相关文章:

Leetcode 被围绕的区域
算法思想(解题思路): 这道题的核心是 将所有被边界包围的 O 保留下来,而将其他被围绕的 O 转换为 X。为了实现这一目标,我们可以分三步完成: 第一步:标记边界及其相连的 O 为特殊标记ÿ…...

ssm框架-spring-spring声明式事务
声明式事务概念 声明式事务是指使用注解或 XML 配置的方式来控制事务的提交和回滚。 开发者只需要添加配置即可, 具体事务的实现由第三方框架实现,避免我们直接进行事务操作! 使用声明式事务可以将事务的控制和业务逻辑分离开来,提…...

React第五节 组件三大属性之 props 用法详解
特性 a、props最好是仅限于父子上下级之间的数据传递,如果是祖孙多级之间传递属性,可以考虑使用props是否合适,或者使用替代方案 useContext() 或者使用 redux状态管理; b、props 中的属性是只读属性,如果想修改其中的…...

测评部署和管理 WordPress 最方便的面板
新版宝塔面板快速搭建WordPress新手教程 - 倚栏听风-Morii - 博客园 初学者使用1Panel面板快速搭建WordPress网站 - 倚栏听风-Morii - 博客园 可以看到,无论是宝塔还是1Panel,部署和管理WordPress都有些繁琐,而且还需要额外去配置Nginx和M…...

【系统分析师】-2024年11月论文-论DevOps开发
1、题目要求 论Devops及其应用。Devops是一组过程、方法与系统的统称,用于促进开发、技术运营和质量保障部门之间的沟通,协作与整合。它是一种重视软体开发人员和工厂运维技术人员之间沟通合作的模式。透过自动化“软件交付”和“架构变更”的流程&…...

算法【子数组最大累加和问题与扩展】
子数组最大累加和问题是一个非常经典的问题,也比较简单。但是扩展出的问题很多,在笔试、面试中特别常见,扩展出的问题很多非常有趣,解法也比较巧妙。 下面通过一些题目来加深理解。 题目一 测试链接:https://leetcode…...

小程序23-页面的跳转:navigation 组件详解
小程序中,如果需要进行跳转,需要使用 navigation 组件,常用属性: 1.url :当前小程序内的跳转链接 2.open-type:跳转方式 navigate:保留当前页面,跳转应用内的某个页面,…...

AI社媒引流工具:解锁智能化营销的新未来
在数字化浪潮的推动下,社交媒体成为品牌营销的主战场。然而,面对海量的用户数据和日益复杂的运营需求,传统营销方法显得力不从心。AI社媒引流王应运而生,帮助企业在多平台中精准触达目标用户,提升营销效率和效果。 1.…...

【Node.js】全面解析 Node.js 安全最佳实践:保护您的应用
Node.js 是一种强大的 JavaScript 运行时,广泛用于构建现代 Web 应用和 API。然而,由于其开放性和异步特性,Node.js 应用容易受到多种安全威胁的攻击,比如 SQL 注入、跨站脚本 (XSS) 和拒绝服务攻击 (DoS)。在本文中,我…...

Docker 用法详解
文章目录 一、Docker 快速入门1.1 部署 MYSQL1.2 命令解读: 二、Docker 基础2.1 常见命令:2.1.1 命令介绍:2.1.2 演示:2.1.3 命令别名: 2.2 数据卷:2.2.1 数据卷简介:2.2.2 数据卷命令ÿ…...
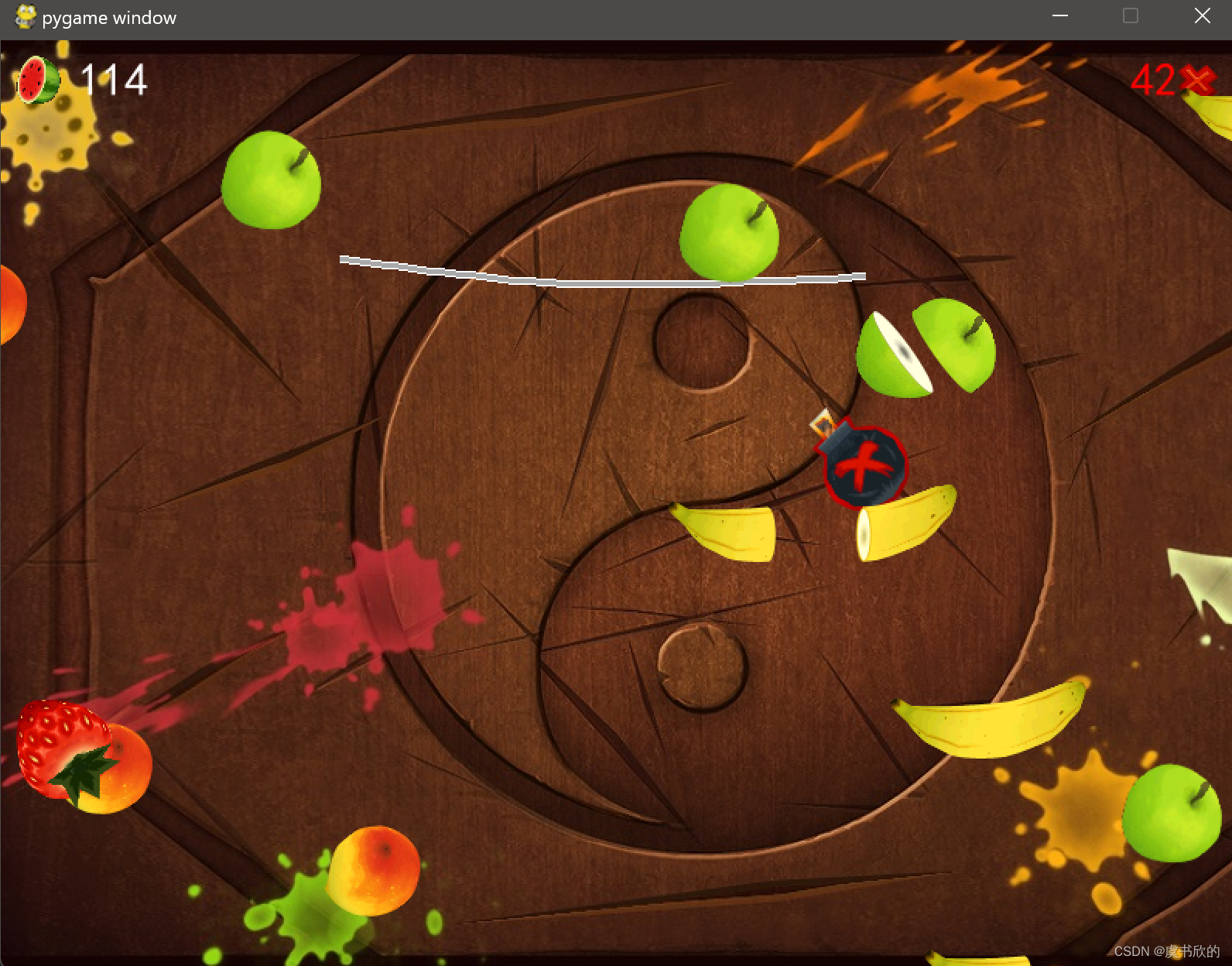
Python小游戏28——水果忍者
首先,你需要安装Pygame库。如果你还没有安装,可以使用以下命令进行安装: 【bash】 pip install pygame 《水果忍者》游戏代码: 【python】 import pygame import random import sys # 初始化Pygame pygame.init() # 设置屏幕尺寸 …...

Kafka Offset 自动提交和手动提交 - 漏消费与重复消费
目录 1. 引言 2. Offset 提交方式概述 2.1 自动提交 Offset 2.2 手动提交 Offset 3. 漏消费与重复消费的问题分析 3.1 自动提交模式下的漏消费和重复消费 漏消费 重复消费 3.2 手动提交模式下的漏消费和重复消费 漏消费 重复消费 4. 自动提交与手动提交的选择 4.1…...

Vue3父组件和子组件
子组件暴露方法给父组件,父组件传值 子组件 const editCalendar (value: string) > {console.log(获取父组件的值, value)};//暴露给外部调用defineExpose({editCalendar,}); 父组件 <template> <CalendarEdit ref"editRef" /> </…...

Linux 定时任务全解析
文章目录 一、Cron 服务1.1安装1.2配置文件格式1.3使用方法1.4系统级与用户级 Cron 任务区别 二、At 服务2.1安装2.2工作原理2.3使用方法 一、Cron 服务 1.1安装 在大多数 Linux 发行版中,Cron 服务通常已经默认安装。例如在 Ubuntu 系统中,可以通过以…...

XLNet——打破 BERT 局限的预训练语言模型
近年来,深度学习在自然语言处理(NLP)领域取得了革命性进展,其中 BERT 的出现标志着双向语言建模的强大能力。然而,BERT 也存在一些局限性,限制了其在生成任务中的表现。2019 年,由 Google 和 Ca…...
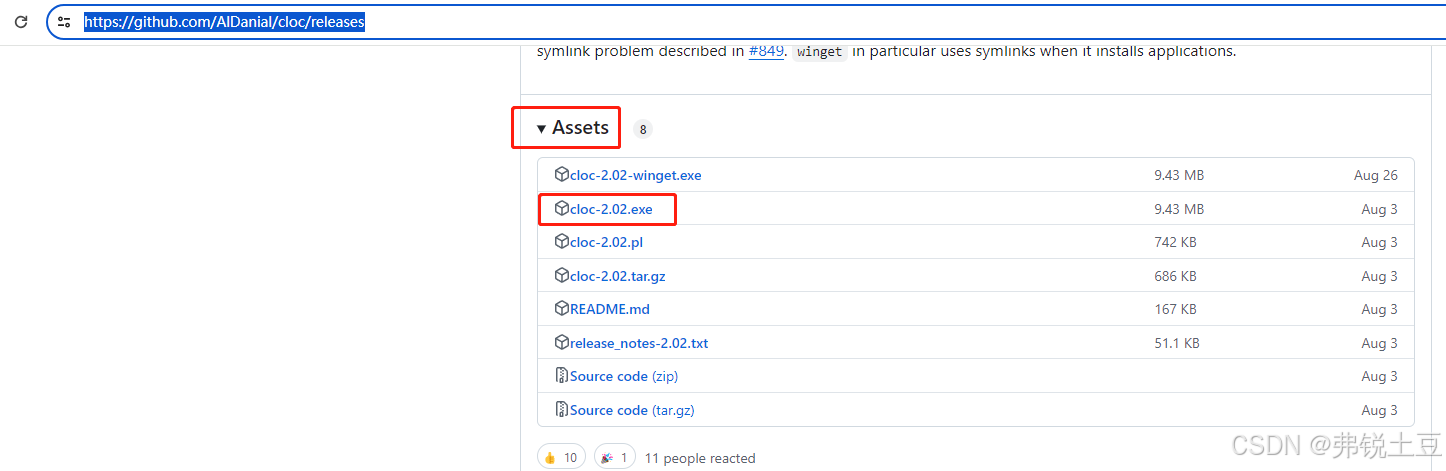
开源代码统计工具cloc的简单使用
一.背景 公司之前开发了个小系统,要去申请著作权,需要填写代码数量。应该怎么统计呢?搜索了一下,还是用开源工具cloc吧!我的操作系统是windows,代码主要是java项目和vue项目。 二.到哪里找 可以去官方下载…...

如何创建一个项目用于研究element-plus的原理
需求:直接使用element-plus未封装成组件的源码,创建一个项目,可以使用任意的element-plus组件,可以深度研究组件的运行。例如研究某一个效果,如果直接在node_modules修改elment-plus打包之后的那些js、mjs代码…...
单片机进阶硬件部分_day2_项目实践
设计要求 从绘制原理图到画PCB板,完成智能云衣柜项目 STM32 (Modbus)云IOT衣物云端管理 华为PCB布线规范 基于IoT的智享家主控系统 步骤分析 需求分析 器件选型绘制原理图(器件连接)PCB布局、布线泪滴、铺铜、添加丝印…...
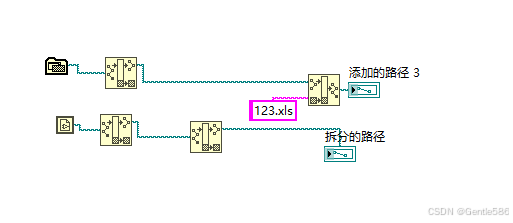
labview关于文件路径的问题
在调用文件或拆分文件的时候经常会用到拆分路径函数和创建路径函数,最常用的也是当前应用程序目录或者是当前VI目录。 这里我们看到应用程序目录和VI目录在同一项目中,应用程序目录更像是根目录,往下拆分成了各个VI的子目录。 接下来我们来拆…...
72项!湖北省2024年度第二批省级科技计划项目拟立项项目公示!
本期精选 SCI&EI ●IEEE 1区TOP 计算机类(含CCF); ●EI快刊:最快1周录用! 知网(CNKI)、谷歌学术期刊 ●7天录用-检索(100%录用),1周上线; 免费稿件评估 免费匹配…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...
