基于 NCD 与优化函数结合的非线性优化 PID 控制
基于 NCD 与优化函数结合的非线性优化 PID 控制
1. 引言
NCD(Normalized Coprime Factorization Distance)优化是一种用于非线性系统的先进控制方法。通过将 NCD 指标与优化算法结合,可以在动态调整控制参数的同时优化控制器性能。此方法特别适合非线性和复杂系统,解决传统 PID 控制在强耦合、非线性环境下的适应性不足问题。
2. 控制方法框架
2.1 基本思想
-
目标:
最小化系统的 NCD 指标,优化 PID 控制器性能。 -
核心思想:
利用优化算法(如梯度下降、遗传算法或粒子群算法)对 PID 参数 Kp,Ki,Kd进行实时调整,使得系统误差和扰动的影响最小化。

3. 系统框图
控制系统包括以下模块:
- PID 控制器:提供初始控制信号。
- 非线性被控对象:复杂动态系统。
- NCD 指标计算器:实时计算系统性能指标。
- 优化模块:基于优化算法调整 PID 参数。

5. C++ 实现
以下为基于 C++ 的优化 PID 控制代码示例。
5.1 PID 控制器
class PIDController {
public:double Kp, Ki, Kd; // PID 参数double Ts; // 采样周期double integral, prevError; // 积分项和前次误差PIDController(double kp, double ki, double kd, double ts): Kp(kp), Ki(ki), Kd(kd), Ts(ts), integral(0.0), prevError(0.0) {}double compute(double error) {integral += error * Ts;double derivative = (error - prevError) / Ts;prevError = error;return Kp * error + Ki * integral + Kd * derivative;}
};
5.2 NCD 指标计算
double computeNCD(double Tw, double Sw) {return sqrt(Tw * Tw + Sw * Sw);
}
5.3 优化算法(梯度下降
class Optimizer {
public:double learningRate;Optimizer(double lr) : learningRate(lr) {}void updateParameters(double& Kp, double& Ki, double& Kd,double dJ_dKp, double dJ_dKi, double dJ_dKd) {Kp -= learningRate * dJ_dKp;Ki -= learningRate * dJ_dKi;Kd -= learningRate * dJ_dKd;}
};
5.4 主程序
int main() {// 初始化 PID 控制器和优化器double Ts = 0.01;PIDController pid(1.0, 0.5, 0.1, Ts);Optimizer optimizer(0.01);// 初始参数double Tw = 0.0, Sw = 0.0, e = 0.0; // 传递函数、灵敏度函数、误差double Kp = 1.0, Ki = 0.5, Kd = 0.1;for (int iter = 0; iter < 100; ++iter) {// 模拟系统响应,更新 Tw 和 SwTw = 1.0; // 示例值(需通过模型计算)Sw = 0.5; // 示例值(需通过模型计算)e = 0.1; // 示例误差// 计算目标函数double J = computeNCD(Tw, Sw) + e * e;// 梯度计算(这里用伪梯度作为示例)double dJ_dKp = 0.01 * Kp; // 示例值double dJ_dKi = 0.01 * Ki; // 示例值double dJ_dKd = 0.01 * Kd; // 示例值// 更新 PID 参数optimizer.updateParameters(Kp, Ki, Kd, dJ_dKp, dJ_dKi, dJ_dKd);// 打印迭代信息std::cout << "Iter: " << iter << ", J: " << J<< ", Kp: " << Kp << ", Ki: " << Ki << ", Kd: " << Kd << std::endl;}return 0;
}
6. 特点与优势
-
动态优化: 实现了基于系统实时性能的动态优化,适应非线性环境。
-
自适应性: PID 参数实时调整,适应系统动态特性变化。
-
鲁棒性: 通过 NCD 指标约束,提高了系统的抗干扰能力。
-
通用性: 可结合遗传算法、粒子群优化等优化方法,适应不同场景需求。
7. 应用场景
- 复杂非线性系统控制:如化工过程控制、非线性伺服控制。
- 机器人控制:多自由度运动控制。
- 自动化工业控制:多变量耦合系统优化。
- 智能交通:非线性动力学建模与控制。
8. 总结
基于 NCD 与优化函数结合的非线性优化 PID 控制方法,结合了经典控制与现代优化技术的优点,适合在非线性、动态复杂的系统中实现高性能控制。未来可以扩展到多变量控制、分布式控制等领域,进一步提升系统效率与稳定性。
相关文章:

基于 NCD 与优化函数结合的非线性优化 PID 控制
基于 NCD 与优化函数结合的非线性优化 PID 控制 1. 引言 NCD(Normalized Coprime Factorization Distance)优化是一种用于非线性系统的先进控制方法。通过将 NCD 指标与优化算法结合,可以在动态调整控制参数的同时优化控制器性能。此方法特别…...

【数据分析】基于GEE实现大津算法提取洞庭湖流域水体
大津算法提取水体 1.写在前面2.洞庭湖水体识别1.写在前面 最大类间方差法,也称为Otsu或大津法,是一种高效的图像二值化算法,由日本学者Otsu于1979年提出。该算法基于图像的频率分布直方图,假设图像包含两类像素(前景和背景),并计算出一个最佳阈值,以最大化类间方差,从…...
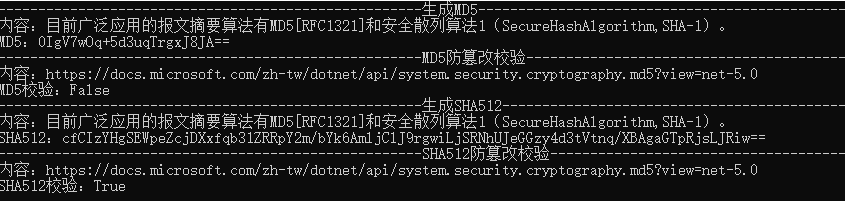
计算机网络安全 —— 报文摘要算法 MD5
一、报文摘要算法基本概念 使用加密通常可达到报文鉴别的目的,因为伪造的报文解密后一般不能得到可理解的内容。但简单采用这种方法,计算机很难自动识别报文是否被篡改。另外,对于不需要保密而只需要报文鉴别的网络应用,对整个…...

LeetCode 746. 使用最小花费爬楼梯 java题解
https://leetcode.cn/problems/min-cost-climbing-stairs/description/ 优化:可以不用dp数组,用变量,节省空间。 class Solution {public int minCostClimbingStairs(int[] cost) {int lencost.length;int[] dpnew int[len1];dp[0]0;//爬到0…...
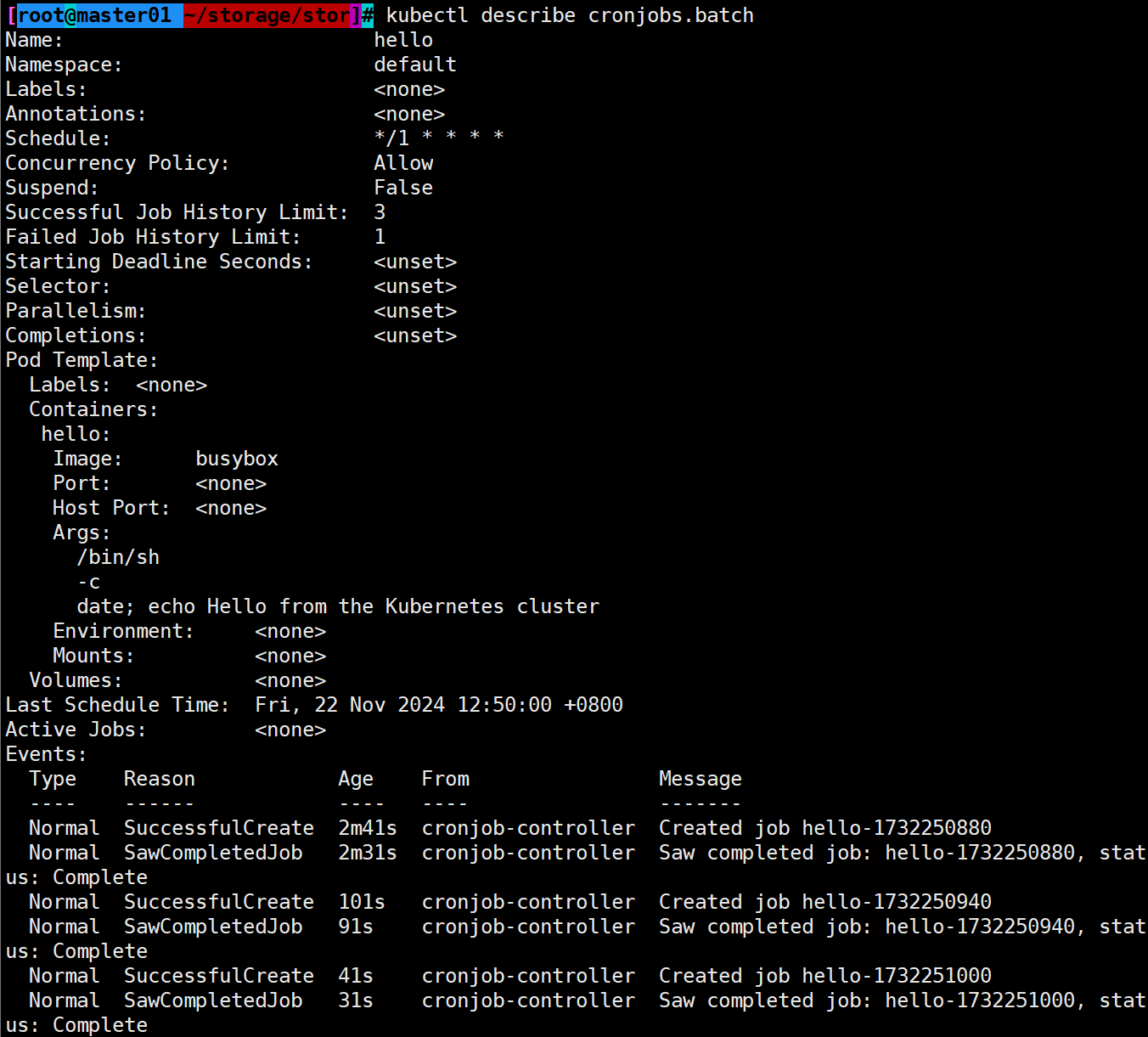
Kubernetes的pod控制器
文章目录 一,什么是pod控制器二,pod控制器类型(重点)1.ReplicaSet2.Deployment3.DaemonSet4.StatefulSet5.Job6.Cronjob 三,pod与控制器的关系1.Deployment2.SatefulSet2.1StatefulSet组成2.2headless的由来2.3有状态服…...

ArcMap 处理栅格数据地形图配准操作
ArcMap 处理栅格数据地形图配准操作今天分享 一、地形图配准 1、绘图 点击 开始绘制,四条线 2、地理配准 1)点击弹出 2)画控制点 关闭自动校正 画线 从焦点向外划线,然后邮件输入坐标弹出框,填写相应内容,…...

comprehension
1.读题---猜---文章主题 只读题目,不读选项 2.文章--定位 3.用文章对应选项 1 be based on be dependent upon 2 fruitful adj.富有成效的;硕果累累的; 3 unfruitful adj.徒然的,无益的,没有结果的 4 desperately adv.拼命地&#x…...

开源宝藏:Smart-Admin 重复提交防护的 AOP 切面实现详解
首先,说下重复提交问题,基本上解决方案,核心都是根据URL、参数、token等,有一个唯一值检验是否重复提交。 而下面这个是根据用户id,唯一值进行判定,使用两种缓存方式,redis和caffeineÿ…...

使用 npm 安装 Electron 作为开发依赖
好的,下面是一个使用 npm pack 和 npm install 命令来打包和安装离线版本的 npm 包的具体示例。我们将以 electron 为例,演示如何在有网络连接的机器上打包 electron,然后在没有网络连接的机器上安装它。 步骤 1: 在有网络连接的机器上打包 …...

JavaWeb之综合案例
前言 这一节讲一个案例 1. 环境搭建 然后就是把这些数据全部用到sql语句中执行 2.查询所有-后台&前台 我们先写后台代码 2.1 后台 2.2 Dao BrandMapper: 注意因为数据库里面的名称是下划线分割的,我们类里面是驼峰的,所以要映射 …...

MySQL 报错:1137 - Can‘t reopen table
MySQL 报错:1137 - Can’t reopen table 1. 问题 对临时表查询: select a.ts_code,a.tsnum,b.tsnum from (select t.ts_code ,count(*) tsnum from tmp_table t group by t.ts_code having count(*) > 20 and count(*)< 50 ) a ,(select t.ts_…...

Claude3.5-Sonnet和GPT-4o怎么选(附使用链接)
随着人工智能模型的不断进化,传统的评估标准已经逐渐变得陈旧和不再适用。以经典的“喝水测试”为例,过去广泛应用于检测模型能力,但现如今即便是国内的一些先进模型,也能够轻松答对这些简单的问题。因此,我们亟需引入…...

使用itextpdf进行pdf模版填充中文文本时部分字不显示问题
在网上找了很多种办法 都解决不了; 最后发现是文本域字体设置出了问题; 在这不展示其他的代码 只展示重要代码; 1 引入扩展包 <dependency><groupId>com.itextpdf</groupId><artifactId>itext-asian</artifactId><version>5.2.0</v…...

java-贪心算法
1. 霍夫曼编码(Huffman Coding) 描述: 霍夫曼编码是一种使用变长编码表对数据进行编码的算法,由David A. Huffman在1952年发明。它是一种贪心算法,用于数据压缩。霍夫曼编码通过构建一个二叉树(霍夫曼树&a…...

OpenCV和Qt坐标系不一致问题
“ OpenCV和QT坐标系导致绘图精度下降问题。” OpenCV和Qt常用的坐标系都是笛卡尔坐标系,但是细微处有些不同。 01 — OpenCV坐标系 OpenCV是图像处理库,是以图像像素为一个坐标位置,即一个像素对应一个坐标,所以其坐标系也叫图像…...

前端VUE项目启动方式
将VUE项目的前端项目运行起来,整个过程非常简单,预计5分钟就可以完成,取决于大家的网速。 项目运行先安装Node.js Windows 安装 Node.js 指南:http://www.iocoder.cn/NodeJS/windows-install(opens new window) Mac 安装 Node.js…...
)
Python小白学习教程从入门到入坑------习题课5(基础巩固)
目录 实战题 1、“千年虫”是什么虫? 2、模拟京东购物流程 3、模拟12306火车票订票流程 4、模拟手机通讯录 实战题 1、“千年虫”是什么虫? 要求:已知一个列表中存储的是员工的出生年份 [88,89,90,98,00,99] 由于时间比较久,出生的年份均为2位整数…...

飞凌嵌入式T113-i开发板RISC-V核的实时应用方案
随着市场对嵌入式设备的功能需求越来越高,集成了嵌入式处理器和实时处理器的主控方案日益增多,以便更好地平衡性能与效率——实时核负责高实时性任务,A核处理复杂任务,两核间需实时交换数据。然而在数据传输方面,传统串…...

基于Java后台实现百度、高德和WGS84坐标的转换实战
目录 前言 一、需求的缘由 1、百度坐标拾取 2、高德坐标拾取 3、不同地图的坐标展示 二、后端坐标偏移转换处理 1、相关类库介绍 2、coordtransorm类图介绍 3、后台实际转换 三、总结 前言 在当今数字化时代,地理位置信息的精确性和实时性对于各种应用至…...

SQL,力扣题目1635,Hopper 公司查询 I
一、力扣链接 LeetCode_1635 二、题目描述 表: Drivers ---------------------- | Column Name | Type | ---------------------- | driver_id | int | | join_date | date | ---------------------- driver_id 是该表的主键(具有唯一值的列)。 该表的每一行…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...

STL 2迭代器
文章目录 1.迭代器2.输入迭代器3.输出迭代器1.插入迭代器 4.前向迭代器5.双向迭代器6.随机访问迭代器7.不同容器返回的迭代器类型1.输入 / 输出迭代器2.前向迭代器3.双向迭代器4.随机访问迭代器5.特殊迭代器适配器6.为什么 unordered_set 只提供前向迭代器? 1.迭代器…...
