C++二级:满足条件的数的累加
现有n个整数,将其中个位数为k的数进行累加求和。
输入
第一行1个整数n。( 0 < n < 1000) 第二行n个非负整数,以空格分隔,每个数不大于100000。
第三行1个整数k。(0 ≤ k ≤ 9)
输出
输出满足题目要求的累加和。
样例输入
10
2 5 7 17 11 18 4 27 1 7
7
样例输出
58
#include <bits/stdc++.h>
using namespace std;
int main()
{int n,k,sum=0;int a[20];cin >> n;for(int i=0;i<n;i++){cin >> a[i];}cin >> k;for(int i=0;i<n;i++){if(a[i]%10==k) sum += a[i];}cout << sum;return 0;
} 相关文章:

C++二级:满足条件的数的累加
现有n个整数,将其中个位数为k的数进行累加求和。 输入 第一行1个整数n。( 0 < n < 1000) 第二行n个非负整数,以空格分隔,每个数不大于100000。 第三行1个整数k。(0 ≤ k ≤ 9) 输出 输出满足题目要求的累加和。…...

【山大909算法题】2014-T1
文章目录 1.原题2.算法思想3.关键代码4.完整代码5.运行结果 1.原题 为带表头的单链表类Chain编写一个成员函数Reverse,该函数对链表进行逆序操作(将链表中的结点按与原序相反的顺序连接),要求逆序操作就地进行,不分配…...

【MySQL实战45讲笔记】基础篇——深入浅出索引(上)
系列文章 基础篇——MySQL 的基础架构 基础篇——redo log 和 binlog 基础篇——事务隔离 目录 系列文章深入浅出索引(上)4.1 索引的常见模型4.2 InnoDB 的索引模型4.3 索引维护4.4 思考:为什么要重建索引以及如何做? 深入浅出索…...

通关C语言自定义类型:联合和枚举
C语言的自定义类型有四个分别是:数组;结构体(struct);联合体(union);枚举(enum)。前面已经讨论过数组和结构体,这期让我们来学习一下联合体和枚举…...
python高阶技巧一
闭包 简单认识一下闭包 以下代码,内层inner函数不仅依赖于自身的参数b,还依赖于外层outer函数的参数a。inner就是一个闭包函数,既能访问外部变量,又保证外部变量不是全局的,不会被篡改掉,确保了外部变量的…...

Java 对象头、Mark Word、monitor与synchronized关联关系以及synchronized锁优化
1. 对象在内存中的布局分为三块区域: (1)对象头(Mark Word、元数据指针和数组长度) 对象头:在32位虚拟机中,1个机器码等于4字节,也就是32bit,在64位虚拟机中࿰…...

鸿蒙网络编程系列50-仓颉版TCP回声服务器示例
1. TCP服务端简介 TCP服务端是基于TCP协议构建的一种网络服务模式,它为HTTP(超文本传输协议)、SMTP(简单邮件传输协议)等高层协议的应用程序提供了可靠的底层支持。在TCP服务端中,服务器启动后会监听一个或…...

软件测试基础(自动化测试、性能测试)
🍅 点击文末小卡片 ,免费获取软件测试全套资料,资料在手,涨薪更快 自动化测试的意义 缩短软件开发测试周期,可以让产品更快投放市场 测试效率高,充分利用硬件资源 节省人力资源,降低测试…...

C++中的原子操作:原子性、内存顺序、性能优化与原子变量赋值
一、原子操作与原子性 原子操作(atomic operation)是并发编程中的一个核心概念,指的是在多线程环境中,一个操作一旦开始,就不会被其他线程的操作打断,直至该操作完成。这种不可分割的特性保证了操作的原子…...

游戏引擎学习第19天
介绍 这段内容描述了开发者在进行游戏开发时,对于音频同步和平台层的理解和调整的过程。以下是更详细的复述: 开发者表达了他希望今天继续进行的工作内容。他提到,昨天他讲解了一些关于音频的内容,今天他想稍微深入讲解一下他正…...

RocketMQ: 专业术语以及相关问题解决
概述 要了解 RocketMQ 的多个关键特性的实现原理,并对消息中间件遇到的各种问题进行解决我们引用 JMS 规范 与 CORBA Notification 规范,规范为我们设计系统指明了方向但是仍有不少问题规范没有提及,对于消息中间件又至关重要RocketMQ 并不遵…...

C++ 类和对象中的 拷贝构造 和 运算符重载
构造函数中可以添加参数并添加默认值构成缺省构造,如果我们在构造函数的参数中加上自身类型类的引用和其他给出默认值的参数则会构成一种特殊的构造函数叫做———拷贝构造函数 1.拷贝构造 拷贝构造的特点: 1.拷贝构造函数是构造函数的一个重载 2.拷…...

el-table最大高度无法滚动
解决el-table同时使用fixed和计算的最大高度时固定右边的列无法跟随滚动的问题 原因:el-table组件会根据传入的 max-height 计算表格内容部分 和 fixed部分的最大高度,以此来生成滚动条和产生滚动效果,当传入的 max-height 为一个计算的高度…...

Vscode写markdown快速插入python代码
如图当我按下快捷键CRTLSHIFTK 自动出现python代码片段 配置方法shortcuts’ 打开这个json文件 输入 {"key": "ctrlshiftk","command": "editor.action.insertSnippet","when": "editorTextFocus","args&…...

基于 NCD 与优化函数结合的非线性优化 PID 控制
基于 NCD 与优化函数结合的非线性优化 PID 控制 1. 引言 NCD(Normalized Coprime Factorization Distance)优化是一种用于非线性系统的先进控制方法。通过将 NCD 指标与优化算法结合,可以在动态调整控制参数的同时优化控制器性能。此方法特别…...

【数据分析】基于GEE实现大津算法提取洞庭湖流域水体
大津算法提取水体 1.写在前面2.洞庭湖水体识别1.写在前面 最大类间方差法,也称为Otsu或大津法,是一种高效的图像二值化算法,由日本学者Otsu于1979年提出。该算法基于图像的频率分布直方图,假设图像包含两类像素(前景和背景),并计算出一个最佳阈值,以最大化类间方差,从…...
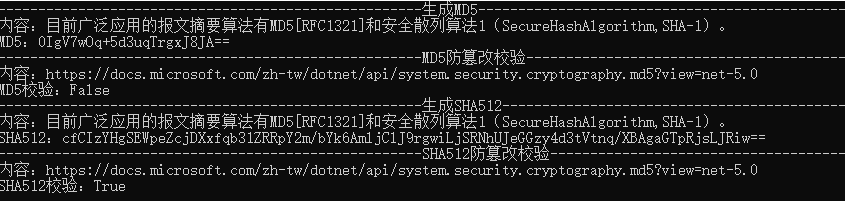
计算机网络安全 —— 报文摘要算法 MD5
一、报文摘要算法基本概念 使用加密通常可达到报文鉴别的目的,因为伪造的报文解密后一般不能得到可理解的内容。但简单采用这种方法,计算机很难自动识别报文是否被篡改。另外,对于不需要保密而只需要报文鉴别的网络应用,对整个…...

LeetCode 746. 使用最小花费爬楼梯 java题解
https://leetcode.cn/problems/min-cost-climbing-stairs/description/ 优化:可以不用dp数组,用变量,节省空间。 class Solution {public int minCostClimbingStairs(int[] cost) {int lencost.length;int[] dpnew int[len1];dp[0]0;//爬到0…...
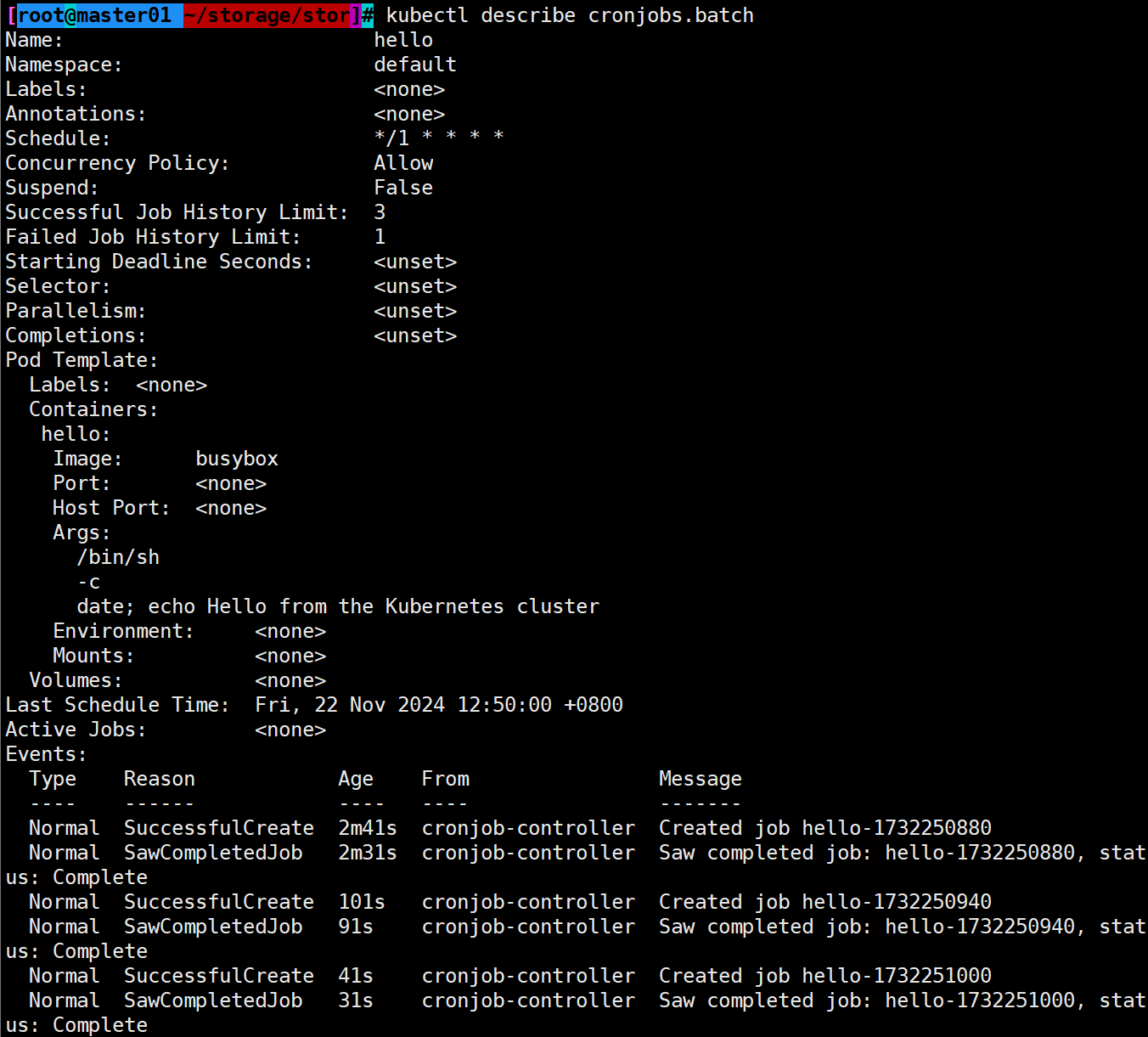
Kubernetes的pod控制器
文章目录 一,什么是pod控制器二,pod控制器类型(重点)1.ReplicaSet2.Deployment3.DaemonSet4.StatefulSet5.Job6.Cronjob 三,pod与控制器的关系1.Deployment2.SatefulSet2.1StatefulSet组成2.2headless的由来2.3有状态服…...

ArcMap 处理栅格数据地形图配准操作
ArcMap 处理栅格数据地形图配准操作今天分享 一、地形图配准 1、绘图 点击 开始绘制,四条线 2、地理配准 1)点击弹出 2)画控制点 关闭自动校正 画线 从焦点向外划线,然后邮件输入坐标弹出框,填写相应内容,…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
