【通俗理解】隐变量的变分分布探索——从公式到应用
【通俗理解】隐变量的变分分布探索——从公式到应用
关键词提炼
#隐变量 #变分分布 #概率模型 #公式推导 #期望最大化 #机器学习 #变分贝叶斯 #隐马尔可夫模型
第一节:隐变量的变分分布的类比与核心概念【尽可能通俗】
隐变量的变分分布就像是一场“捉迷藏”游戏,在这场游戏中,我们试图通过观察到的线索(即观测数据)来推测那些隐藏起来的小伙伴(即隐变量)的位置和状态。
而变分分布,就是我们在这场游戏中,根据已有线索和假设,对隐变量可能状态的猜测和描述。
第二节:隐变量的变分分布的核心概念与应用
2.1 核心概念
| 核心概念 | 定义 | 比喻或解释 |
|---|---|---|
| 隐变量Z | 在概率模型中,无法直接观测到的变量,但影响观测数据X的分布。 | 像是藏在盒子里的神秘礼物,我们看不到它,但能感受到它的存在。 |
| 变分分布q(Z) | 对隐变量Z的分布进行的一种估计或猜测,用于近似真实的后验分布p(Z|X)。 | 像是我们根据线索,对隐变量位置的一种猜测和描述。 |
| 期望最大化(EM) | 一种迭代算法,用于在存在隐变量的情况下,估计模型参数。 | 像是我们通过不断调整猜测,来逐渐接近隐变量的真实状态。 |
2.2 优势与劣势
| 方面 | 描述 |
|---|---|
| 优势 | 能够处理含有隐变量的复杂概率模型,提供对隐变量分布的估计,进而用于模型推断和预测。 |
| 劣势 | 变分分布的准确性依赖于模型的假设和观测数据的充分性,可能存在估计偏差。 |
2.3 与机器学习的类比
隐变量的变分分布在机器学习中扮演着“侦探”的角色,它通过分析观测数据中的线索,来推测那些隐藏在背后的变量和状态,为模型的推断和预测提供有力支持。
第三节:公式探索与推演运算【重点在推导】
3.1 基本公式
在变分贝叶斯方法中,我们常用KL散度来衡量变分分布q(Z)与真实后验分布p(Z|X)之间的差异,并试图最小化这个差异:
KL ( q ( Z ) ∥ p ( Z ∣ X ) ) = E q ( Z ) [ log q ( Z ) − log p ( Z ∣ X ) ] \text{KL}(q(Z) \| p(Z|X)) = \mathbb{E}_{q(Z)}[\log q(Z) - \log p(Z|X)] KL(q(Z)∥p(Z∣X))=Eq(Z)[logq(Z)−logp(Z∣X)]
由于p(Z|X)难以直接计算,我们通常通过最大化证据下界(ELBO)来间接优化KL散度:
ELBO = E q ( Z ) [ log p ( X , Z ) − log q ( Z ) ] \text{ELBO} = \mathbb{E}_{q(Z)}[\log p(X, Z) - \log q(Z)] ELBO=Eq(Z)[logp(X,Z)−logq(Z)]
3.2 具体实例与推演
考虑一个简单的隐马尔可夫模型,其中隐变量Z表示状态序列,观测数据X表示对应的观测序列。我们可以使用变分贝叶斯方法来估计隐变量的分布。
假设我们有以下公式:
- 观测数据的似然函数: p ( X ∣ Z ) p(X|Z) p(X∣Z)
- 隐变量的先验分布: p ( Z ) p(Z) p(Z)
- 变分分布: q ( Z ) q(Z) q(Z)(通常选择为易于处理的分布,如高斯分布)
我们的目标是最大化ELBO:
ELBO = E q ( Z ) [ log p ( X , Z ) − log q ( Z ) ] \text{ELBO} = \mathbb{E}_{q(Z)}[\log p(X, Z) - \log q(Z)] ELBO=Eq(Z)[logp(X,Z)−logq(Z)]
通过展开和化简,我们可以得到具体的优化目标,并通过梯度上升等算法来求解。
第四节:相似公式比对【重点在差异】
| 公式/模型 | 共同点 | 不同点 |
|---|---|---|
| 期望最大化(EM) | 都用于处理含有隐变量的模型参数估计。 | EM算法通过迭代求解期望步和最大化步来优化参数,而变分贝叶斯方法则通过优化变分分布来近似后验分布。 |
| 变分自编码器(VAE) | 都涉及到了变分分布的概念。 | VAE是一种生成模型,用于数据的生成和重构,而变分贝叶斯方法更侧重于模型推断和隐变量分布的估计。 |
第五节:核心代码与可视化【全英文的代码,标签label尤其需要是英文的!】
以下是一个使用变分贝叶斯方法进行隐变量估计的简化示例代码(假设已定义好相关函数和模型):
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.optimize import minimize# Define the log joint probability log p(X, Z)
def log_joint_probability(Z, X, model_params):# ... (implementation details)return log_p_XZ# Define the log variational distribution log q(Z)
def log_q(Z, variational_params):# ... (implementation details)return log_q_Z# Define the Evidence Lower Bound (ELBO) to maximize
def elbo(variational_params, X, model_params):# Sample from the variational distributionZ_samples = np.random.normal(loc=variational_params['mu'], scale=np.sqrt(variational_params['sigma']), size=(num_samples,))# Calculate the ELBOlog_p_XZ_samples = np.array([log_joint_probability(z, X, model_params) for z in Z_samples])log_q_Z_samples = np.array([log_q(z, variational_params) for z in Z_samples])elbo_value = np.mean(log_p_XZ_samples - log_q_Z_samples)return -elbo_value # We need to minimize the negative ELBO# Initialize variational parameters
variational_params = {'mu': 0.0, 'sigma': 1.0}# Optimize the variational parameters to maximize the ELBO
result = minimize(elbo, variational_params, args=(X, model_params), method='L-BFGS-B')# Extract optimized parameters
optimized_mu = result.x[0]
optimized_sigma = np.exp(result.x[1]) # Ensure sigma is positive# Visualize the results
sns.set_theme(style="whitegrid")
plt.hist(Z_samples, bins=30, density=True, alpha=0.6, color='g', label='Variational Distribution q(Z)')
plt.axvline(optimized_mu, color='r', linestyle='dashed', linewidth=2, label=f'Optimized mu: {optimized_mu:.2f}')
plt.xlabel('Hidden Variable Z')
plt.ylabel('Density')
plt.title('Variational Distribution of Hidden Variable Z')
plt.legend()
plt.show()print(f"Optimized variational parameters: mu = {optimized_mu:.2f}, sigma = {optimized_sigma:.2f}")
| 输出内容 | 描述 |
|---|---|
| 变分分布的直方图 | 显示了优化后的变分分布q(Z)的形状。 |
| 优化后的变分参数 | 提供了变分分布q(Z)的均值和标准差。 |
| 图表标题、x轴标签、y轴标签 | 提供了图表的基本信息和说明。 |
参考文献
- Blei, D. M., Kucukelbir, A., & McAuliffe, J. D. (2017). Variational inference: A review for statisticians. Journal of the American Statistical Association, 112(518), 859-877. [【影响因子=4.0,统计学领域权威期刊】]内容概述:该论文对变分推断方法进行了全面回顾,介绍了其在统计学中的应用和优势,为理解和使用变分分布提供了理论基础。
- Kingma, D. P., & Welling, M. (2014). Auto-encoding variational bayes. In International Conference on Learning Representations. [【会议论文,机器学习领域重要会议】]内容概述:该论文提出了变分自编码器(VAE)模型,通过变分推断方法来学习数据的生成过程,为变分分布在生成模型中的应用提供了重要思路。
相关文章:

【通俗理解】隐变量的变分分布探索——从公式到应用
【通俗理解】隐变量的变分分布探索——从公式到应用 关键词提炼 #隐变量 #变分分布 #概率模型 #公式推导 #期望最大化 #机器学习 #变分贝叶斯 #隐马尔可夫模型 第一节:隐变量的变分分布的类比与核心概念【尽可能通俗】 隐变量的变分分布就像是一场“捉迷藏”游戏…...

PyTorch 分布式并行计算
0. Abstract 使用 PyTorch 进行多卡训练, 最简单的是 DataParallel, 仅仅添加一两行代码就可以使模型在多张 GPU 上并行地计算. 但它是比较老的方法, 官方推荐使用新的 Distributed Data Parallel, 更加灵活与强大: 1. Distributed Data Parallel (DDP) 从一个简单的非分布…...
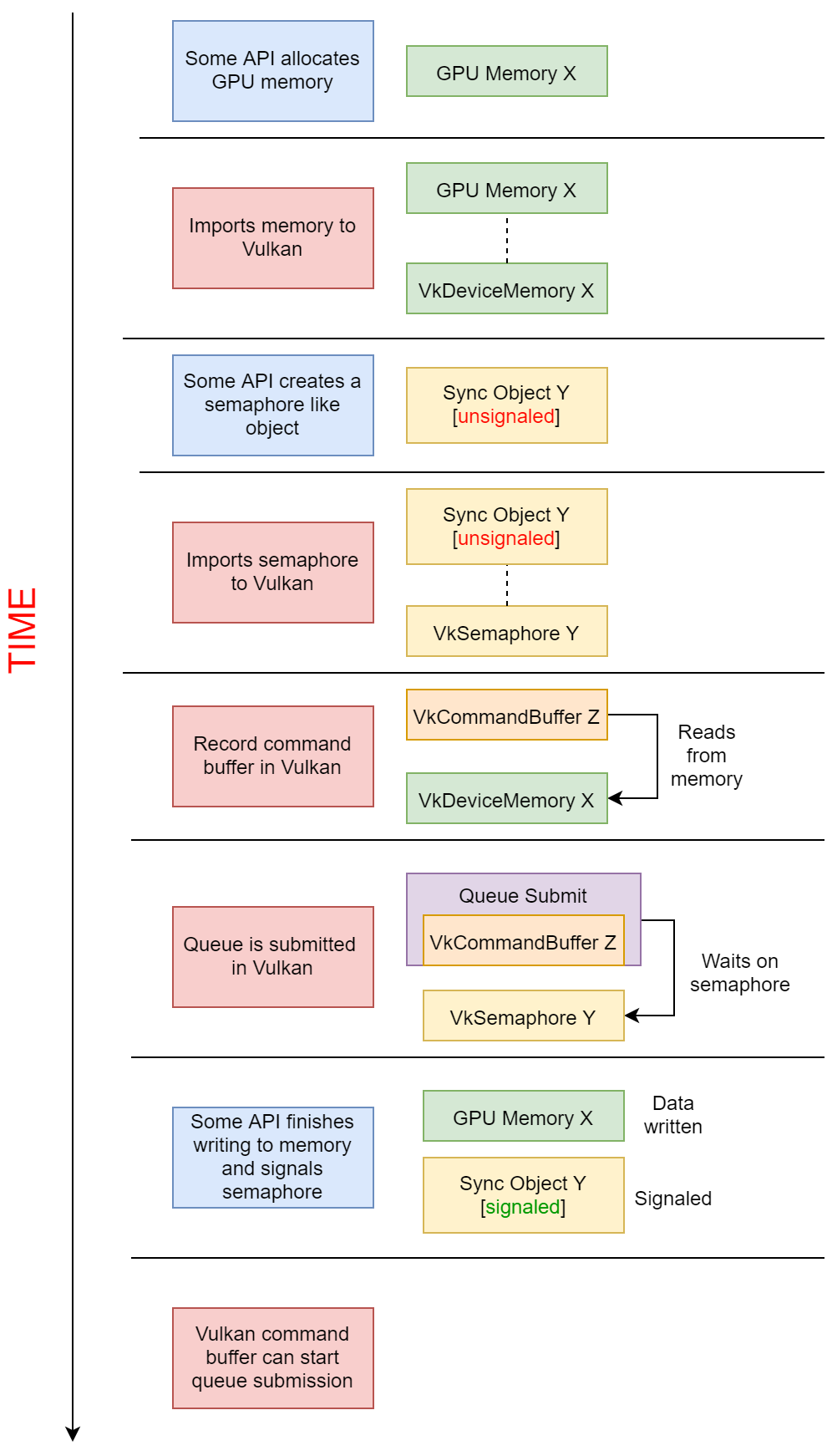
[cg] vulkan external_memory
最近在写硬件编码的代码,渲染器渲染出的RT需要给到编码器做硬编,有两种方法能做。 一是通过 map的方式,把显存里的数据读到cpu,拷贝一份cpu data给编码器,但这种方式会有内存拷贝的开销。所以,我们思考是否…...

如何使用Python代码实现给GPU预加热
如何使用Python代码实现给GPU预加热 一、引言二、使用深度学习框架进行预加热2.1 TensorFlow预加热2.2 PyTorch预加热三、使用CUDA进行预加热四、预加热的效果评估与优化五、结论与展望在高性能计算和深度学习领域,GPU(图形处理器)已经成为不可或缺的加速工具。然而,在实际…...

硬件知识 cadence16.6 原理图输出为pdf 网络名下划线偏移 (ORCAD)
1. cadence原理图输出为PDF网络名下划线偏移 生这种情况的原因 1. 设计的原理图图纸大小比正常的 A4图纸大。 2. 打印为PDF 的时候,打印机的设置有问题。 2.cadence原理图输出为 PDF网络名下划线偏移的情况 可以看到上图,网络名往上漂移。 3. 解决办法 …...

ffmpeg视频滤镜:提取缩略图-framestep
滤镜描述 官网地址 > FFmpeg Filters Documentation 这个滤镜会间隔N帧抽取一帧图片,因此这个可以用于设置视频的缩略图。总体上这个滤镜比较简单。 滤镜使用 滤镜参数 framestep AVOptions:step <int> ..FV....... set frame st…...
RecyclerView详解——(四)缓存复用机制
稍微看了下源码和部分文章,在此做个小小的总结 RecyclerView,意思为可回收的view,那么相对于listview,他的缓存复用肯定是一大优化。 具体而言,当一个列表项被移出屏幕后,RecyclerView并不会销毁其视图&a…...

进程 系统调用 中断
进程P通过执行系统调用从键盘接收一个字符的输入,已知此过程中与进程P相关的操作包括: ①将进程P插入就绪队列; ②将进程P插入阻塞队列; ③将字符从键盘控制器读入系统缓冲区; ④启动键盘中断处理程序; …...
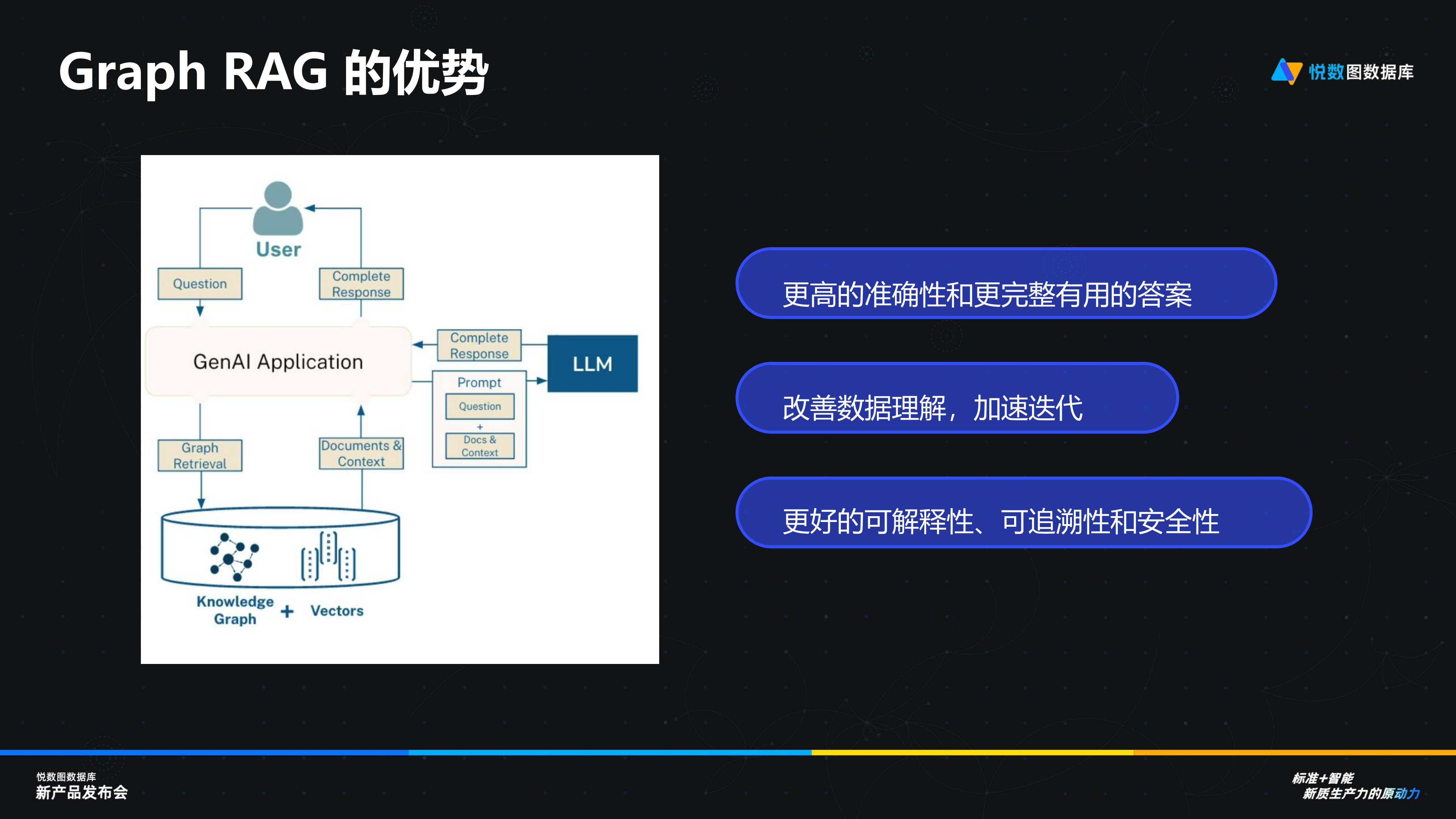
演讲回顾丨杭州悦数 CTO 叶小萌:图数据库发展新航向——拥抱 GQL,融合 HTAP,携手 AI
本文为杭州悦数 CTO 叶小萌在“标准智能:新质生产力的原动力”悦数图数据库新产品发布会上的演讲回顾,主题为:《新标准、新期待:展望图数据库发展的关键方向》 各位嘉宾、悦数图数据库的用户以及线上的观众朋友们大家好࿰…...

Java安全—JNDI注入RMI服务LDAP服务JDK绕过
前言 上次讲到JNDI注入这个玩意,但是没有细讲,现在就给它详细地讲个明白。 JNDI注入 那什么是JNDI注入呢,JNDI全称为 Java Naming and Directory Interface(Java命名和目录接口),是一组应用程序接口&…...

C++:设计模式-单例模式
单例模式(Singleton Pattern)是一种设计模式,确保一个类只有一个实例,并且提供全局访问点。实现单例模式的关键是防止类被多次实例化,且能够保证实例的唯一性。常见的实现手法包括懒汉式、饿汉式、线程安全的懒汉式等。…...

Softing工业将OPC UA信息建模集成到边缘应用和安全集成服务器中
Softing工业宣布将OPC UA(统一架构)信息建模集成到其边缘产品系列及安全集成服务器(SIS)中,这一技术进步使得在工业物联网(IIoT)应用中的数据集成、交换与控制更加无缝、有效。 (OPC…...

WPF中如何让Textbox显示为一条直线
由于Textbox直接使用是一条直线 设置如下代码 可以让Textbox变为直线输入 <Style TargetType"TextBox"x:Key"UsernameTextBoxStyle"><Setter Property"Template"><Setter.Value><ControlTemplate TargetType"{x:Typ…...

VSCode汉化教程【简洁易懂】
我们安装完成后默认是英文界面。 找到插件选项卡,搜索“Chinese”,找到简体(更具你的需要)(Microsoft提供)Install。 安装完成后选择Change Language and Restart。...

跨平台多开账号防关联:轻松管理多个账号!
对于跨境电商、独立站以及社媒营销领域,如何高效管理多个账号、确保账号安全是企业面临的重大挑战。那么如何仅用一台电脑就能实现跨平台多开账号呢? 一、为什么需要跨平台多开账号并防关联? 1. 品牌推广:不同平台拥有不同的用户…...

DICOM图像处理:深入解析DICOM彩色图像中的Planar配置及其对像素数据解析处理的实现
引言 在DICOM(Digital Imaging and Communications in Medicine)标准中,彩色图像的存储与显示涉及多个关键属性,其中**Planar Configuration(平面配置)**属性(标签 (0028,0006))尤为重要。当遇到彩色DICOM图像在浏览时被错误地分割为9张小图,而实际应显示为一…...

jupyter notebook的 markdown相关技巧
目录 1 先选择为markdown类型 2 开关技巧 2.1 运行markdown 2.2 退出markdown显示效果 2.3 注意点:一定要 先选择为markdown类型 3 一些设置技巧 3.1 数学公式 3.2 制表 3.3 目录和列表 3.4 设置各种字体效果:加粗,斜体&#x…...

Linux连接网络的三种方式
Linux 连接网络的三种常见方式如下: 桥接模式 原理:虚拟网络接口与物理网络接口或另一个虚拟接口 “桥接”,形成逻辑上的网络交换机,使所有通过该桥接设备的数据包能被转发到桥接组中的所有接口,如同在一个局域网内…...

##继承##
继承的概念 #继承是新模板基于老模板的基础上修改而成,制作新模板时不需要重新开始制作,可以在老模板的基础上进行修改.(如手机版本的换代,软件的版本更新等) #程序也可以继承 继承的格式: class 继承模块(被继承模块ÿ…...
)
2024 APMCM亚太数学建模C题 - 宠物行业及相关产业的发展分析和策略 完整参考论文(1)
摘要 近年来,中国宠物食品行业迅速增长,但面临复杂的国际形势和多变的市场环境,因此科学地分析和预测该行业的发展趋势至关重要。本研究通过构建多个机器学习与统计回归模型,量化分析中国宠物食品行业的关键驱动因素,预测未来宠物食品总产值和出口值。 在数据处理部分,…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
