算法中常用到的数学知识:埃拉托色尼筛法(获取质数)、欧几里得算法(求两个数最大公因数)
不管是在项目中还是面试时,一定的算法能力都是极其重要的。大多数算法只要有一定的基础,给足够的时间是可以写出来的,然而有一类算法,说难也不难,说简单也不简单,这种算法通常涉及到某种数学知识,如果了解这种知识那写出来就是易如反掌,而没了解过相应知识的就只能使用暴力解法,数据稍微多一点就超时,甚至暴力都写不出来。本文就给大家讲解一下两种相关的数学知识。
1.埃拉托色尼筛法
适用场景:
获取一段数字中所有的质数。
基本步骤:
1.创建一个列表:首先,创建一个从2开始到你想要检查的数n(包括n)的连续整数列表。
2.标记第一个数:从列表中的第一个数2开始,因为它是第一个质数。
3.划除倍数:从2的下一个数开始,标记2的所有倍数。因为这些数都可以被2整除,所以它们不是质数。
4.移动到下一个未标记的数:在列表中找到下一个未被划除的数,这个数就是下一个质数。对于这个新的质数,重复步骤3,划除它的所有倍数。
5.重复步骤:继续这个过程,每次都找到下一个未被划除的数,并划除它的所有倍数,直到你处理完所有小于或等于√n的数。因为一个数必须有一个因数小于或等于它的算数平方根。
6.剩余的数:列表中未被划除的数就是质数。
7.结束:当处理完所有小于或等于√n的数后,列表中剩余的未被划除的数就是范围内的质数。
基本代码:
//本段代码是我自己写的,不一定标准,有需要的同学可以自己查标准的写法。
let arr=[]
for(let i=2;i<=100;i++){//模拟一个2到100的数组arr.push(i)
}
let l=0,r=Math.ceil(Math.pow(arr[arr.length-1],1/2))//l为第一个质数的索引,r为最后一个数开方向上取整
while(arr[l]<=r){//外层循环从第一个数到最后一个数的开方向上取整for(let i=l+1;i<arr.length;i++){//内层循环是整个数组if(arr[i]%arr[l]===0){//判断该数能否整除第一个质数,能的话就从数组中删除,并且索引减一(因为for循环后面有一个加一,删除后不减一就会跳过一个数字)arr.splice(i,1)i--}}l++//内循环结束后第一个质数后移一位
}
console.log(arr)打印结果为[2,100]内所有质数

说明:
大家看到这应该会有很多疑问,比如:如果开头不是2怎么办,开头不是质数怎么办等等。我的理解只能将数组左侧扩充到2,然后在判断过程中加上对原来范围的控制,因为寻找质数的暴力方法只能是从2开始一个一个相除,所以该方法在寻找范围内所有质数在时间复杂度上已经有了很大的提升。
2.欧几里得算法,又名辗转相除法
适用场景:
求两个数最大公因数
基本步骤:
1.寻找两个数的较大数。
2.使用较大数除以较小数,再使用本次计算中的除数除以余数
3.重复步骤2,当余数为0时,本次计算的除数就是两个数最大公约数。
基本代码:
let a=12,b=18//任意定义两个数,为了方便所以定义的比较小,c为计算过程中的余数
if(b>a)[a,b]=[b,a]//保证a是较大数
while(1){//死循环,因为最大公因数一定有值,最小也是1let c=a%bif(c===0){//当余数为0就跳出循环,否则修改a和b的值,继续循环break}a=bb=c
}
console.log(b)//最后一次计算的除数就是最大公因数:6相关文章:

算法中常用到的数学知识:埃拉托色尼筛法(获取质数)、欧几里得算法(求两个数最大公因数)
不管是在项目中还是面试时,一定的算法能力都是极其重要的。大多数算法只要有一定的基础,给足够的时间是可以写出来的,然而有一类算法,说难也不难,说简单也不简单,这种算法通常涉及到某种数学知识࿰…...

实战OpenCV之人脸识别
基础入门 随着计算机视觉技术和深度学习的发展,人脸识别已经成为一项广泛应用的技术,涵盖了从安全监控、身份验证、智能家居到大型公共安全项目等多个领域。 人脸识别技术通常包括以下几个主要步骤。 图像采集:通过摄像头或其他图像采集设备,捕获包含人脸的图像或视频帧。 …...

图像预处理之图像滤波
目录 图像滤波概览 均值滤波(Mean Filter) 中值滤波(Median Filter) 高斯滤波(Gaussian Filter) 双边滤波(Bilateral Filter) 方框滤波(Box Filter) S…...

【通俗理解】隐变量的变分分布探索——从公式到应用
【通俗理解】隐变量的变分分布探索——从公式到应用 关键词提炼 #隐变量 #变分分布 #概率模型 #公式推导 #期望最大化 #机器学习 #变分贝叶斯 #隐马尔可夫模型 第一节:隐变量的变分分布的类比与核心概念【尽可能通俗】 隐变量的变分分布就像是一场“捉迷藏”游戏…...

PyTorch 分布式并行计算
0. Abstract 使用 PyTorch 进行多卡训练, 最简单的是 DataParallel, 仅仅添加一两行代码就可以使模型在多张 GPU 上并行地计算. 但它是比较老的方法, 官方推荐使用新的 Distributed Data Parallel, 更加灵活与强大: 1. Distributed Data Parallel (DDP) 从一个简单的非分布…...
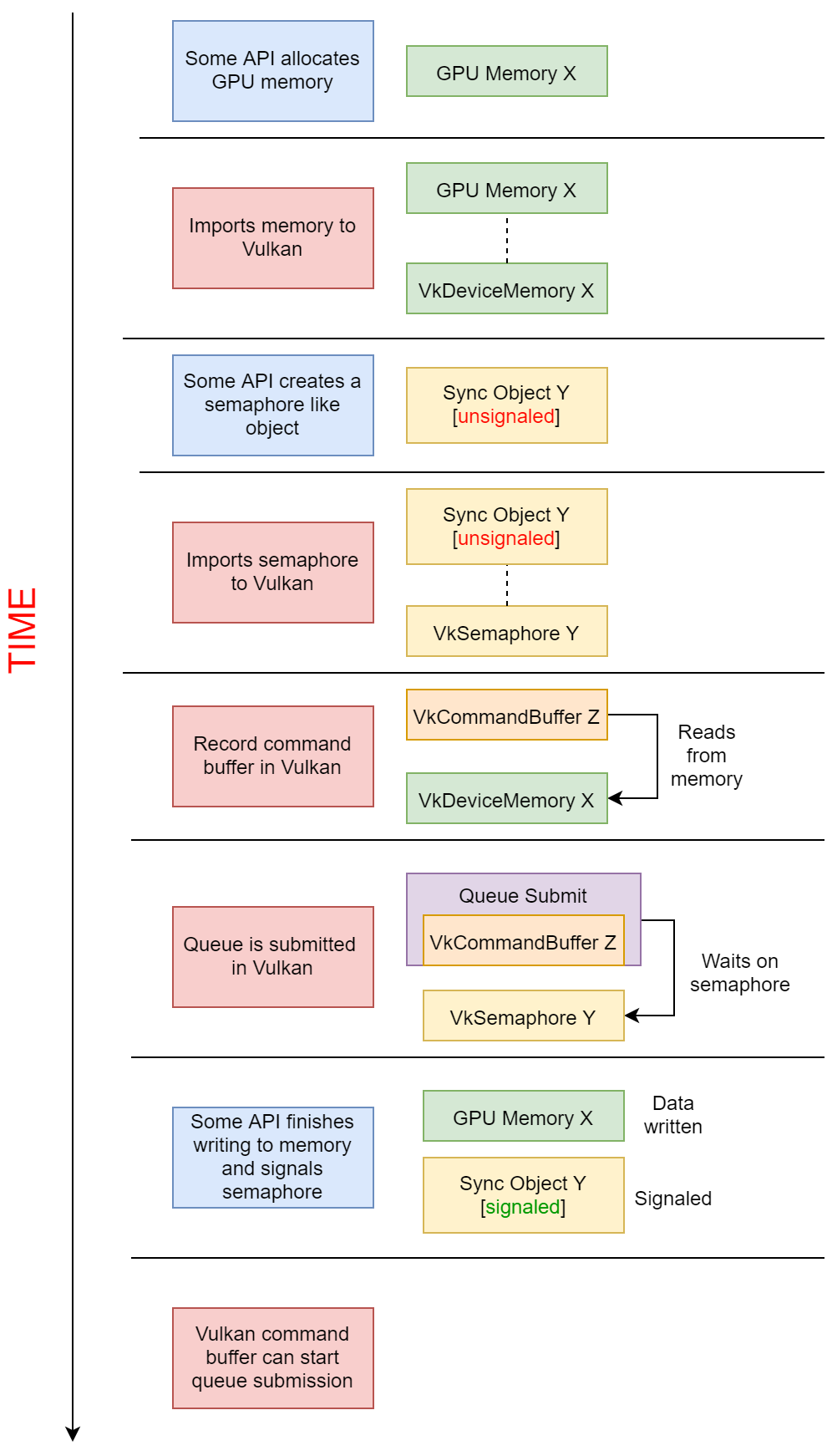
[cg] vulkan external_memory
最近在写硬件编码的代码,渲染器渲染出的RT需要给到编码器做硬编,有两种方法能做。 一是通过 map的方式,把显存里的数据读到cpu,拷贝一份cpu data给编码器,但这种方式会有内存拷贝的开销。所以,我们思考是否…...

如何使用Python代码实现给GPU预加热
如何使用Python代码实现给GPU预加热 一、引言二、使用深度学习框架进行预加热2.1 TensorFlow预加热2.2 PyTorch预加热三、使用CUDA进行预加热四、预加热的效果评估与优化五、结论与展望在高性能计算和深度学习领域,GPU(图形处理器)已经成为不可或缺的加速工具。然而,在实际…...

硬件知识 cadence16.6 原理图输出为pdf 网络名下划线偏移 (ORCAD)
1. cadence原理图输出为PDF网络名下划线偏移 生这种情况的原因 1. 设计的原理图图纸大小比正常的 A4图纸大。 2. 打印为PDF 的时候,打印机的设置有问题。 2.cadence原理图输出为 PDF网络名下划线偏移的情况 可以看到上图,网络名往上漂移。 3. 解决办法 …...

ffmpeg视频滤镜:提取缩略图-framestep
滤镜描述 官网地址 > FFmpeg Filters Documentation 这个滤镜会间隔N帧抽取一帧图片,因此这个可以用于设置视频的缩略图。总体上这个滤镜比较简单。 滤镜使用 滤镜参数 framestep AVOptions:step <int> ..FV....... set frame st…...
RecyclerView详解——(四)缓存复用机制
稍微看了下源码和部分文章,在此做个小小的总结 RecyclerView,意思为可回收的view,那么相对于listview,他的缓存复用肯定是一大优化。 具体而言,当一个列表项被移出屏幕后,RecyclerView并不会销毁其视图&a…...

进程 系统调用 中断
进程P通过执行系统调用从键盘接收一个字符的输入,已知此过程中与进程P相关的操作包括: ①将进程P插入就绪队列; ②将进程P插入阻塞队列; ③将字符从键盘控制器读入系统缓冲区; ④启动键盘中断处理程序; …...
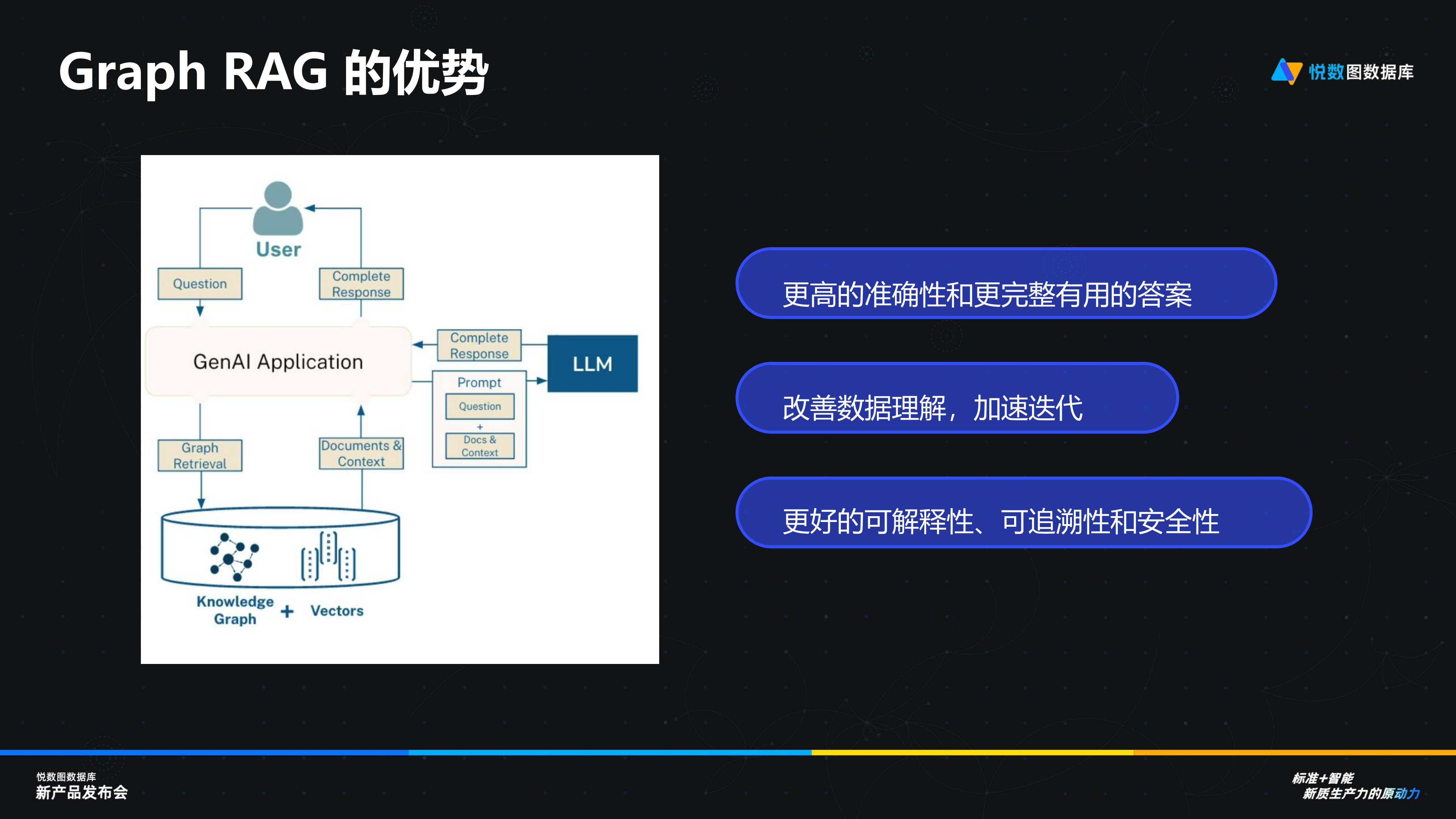
演讲回顾丨杭州悦数 CTO 叶小萌:图数据库发展新航向——拥抱 GQL,融合 HTAP,携手 AI
本文为杭州悦数 CTO 叶小萌在“标准智能:新质生产力的原动力”悦数图数据库新产品发布会上的演讲回顾,主题为:《新标准、新期待:展望图数据库发展的关键方向》 各位嘉宾、悦数图数据库的用户以及线上的观众朋友们大家好࿰…...

Java安全—JNDI注入RMI服务LDAP服务JDK绕过
前言 上次讲到JNDI注入这个玩意,但是没有细讲,现在就给它详细地讲个明白。 JNDI注入 那什么是JNDI注入呢,JNDI全称为 Java Naming and Directory Interface(Java命名和目录接口),是一组应用程序接口&…...

C++:设计模式-单例模式
单例模式(Singleton Pattern)是一种设计模式,确保一个类只有一个实例,并且提供全局访问点。实现单例模式的关键是防止类被多次实例化,且能够保证实例的唯一性。常见的实现手法包括懒汉式、饿汉式、线程安全的懒汉式等。…...

Softing工业将OPC UA信息建模集成到边缘应用和安全集成服务器中
Softing工业宣布将OPC UA(统一架构)信息建模集成到其边缘产品系列及安全集成服务器(SIS)中,这一技术进步使得在工业物联网(IIoT)应用中的数据集成、交换与控制更加无缝、有效。 (OPC…...

WPF中如何让Textbox显示为一条直线
由于Textbox直接使用是一条直线 设置如下代码 可以让Textbox变为直线输入 <Style TargetType"TextBox"x:Key"UsernameTextBoxStyle"><Setter Property"Template"><Setter.Value><ControlTemplate TargetType"{x:Typ…...

VSCode汉化教程【简洁易懂】
我们安装完成后默认是英文界面。 找到插件选项卡,搜索“Chinese”,找到简体(更具你的需要)(Microsoft提供)Install。 安装完成后选择Change Language and Restart。...

跨平台多开账号防关联:轻松管理多个账号!
对于跨境电商、独立站以及社媒营销领域,如何高效管理多个账号、确保账号安全是企业面临的重大挑战。那么如何仅用一台电脑就能实现跨平台多开账号呢? 一、为什么需要跨平台多开账号并防关联? 1. 品牌推广:不同平台拥有不同的用户…...

DICOM图像处理:深入解析DICOM彩色图像中的Planar配置及其对像素数据解析处理的实现
引言 在DICOM(Digital Imaging and Communications in Medicine)标准中,彩色图像的存储与显示涉及多个关键属性,其中**Planar Configuration(平面配置)**属性(标签 (0028,0006))尤为重要。当遇到彩色DICOM图像在浏览时被错误地分割为9张小图,而实际应显示为一…...

jupyter notebook的 markdown相关技巧
目录 1 先选择为markdown类型 2 开关技巧 2.1 运行markdown 2.2 退出markdown显示效果 2.3 注意点:一定要 先选择为markdown类型 3 一些设置技巧 3.1 数学公式 3.2 制表 3.3 目录和列表 3.4 设置各种字体效果:加粗,斜体&#x…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
