最多可收集的水果数目
三个小朋友收集水果问题:最大水果收集路径
问题描述
有一个游戏,游戏由 n x n 个房间网格状排布组成。给定一个大小为 n x n 的二维整数数组 fruits,其中 fruits[i][j] 表示房间 (i, j) 中的水果数目。
游戏开始时,三个小朋友分别从角落房间 (0, 0),(0, n - 1) 和 (n - 1, 0) 出发。每个小朋友都会恰好移动 n - 1 次,并到达房间 (n - 1, n - 1)。不同小朋友的移动规则如下:
- 第一个小朋友 从
(0, 0)出发,每次可以选择移动到(i + 1, j + 1)、(i + 1, j)或(i, j + 1)(如果存在)。 - 第二个小朋友 从
(0, n - 1)出发,每次可以选择移动到(i + 1, j - 1)、(i + 1, j)或(i + 1, j + 1)(如果存在)。 - 第三个小朋友 从
(n - 1, 0)出发,每次可以选择移动到(i - 1, j + 1)、(i, j + 1)或(i + 1, j + 1)(如果存在)。
每个小朋友到达一个房间时会收集该房间的所有水果。如果两个或更多小朋友进入同一个房间,则只有一个小朋友能收集该房间的水果,且该房间中的水果在收集后消失。
请你返回三个小朋友总共最多可以收集多少个水果。
示例
示例 1:
输入:
fruits = [[1, 2, 3, 4], [5, 6, 8, 7], [9, 10, 11, 12], [13, 14, 15, 16]]
输出:
100
解释:
第 1 个小朋友(绿色)的移动路径为 (0,0) -> (1,1) -> (2,2) -> (3, 3)。
第 2 个小朋友(红色)的移动路径为 (0,3) -> (1,2) -> (2,3) -> (3, 3)。
第 3 个小朋友(蓝色)的移动路径为 (3,0) -> (3,1) -> (3,2) -> (3,3)。
他们总共能收集 1 + 6 + 11 + 1 + 4 + 8 + 12 + 13 + 14 + 15 = 100 个水果。

示例 2:
输入:
fruits = [[1, 1], [1, 1]]
输出:
4
解释:
第 1 个小朋友的移动路径为 (0,0) -> (1,1)。
第 2 个小朋友的移动路径为 (0,1) -> (1,1)。
第 3 个小朋友的移动路径为 (1,0) -> (1,1)。
他们总共能收集 1 + 1 + 1 + 1 = 4 个水果。
思路分析
- 了解移动规则
第一个小朋友的路径是沿对角线移动的。因为每个格子只能被收集一次,第二个小朋友的最优路径应该是从(0, n-1)移动到(n-2, n-1),并且不能越过主对角线。因此,最优解中第二个小朋友一定不会碰到主对角线。
需要特别处理如何从(n-2, n-1)出发,并且确保最终能精确到达(0, n-1)。每次规划路径时,我们需要确保每个小朋友的路径不会重叠,并且他们的水果收集路径最大化。 - 边界条件处理
对于第二个小朋友,最关键的是每次的 j 必须满足j >= n - 1 - i,确保路径不会越过对角线。
通过递归和记忆化搜索的方式,计算每个小朋友的最大水果收集数量。 - 动态规划实现
通过递归和记忆化搜索,我们可以解决这个问题。下面是实现代码:
class Solution {
public:int maxCollectedFruits(vector<vector<int>>& fruits) {int n = fruits.size(), res = 0;vector<vector<int>> memo(n, vector<int>(n, -1)); // 记忆化数组// 记忆化搜索函数function<int(int, int)> dfs = [&](int r, int c) -> int {if (r == 0) return fruits[r][c];if (memo[r][c] != -1) return memo[r][c]; // 如果已计算,直接返回for (int i = -1; i <= 1; i++) {int y = c + i;if (y >= n || y < n - 1 - (r - 1)) continue; // 确保列范围合法memo[r][c] = max(memo[r][c], dfs(r - 1, y) + fruits[r][c]);}return memo[r][c];};// 计算第一个小朋友的收集水果for (int i = 0; i < n; i++) {res += fruits[i][i];}res += dfs(n - 2, n - 1); // 从下往上走,第二个小朋友的收集路径// 将下三角形的数据填充到上三角for (int i = 0; i < n; i++) {for (int j = i; j < n; j++) {fruits[i][j] = fruits[j][i];}}// 重置memo数组并计算第三个小朋友的收集路径std::fill_n(memo.begin(), n, std::vector<int>(n, -1));res += dfs(n - 2, n - 1);return res;}
};
- 思路总结
记忆化搜索:通过递归的方式计算每个小朋友的最大水果收集数量,并利用记忆化缓存避免重复计算。
路径规划:根据每个小朋友的移动规则,避免路径重叠,并确保每个小朋友能够最大化收集水果。
矩阵转置:对于第二个小朋友和第三个小朋友,可以通过对矩阵进行转置操作,简化计算。
相关文章:

最多可收集的水果数目
三个小朋友收集水果问题:最大水果收集路径 问题描述 有一个游戏,游戏由 n x n 个房间网格状排布组成。给定一个大小为 n x n 的二维整数数组 fruits,其中 fruits[i][j] 表示房间 (i, j) 中的水果数目。 游戏开始时,三个小朋友分…...

戴尔 AI Factory 上的 Agentic RAG 搭载 NVIDIA 和 Elasticsearch 向量数据库
作者:来自 Elastic Hemant Malik, Dell Team 我们很高兴与戴尔合作撰写白皮书《戴尔 AI Factory with NVIDIA 上的 Agentic RAG》。白皮书是一份供开发人员参考的设计文档,概述了实施 Agentic 检索增强生成 (retrieval augmented generation - RAG) 应用…...

HarmonyOS4+NEXT星河版入门与项目实战(16)------ 状态管理 @State(页面数据刷新与渲染)
文章目录 1、@State装饰器2、视图渲染演示1、无嵌套的对象属性值变化时可以触发页面渲染2、嵌套对象的嵌套属性值变化时不能够触发页面刷新渲染3、数组中对象的属性值变化时不能触发页面刷新渲染3、总结1、@State装饰器 2、视图渲染演示 常规的 string、number 这里就不演示了…...

Origin教程003:数据导入(2)-从文件导入和导入矩阵数据
文章目录 3.3 从文件导入3.3.1 导入txt文件3.3.2 导入excel文件3.3.3 合并工作表3.4 导入矩阵数据3.3 从文件导入 所需数据 https://download.csdn.net/download/WwLK123/900267473.3.1 导入txt文件 选择【数据->从文件导入->导入向导】: 选择文件之后,点击完成即可…...

设计自己的网络通信协议
文章目录 一、为什么需要设计网络通信协议1. **标准化通信规则**2. **确保数据传输的可靠性**3. **支持网络的多样性和可扩展性**4. **分层设计,简化复杂性**5. **实现设备的互操作性**6. **支持多任务和多应用并发**7. **提供安全性**8. **支持不同的通信模式**总结…...

深入理解 Seata:分布式事务的最佳解决方案
随着微服务架构的广泛应用,分布式事务管理成为系统设计中一项重要且极具挑战的任务。在微服务架构下,服务之间通过网络调用,单个业务操作往往需要多个服务的协作来完成,这样分布式事务的问题就不可避免。Seata 是目前较为流行的一…...

JDK下载
jdk-8u421-windows-x64.exe : 阿里云盘 jdk-7u80-windows-x64.exe :阿里云盘...

如何使用 Python 开发一个简单的文本数据转换为 Excel 工具
目录 一、准备工作 二、理解文本数据格式 三、开发文本数据转换为Excel工具 读取CSV文件 将DataFrame写入Excel文件 处理其他格式的文本数据 读取纯文本文件: 读取TSV文件: 四、完整代码与工具封装 五、使用工具 六、总结 在数据分析和处理的日常工作中,我们经常…...

React(六)——Redux
文章目录 项目地址基本理解一、配置Redux store二、创建slice配置到store里并使用三、给Slice配置reducers,用来修改初始值 项目地址 教程作者:教程地址: 代码仓库地址: 所用到的框架和插件: dbt airflow基本理解 s…...

java抽奖系统(二)
3. 新建项目 3.1 选择相应的框架 pom文件配置如下: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:s…...

STM32F10x 定时器
使用定时器实现:B5 E5的开关 添加相关的.h路径文件 添加相关的.c配置文件 led.h文件 用于声明LED函数 #ifndef __LED_H //没有定义__LED_H #define __LED_H //就定义__LED_H #define LED1_ON GPIO_ResetBits(GPIOB,GPIO_Pin_5) #defi…...

从0开始学PHP面向对象内容之常用设计模式(适配器,桥接,装饰器)
二,结构型设计模式 上两期咱们讲了创建型设计模式,都有 单例模式,工厂模式,抽象工厂模式,建造者模式,原型模式五个设计模式。 这期咱们讲结构型设计模式 1、适配器模式(Adapter) …...

玩转数字与运算:用C语言实现24点游戏的扑克牌魅力
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

前端入门之VUE--基础与核心
前言 VUE是前端用的最多的框架;这篇文章是本人大一上学习前端的笔记;欢迎点赞 收藏 关注,本人将会持续更新。 Vue学习笔记 用于构建用户界面的渐进式框架 构建用户界面:基于数据动态渲染页面渐进式:循序渐近的学…...

logback 初探学习
logback 三大模块 记录器(Logger)、追加器(Appender)和布局(Layout) 配置文件外层最基本的标签如图示 xml中定义的就是这个三个东西下面进入学习 包引入参考springboot 官方文档 Logging :: Spring Boo…...

在Elasticsearch中,是怎么根据一个词找到对应的倒排索引的?
大家好,我是锋哥。今天分享关于【在Elasticsearch中,是怎么根据一个词找到对应的倒排索引的?】面试题。希望对大家有帮助; 在Elasticsearch中,是怎么根据一个词找到对应的倒排索引的? 在 Elasticsearch 中…...
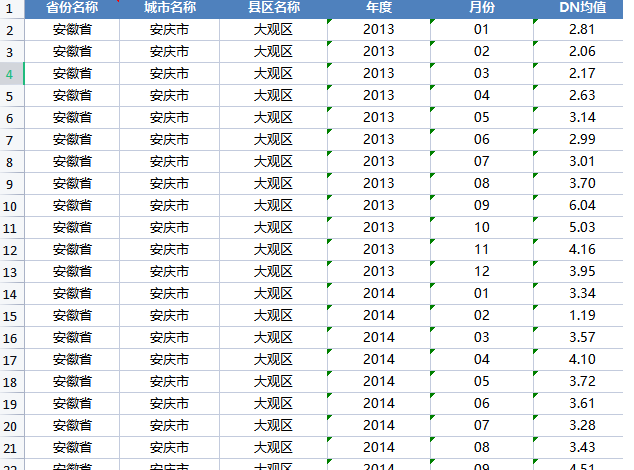
1992-2021年 各省市县经过矫正的夜间灯光数据(GNLD、VIIRS)区域汇总:省份、城市、区县面板数据
1992-2021年 各省市县经过矫正的夜间灯光数据(GNLD、VIIRS)区域汇总:省份、城市、区县面板数据 .r.rar https://download.csdn.net/download/2401_84585615/90001905 从1992年至2021年,中国各省份、城市及区县的夜间灯光数据经过…...

linux实战-黑链——玄机靶场
黑链的特征: 隐藏链接:黑链通常隐藏在网站页面中,使用CSS、JavaScript或其他手段使其对普通用户不可见,但仍然能被搜索引擎爬虫检测到。恶意内容:这些链接指向的内容可能包含恶意软件、钓鱼页面或其他不良内容&#x…...

鸿蒙NEXT开发案例:字数统计
【引言】 本文将通过一个具体的案例——“字数统计”组件,来探讨如何在鸿蒙NEXT框架下实现这一功能。此组件不仅能够统计用户输入文本中的汉字、中文标点、数字、以及英文字符的数量,还具有良好的用户界面设计,使用户能够直观地了解输入文本…...

uniapp vue2项目迁移vue3项目
uniapp vue2项目迁移vue3项目,必须适配的部分 一、main.js 创建应用实例 // 之前 - Vue 2 import Vue from vue import App from ./App Vue.config.productionTip false // vue3 不再需要 App.mpType app // vue3 不再需要 const app new Vue({ ...App }) …...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
