回溯法经典难题解析
本文将通过几个经典的回溯问题,展示回溯算法的应用及其在解决问题时的核心思想和技巧。这些问题包括全排列、全排列II、N皇后以及数独问题,本文将分别介绍每个问题的思路与实现。
46. 全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
思路:
对于给定的数组,我们通过回溯法逐一选择数组中的元素,并将其加入当前的排列中。
需要一个 visited 数组来记录每个元素是否已经被使用过,避免重复排列。
每当排列的长度等于原数组长度时,表示当前排列已完成,加入结果集。
核心技巧:
在递归过程中使用 visited 数组来确保每个元素只被使用一次。
递归的终止条件是当当前排列的长度等于数组长度时,说明已经形成一个完整的排列。
class Solution {
public:vector<vector<int>> res;vector<int> path;unordered_set<int> node;void backfind(vector<int>& nums){if(path.size()==nums.size()){res.push_back(path);return;}for(int i=0; i<nums.size(); i++){if(node.find(nums[i])!=node.end()){continue;}node.insert(nums[i]);path.push_back(nums[i]);backfind(nums);node.erase(nums[i]);path.pop_back();}}vector<vector<int>> permute(vector<int>& nums) {backfind(nums);return res;}
};
47. 全排列 II
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],[1,2,1],[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
思路:先对数组进行排序,使得相同的元素相邻。使用 visited 数组来标记每个元素是否已经被访问过,同时利用排序后的数组来跳过已经处理过的重复元素。在每次递归时,检查当前元素与前一个元素是否相同,如果相同且前一个元素未被访问,则跳过当前元素。
核心技巧:排序保证了相同元素相邻,从而避免了重复排列。通过回溯的剪枝技巧,避免在同一层的递归中重复访问相同的元素。
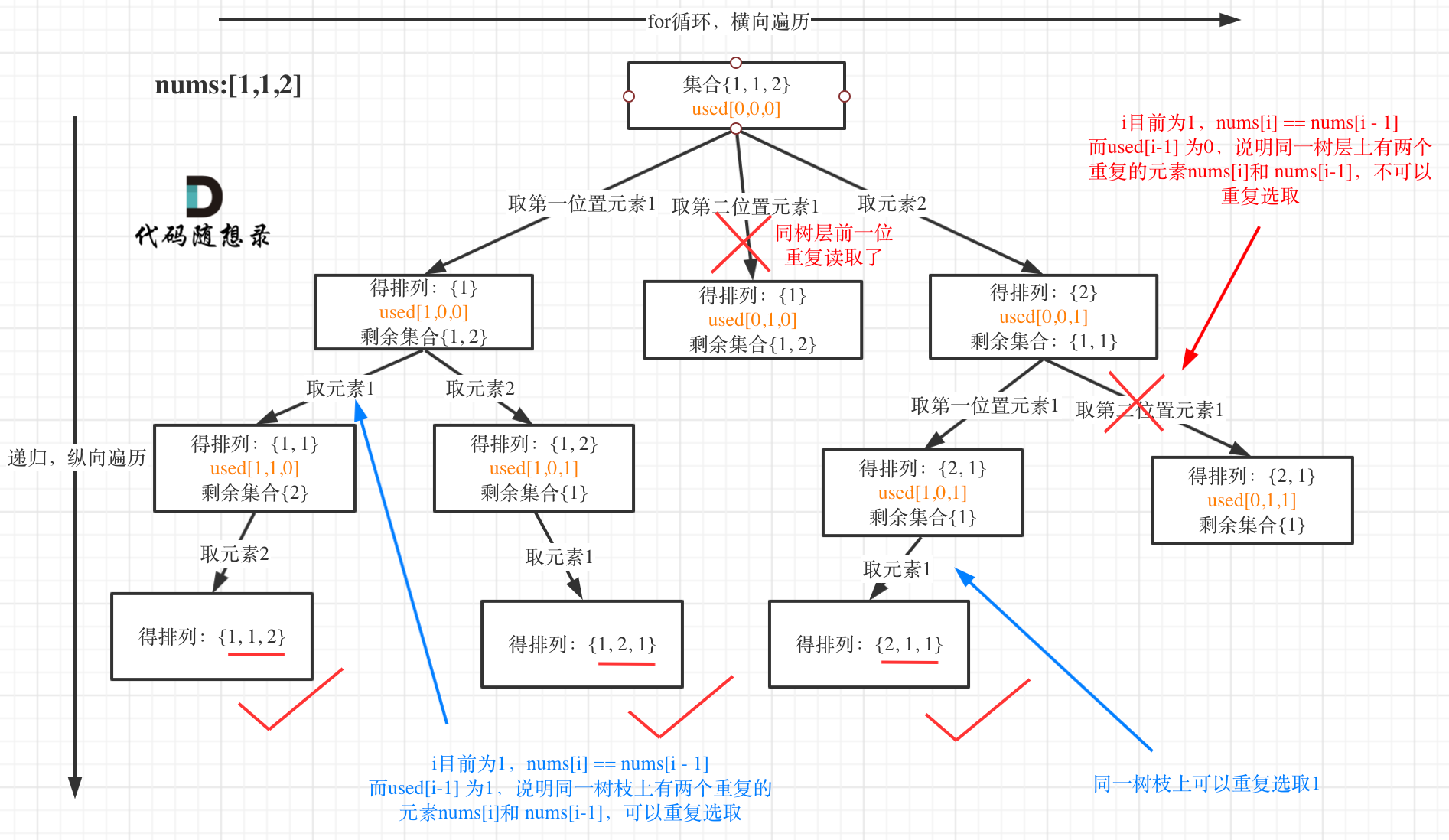
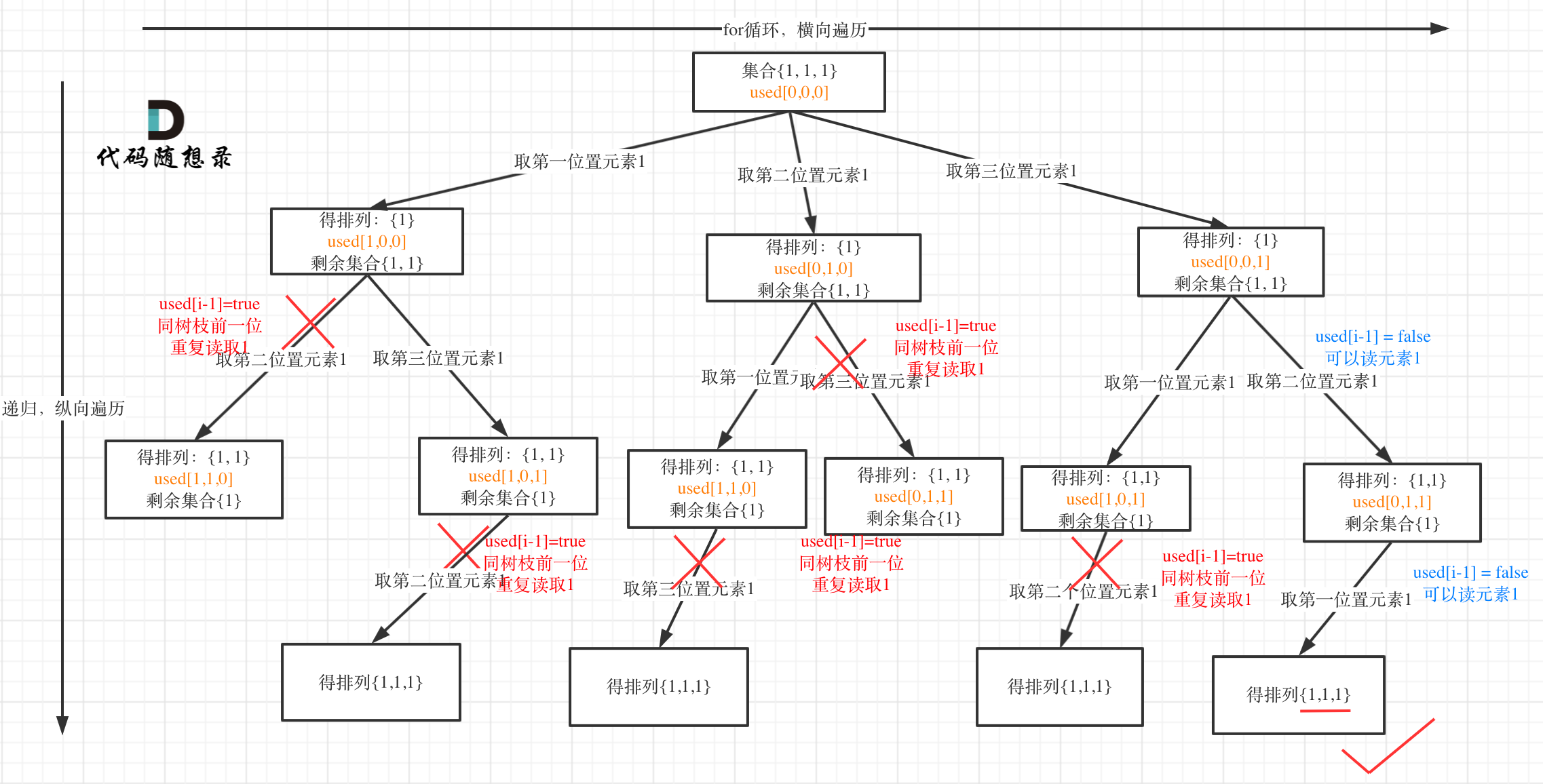
class Solution {
public:vector<vector<int>> res;vector<int> path;void backfind(vector<int>& nums, vector<bool>& visited){if(path.size()==nums.size()){res.push_back(path);return; }for(int i=0; i<nums.size(); i++){if(i>0&&nums[i]==nums[i-1]&&visited[i-1]==false){continue;}//同层树重复的跳过,同层的上一个visited是没访问过的(回溯)//visited[i-1]==true也是可以滴if(visited[i]){continue;}visited[i]=true;path.push_back(nums[i]);backfind(nums,visited);visited[i]=false;path.pop_back();}}vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(), nums.end());vector<bool> visited(nums.size(), false);backfind(nums,visited);return res;}
};
51. N 皇后
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
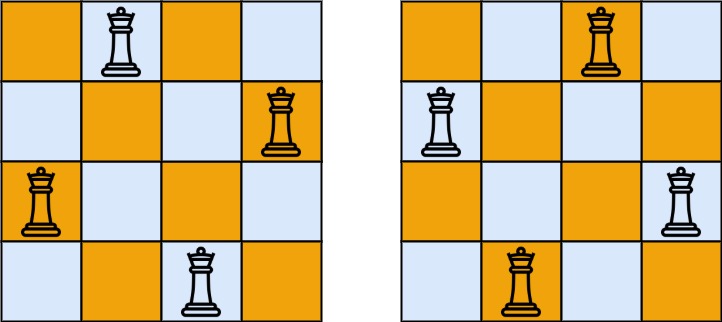
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
思路:使用回溯法逐行放置皇后,每放置一个皇后就递归处理下一行。
在每次尝试放置皇后时,检查该位置是否会与已放置的皇后发生冲突,即检查同列、左斜线和右斜线是否已有皇后。
核心技巧:使用三种标记(列标记、左斜线标记、右斜线标记)来有效判断是否可以放置皇后。
通过递归实现行的逐步尝试,并在放置皇后后继续处理下一行。
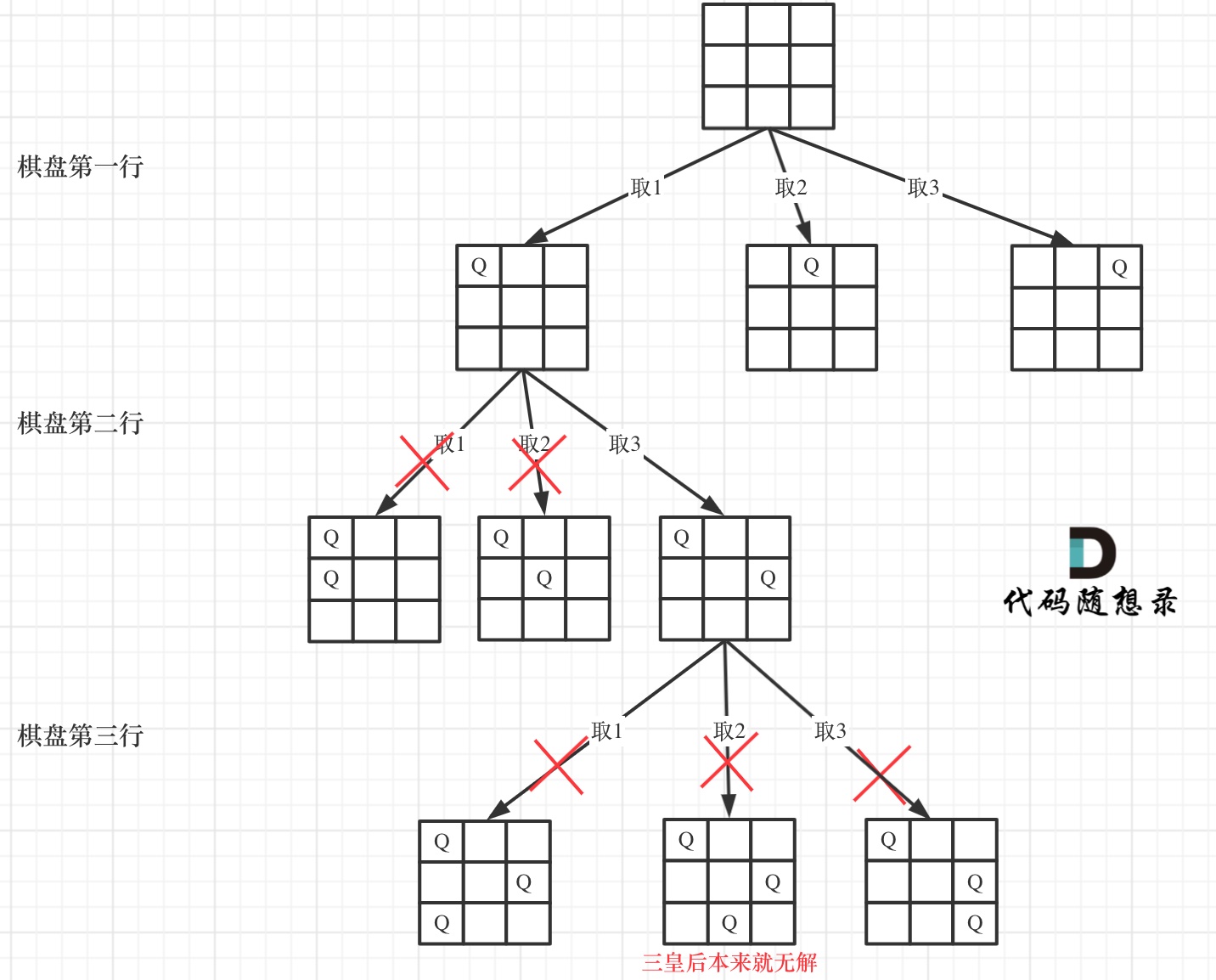
class Solution {
public:vector<vector<string>> res;void find(int n, int row, vector<string>& rowChess){if(row==n){res.push_back(rowChess);return;}for(int col=0; col<n; col++){if(isQ(rowChess,row,col,n)){rowChess[row][col]='Q';find(n, row+1, rowChess);rowChess[row][col]='.';}}}bool isQ(vector<string>& rowChess, int row, int col, int n){//先遍历列for(int i=0; i<row; i++){if(rowChess[i][col]=='Q'){return false;}}//再检查45°线for(int i=row-1, j=col-1; i>=0&&j>=0; i--,j--){if(rowChess[i][j]=='Q'){return false;}}//再检查135°线for(int i=row-1, j=col+1; i>=0&&j<n; i--,j++){if(rowChess[i][j]=='Q'){return false;}}return true;}vector<vector<string>> solveNQueens(int n) {vector<string> rowChess(n, string(n,'.'));find(n, 0, rowChess);return res;}
};
37. 解数独
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。
思路:使用回溯法逐步填充数独中的空格。每次选择一个空格,尝试填入数字 1-9,并检查填入的数字是否合法。如果合法,递归处理下一个空格;如果不合法,回溯并尝试其他数字。
核心技巧:使用一个 isOK 函数来检查当前填入的数字是否符合数独的规则。
回溯的终止条件是所有空格都被填充且合法时,返回解。
class Solution {
public:bool backsolve(vector<vector<char>>& board){for(int i=0; i<board.size(); i++){for(int j=0; j<board[0].size(); j++){if(board[i][j]=='.'){for(char c='1'; c<='9'; c++){if(isOK(board,i,j,c)){board[i][j]=c;if(backsolve(board)) return true;board[i][j]='.';}}return false;}}}return true;}bool isOK(vector<vector<char>>& board, int row, int col, char val){//行里面寻找有没有重复的for(int i=0; i<9; i++){if(board[i][col]==val){return false;}}//列里面寻找有没有重复的for(int j=0; j<9; j++){if(board[row][j]==val){return false;}}int startrow=(row/3)*3;int startcol=(col/3)*3;for(int i=startrow; i<startrow+3; i++){for(int j=startcol; j<startcol+3; j++){if(board[i][j]==val){return false;}}}return true;}void solveSudoku(vector<vector<char>>& board) {backsolve(board);}
};
相关文章:

回溯法经典难题解析
本文将通过几个经典的回溯问题,展示回溯算法的应用及其在解决问题时的核心思想和技巧。这些问题包括全排列、全排列II、N皇后以及数独问题,本文将分别介绍每个问题的思路与实现。 46. 全排列 给定一个不含重复数字的数组 nums ,返回其 所有…...

LLM的原理理解6-10:6、前馈步骤7、使用向量运算进行前馈网络的推理8、注意力层和前馈层有不同的功能9、语言模型的训练方式10、GPT-3的惊人性能
目录 LLM的原理理解6-10: 6、前馈步骤 7、使用向量运算进行前馈网络的推理 8、注意力层和前馈层有不同的功能 注意力:特征提取 前馈层:数据库 9、语言模型的训练方式 10、GPT-3的惊人性能 一个原因是规模 大模型GPT-1。它使用了768维的词向量,共有12层,总共有1.…...

Electron开发构建工具electron-vite(alex8088)添加VueDevTools(VitePlugin)
零、介绍 本文章的electron-vite指的是这个项目👉electron-vite仓库,electron-vite网站 本文章的VueDevTools指的是VueDevTools的Vite插件版👉https://devtools.vuejs.org/guide/vite-plugin 一、有一个用electron-vite创建的项目 略 二、…...

【C++】static修饰的“静态成员函数“--静态成员在哪定义?静态成员函数的作用?
声明为static的类成员称为类的静态成员,用static修饰的成员变量,称之为静态成员变量;用 static修饰的成员函数,称之为静态成员函数。静态成员变量一定要在类外进行初始化 一、静态成员变量 1)特性 所有静态成员为所有类对象所共…...
 =ref())
=computed() =ref()
computed() ref() 在 Vue 中,computed() 和 ref() 是 Vue 3 组合式 API 的核心工具,它们分别用于 计算属性 和 响应式数据。以下是它们的区别和用法: 1. ref() 作用 用于创建响应式的单一数据。可以是基本类型(如字符串、数字、…...

webgl threejs 云渲染(服务器渲染、后端渲染)解决方案
云渲染和流式传输共享三维模型场景 1、本地无需高端GPU设备即可提供三维项目渲染 云渲染和云流化媒体都可以让3D模型共享变得简单便捷。配备强大GPU的远程服务器早就可以处理密集的处理工作,而专有应用程序,用户也可以从任何个人设备查看全保真模型并与…...

【shell编程】函数、正则表达式、文本处理工具
函数 系统函数 常见内置命令 echo打印输出 #!/bin/bash # 输出普通文本 echo "Hello, World!"# 输出变量值 name"Alice" echo "Hello, $name"# 输出带有换行符的文本 echo -n "Hello, " # -n 选项不输出换行 echo "World!&quo…...
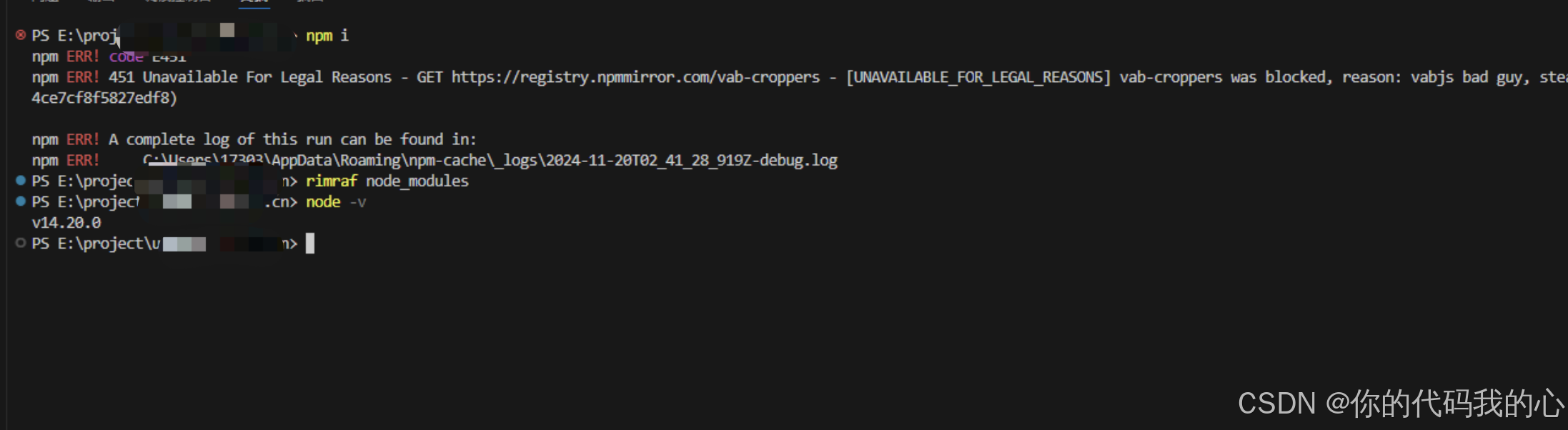
解决 npm xxx was blocked, reason: xx bad guy, steal env and delete files
问题复现 今天一位朋友说,vue2的老项目安装不老依赖,报错内容如下: npm install 451 Unavailable For Legal Reasons - GET https://registry.npmmirror.com/vab-count - [UNAVAILABLE_FOR_LEGAL_REASONS] vab-count was blocked, reas…...

如何进行高级红队测试:OpenAI的实践与方法
随着人工智能(AI)技术的迅猛发展,AI模型的安全性和可靠性已经成为业界关注的核心问题之一。为了确保AI系统在实际应用中的安全性,红队测试作为一种有效的安全评估方法,得到了广泛应用。近日,OpenAI发布了两…...

Java:二维数组
目录 1. 二维数组的基础格式 1.1 二维数组变量的创建 —— 3种形式 1.2 二维数组的初始化 \1 动态初始化 \2 静态初始化 2. 二维数组的大小 和 内存分配 3. 二维数组的不规则初始化 4. 遍历二维数组 4.1 for循环 编辑 4.2 for-each循环 5. 二维数组 与 方法 5.1…...
Android 天气APP(三十七)新版AS编译、更新镜像源、仓库源、修复部分BUG
上一篇:Android 天气APP(三十六)运行到本地AS、更新项目版本依赖、去掉ButterKnife 新版AS编译、更新镜像源、仓库源、修复部分BUG 前言正文一、更新镜像源① 腾讯源③ 阿里源 二、更新仓库源三、修复城市重名BUG四、地图加载问题五、源码 前…...
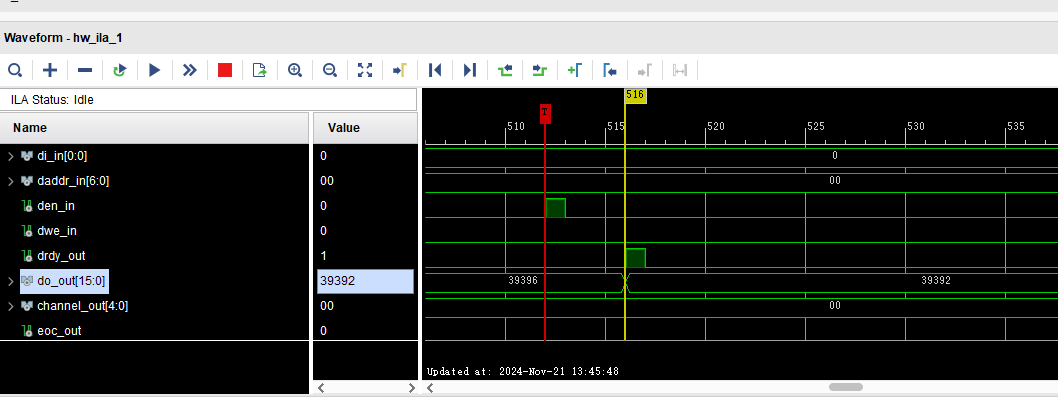
Xilinx IP核(3)XADC IP核
文章目录 1. XADC介绍2.输入要求3.输出4.XADC IP核使用5.传送门 1. XADC介绍 xadc在 所有的7系列器件上都有支持,通过将高质量模拟模块与可编程逻辑的灵活性相结合,可以为各种应用打造定制的模拟接口,XADC 包括双 12 位、每秒 1 兆样本 (MSP…...
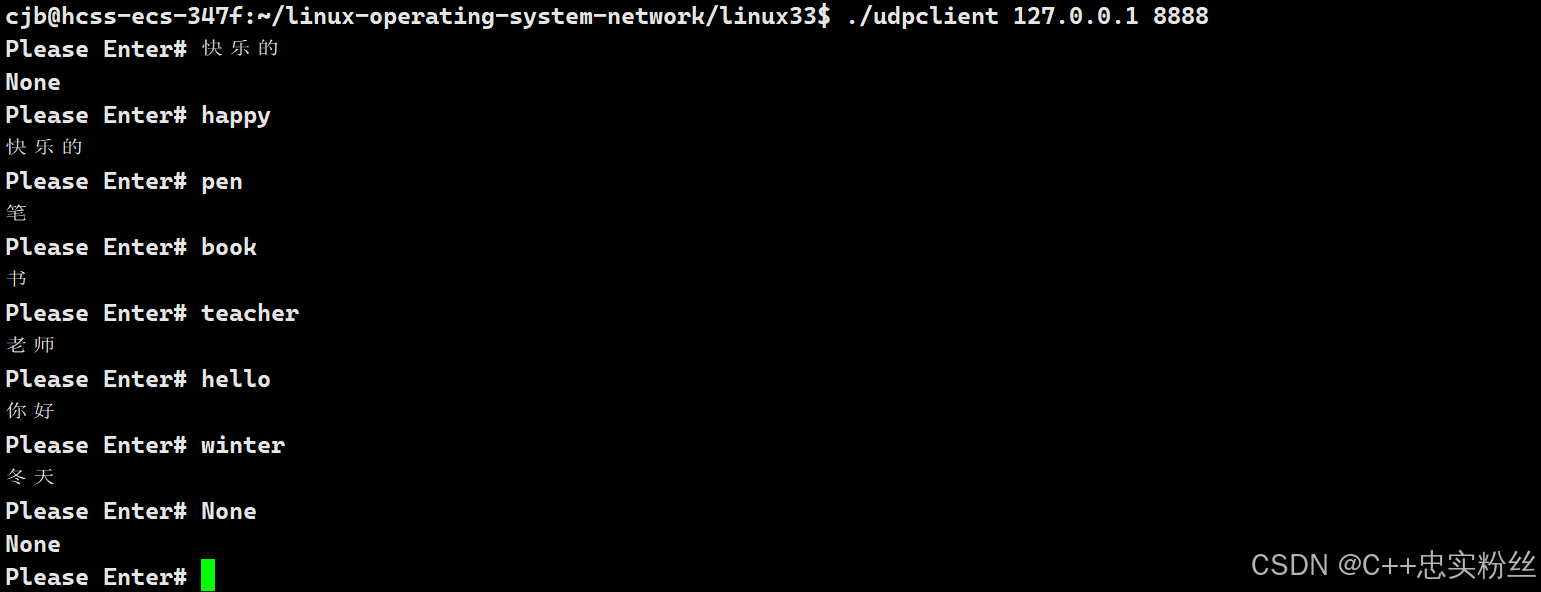
计算机网络socket编程(2)_UDP网络编程实现网络字典
个人主页:C忠实粉丝 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 C忠实粉丝 原创 计算机网络socket编程(2)_UDP网络编程实现网络字典 收录于专栏【计算机网络】 本专栏旨在分享学习计算机网络的一点学习笔记,欢迎大家在评论区交流讨…...
c#窗体列表框(combobox)应用——省市区列表选择实例
效果如下: designer.cs代码如下: using System.Collections.Generic;namespace 删除 {public partial class 省市区选择{private Dictionary<string, List<string>> provinceCityDictionary;private Dictionary<string,List<string&…...

Nginx 架构与设计
Nginx 是一个高性能的 HTTP 和反向代理服务器,同时也可以用作邮件代理和通用的 TCP/UDP 负载均衡器。它的架构设计以高并发、高可扩展性和高性能为目标,充分利用操作系统提供的多路复用机制和事件驱动模型。以下是 Nginx 的架构和设计特点: 1…...
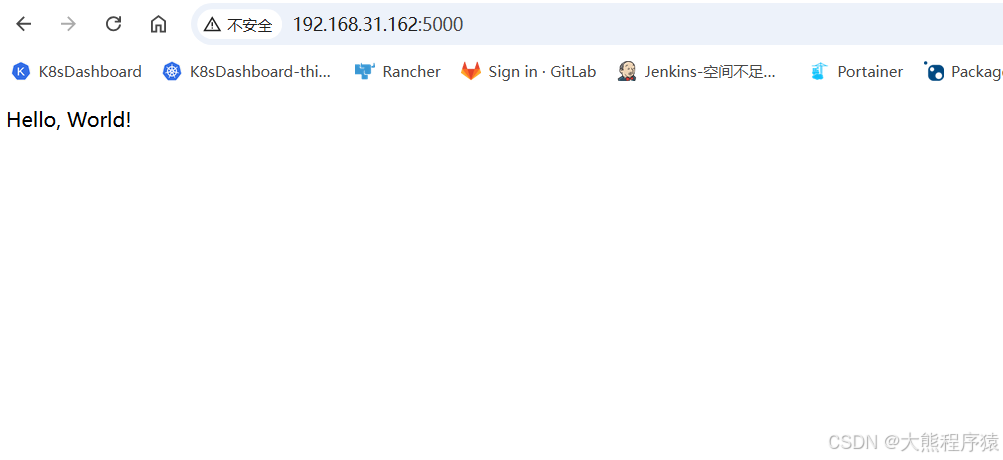
python Flask指定IP和端口
from flask import Flask, request import uuidimport json import osapp Flask(__name__)app.route(/) def hello_world():return Hello, World!if __name__ __main__:app.run(host0.0.0.0, port5000)...

多线程 相关面试集锦
什么是线程? 1、线程是操作系统能够进⾏运算调度的最⼩单位,它被包含在进程之中,是进程中的实际运作单位,可以使⽤多线程对 进⾏运算提速。 ⽐如,如果⼀个线程完成⼀个任务要100毫秒,那么⽤⼗个线程完成改…...
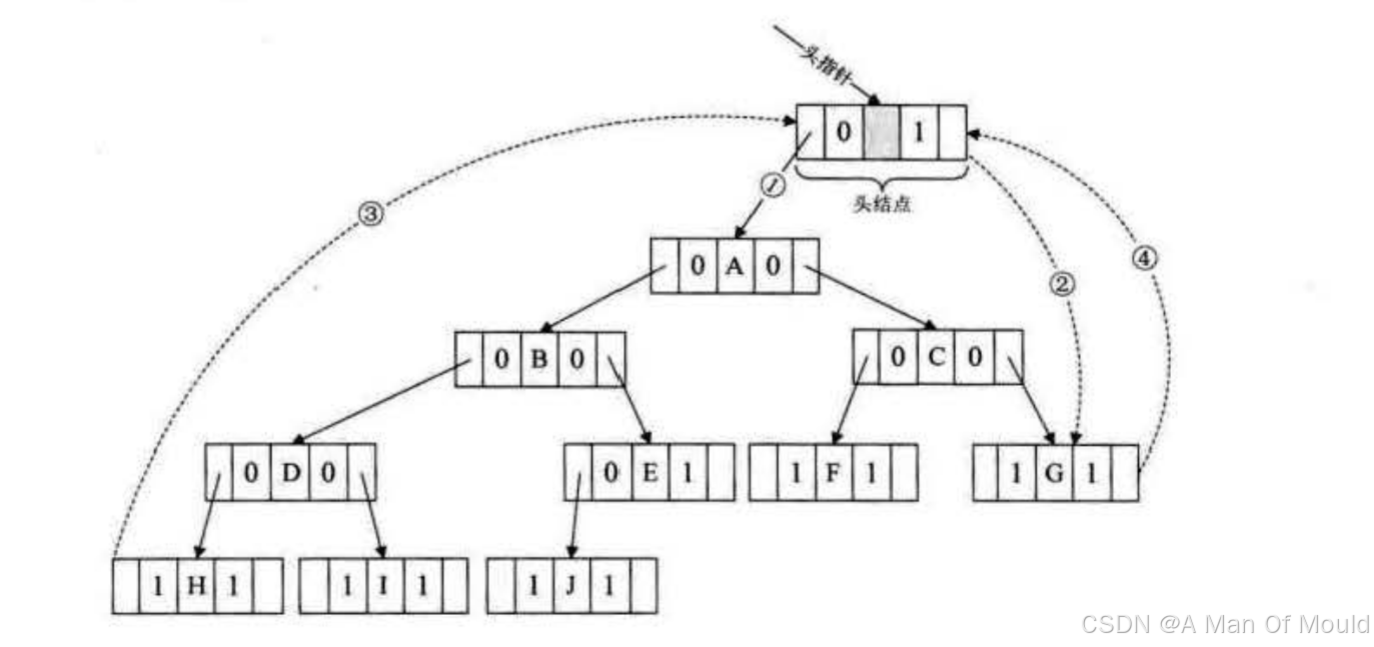
【数据结构】—— 线索二叉树
引入 我们现在提倡节约型杜会, 一切都应该节约为本。对待我们的程序当然也不例外,能不浪费的时间或空间,都应该考虑节省。我们再观察团下图的二叉树(链式存储结构),会发现指针域并不是都充分的利用了,有许…...
uni-app 发布媒介功能(自由选择媒介类型的内容) 设计
1.首先明确需求 我想做一个可以选择媒介的内容,来进行发布媒介的功能 (媒介包含:图片、文本、视频) 2.原型设计 发布-编辑界面 通过点击下方的加号,可以自由选择添加的媒介类型 但是因为预览中无法看到视频的效果&…...
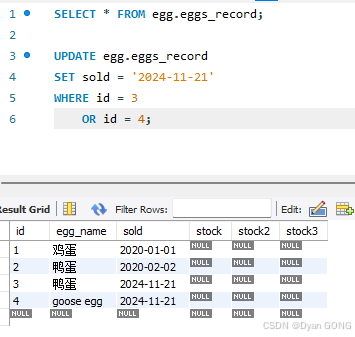
How to update the content of one column in Mysql
How to update the content of one column in Mysql by another column name? UPDATE egg.eggs_record SET sold 2024-11-21 WHERE id 3 OR id 4;UPDATE egg.eggs_record SET egg_name duck egg WHERE id 2;...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...
