如何在 .gitignore 中仅保留特定文件:以忽略文件夹中的所有文件为例
在日常的开发工作中,使用 Git 来管理项目是不可或缺的一部分。项目中的某些文件夹可能包含大量的临时文件、生成文件或不需要版本控制的文件。在这种情况下,我们通常会使用 .gitignore 文件来忽略这些文件夹。然而,有时我们可能希望在忽略整个文件夹的同时,保留其中的某些特定文件。
本文将介绍如何在 .gitignore 中配置规则,以仅保留某个文件夹中的特定文件。
基本概念
.gitignore 文件用于告诉 Git 哪些文件或文件夹应该被忽略,哪些应该被跟踪。当我们想要忽略一个文件夹中的所有内容时,可以使用通配符 * 来非常方便地实现。但是,如果我们需要保留该文件夹中的某些特定文件,就需要引入否定模式。
示例场景
假设我们有一个文件夹 example_folder,该文件夹中有多个文件和子文件夹。我们希望忽略该文件夹中的所有内容,但保留一个名为 keep.txt 的文件。
.gitignore 配置
以下是实现这一需求的 .gitignore 文件配置:
plaintext
忽略 example_folder 下的所有文件
example_folder/*
但保留 keep.txt
!example_folder/keep.txt
配置解释
example_folder/*:
这一行表示忽略 example_folder 文件夹下的所有文件和子文件夹。* 是一个通配符,匹配文件夹中的所有内容。
!example_folder/keep.txt:
这是一个否定模式,表示不忽略 keep.txt 文件。叹号 ! 用于排除某些文件或文件夹,使其不被忽略。
注意事项
规则顺序: .gitignore 中的规则是按顺序应用的。因此,否定规则(即以 ! 开头的规则)必须放在相应的忽略规则之后,才能生效。
子文件夹中的文件: 如果你需要在子文件夹中保留特定文件,确保父文件夹没有被忽略。例如,如果你想保留 example_folder/sub_folder/special.txt,你需要在 .gitignore 中明确指定。
扩展应用
如果你有多个文件需要保留,只需为每个文件添加对应的否定规则。例如:
plaintext
忽略 example_folder 下的所有文件
example_folder/*
但保留 keep.txt 和 another_file.txt
!example_folder/keep.txt
!example_folder/another_file.txt
这样配置后,Git 只会跟踪 keep.txt 和 another_file.txt,而忽略其他内容。
总结
通过正确配置 .gitignore 文件,我们可以灵活地管理哪些文件需要版本控制,哪些不需要。这不仅简化了代码管理,还能提高项目的运行效率。希望本文能帮助你更好地使用 .gitignore,实现更精细的文件管理。
对于更多关于 Git 和版本控制的文章,请关注我的 CSDN 博客。欢迎留言和交流!
相关文章:

如何在 .gitignore 中仅保留特定文件:以忽略文件夹中的所有文件为例
在日常的开发工作中,使用 Git 来管理项目是不可或缺的一部分。项目中的某些文件夹可能包含大量的临时文件、生成文件或不需要版本控制的文件。在这种情况下,我们通常会使用 .gitignore 文件来忽略这些文件夹。然而,有时我们可能希望在忽略整个…...

详解八大排序(一)------(插入排序,选择排序,冒泡排序,希尔排序)
文章目录 前言1.插入排序(InsertSort)1.1 核心思路1.2 实现代码 2.选择排序(SelectSort)2.1 核心思路2.2 实现代码 3.冒泡排序(BubbleSort)3.1 核心思路3.2 实现代码 4.希尔排序(ShellSort&…...

Linux虚拟机空间扩容(新增磁盘并分区挂载)
1、命令shutdown -h now关闭虚拟机(要关机后再进行新增磁盘操作) 云平台进入虚拟机管理,新增磁盘 成功添加一块100G的磁盘 3、在Linux终端下执行该命令:lsblk 发现有新添加的磁盘。 也新增了/dev/vdb 3、分区 输入命令࿱…...

数据结构 ——— 直接选择排序算法的实现
目录 直接选择排序算法的思想 优化直接选择排序算法的思想 代码实现(默认升序) 直接选择排序算法的思想 直接选择排序算法的思想类似与直接插入排序 区别在于从大到小选择最小的元素或者最大的元素直接放在元素应该停留的位置每次从待排序的元素中选…...

MySQL中的ROW_NUMBER窗口函数简单了解下
ROW_NUMBER() 是 MySQL8引入的窗口函数之一,它为查询结果集中的每一行分配一个唯一的顺序号(行号)。这个顺序号是基于窗口函数的 ORDER BY 子句进行排序的,可以根据指定的排序顺序生成连续的整数值。 ROW_NUMBER() 在分页、去重、…...

day24|leetCode 93.复原IP地址 , 78.子集 , 90.子集II
8.复原ip地址 有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 . 分隔。 例如:"0.1.2.201" 和"192.168.1.1" 是 有效 IP 地址,但是 "…...

RocketMQ: Broker 使用指南
Broker 配置参数 获取 Broker 的默认配置 $ sh mqbroker -m Broker 启劢时,如何加载配置 ### 第一步生成 Broker 默认配置模版 sh mqbroker -m > broker.p ### 第二步修改配置文件, broker.p ### 第三步加载修改过的配置文件 nohup sh mqbroker -c broker.pBrok…...

【Linux 篇】Docker 的容器之海与镜像之岛:于 Linux 系统内探索容器化的奇妙航行
文章目录: 【Linux 篇】Docker 的容器之海与镜像之岛:于 Linux 系统内探索容器化的奇妙航行前言安装docker-centos7 【Linux 篇】Docker 的容器之海与镜像之岛:于 Linux 系统内探索容器化的奇妙航行 💬欢迎交流:在学习…...

5、AI测试辅助-生成测试用例思维导图
AI测试辅助-生成测试用例思维导图 创建测试用例两种方式1、Plantuml思维导图版本 (不推荐)2、Markdown思维导图版本(推荐) 创建测试用例两种方式 完整的测试用例通常需要包含以下的元素: 1、测试模块 2、测试标题 3、前置条件 4、…...

nature communications论文 解读
题目《Transfer learning with graph neural networks for improved molecular property prediction in the multi-fidelity setting》 这篇文章主要讨论了如何在多保真数据环境(multi-fidelity setting)下,利用图神经网络(GNNs&…...

基于Java Springboot公园管理系统
一、作品包含 源码数据库设计文档万字PPT全套环境和工具资源部署教程 二、项目技术 前端技术:Html、Css、Js、Vue、Element-ui 数据库:MySQL 后端技术:Java、Spring Boot、MyBatis 三、运行环境 开发工具:IDEA/eclipse 数据…...

神经网络(系统性学习三):多层感知机(MLP)
相关文章: 神经网络中常用的激活函数 神经网络(系统性学习一):入门篇 神经网络(系统性学习二):单层神经网络(感知机) 多层感知机(MLP) 多层感…...

07-SpringCloud-Gateway新一代网关
一、概述 1、Gateway介绍 官网:https://spring.io/projects/spring-cloud-gateway Spring Cloud Gateway组件的核心是一系列的过滤器,通过这些过滤器可以将客户端发送的请求转发(路由)到对应的微服务。 Spring Cloud Gateway是加在整个微服务最前沿的防…...

HTML 表单实战:从创建到验证
HTML表单是用于收集用户输入数据的一种方式,可以用于创建各种类型的表单,例如登录表单、注册表单、调查问卷表单等。本文将详细介绍表单元素的使用,并利用JavaScript实现对表单数据的验证。 HTML表单元素的使用 输入框<input> <i…...

【redis 】string类型详解
string类型详解 一、string类型的概念二、string类型的常用指令2.1 SET2.2 GET2.3 MSET2.4 MGET2.5 SETNX2.6 INCR2.7 INCRBY2.8 DECR2.9 DECRBY2.10 INCRBYFLOAT2.11 APPEND2.12 GETRANGE2.13 SETRANGE2.14 STRLEN 三、string类型的命令小结四、string类型的内部编码五、strin…...
Vue.js 学习总结(13)—— Vue3 version 计数介绍
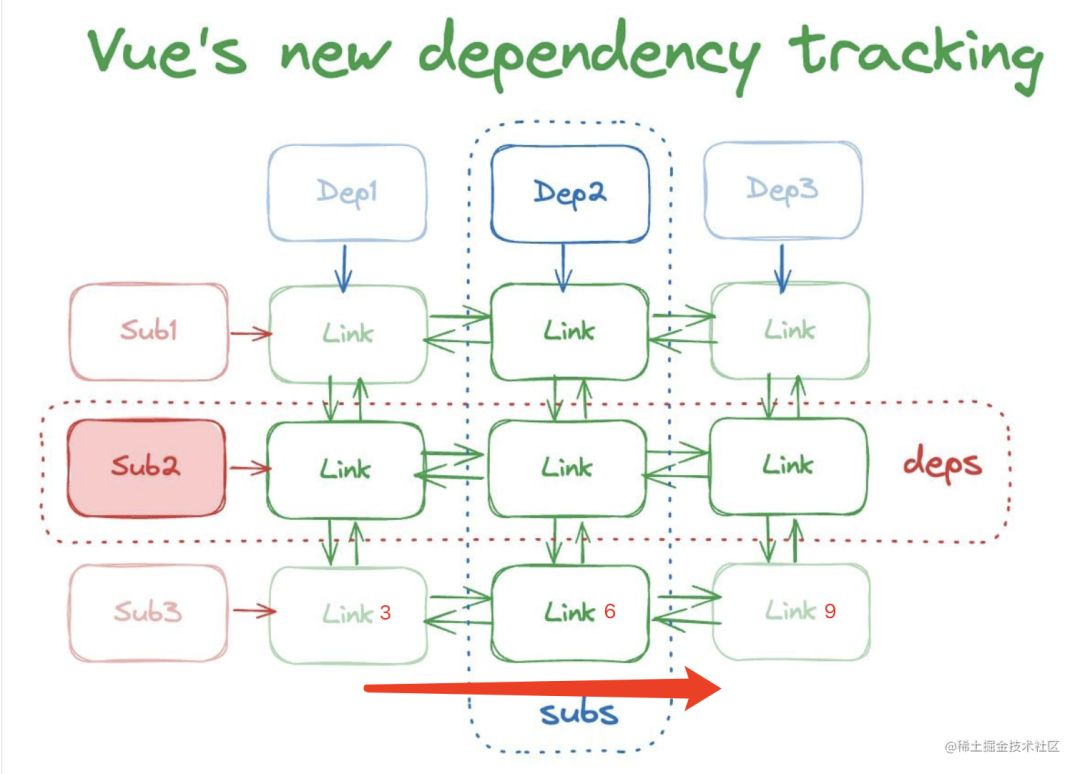
前言 Vue3.5 提出了两个重要概念:version计数和双向链表,作为在内存和计算方面性能提升的最大功臣。既然都重要,那就单挑 version 计数来介绍,它在依赖追踪过程中,起到快速判断依赖项有没有更新的作用,所以…...

【数据结构】【线性表】一文讲完队列(附C语言源码)
队列 队列的基本概念基本术语基本操作 队列的顺序实现顺序队列结构体的创建顺序队列的初始化顺序队列入队顺序队列出队顺序队列存在的问题分析循环队列代码汇总 队列的链式实现链式队列的创建链式队列初始化-不带头结点链式队列入队-不带头节点链式队列出队-不带头结点带头结点…...

2024年11月最新 Alfred 5 Powerpack (MACOS)下载
在现代数字化办公中,我们常常被繁杂的任务所包围,而时间的高效利用成为一项核心需求。Alfred 5 Powerpack 是一款专为 macOS 用户打造的高效工作流工具,以其强大的定制化功能和流畅的用户体验,成为众多效率爱好者的首选。 点击链…...

ODBC连接PostgreSQL数据库后,网卡DOWN后,客户端进程阻塞问题解决方法
问题现象:数据库客户端进程数据库连接成功后,再把跟数据库交互的网卡down掉,客户端进程就会阻塞,无法进行其他处理。该问题跟TCP keepalive机制有关。 可以在odbc.ini文件中增加相应的属性来解决,在odbc.ini 增加如下…...
_vscode commit很慢解决方法)
VsCode使用git提交很慢(一直显示在提交)_vscode commit很慢解决方法
VsCode使用git提交很慢(一直显示在提交)_vscode commit很慢...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...
