NewStar CTF week5 Crypto wp
easy_ecc
ecc的模板题,稍加推理就会发现c1=m+c2*k因此做一个减法就行,需要注意的点是c1,c2必须放到ecc里面过一道才能出正确结果
k = 86388708736702446338970388622357740462258632504448854088010402300997950626097
p = 64408890408990977312449920805352688472706861581336743385477748208693864804529
a = 111430905433526442875199303277188510507615671079377406541731212384727808735043
b = 89198454229925288228295769729512965517404638795380570071386449796440992672131
E = EllipticCurve(GF(p),[a,b])
c1 = E([10968743933204598092696133780775439201414778610710138014434989682840359444219,50103014985350991132553587845849427708725164924911977563743169106436852927878] )
c2 = E([16867464324078683910705186791465451317548022113044260821414766837123655851895,35017929439600128416871870160299373917483006878637442291141472473285240957511])
c_left = 15994601655318787407246474983001154806876869424718464381078733967623659362582
c_right = 3289163848384516328785319206783144958342012136997423465408554351179699716569
m=c1-k*c2
print(long_to_bytes(c_left//m[0])+long_to_bytes(c_right//m[1]))没e也能玩
一开始看到dp以为是一个dp泄露题,结果一细看,不是哥们

搞定
RSA?cmd5!
这道题感觉教学意义更重,也是直观的看到了数字签名的过程,flag采用公钥e加密,而m生成的MD5使用私钥d加密,这也就意味着,我们使用公钥e可以解密数字签名,从而验证消息的来源
c = 119084320846787611587774426118526847905825678869032529318497425064970463356147909835330423466179802531093233559613714033492951177656433798856482195873924140269461792479008703758436687940228268475598134411304167494814557384094637387369282900460926092035234233538644197114822992825439656673482850515654334379332
s = 5461514893126669960233658468203682813465911805334274462134892270260355037191167357098405392972668890146716863374229152116784218921275571185229135409696720018765930919309887205786492284716906060670649040459662723215737124829497658722113929054827469554157634284671989682162929417551313954916635460603628116503
[n,e] = [139458221347981983099030378716991183653410063401398496859351212711302933950230621243347114295539950275542983665063430931475751013491128583801570410029527087462464558398730501041018349125941967135719526654701663270142483830687281477000567117071676521061576952568958398421029292366101543468414270793284704549051, 65537]
m0=long_to_bytes(pow(s,e,n))
print(m0)
m0='adm0n12'
flag = 'flag{th1s_1s_my_k3y:' + m0 + '0x' + hashlib.sha256(m0.encode()).hexdigest() + '}'
print(flag)解出md5的值后,随便找个在线网站解密即可
md5在线解密破解,md5解密加密
格格你好棒
进去看脚本很简单,给的信息几乎等于没有,一看就是触及到知识盲区的东西,果断看wp
格密码这部分看了很久,对原理的部分依然不是很清楚,不过至少摸清楚了这类题怎么解决。
附上几个介绍这部分的网址:
【CTF-Crypto】格密码基础(例题较多,非常适合入门!)_ctf crypto-CSDN博客
crypto-从NTRU算法入门格密码 - 先知社区
简单的说,这是一个格密码的NTRU问题,那么这一部分问题怎么解决呢?首先了解它的加密过程
格密码笔记(一)
从公钥生成过程,可以得到hf=g+kp,借此,我们可以构造格,而对于其他题目,可以依据一开始的基础公式构造形如格的式子,关键是理清楚谁是f,谁是g,谁是h。

构造到这里,需要通过Hermite定理检查一下位数,

左边向量v的值是根号下(f**2+g**2),右边n代表维数,一般是二维,det是基的行列式的值
左右两边的bit_length()相差越小,结果越精确,如果相差过大,则构造b=2**x,x根据需要调整。
b1 = gmpy2.iroot(2 * b * p, 2)[0]
print(b1.bit_length()) # 381b2 = gmpy2.iroot(f**2+(b*g)**2, 2)[0]
print(b2.bit_length()) #376
变换的过程其实就是等式两边同时*b,只不过左边乘到了[h,p]这个列向量上形成[h*b,b*p],而右边乘到g上形成b*g,所以最后解密出来的结果也是b*g。
调整完毕之后,就可以根据LLL算法计算最小基,即等式右边的(f,g)
那么看一下这道题的脚本,感受一下
from Crypto.Util.number import *
import random
flag = b'******'
m = bytes_to_long(flag)a = getPrime(1024)
b = getPrime(1536)p = getPrime(512)
q = getPrime(512)
r = random.randint(2**8, 2**9)
assert ((p+2*r) * 3*a + q) % b < 70c = pow(m, 0x10001, p*q)print(f'c =', c)
print(f'a =', a)
print(f'b =', b)
这里有一个断言assert ((p+2*r) * 3*a + q) % b < 70,其实就相当于h=((p+2*r)*3*a+q)%b,再化简,得(p+2*r)*3*a=q-h+kb,我们对比公钥得生成公式:
hf=g+kp
那么其实f就相当于(p+2r),同样,h=3*a,g=q-h,p=b,所以构造矩阵

解出得f=p+2*r,g=q-h,奇怪的是,在这道题里不用Hermite定理调整也能得出正确答案
from Crypto.Util.number import *
import gmpy2
c = 75671328500214475056134178451562126288749723392201857886683373274067151096013132141603734799638338446362190819013087028001291030248155587072037662295281180020447012070607162188511029753418358484745755426924178896079516327814868477319474776976247356213687362358286132623490797882893844885783660230132191533753
a = 99829685822966835958276444400403912618712610766908190376329921929407293564120124118477505585269077089315008380226830398574538050051718929826764449053677947419802792746249036134153510802052121734874555372027104653797402194532536147269634489642315951326590902954822775489385580372064589623985262480894316345817
b = 2384473327543107262477269141248562917518395867365960655318142892515553817531439357316940290934095375085624218120779709239118821966188906173260307431682367028597612973683887401344727494920856592020970209197406324257478251502340099862501536622889923455273016634520507179507645734423860654584092233709560055803703801064153206431244982586989154685048854436858839309457140702847482240801158808592615931654823643778920270174913454238149949865979522520566288822366419746x=2**512
L = Matrix(ZZ,[[1,3*a*x],[0,b*x]])
p,q = L.LLL()[0] # 这里的 [0] 是取其中的最小向量
p,q = abs(p),abs(q)# 爆破 r 和 h
for r in range(2**8,2**9):for h in range(70):pp = p - 2*rqq = q//x + hphi = (pp-1)*(qq-1)if gcd(phi,65537) != 1:continuem = power_mod(c,inverse_mod(65537,phi),pp*qq)if b'flag' in long_to_bytes(m):print(long_to_bytes(m))学以致用
刚进历上一道题的折磨,实在不想看论文了,后面心态调整好了再回来更新
相关文章:

NewStar CTF week5 Crypto wp
easy_ecc ecc的模板题,稍加推理就会发现c1mc2*k因此做一个减法就行,需要注意的点是c1,c2必须放到ecc里面过一道才能出正确结果 k 86388708736702446338970388622357740462258632504448854088010402300997950626097 p 644088904089909773124499208053…...

vue3+antd注册全局v-loading指令
文章目录 1. 创建指令文件2. 全局注册3. 使用 1. 创建指令文件 src/directives 在directives中创建如下文件 src│─directives│ index.ts└─loadingindex.tsindex.vuedirectives/ index.ts export * from ./loadingdirectives/loading/index.ts import { createApp } f…...

初试无监督学习 - K均值聚类算法
文章目录 1. K均值聚类算法概述2. k均值聚类算法演示2.1 准备工作2.2 生成聚类用的样本数据集2.3 初始化KMeans模型对象,并指定类别数量2.4 用样本数据训练模型2.5 用训练好的模型生成预测结果2.6 输出预测结果2.7 可视化预测结果 3. 实战小结 1. K均值聚类算法概述…...

捉虫笔记(七)-再探谁把系统卡住了
捉虫笔记(七)-再探谁把系统卡住 1、内核调试 在实体物理机上,内核调试的第一个门槛就是如何建立调试链接。 这里我选择的建立网络连接进行内核调试。 至于如何建立网络连接后续文章再和大家分享。 2、如何分析 在上一篇文章中,我们…...

【Linux课程学习】:《简易版shell实现和原理》 《哪些命令可以让子进程执行,哪些命令让shell执行(内键命令)?为什么?》
🎁个人主页:我们的五年 🔍系列专栏:Linux课程学习 🌷追光的人,终会万丈光芒 🎉欢迎大家点赞👍评论📝收藏⭐文章 目录 打印命令行提示符(PrintCommandLin…...

2024年11月27日Github流行趋势
项目名称:screenshot-to-code 项目维护者:abi clean99 sweep-ai kachbit vagusX项目介绍:通过上传截图将其转换为整洁的代码(支持HTML/Tailwind/React/Vue)。项目star数:62,429项目fork数:7,614…...

Java中的线程池使用详解
文章目录 Java中的线程池使用详解一、引言二、线程池的创建与使用1、线程池的创建1.1、FixedThreadPool(固定大小线程池)1.2、CachedThreadPool(可缓存线程池)1.3、SingleThreadExecutor(单线程化线程池)1.…...

Redis(概念、IO模型、多路选择算法、安装和启停)
一、概念 关系型数据库是典型的行存储数据库,存在的问题是,按行存储的数据在物理层面占用的是连续存储空间,不适合海量数据存储。 Redis在生产中使用的最多的是用作数据缓存。 服务器先在缓存中查询数据,查到则返回,…...
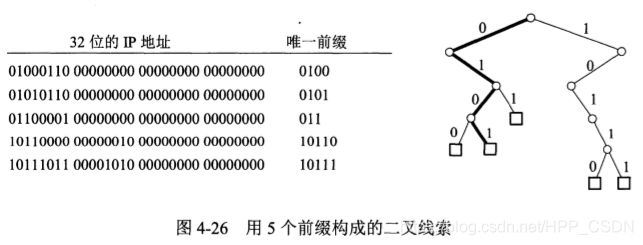
计算机网络 第4章 网络层
计算机网络 (第八版)谢希仁 第 4 章 网络层4.2.2 IP地址**无分类编址CIDR**IP地址的特点 4.2.3 IP地址与MAC地址4.2.4 ARP 地址解析协议4.2.5 IP数据报的格式题目2:IP数据报分片与重组题目:计算IP数据报的首部校验和(不正确未改) …...

Java学习笔记--继承方法的重写介绍,重写方法的注意事项,方法重写的使用场景,super和this
目录 一,方法的重写 二,重写方法的注意事项 三,方法重写的使用场景 四,super和this 1.继承中构造方法的特点 2.super和this的具体使用 super的具体使用 this的具体使用 一,方法的重写 1.概述:子类中有一个和父类…...

高级java每日一道面试题-2024年11月27日-JVM篇-JVM的永久代中会发生垃圾回收么?
如果有遗漏,评论区告诉我进行补充 面试官: JVM的永久代中会发生垃圾回收么? 我回答: 在Java虚拟机(JVM)的历史版本中,确实存在一个称为“永久代”(Permanent Generation, 或者简称PermGen)的内存区域。永久代主要用…...
Spring Boot教程之十: 使用 Spring Boot 实现从数据库动态下拉列表
使用 Spring Boot 实现从数据库动态下拉列表 动态下拉列表(或依赖下拉列表)的概念令人兴奋,但编写起来却颇具挑战性。动态下拉列表意味着一个下拉列表中的值依赖于前一个下拉列表中选择的值。一个简单的例子是三个下拉框,分别显示…...

基于混合ABC和A*算法复现
基于混合ABC和A*算法复现 一、背景介绍二、算法原理(一)A*算法原理(二)人工蜂群算法原理(三)混合ABC和A*算法策略 三、代码实现(一)数据准备(二)关键函数实现…...

狂野飙车8+(Asphalt 8+) for Mac 赛车竞速游戏 安装教程
Mac分享吧 文章目录 狂野飙车8(Asphalt 8) for Mac 赛车竞速游戏软件 效果图展示一、狂野飙车8(Asphalt 8) 赛车竞速游戏 Mac电脑版——v2.1.11️⃣:下载软件2️⃣:安装软件2.1 左侧安装包拖入右侧文件夹中,等待安装完成,运行软件…...
部署介绍)
网络技术-VRRP(虚拟路由冗余协议)部署介绍
一、VRRP的含义 VRRP(Virtual Router Redundancy Protocol,虚拟路由冗余协议)是一种高度可靠的路由器备用协议,用于在局域网内部提供路由器冗余。 其部署方式主要是通过多个路由器组成一个虚拟路由器组,通过协议选…...

C语言解决空瓶换水问题:高效算法与实现
标题:C语言解决空瓶换水问题:高效算法与实现 一、问题描述 在一个饮料促销活动中,你可以通过空瓶换水的方式免费获得更多的水:3个空瓶可以换1瓶水。喝完这瓶水后,空瓶会再次变为空瓶。假设你最初拥有一定数量的空瓶&a…...

day2全局注册
全局注册代码: //文件核心作用:导入App.vue,基于App.vue创建结构渲染index.htmlimport Vue from vue import App from ./App.vue //编写导入的代码,往代码的顶部编写(规范) import HmButton from ./components/Hm-But…...

鸿蒙多线程应用-taskPool
并发模型 并发模型是用来实现不同应用场景中并发任务的编程模型,常见的并发模型分为基于内存共享的并发模型和基于消息通信的并发模型。 Actor并发模型作为基于消息通信并发模型的典型代表,不需要开发者去面对锁带来的一系列复杂偶发的问题,同…...

【失败经验】将算法模型封装为安卓应用
背景:不懂安卓开发,希望能使用大模型编码完成安卓应用生成,调用算法模型进行预测。 模型准备: pip方案安装pcnn; 然后需要将pytorch训练完成的算法模型保存为torchscript模型,然后使用pcnn转换为ncnn的模…...

ABAP OOALV模板
自用模板,可能存在问题 一、主程序 *&---------------------------------------------------------------------* *& Report ZVIA_OO_ALV *&---------------------------------------------------------------------* REPORT ZVIA_OO_ALV.INCLUDE ZVI…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...
