动手学深度学习10.5. 多头注意力-笔记练习(PyTorch)
本节课程地址:多头注意力代码_哔哩哔哩_bilibili
本节教材地址:10.5. 多头注意力 — 动手学深度学习 2.0.0 documentation
本节开源代码:...>d2l-zh>pytorch>chapter_multilayer-perceptrons>multihead-attention.ipynb
多头注意力
在实践中,当给定相同的查询、键和值的集合时, 我们希望模型可以基于相同的注意力机制学习到不同的行为, 然后将不同的行为作为知识组合起来, 捕获序列内各种范围的依赖关系 (例如,短距离依赖和长距离依赖关系)。 因此,允许注意力机制组合使用查询、键和值的不同 子空间表示(representation subspaces)可能是有益的。
为此,与其只使用单独一个注意力汇聚, 我们可以用独立学习得到的 组不同的 线性投影(linear projections)来变换查询、键和值。 然后,这
组变换后的查询、键和值将并行地送到注意力汇聚中。 最后,将这
个注意力汇聚的输出拼接在一起, 并且通过另一个可以学习的线性投影进行变换, 以产生最终输出。 这种设计被称为多头注意力(multihead attention) (="https://zh.d2l.ai/chapter_references/zreferences.html#id174">Vaswaniet al., 2017)。 对于
个注意力汇聚输出,每一个注意力汇聚都被称作一个头(head)。 图10.5.1 展示了使用全连接层来实现可学习的线性变换的多头注意力。

模型
在实现多头注意力之前,让我们用数学语言将这个模型形式化地描述出来。 给定查询 、 键
和 值
, 每个注意力头
(
)的计算方法为:
其中,可学习的参数包括 、
和
, 以及代表注意力汇聚的函数
。
可以是 10.3节 中的 加性注意力和缩放点积注意力。 多头注意力的输出需要经过另一个线性转换, 它对应着
个头连结后的结果,因此其可学习参数是
:
基于这种设计,每个头都可能会关注输入的不同部分, 可以表示比简单加权平均值更复杂的函数。
import math
import torch
from torch import nn
from d2l import torch as d2l实现
在实现过程中通常[选择缩放点积注意力作为每一个注意力头]。 为了避免计算代价和参数代价的大幅增长, 我们设定 。 值得注意的是,如果将查询、键和值的线性变换的输出数量设置为
, 则可以并行计算
个头。 在下面的实现中,
是通过参数
num_hiddens指定的。
#@save
class MultiHeadAttention(nn.Module):"""多头注意力"""def __init__(self, key_size, query_size, value_size, num_hiddens,num_heads, dropout, bias=False, **kwargs):super(MultiHeadAttention, self).__init__(**kwargs)self.num_heads = num_headsself.attention = d2l.DotProductAttention(dropout)self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)def forward(self, queries, keys, values, valid_lens):# queries,keys,values的形状:# (batch_size,查询或者“键-值”对的个数,num_hiddens)# valid_lens 的形状:# (batch_size,)或(batch_size,查询的个数)# 经过变换后,输出的queries,keys,values 的形状:# (batch_size*num_heads,查询或者“键-值”对的个数,# num_hiddens/num_heads)queries = transpose_qkv(self.W_q(queries), self.num_heads)keys = transpose_qkv(self.W_k(keys), self.num_heads)values = transpose_qkv(self.W_v(values), self.num_heads)if valid_lens is not None:# 在轴0,将第一项(标量或者矢量)复制num_heads次,# 然后如此复制第二项,然后诸如此类。valid_lens = torch.repeat_interleave(valid_lens, repeats=self.num_heads, dim=0)# output的形状:(batch_size*num_heads,查询的个数,# num_hiddens/num_heads)output = self.attention(queries, keys, values, valid_lens)# output_concat的形状:(batch_size,查询的个数,num_hiddens)output_concat = transpose_output(output, self.num_heads)return self.W_o(output_concat)为了能够[使多个头并行计算], 上面的MultiHeadAttention类将使用下面定义的两个转置函数。 具体来说,transpose_output函数反转了transpose_qkv函数的操作。
#@save
def transpose_qkv(X, num_heads):"""为了多注意力头的并行计算而变换形状"""# 输入X的形状:(batch_size,查询或者“键-值”对的个数,num_hiddens)# 输出X的形状:(batch_size,查询或者“键-值”对的个数,num_heads,# num_hiddens/num_heads)X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)# 输出X的形状:(batch_size,num_heads,查询或者“键-值”对的个数,# num_hiddens/num_heads)X = X.permute(0, 2, 1, 3)# 最终输出的形状:(batch_size*num_heads,查询或者“键-值”对的个数,# num_hiddens/num_heads)return X.reshape(-1, X.shape[2], X.shape[3])#@save
def transpose_output(X, num_heads):"""逆转transpose_qkv函数的操作"""# 输入X的形状:(batch_size*num_heads,查询或者“键-值”对的个数,num_hiddens/num_heads)# 输出X的形状:(batch_size,num_heads,查询或者“键-值”对的个数,num_hiddens/num_heads)X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])# 输出X的形状:(batch_size,查询或者“键-值”对的个数,num_heads,num_hiddens/num_heads)X = X.permute(0, 2, 1, 3)# 最终输出的形状:((batch_size,查询或者“键-值”对的个数,num_hiddens)return X.reshape(X.shape[0], X.shape[1], -1)下面使用键和值相同的小例子来[测试]我们编写的MultiHeadAttention类。 多头注意力输出的形状是(batch_size,num_queries,num_hiddens)。
num_hiddens, num_heads = 100, 5
attention = MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,num_hiddens, num_heads, 0.5)
attention.eval()
MultiHeadAttention((attention): DotProductAttention((dropout): Dropout(p=0.5, inplace=False))(W_q): Linear(in_features=100, out_features=100, bias=False)(W_k): Linear(in_features=100, out_features=100, bias=False)(W_v): Linear(in_features=100, out_features=100, bias=False)(W_o): Linear(in_features=100, out_features=100, bias=False)
)
batch_size, num_queries = 2, 4
num_kvpairs, valid_lens = 6, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
Y = torch.ones((batch_size, num_kvpairs, num_hiddens))
attention(X, Y, Y, valid_lens).shape
torch.Size([2, 4, 100])小结
- 多头注意力融合了来自于多个注意力汇聚的不同知识,这些知识的不同来源于相同的查询、键和值的不同的子空间表示。
- 基于适当的张量操作,可以实现多头注意力的并行计算。
练习
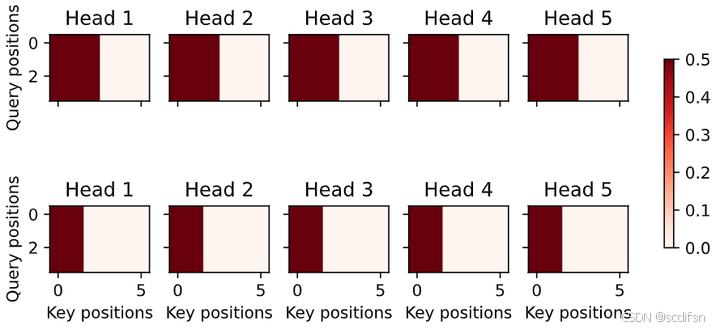
- 分别可视化这个实验中的多个头的注意力权重。
解:
代码如下:
attention.attention.attention_weights.shape
# (batch_size*num_heads,查询的个数,“键-值”对的个数)输出结果:
torch.Size([10, 4, 6])
d2l.show_heatmaps(attention.attention.attention_weights.reshape((2,5,4,6)), xlabel='Key positions', ylabel='Query positions', titles=['Head %d' % i for i in range(1, 6)],figsize=(8, 3.5))输出结果:
2. 假设有一个完成训练的基于多头注意力的模型,现在希望修剪最不重要的注意力头以提高预测速度。如何设计实验来衡量注意力头的重要性呢?
解:
首先定义评判注意力头重要性的指标,比如预测速度等;
然后采用单一变量法,修剪某一个头或某几个头的组合,重新训练模型,并在验证集上评估重要性指标的变化; 最后根据重要性指标的变化,判断最不重要的一个或几个注意力头,并修剪。
相关文章:

动手学深度学习10.5. 多头注意力-笔记练习(PyTorch)
本节课程地址:多头注意力代码_哔哩哔哩_bilibili 本节教材地址:10.5. 多头注意力 — 动手学深度学习 2.0.0 documentation 本节开源代码:...>d2l-zh>pytorch>chapter_multilayer-perceptrons>multihead-attention.ipynb 多头注…...
)
13 设计模式之外观模式(家庭影院案例)
一、什么是外观模式? 1.定义 在日常生活中,许多人喜欢通过遥控器来控制家中的电视、音响、DVD 播放器等设备。虽然这些设备各自独立工作,但遥控器提供了一个简洁的界面,让用户可以轻松地操作多个设备。而这一设计理念正是 外观模…...

单片机学习笔记 12. 定时/计数器_定时
更多单片机学习笔记:单片机学习笔记 1. 点亮一个LED灯单片机学习笔记 2. LED灯闪烁单片机学习笔记 3. LED灯流水灯单片机学习笔记 4. 蜂鸣器滴~滴~滴~单片机学习笔记 5. 数码管静态显示单片机学习笔记 6. 数码管动态显示单片机学习笔记 7. 独立键盘单片机学习笔记 8…...

Web安全基础实践
实践目标 (1)理解常用网络攻击技术的基本原理。(2)Webgoat实践下相关实验。 WebGoat WebGoat是由著名的OWASP负责维护的一个漏洞百出的J2EE Web应用程序,这些漏洞并非程序中的bug,而是故意设计用来讲授We…...

Zookeeper集群数据是如何同步的?
大家好,我是锋哥。今天分享关于【Zookeeper集群数据是如何同步的?】面试题。希望对大家有帮助; Zookeeper集群数据是如何同步的? 1000道 互联网大厂Java工程师 精选面试题-Java资源分享网 Zookeeper集群中的数据同步是通过一种称为ZAB(Zo…...
SpringCloud框架学习(第六部分:Sentinel实现熔断与限流)
目录 十四、SpringCloud Alibaba Sentinel实现熔断与限流 1.简介 2.作用 3.下载安装 4.微服务 8401 整合 Sentinel 入门案例 5.流控规则 (1)基本介绍 (2)流控模式 Ⅰ. 直接 Ⅱ. 关联 Ⅲ. 链路 (3࿰…...
动态规划-----路径问题
动态规划-----路径问题 下降最小路径和1:状态表示2:状态转移方程3 初始化4 填表顺序5 返回值6 代码实现 总结: 下降最小路径和 1:状态表示 假设:用dp[i][j]表示:到达[i,j]的最小路径 2:状态转…...

Rust循环引用与多线程并发
循环引用与自引用 循环引用的概念 循环引用指的是两个或多个对象之间相互持有对方的引用。在 Rust 中,由于所有权和生命周期的严格约束,直接创建循环引用通常会导致编译失败。例如: // 错误的循环引用示例 struct Node {next: Option<B…...
东方隐侠网安瞭望台第8期
谷歌应用商店贷款应用中的 SpyLoan 恶意软件影响 800 万安卓用户 迈克菲实验室的新研究发现,谷歌应用商店中有十多个恶意安卓应用被下载量总计超过 800 万次,这些应用包含名为 SpyLoan 的恶意软件。安全研究员费尔南多・鲁伊斯上周发布的分析报告称&…...
底部导航栏新增功能按键
场景需求: 在底部导航栏添加power案件,单击息屏,长按 关机 如下实现图 借此需求,需要掌握技能: 底部导航栏如何实现新增、修改、删除底部导航栏流程对底部导航栏部分样式如何修改。 比如放不下、顺序排列、坑点如…...
C++ 之弦上舞:string 类与多样字符串操作的优雅旋律
string 类的重要性及与 C 语言字符串对比 在 C 语言中,字符串是以 \0 结尾的字符集合,操作字符串需借助 C 标准库的 str 系列函数,但这些函数与字符串分离,不符合 OOP 思想,且底层空间管理易出错。而在 C 中࿰…...
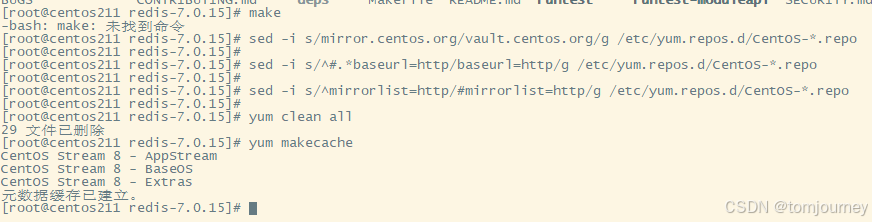
centos8:Could not resolve host: mirrorlist.centos.org
【1】错误消息: [rootcentos211 redis-7.0.15]# yum update CentOS Stream 8 - AppStream …...

Linux 定时任务 命令解释 定时任务格式详解
目录 时间命令 修改时间和日期 定时任务格式 定时任务执行 查看定时任务进程 重启定时任务 时间命令 #查看时间 [rootlocalhost ~]# date 2021年 07月 23日 星期五 14:38:19 CST --------------------------------------- [rootlocalhost ~]# date %F 2021-07-23 -----…...
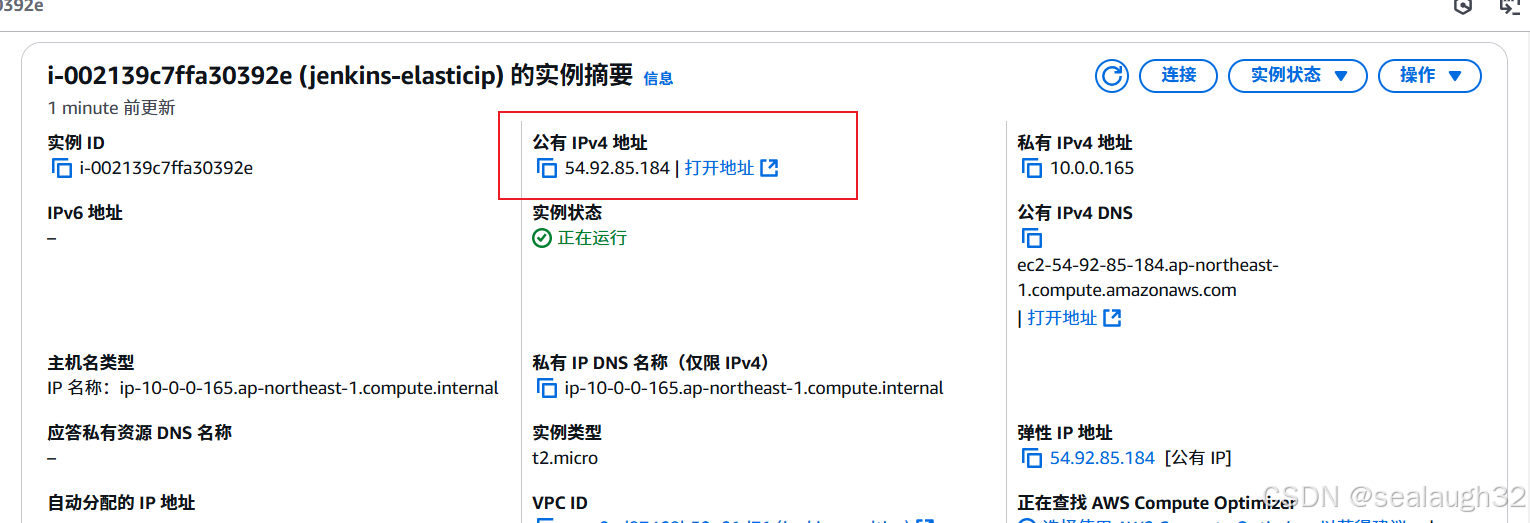
aws(学习笔记第十五课) 如何从灾难中恢复(recover)
aws(学习笔记第十五课) 如何从灾难中恢复 学习内容: 使用CloudWatch对服务器进行监视与恢复区域(region),可用区(available zone)和子网(subnet)使用自动扩展(AutoScalingGroup) 1. 使用CloudWatch对服务器进行监视与恢复 整体架构 这里模拟Jenkins Se…...
github webhooks 实现网站自动更新
本文目录 Github Webhooks 介绍Webhooks 工作原理配置与验证应用云服务器通过 Webhook 自动部署网站实现复制私钥编写 webhook 接口Github 仓库配置 webhook以服务的形式运行 app.py Github Webhooks 介绍 Webhooks是GitHub提供的一种通知方式,当GitHub上发生特定事…...

【C语言】递归的内存占用过程
递归 递归是函数调用自身的一种编程技术。在C语言中,递归的实现会占用内存栈(Call Stack),每次递归调用都会在栈上分配一个新的 “栈帧(Stack Frame)”,用于存储本次调用的函数局部变量、返回地…...

365天深度学习训练营-第P6周:VGG-16算法-Pytorch实现人脸识别
🍨 本文为🔗365天深度学习训练营中的学习记录博客🍖 原作者:K同学啊 文为「365天深度学习训练营」内部文章 参考本文所写记录性文章,请在文章开头带上「👉声明」 🍺要求: 保存训练过…...

企业AI助理在数据分析与决策中扮演的角色
在当今这个数据驱动的时代,企业每天都需要处理和分析大量的数据,以支持其业务决策。然而,面对如此庞大的数据量,传统的数据分析方法已经显得力不从心。幸运的是,随着人工智能(AI)技术的不断发展…...

洛谷 B2029:大象喝水 ← 圆柱体体积
【题目来源】https://www.luogu.com.cn/problem/B2029【题目描述】 一只大象口渴了,要喝 20 升水才能解渴,但现在只有一个深 h 厘米,底面半径为 r 厘米的小圆桶 (h 和 r 都是整数)。问大象至少要喝多少桶水才会解渴。 …...

go每日一题:mock打桩、defer、recovery、panic的调用顺序
题目一:单元测试中使用—打桩 打桩概念:使用A替换 原函数B,那么A就是打桩函数打桩原理:运行时,通过一个包,将内存中函数的地址替换为桩函数的地址打桩操作:利用Patch()函…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
