深入理解AVL树:结构、旋转及C++实现
1. AVL树的概念
什么是AVL树?
AVL树是一种自平衡的二叉搜索树,其发明者是Adelson-Velsky和Landis,因此得名“AVL”。AVL树是首个自平衡二叉搜索树,通过对树的平衡因子进行控制,确保任何节点的左右子树高度差最多为1,从而保证树的高度为对数级别,即 O(logN)O(\log N)O(logN)。
在AVL树中,插入、删除和查找的时间复杂度都可以保持在 O(logN)O(\log N)O(logN),这使得AVL树在需要频繁查询数据的应用场景中非常高效。

AVL树的平衡因子
每个节点有一个平衡因子(Balance Factor),定义如下:
- 平衡因子 = 右子树高度 - 左子树高度
- 对于任何节点,平衡因子的可能取值为 -1、0、1。
AVL树通过保持所有节点的平衡因子在上述范围内,确保了树的平衡。这个平衡性减少了树的高度,从而提高了数据查找效率。
为什么要平衡?
普通的二叉搜索树(BST)在最坏情况下会退化成链表。例如,按照递增顺序插入节点会使树的所有节点都集中在右边,导致高度等于节点数,查找复杂度为 O(N)O(N)O(N)。AVL树通过自动维护平衡性,避免了这种情况,确保所有操作的复杂度始终为对数级别。
2. AVL树的实现
2.1 AVL树的结构
AVL树的节点结构非常类似于普通的二叉树节点,不过增加了一个字段用于存储平衡因子。以下是AVL树节点的结构定义:
template<class K, class V>
struct AVLTreeNode {pair<K, V> _kv; // 键值对AVLTreeNode<K, V>* _left; // 左子节点AVLTreeNode<K, V>* _right; // 右子节点AVLTreeNode<K, V>* _parent; // 父节点int _bf; // 平衡因子(balance factor)AVLTreeNode(const pair<K, V>& kv): _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0) {}
};
2.2 AVL树的插入
AVL树的插入操作和普通二叉搜索树的插入类似,但需要额外的步骤来确保树的平衡。如果插入新节点后某些节点失衡,我们需要通过旋转来恢复平衡。
插入步骤概述
- 按普通BST的规则插入:首先将节点按照二叉搜索树的规则插入。
- 更新平衡因子:从插入节点开始,向上遍历其祖先节点,更新每个节点的平衡因子。
- 检查并旋转平衡树:如果某节点的平衡因子变为2或-2,说明该节点失衡。此时需要通过旋转操作恢复平衡。
插入代码实现
以下是AVL树插入节点的代码实现:
bool Insert(const pair<K, V>& kv) {if (_root == nullptr) {_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur) {if (cur->_kv.first < kv.first) {parent = cur;cur = cur->_right;} else if (cur->_kv.first > kv.first) {parent = cur;cur = cur->_left;} else {return false; // 不允许插入重复的键值}}cur = new Node(kv);if (parent->_kv.first < kv.first) {parent->_right = cur;} else {parent->_left = cur;}cur->_parent = parent;// 更新平衡因子while (parent) {if (cur == parent->_left) {parent->_bf--;} else {parent->_bf++;}if (parent->_bf == 0) {break; // 更新结束,无需继续} else if (parent->_bf == 1 || parent->_bf == -1) {cur = parent;parent = parent->_parent; // 继续向上更新} else if (parent->_bf == 2 || parent->_bf == -2) {// 失衡,需要进行旋转操作Balance(parent);break;} else {assert(false); // 不应存在其他情况}}return true;
}
2.3 旋转操作
当AVL树失去平衡时,通过旋转操作来恢复平衡。旋转的类型分为四种:右单旋、左单旋、左右双旋和右左双旋。每种旋转操作都有其适用场景和具体的实现。
旋转的类型
- 右单旋(Right Rotation):用于修正左子树过高的情况。

- 左单旋(Left Rotation):用于修正右子树过高的情况。

- 左右双旋(Left-Right Rotation):用于修正节点插入在左子树的右侧,导致子树高度增加的情况。

- 右左双旋(Right-Left Rotation):用于修正节点插入在右子树的左侧,导致子树高度增加的情况。
右单旋实现
右单旋用于修正某个节点的左子树过高的情况。以下是右单旋的代码:
void RotateR(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR) {subLR->_parent = parent;}Node* parentParent = parent->_parent;subL->_right = parent;parent->_parent = subL;if (parentParent == nullptr) {_root = subL;subL->_parent = nullptr;} else {if (parent == parentParent->_left) {parentParent->_left = subL;} else {parentParent->_right = subL;}subL->_parent = parentParent;}// 更新平衡因子parent->_bf = subL->_bf = 0;
}
左单旋实现
左单旋用于修正某个节点的右子树过高的情况。以下是左单旋的代码实现:
void RotateL(Node* parent) {Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL) {subRL->_parent = parent;}Node* parentParent = parent->_parent;subR->_left = parent;parent->_parent = subR;if (parentParent == nullptr) {_root = subR;subR->_parent = nullptr;} else {if (parent == parentParent->_left) {parentParent->_left = subR;} else {parentParent->_right = subR;}subR->_parent = parentParent;}// 更新平衡因子parent->_bf = subR->_bf = 0;
}
左右双旋和右左双旋实现
当子树的高度增加发生在左右子树中的某一侧时,单次旋转无法恢复平衡,需要进行双次旋转。
- 左右双旋(Left-Right Rotation):首先对左子树进行左旋,再对祖先节点进行右旋。
- 右左双旋(Right-Left Rotation):首先对右子树进行右旋,再对祖先节点进行左旋。
void RotateLR(Node* parent) {RotateL(parent->_left);RotateR(parent);
}void RotateRL(Node* parent) {RotateR(parent->_right);RotateL(parent);
}
2.4 AVL树的查找操作
AVL树的查找操作和普通二叉搜索树类似,由于AVL树保持平衡,查找操作的时间复杂度始终为 O(logN)O(\log N)O(logN)。以下是查找的代码实现:
Node* Find(const K& key) {Node* cur = _root;while (cur) {if (cur->_kv.first < key) {cur = cur->_right;} else if (cur->_kv.first > key) {cur = cur->_left;} else {return cur; // 找到节点}}return nullptr; // 节点未找到
}
2.5 AVL树的平衡性检测(深入扩展)
平衡性检测的目标
AVL树的平衡性检测旨在验证每个节点是否满足AVL树的平衡要求,即每个节点的左右子树高度差绝对值不超过1,同时保证每个节点的平衡因子正确反映左右子树的高度差。
为了验证AVL树的平衡性,检测的目标有两个:
- 验证左右子树的高度差是否满足AVL条件。
- 验证每个节点的平衡因子是否正确反映了其子树的高度差。
平衡性检测的挑战
在进行平衡性检测时,我们面临两个主要挑战:
- 递归遍历的深度与效率问题:对树的每个节点,我们需要递归计算其子树的高度,较高的递归深度可能导致性能下降。
- 同步验证平衡因子:在递归计算高度的过程中,我们需要同时验证每个节点的平衡因子是否正确。
平衡性检测的代码实现
以下是用于检测AVL树平衡性和正确性的代码:
int _Height(Node* root) {if (root == nullptr) return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return max(leftHeight, rightHeight) + 1;
}bool _IsBalanceTree(Node* root) {if (root == nullptr) return true;// 计算左右子树的高度int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);int diff = rightHeight - leftHeight;// 检查高度差是否符合AVL条件if (abs(diff) > 1) {cout << root->_kv.first << " 高度差异常: 左高=" << leftHeight << ", 右高=" << rightHeight << endl;return false;}// 检查平衡因子是否正确if (root->_bf != diff) {cout << root->_kv.first << " 平衡因子异常: 期望=" << diff << ", 实际=" << root->_bf << endl;return false;}// 递归检测左右子树是否平衡return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}
代码说明
- 高度计算:
_Height函数用于计算节点的高度,递归遍历每个节点的左右子树,返回最大的高度加1。 - 平衡性验证:
_IsBalanceTree函数用于检测树的平衡性。它首先计算每个节点的左右子树高度差,然后检查其平衡因子是否符合AVL树的定义。 - 详细输出:为了帮助调试,函数在检测到异常时输出详细的信息,包括节点的键值、高度差和不匹配的平衡因子值。
平衡性检测的改进:优化高度计算
在上述实现中,_Height 函数被重复调用多次,可能会导致效率低下。特别是在平衡性检测过程中,每次都要重新递归计算子树的高度。我们可以通过以下优化来提升效率。
同时计算高度与检测平衡性
我们可以通过一次递归同时计算高度和检测平衡性,避免重复的高度计算。以下是改进后的代码:
// 新的平衡检测函数,返回子树的高度并同时检测是否平衡
int _CheckBalance(Node* root, bool& isBalanced) {if (root == nullptr) return 0;int leftHeight = _CheckBalance(root->_left, isBalanced);int rightHeight = _CheckBalance(root->_right, isBalanced);// 如果在递归过程中已经发现不平衡,直接返回if (!isBalanced) return 0;// 计算当前节点的高度差int diff = rightHeight - leftHeight;// 检查高度差是否符合AVL条件if (abs(diff) > 1) {cout << "节点 " << root->_kv.first << " 高度差异常: 左高=" << leftHeight << ", 右高=" << rightHeight << endl;isBalanced = false;}// 检查平衡因子是否正确if (root->_bf != diff) {cout << "节点 " << root->_kv.first << " 平衡因子异常: 期望=" << diff << ", 实际=" << root->_bf << endl;isBalanced = false;}// 返回子树的高度return max(leftHeight, rightHeight) + 1;
}// 检测整棵树是否平衡的入口函数
bool IsBalanceTree() {bool isBalanced = true;_CheckBalance(_root, isBalanced);return isBalanced;
}
代码改进点
-
高度计算与平衡检测结合:
- 在新的实现中,
_CheckBalance函数同时执行高度计算和平衡性检测。 - 递归调用返回子树的高度,同时检查每个节点的平衡性,从而减少了重复的递归操作。
- 在新的实现中,
-
标志位:
- 通过
bool& isBalanced参数作为标志位,当发现树中有不平衡的节点时,将其设为false,并立即终止后续的递归。 - 这样可以避免不必要的计算,提高检测的整体效率。
- 通过
-
减少重复计算:
- 与之前的版本相比,新的实现避免了重复的高度计算,每个节点只需一次遍历即可完成高度计算和平衡性检测。
进阶:检查树的平衡因子及其更新的正确性
除了检测平衡性之外,还可以扩展检测模块,进一步确保AVL树中的每个节点的平衡因子在插入和旋转操作之后都得到了正确更新。以下是检测平衡因子的代码。
验证每个节点的平衡因子
在进行插入、删除等操作后,平衡因子必须保持正确更新。我们可以通过递归遍历整棵树来验证每个节点的平衡因子是否准确反映其子树的高度差。
bool ValidateBalanceFactors(Node* root) {if (root == nullptr) return true;// 递归获取左右子树高度int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);int expectedBF = rightHeight - leftHeight;// 检查平衡因子是否正确if (root->_bf != expectedBF) {cout << "节点 " << root->_kv.first << " 的平衡因子不正确。应为 " << expectedBF << ",实际为 " << root->_bf << endl;return false;}// 递归验证左右子树的平衡因子return ValidateBalanceFactors(root->_left) && ValidateBalanceFactors(root->_right);
}
代码说明
ValidateBalanceFactors函数遍历整个树,检查每个节点的平衡因子是否与其左右子树的高度差匹配。- 这种检测可以在每次插入、删除或旋转之后调用,以确保树在操作后没有出现错误的平衡因子。
- 如果发现平衡因子不正确,程序会输出详细的错误信息,包括节点的键值、应有的平衡因子和当前存储的平衡因子。
平衡性检测的应用场景
- 单元测试:在开发AVL树时,可以在每次插入、删除或旋转操作后调用平衡性检测函数,作为单元测试的一部分。
- 调试与验证:通过详细的错误信息输出,开发者可以快速定位到问题节点,从而帮助调试和验证代码的正确性。
- 性能优化:平衡性检测不仅可以帮助验证算法的正确性,还可以用于评估在不同数据分布和操作顺序下,AVL树的性能表现是否达到了预期。
3. AVL树的应用场景及优势
AVL树适合应用于需要高效查找的场景中,例如数据库中的索引结构、缓存系统中的快速查找等。相比于普通的二叉搜索树,AVL树保证了每次操作的时间复杂度为 O(logN)O(\log N)O(logN),特别适合频繁插入和删除的应用。
4. C++实现的完整代码示例
以下是一个AVL树完整的C++实现代码示例,结合了插入、旋转、查找和检测的实现。
template<class K, class V>
class AVLTree {typedef AVLTreeNode<K, V> Node;public:bool Insert(const pair<K, V>& kv);Node* Find(const K& key);void InOrder() const;bool IsBalanceTree();private:Node* _root = nullptr;void RotateR(Node* parent);void RotateL(Node* parent);void RotateLR(Node* parent);void RotateRL(Node* parent);
};
在实际编程中,使用AVL树可以保证数据的有序性,同时保证在最坏情况下依然具有高效的时间复杂度,非常适合需要高频率动态数据维护的场景。
5. 结论
AVL树是一种经典的自平衡二叉搜索树,通过引入平衡因子和旋转操作,保持了树的平衡性,确保了插入、删除和查找操作的高效性。通过学习AVL树,我们可以深入理解数据结构的自平衡机制,以及如何在二叉树中保持最优的性能。
希望通过这篇博客,大家对AVL树的概念、实现和用途有更深的了解。如果你有任何疑问或者想了解更多相关内容,欢迎随时交流。
相关文章:

深入理解AVL树:结构、旋转及C++实现
1. AVL树的概念 什么是AVL树? AVL树是一种自平衡的二叉搜索树,其发明者是Adelson-Velsky和Landis,因此得名“AVL”。AVL树是首个自平衡二叉搜索树,通过对树的平衡因子进行控制,确保任何节点的左右子树高度差最多为1&…...
R24-11)
AUTOSAR AP 汽车API知识点总结(Automotive API )R24-11
汽车API知识点总结 一、背景与目标 背景:智能互联汽车正逐步依赖远程诊断、软件更新等功能以确保行驶安全,并且用户已习惯于通过智能设备中的应用程序控制连接设备。虽然AUTOSAR标准支持车辆软件的可更新性,但尚未提供将AUTOSAR应用产生的数据和功能安全可靠地暴露给非AUTO…...
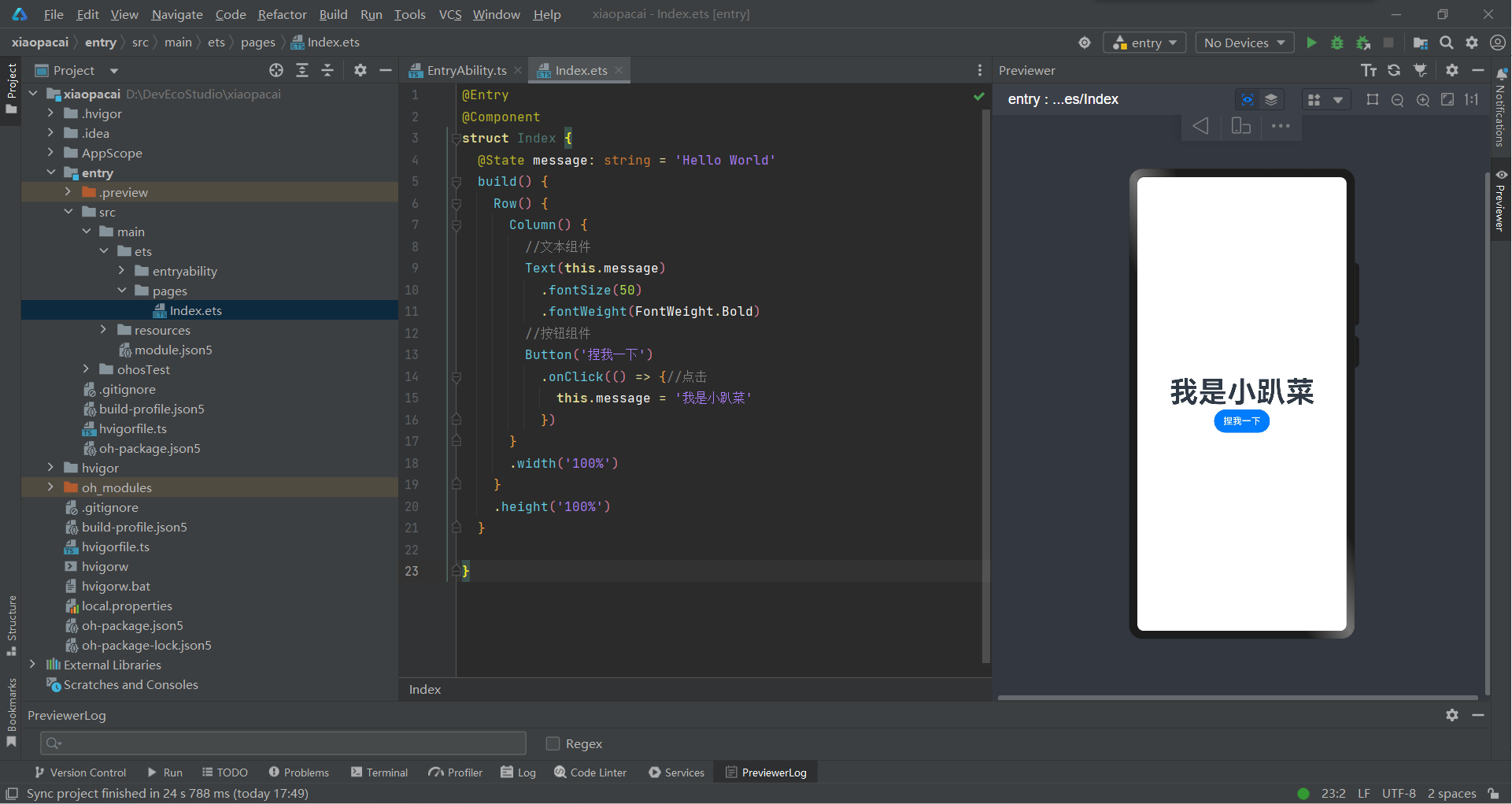
【HarmonyOS开发】超详细的ArkTS入门
安装DevEco Studio和新建项目就不多说了,可以移步官网 就可以把他们拆成这几个部分了,如果看不懂可以暂时忽略下面冒号后面的内容 装饰器:用于装饰类、结构、方法以及变量,并赋予其特殊的含义。如上述示例中Entry、Component和St…...
SpringBoot3整合Sentinel-nacos持久化策略)
Springboot(五十一)SpringBoot3整合Sentinel-nacos持久化策略
上文中我记录了在Springboot项目中链接sentinel-dashboard使用限流规则的全过程。 但是呢,有一个小小的问题,我重启了一下我本地的sentinel-dashboard服务,然后,我之前创建的所有的流控规则都没了…… 这……好像有点不合理啊,咱就不能找地儿存储一下?你这一重启就没了,…...

[go-redis]客户端的创建与配置说明
创建redis client 使用go-redis库进行创建redis客户端比较简单,只需要调用redis.NewClient接口创建一个客户端 redis.NewClient(&redis.Options{Addr: "127.0.0.1:6379",Password: "",DB: 0, })NewClient接口只接收一个参数red…...
Qt入门7——Qt事件
目录 1. Qt事件介绍: 2. 事件的处理 示例1:鼠标进入(enterEvent)与离开事件(leaveEvent) 示例2:鼠标点击事件(mousePressEvent) 示例3:鼠标移动事件(mouseMoveEvent) 3. 按键事件 4. 定时器 5. 窗口事件 1. Qt事件介绍&a…...
)
CTF之密码学(仓颉编码)
一、仓颉码(用于建立中文索引) 定义与目标: 仓颉码是为了建立中文的索引观念而设计的一种编码方式。其主要目标是方便对中文资料或程式进行索引功能的处理。 工作原理: 仓颉码的索引以ASCII的字符码为基准,但在内部会转…...

面向人工智能安全的多维应对策略
• 制定并实施人工智能伦理框架 国家和行业层面需建立AI伦理原则,将其融入研发与应用中,强化科研人员的伦理培训,推动全球AI伦理框架的制定。 • 加强可信数字内容体系建设 构建可信的互联网内容体系以应对深度伪造带来的安全威胁ÿ…...

考研英语翻译与大小作文
名词动化词 1 持有 harbor2 2 反映 mirror 3 缩短 bridge 4 使用 harness 5 掩饰 mask/veil 6 修改 tailor 7 汇集 pool 8 控制 curb 9 想象 picture 10 激发 trigger 拉丁…...

视频监控汇聚平台Liveweb视频安防监控实时视频监控系统操作方案
Liveweb国标GB28181视频平台是一种基于国标GB/T28181协议的安防视频流媒体能力平台。它支持多种视频功能,包括实时监控直播、录像、检索与回看、语音对讲、云存储、告警以及平台级联等功能。该平台部署简单、可扩展性强,支持全终端、全平台分发接入的视频…...

算法第一弹-----双指针
目录 1.移动零 2.复写零 3.快乐数 4.盛水最多的容器 5.有效三角形的个数 6.查找总价值为目标值的两个商品 7.三数之和 8.四数之和 双指针通常是指在解决问题时,同时使用两个指针(变量,常用来指向数组、链表等数据结构中的元素位置&am…...
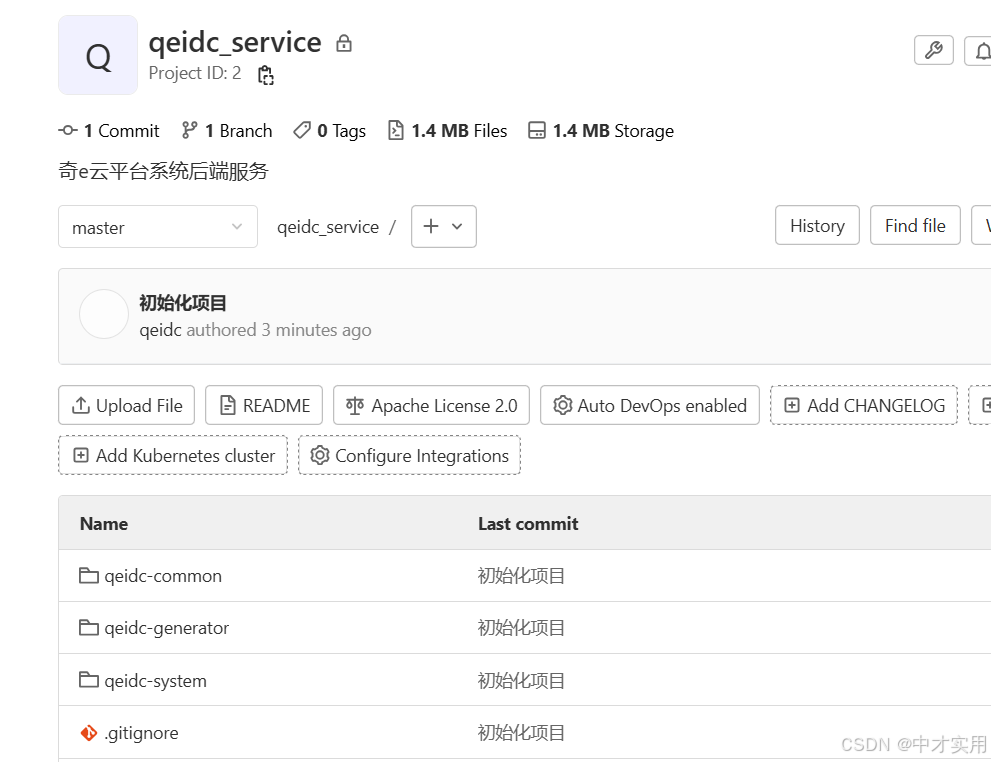
linux环境GitLab服务部署安装及使用
一、GitLab介绍 GitLab是利用Ruby onRails一个开源的版本管理系统,实现一个自托管的Git项目仓库,可通过Web界面进行访问公开的或者私人项目。 二、GitLab安装 1、先安装相关依赖 yum -y install policycoreutils openssh-server openssh-clients postf…...

MotorCAD:定子绕组中的趋肤效应和邻近效应损耗
MotorCAD 有助于减少定子绕组中的集肤效应和邻近效应损失,优化电动机性能。 了解集肤和邻近效应损失 集肤效应:交流电场在导体中感应出电流回路,增加了中心的磁通链路,导致该位置的电抗更高,结果是电流在表面附近流动…...

R语言机器学习论文(二):数据准备
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍加载R包数据下载导入数据一、数据描述二、数据预处理(一)修改元素名称(二)剔除无关变量(三)缺失值检查(四)重复值检查(五)异常值检查三、描述性统计(一)连续变量数据情…...

FFmpeg:强大的音视频处理工具指南
FFmpeg:强大的音视频处理工具指南 1. FFmpeg简介2. 核心特性2.1 基础功能2.2 支持的格式和编解码器 3. 主要组件3.1 命令行工具3.2 开发库 4. 最新发展5. 安装指南5.1 Windows系统安装5.1.1 直接下载可执行文件5.1.2 使用包管理器安装 5.2 Linux系统安装5.2.1 Ubunt…...

NiFi-从部署到开发(图文详解)
NiFi简介 Apache NiFi 是一款强大的开源数据集成工具,旨在简化数据流的管理、传输和自动化。它提供了直观的用户界面和可视化工具,使用户能够轻松设计、控制和监控复杂的数据流程,NiFi 具备强大的扩展性和可靠性,可用于处理海量数…...
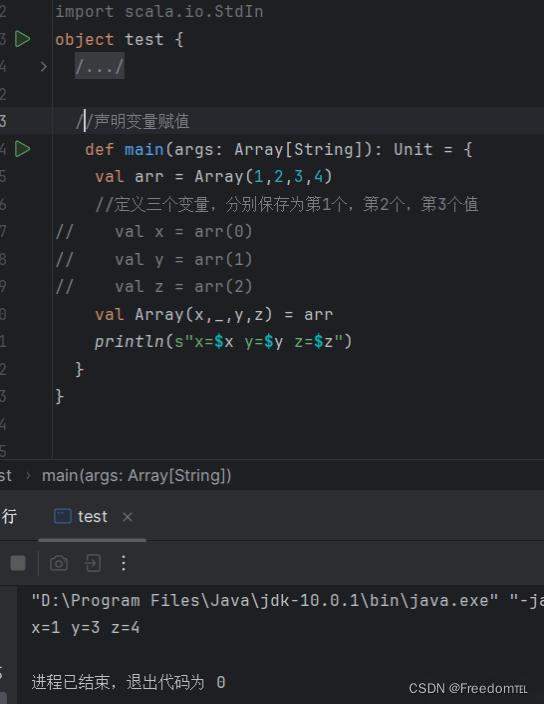
Scala的条件匹配
条件匹配 在 Scala 中,条件匹配主要通过match表达式来实现,它类似于其他语言中的switch语句,但功能更强。 基本语法:match表达式通常与case关键字一起使用。语法格式如下: 输入一段数字,判断属于那个范围…...

如何手搓一个智能激光逗猫棒
背景 最近家里的猫胖了,所以我就想做个逗猫棒。找了一圈市场上的智能逗猫棒,运行轨迹比较单一,互动性不足。 轨迹单一,活动范围有限 而我希望后续可以结合人工智能物联网,通过摄像头来捕捉猫的位置,让小…...

leetcode LCP 开幕式焰火
LCP 44. 开幕式焰火 - 力扣(LeetCode) 「力扣挑战赛」开幕式开始了,空中绽放了一颗二叉树形的巨型焰火。 给定一棵二叉树 root 代表焰火,节点值表示巨型焰火这一位置的颜色种类。请帮小扣计算巨型焰火有多少种不同的颜色。 示例…...
使用GDI对象绘制UI时需要注意的若干细节问题总结
目录 1、一个bitmap不能同时被选进两个dc中 2、CreateCompatibleDC和CreateCompatibleBitmap要使用同一个dc作为参数 3、不能删除已经被选入DC中的GDI对象 4、使用完的GDI对象,要将之释放掉,否则会导致GDI对象泄漏 5、CreateCompatibleBitmap返回错…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

