力扣-图论-2【算法学习day.52】
前言
###我做这类文章一个重要的目的还是给正在学习的大家提供方向和记录学习过程(例如想要掌握基础用法,该刷哪些题?)我的解析也不会做的非常详细,只会提供思路和一些关键点,力扣上的大佬们的题解质量是非常非常高滴!!!
习题
1.所有可能的路径
题目链接:797. 所有可能的路径 - 力扣(LeetCode)
题面:
分析:简单的dfs
代码:
class Solution {List<List<Integer>> ans = new ArrayList<>();int n;int[][] graph;public List<List<Integer>> allPathsSourceTarget(int[][] graph) {List<Integer> list = new ArrayList<>();n = graph.length;this.graph = graph;int[] flag = new int[n];list.add(0);recursion(list,0,flag);return ans;}public void recursion(List<Integer> list,int x,int[] flag){// System.out.println(x);if(x==(n-1)){// System.out.println(1);ans.add(new ArrayList<>(list));}int[] arr = graph[x];int m = arr.length;for(int i = 0;i<m;i++){if(flag[arr[i]]==0){list.add(arr[i]);flag[arr[i]] = 1;recursion(list,arr[i],flag);flag[arr[i]] = 0;list.remove(list.size()-1);}} }
}2.钥匙和房间
题目链接:841. 钥匙和房间 - 力扣(LeetCode)
题面:
代码:
class Solution {int n;int[] have;int count;int[] flag;List<List<Integer>> rooms;public boolean canVisitAllRooms(List<List<Integer>> rooms) {this.rooms = rooms;n = rooms.size();List<Integer> list = rooms.get(0);have = new int[n];flag = new int[n];flag[0] = 1;count = n-1;have[0] = 1;for(int a:list){if(have[a]==0)count--;have[a] = 1;}recursion(have);System.out.println(count);return count==0?true:false;}public void recursion(int[] have){int blog = 0;for(int i = 0;i<n;i++){if(have[i]==1&&flag[i]==0){flag[i] = 1;List<Integer> list = rooms.get(i);for(int a:list){if(have[a]==0)count--;have[a] = 1;}blog = 1;}}if(blog==1)recursion(have);}
}后言
上面是力扣图论专题,下一篇是其他的习题,希望有所帮助,一同进步,共勉!
相关文章:

力扣-图论-2【算法学习day.52】
前言 ###我做这类文章一个重要的目的还是给正在学习的大家提供方向和记录学习过程(例如想要掌握基础用法,该刷哪些题?)我的解析也不会做的非常详细,只会提供思路和一些关键点,力扣上的大佬们的题解质量是非…...

MySQL如何区分幻读和不可重复读
在MySQL中,幻读和不可重复读都是并发事务中可能出现的问题,但它们的表现和原因略有不同。 不可重复读 (Non-Repeatable Read) 不可重复读是指在同一个事务内,多次读取同一行数据时,可能会得到不同的结果。这种情况发生在一个事务…...

界面控件Syncfusion Essential Studio®现在已完全支持 .NET 9
Syncfusion Essential Studio现在完全支持 .NET 9,可最新版本2024 Volume 3 版本中使用!通过此更新,Blazor、.NET MAUI、WPF、WinForms、WinUI和ASP.NET Core 平台中的 Syncfusion 组件以及文档处理库已准备好让您利用 .NET 9 中的最新功能。…...

openEuler安装lsb_release
lsb_release是linux下查看发行版信息用的工具 lsb_release只是一个小程序,它的包名并不是lsb_release lsb_release其实是红帽的一个项目,其名为redhat-lsb 我们的lsb_release就是其中的一部分,更准确的说是redhat-lsb-core 从网站࿱…...

统计数字字符个数
统计数字字符个数 C语言实现C实现Java实现Python实现 💐The Begin💐点点关注,收藏不迷路💐 输入一行字符,统计出其中数字字符的个数。 输入 一行字符串,总长度不超过255。 输出 出为1行,输出…...

44页PDF | 信息化战略规划标准框架方法论与实施方法(限免下载)
一、前言 这份报告详细介绍了企业信息化战略规划的标准框架、方法论以及实施方法,强调了信息化规划应以业务战略和IT战略为驱动力,通过构筑企业架构(EA)来连接长期战略和信息化建设。报告提出了信息化规划原则,探讨了…...

计算机网络期末复习-part1-概述
1、互联网的组成 互联网由两大块组成。 1、边沿部分:由所有连接在互联网上的主机组成,是用户直接使用的部分。 2、核心部分,由大量网络和路由器组成,为边缘部分提供服务。 2、数据传送阶段的三种交换方式的主要特点 1、电路交…...

A1228 php+Mysql旅游供需平台的设计与实现 导游接单 旅游订单 旅游分享网站 thinkphp框架 源码 配置 文档 全套资料
旅游供需平台 1.项目描述2. 开发背景与意义3.项目功能4.界面展示5.源码获取 1.项目描述 随着社会经济的快速发展,生活水平的提高,人们对旅游的需求日益增强,因此,为给用户提供一个便利的查看导游信息,进行导游招募的平…...

RabbitMQ消息可靠性保证机制5--消息幂等性处理
RabbitMQ层面有实现“去重机制”来保证“恰好一次”吗?答案是没并没有,而且现在主流的消息中间件都没有实现。 一般解决重复消息的办法是:在消费端让我们消费消息操作具有幂等性。 幂等性问题并不是消息系统独有,而是࿰…...

Claude3.5如何使用?
Claude 3.5 Sonnet,性能直接吊打了 GPT-4o,甚至价格还更便宜。网友们纷纷展开实测,有人表示自己一半的工作已经可以由它替代了!而最让人惊喜的新功能,莫过于 Artifacts 了。 就在昨天,Anthropic 深夜发布了…...

力扣刷题TOP101:14.BM16 删除有序链表中重复的元素-II
目录: 目的 思路 复杂度 记忆秘诀 python代码 目的 1→1→2→3→3 删除重复后变成2。 思路 这个任务是删除链表里重复的节点包含本身。可以看成是一个抽奖活动的系统升级。某人通过多种方式报名(节点不同),后台数据检测到这些…...

解决github网络慢的问题
前言 本文采用替换host的方式来加速github的git请求,主要我自己用来备份的懒人方式,不然每次都要手动修改hosts文件,skrskrskr… 一、获取到可用的ip 先到这个网站查询到低延迟的ip 站长工具:https://ping.chinaz.com/ 第2步&…...

docker及docker exec命令学习笔记
docker exec 是一个常用的 Docker 命令,允许你在已经运行的容器中执行命令或启动新的进程。以下是详细介绍和常见用法: 基本语法 docker exec [OPTIONS] CONTAINER COMMAND [ARG...]参数详解 1. CONTAINER指定目标容器的名字或容器 ID。可以通过以下命…...

linux环境宝塔服务部署安装及介绍
一、简介 宝塔面板是一款服务器管理软件,支持windows和linux系统,可以通过Web端轻松管理服务器,提升运维效率。例如:创建管理网站、FTP、数据库,拥有可视化文件管理器,可视化软件管理器,可视化C…...
概念与应用: 中英双语)
充分统计量(Sufficient Statistic)概念与应用: 中英双语
充分统计量:概念与应用 在统计学中,充分统计量(Sufficient Statistic) 是一个核心概念。它是从样本中计算得出的函数,能够完整且无损地表征样本中与分布参数相关的信息。在参数估计中,充分统计量能够帮助我…...
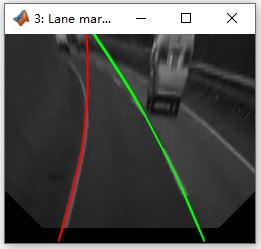
基于Matlab计算机视觉的车道线识别与前车检测系统研究
随着自动驾驶技术的发展,车道线识别和前车检测成为智能驾驶系统中的核心技术之一。本实训报告围绕基于计算机视觉的车道线识别与前车检测系统展开,旨在通过处理交通视频数据,实时检测车辆所在车道及其与前车的相对位置,从而为车道…...

模糊测试中常见的10种变异mutation策略
1. 引入 基于变异策略的模糊测试,有两个重点: (1)seed:种子,初始的合法输入序列。 (2)mutation:对已经存在的输入序列,进行微调。 所以,mutatio…...
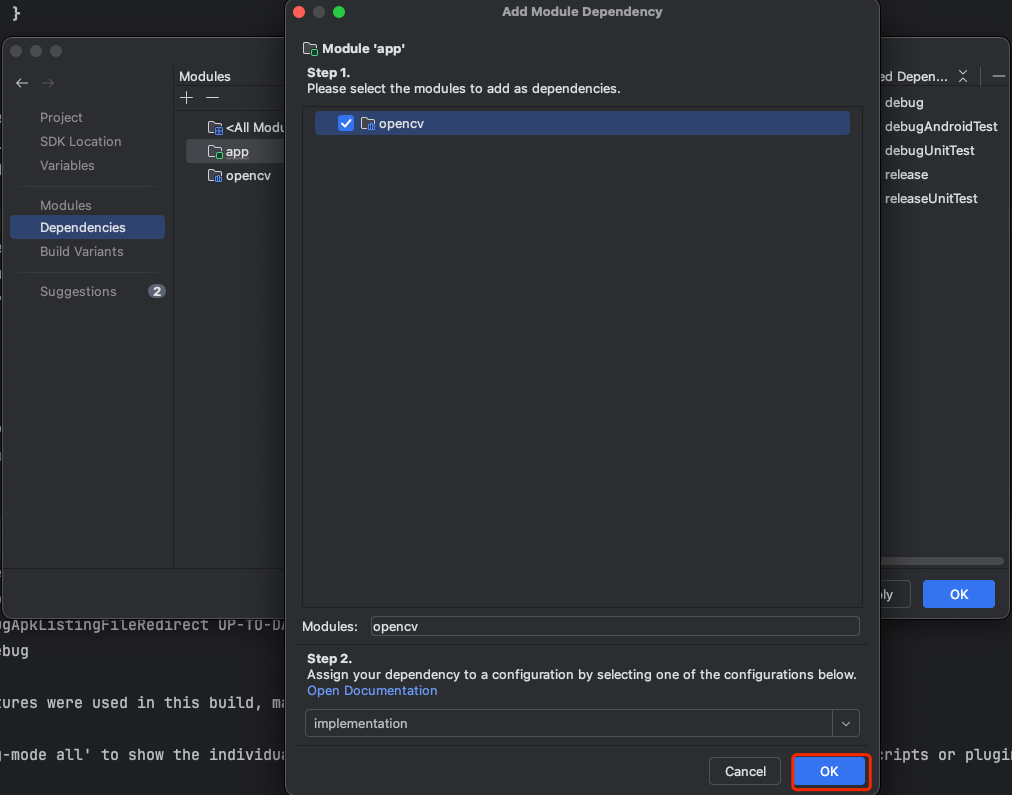
opencv-android编译遇到的相关问题处理
1、opencv-android sdk下载 下载地址:https://opencv.org/releases/ 下载安卓SDK即可 2、解压下载好的SDK 3、导入opencv的SDK到安卓项目中 导入步骤在/OpenCV-android-sdk/sdk/build.gradle文件的注释中写的非常详细,大家可安装官方给出的步骤导入。…...

把 py脚本生成windows 可执行的文件
1 确保生成的exe文件,不会立即退出 input("Please input any key to exit!")2 安装 PyInstaller 确保已经安装了 PyInstaller。可以使用 pip 来安装它: pip install pyinstaller3 执行命令 这里的 --onefile 选项表示将所有依赖项打包到一…...

云计算的发展历史与未来展望
云计算的起源与发展 云计算的概念最早可以追溯到20世纪60年代,当时的计算机科学家约翰麦卡锡(John McCarthy)提出了“按需提供计算能力”的构想。尽管这一理念在当时的技术条件下无法实现,但为云计算的未来发展奠定了理论基础。 …...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...
