充分统计量(Sufficient Statistic)概念与应用: 中英双语
充分统计量:概念与应用
在统计学中,充分统计量(Sufficient Statistic) 是一个核心概念。它是从样本中计算得出的函数,能够完整且无损地表征样本中与分布参数相关的信息。在参数估计中,充分统计量能够帮助我们提取必要的统计信息,从而实现更高效的推断。
本文将从充分统计量的定义出发,结合指数族分布的例子,深入探讨这一概念及其在统计推断中的重要性。
1. 充分统计量的定义
设 ( X = { x 1 , x 2 , … , x n } X = \{x_1, x_2, \dots, x_n\} X={x1,x2,…,xn} ) 是来自分布 ( p ( x ∣ θ ) p(x|\theta) p(x∣θ) ) 的样本,其中 ( θ \theta θ ) 是分布的参数。统计量 ( T ( X ) T(X) T(X) ) 被称为关于参数 ( θ \theta θ ) 的充分统计量,如果满足因子分解定理(Factorization Theorem):
p ( X ∣ θ ) = h ( X ) g ( T ( X ) , θ ) , p(X|\theta) = h(X) g(T(X), \theta), p(X∣θ)=h(X)g(T(X),θ),
其中:
- ( T ( X ) T(X) T(X) ) 是样本的函数,即统计量;
- ( h ( X ) h(X) h(X) ) 是与 ( θ \theta θ ) 无关的函数;
- ( g ( T ( X ) , θ ) g(T(X), \theta) g(T(X),θ) ) 是 ( T ( X ) T(X) T(X) ) 与 ( θ \theta θ ) 的联合函数。
直观解释:充分统计量 ( T ( X ) T(X) T(X) ) 能够提取样本中关于参数 ( θ \theta θ ) 的全部信息,( h ( X ) h(X) h(X) ) 则捕捉了样本中与 ( θ \theta θ ) 无关的其他信息。
2. 充分统计量的意义
假设我们已经计算了充分统计量 ( T ( X ) T(X) T(X) ),则原始样本 ( X X X ) 中的其他信息对于 ( θ \theta θ ) 的估计是冗余的。也就是说,利用 ( T ( X ) T(X) T(X) ) 进行推断,与直接使用整个样本 ( X X X ) 的效果是等价的。
例如,在正态分布 ( X ∼ N ( μ , σ 2 ) X \sim \mathcal{N}(\mu, \sigma^2) X∼N(μ,σ2) ) 中:
- 样本均值 ( x ˉ = 1 n ∑ i = 1 n x i \bar{x} = \frac{1}{n} \sum_{i=1}^n x_i xˉ=n1∑i=1nxi ) 是 ( μ \mu μ ) 的充分统计量;
- 样本方差 ( s 2 = 1 n ∑ i = 1 n ( x i − x ˉ ) 2 s^2 = \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2 s2=n1∑i=1n(xi−xˉ)2 ) 是 ( σ 2 \sigma^2 σ2 ) 的充分统计量。
3. 指数族分布与充分统计量
指数族分布是统计学中一类重要的分布形式,其概率密度函数(或质量函数)可以统一表示为:如果读者对指数族分布的概率密度函数的形式有疑问,请参考笔者的另一篇文章 指数族分布(Exponential Family of Distributions)的两种形式及其区别
p ( x ∣ θ ) = h ( x ) exp ( η ( θ ) T t ( x ) − A ( θ ) ) , p(x|\theta) = h(x) \exp\left(\eta(\theta)^T t(x) - A(\theta)\right), p(x∣θ)=h(x)exp(η(θ)Tt(x)−A(θ)),
其中:
- ( η ( θ ) \eta(\theta) η(θ) ) 是参数 ( θ \theta θ ) 的自然参数;
- ( t ( x ) t(x) t(x) ) 是样本的充分统计量;
- ( A ( θ ) A(\theta) A(θ) ) 是规范化因子,保证分布的积分为 1;
- ( h ( x ) h(x) h(x) ) 是与参数无关的测度函数。
3.1 常见的指数族分布例子
正态分布(均值已知,方差未知)
概率密度函数:
p ( x ∣ μ , σ 2 ) = 1 2 π σ 2 exp ( − ( x − μ ) 2 2 σ 2 ) . p(x|\mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right). p(x∣μ,σ2)=2πσ21exp(−2σ2(x−μ)2).
写成指数族形式:
p ( x ∣ μ , σ 2 ) = exp ( − 1 2 σ 2 x 2 + μ σ 2 x − μ 2 2 σ 2 − 1 2 ln ( 2 π σ 2 ) ) . p(x|\mu, \sigma^2) = \exp\left(-\frac{1}{2\sigma^2} x^2 + \frac{\mu}{\sigma^2} x - \frac{\mu^2}{2\sigma^2} - \frac{1}{2} \ln(2\pi\sigma^2)\right). p(x∣μ,σ2)=exp(−2σ21x2+σ2μx−2σ2μ2−21ln(2πσ2)).
充分统计量为:
t ( x ) = { x , x 2 } . t(x) = \{x, x^2\}. t(x)={x,x2}.
泊松分布
概率质量函数:
p ( x ∣ λ ) = λ x e − λ x ! , x = 0 , 1 , 2 , … p(x|\lambda) = \frac{\lambda^x e^{-\lambda}}{x!}, \quad x = 0, 1, 2, \dots p(x∣λ)=x!λxe−λ,x=0,1,2,…
写成指数族形式:
p ( x ∣ λ ) = exp ( x ln λ − λ − ln x ! ) . p(x|\lambda) = \exp\left(x \ln \lambda - \lambda - \ln x!\right). p(x∣λ)=exp(xlnλ−λ−lnx!).
充分统计量为:
t ( x ) = x . t(x) = x. t(x)=x.
二项分布
概率质量函数:
p ( x ∣ n , p ) = ( n x ) p x ( 1 − p ) n − x , x = 0 , 1 , … , n . p(x|n, p) = \binom{n}{x} p^x (1-p)^{n-x}, \quad x = 0, 1, \dots, n. p(x∣n,p)=(xn)px(1−p)n−x,x=0,1,…,n.
写成指数族形式:
p ( x ∣ n , p ) = exp ( x ln p 1 − p + n ln ( 1 − p ) + ln ( n x ) ) . p(x|n, p) = \exp\left(x \ln \frac{p}{1-p} + n \ln (1-p) + \ln \binom{n}{x}\right). p(x∣n,p)=exp(xln1−pp+nln(1−p)+ln(xn)).
充分统计量为:
t ( x ) = x . t(x) = x. t(x)=x.
4. 应用场景
4.1 参数估计
充分统计量极大地简化了参数估计的过程。例如,在最大似然估计(MLE)中,充分统计量允许我们直接基于 ( T ( X ) T(X) T(X) ) 构建似然函数,而无需处理整个样本。
4.2 数据压缩
充分统计量将数据从高维样本 ( X X X ) 压缩为低维统计量 ( T ( X ) T(X) T(X) ),但仍然保留了关于参数 ( θ \theta θ ) 的全部信息。这对于大数据分析尤为重要。
4.3 贝叶斯推断
在贝叶斯框架中,充分统计量可以简化后验分布的计算,因为 ( p ( θ ∣ X ) ∝ p ( T ( X ) ∣ θ ) p ( θ ) p(\theta|X) \propto p(T(X)|\theta)p(\theta) p(θ∣X)∝p(T(X)∣θ)p(θ) )。
5. 总结
充分统计量是统计推断中的关键工具,能够高效提取样本中关于分布参数的信息。通过指数族分布的形式化,我们不仅能够清晰地识别充分统计量,还能理解其在不同分布中的表现形式。充分统计量在参数估计、数据压缩和贝叶斯推断中的广泛应用,进一步凸显了其重要性。
读者在学习时,可以从正态分布、泊松分布等常见的指数族分布入手,尝试推导其充分统计量,以加深对这一概念的理解。
Sufficient Statistic: Concept and Applications
In statistics, the concept of sufficient statistic plays a fundamental role. A sufficient statistic is a function of a dataset that captures all the information about a parameter of interest contained within the data. By leveraging sufficient statistics, we can efficiently perform parameter inference without processing the entire dataset.
This article introduces sufficient statistics, their mathematical definition, and their relevance in statistical inference. We will illustrate the concept with examples from exponential family distributions, along with detailed mathematical formulations.
1. Definition of Sufficient Statistic
Let ( X = { x 1 , x 2 , … , x n } X = \{x_1, x_2, \dots, x_n\} X={x1,x2,…,xn} ) be a sample drawn from a probability distribution ( p ( x ∣ θ p(x|\theta p(x∣θ) ), where ( θ \theta θ ) is the parameter of interest. A statistic ( T ( X ) T(X) T(X) ) is called a sufficient statistic for ( θ \theta θ ) if it satisfies the factorization theorem:
p ( X ∣ θ ) = h ( X ) g ( T ( X ) , θ ) , p(X|\theta) = h(X) \, g(T(X), \theta), p(X∣θ)=h(X)g(T(X),θ),
where:
- ( T ( X ) T(X) T(X) ) is the statistic (a function of the data);
- ( h ( X ) h(X) h(X) ) is a function independent of ( θ \theta θ );
- ( g ( T ( X ) , θ ) g(T(X), \theta) g(T(X),θ) ) depends only on ( T ( X ) T(X) T(X) ) and ( θ \theta θ ).
Intuition
A sufficient statistic ( T ( X ) T(X) T(X) ) extracts all the information about ( θ \theta θ ) from the dataset ( X X X ). Once ( T ( X ) T(X) T(X) ) is computed, the original dataset ( X X X ) provides no additional value for parameter estimation.
2. Importance of Sufficient Statistics
-
Efficient Parameter Estimation
Once the sufficient statistic ( T ( X ) T(X) T(X) ) is computed, we can perform inference on ( θ \theta θ ) without using the entire dataset. This simplifies calculations, especially for large datasets. -
Data Compression
A sufficient statistic reduces the dimensionality of the data while retaining all relevant information about ( θ \theta θ ). For example, instead of using a large dataset, we only need ( T ( X ) T(X) T(X) ), which is often a low-dimensional vector. -
Bayesian Inference
In Bayesian statistics, the posterior distribution ( p ( θ ∣ X ) p(\theta|X) p(θ∣X) ) depends only on ( T ( X ) T(X) T(X) ). This simplifies the computation of posterior distributions.
3. Exponential Family and Sufficient Statistics
The exponential family of distributions provides a convenient framework for identifying sufficient statistics. A probability distribution belongs to the exponential family if it can be expressed as:
p ( x ∣ θ ) = h ( x ) exp ( η ( θ ) T t ( x ) − A ( θ ) ) , p(x|\theta) = h(x) \exp\left(\eta(\theta)^T t(x) - A(\theta)\right), p(x∣θ)=h(x)exp(η(θ)Tt(x)−A(θ)),
where:
- ( η ( θ ) \eta(\theta) η(θ) ) is the natural parameter;
- ( t ( x ) t(x) t(x) ) is the sufficient statistic;
- ( A ( θ ) A(\theta) A(θ)) is the log-partition function, ensuring normalization;
- ( h ( x ) h(x) h(x) ) is a base measure independent of ( θ \theta θ ).
3.1 Examples of Exponential Family Distributions
Normal Distribution (( μ \mu μ ) known, ( σ 2 \sigma^2 σ2 ) unknown)
Probability density function:
p ( x ∣ σ 2 ) = 1 2 π σ 2 exp ( − ( x − μ ) 2 2 σ 2 ) . p(x|\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right). p(x∣σ2)=2πσ21exp(−2σ2(x−μ)2).
Rewritten in exponential family form:
p ( x ∣ σ 2 ) = exp ( − 1 2 σ 2 x 2 + μ σ 2 x − μ 2 2 σ 2 − 1 2 ln ( 2 π σ 2 ) ) . p(x|\sigma^2) = \exp\left(-\frac{1}{2\sigma^2}x^2 + \frac{\mu}{\sigma^2}x - \frac{\mu^2}{2\sigma^2} - \frac{1}{2}\ln(2\pi\sigma^2)\right). p(x∣σ2)=exp(−2σ21x2+σ2μx−2σ2μ2−21ln(2πσ2)).
The sufficient statistic is:
t ( x ) = { x , x 2 } . t(x) = \{x, x^2\}. t(x)={x,x2}.
Poisson Distribution
Probability mass function:
p ( x ∣ λ ) = λ x e − λ x ! , x = 0 , 1 , 2 , … p(x|\lambda) = \frac{\lambda^x e^{-\lambda}}{x!}, \quad x = 0, 1, 2, \dots p(x∣λ)=x!λxe−λ,x=0,1,2,…
Rewritten in exponential family form:
p ( x ∣ λ ) = exp ( x ln λ − λ − ln x ! ) . p(x|\lambda) = \exp\left(x \ln \lambda - \lambda - \ln x!\right). p(x∣λ)=exp(xlnλ−λ−lnx!).
The sufficient statistic is:
t ( x ) = x . t(x) = x. t(x)=x.
Binomial Distribution
Probability mass function:
p ( x ∣ n , p ) = ( n x ) p x ( 1 − p ) n − x , x = 0 , 1 , … , n . p(x|n, p) = \binom{n}{x} p^x (1-p)^{n-x}, \quad x = 0, 1, \dots, n. p(x∣n,p)=(xn)px(1−p)n−x,x=0,1,…,n.
Rewritten in exponential family form:
p ( x ∣ n , p ) = exp ( x ln p 1 − p + n ln ( 1 − p ) + ln ( n x ) ) . p(x|n, p) = \exp\left(x \ln \frac{p}{1-p} + n \ln (1-p) + \ln \binom{n}{x}\right). p(x∣n,p)=exp(xln1−pp+nln(1−p)+ln(xn)).
The sufficient statistic is:
t ( x ) = x . t(x) = x. t(x)=x.
4. Applications of Sufficient Statistics
4.1 Maximum Likelihood Estimation (MLE)
The likelihood function for parameter ( θ \theta θ ) can be written in terms of the sufficient statistic ( T ( X ) T(X) T(X) ). This simplifies the optimization process in MLE, reducing computational complexity.
For example, for the Poisson distribution, the MLE for ( λ \lambda λ ) is:
λ ^ = ∑ i = 1 n x i n , \hat{\lambda} = \frac{\sum_{i=1}^n x_i}{n}, λ^=n∑i=1nxi,
where ( T ( X ) = ∑ i = 1 n x i T(X) = \sum_{i=1}^n x_i T(X)=∑i=1nxi ).
4.2 Bayesian Inference
In Bayesian inference, the posterior distribution depends only on ( T ( X ) T(X) T(X) ):
p ( θ ∣ X ) ∝ p ( T ( X ) ∣ θ ) p ( θ ) . p(\theta|X) \propto p(T(X)|\theta)p(\theta). p(θ∣X)∝p(T(X)∣θ)p(θ).
This makes the computation of posterior distributions more tractable, especially in conjugate prior settings.
4.3 Data Summarization
Sufficient statistics compress data into a smaller, sufficient representation. For instance, in large-scale data applications, computing sufficient statistics instead of storing entire datasets saves storage and computational resources.
5. Summary
Sufficient statistics are a cornerstone of statistical inference, enabling efficient parameter estimation and data summarization. By focusing on the exponential family, we can better understand how sufficient statistics operate in various common distributions, such as the normal, Poisson, and binomial distributions.
Understanding and utilizing sufficient statistics not only simplifies complex statistical procedures but also offers practical advantages in data analysis, particularly in settings with large datasets or complex Bayesian models. Readers are encouraged to explore further by deriving sufficient statistics for different distributions and applying them to real-world problems.
相关文章:
概念与应用: 中英双语)
充分统计量(Sufficient Statistic)概念与应用: 中英双语
充分统计量:概念与应用 在统计学中,充分统计量(Sufficient Statistic) 是一个核心概念。它是从样本中计算得出的函数,能够完整且无损地表征样本中与分布参数相关的信息。在参数估计中,充分统计量能够帮助我…...
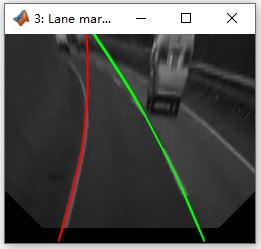
基于Matlab计算机视觉的车道线识别与前车检测系统研究
随着自动驾驶技术的发展,车道线识别和前车检测成为智能驾驶系统中的核心技术之一。本实训报告围绕基于计算机视觉的车道线识别与前车检测系统展开,旨在通过处理交通视频数据,实时检测车辆所在车道及其与前车的相对位置,从而为车道…...

模糊测试中常见的10种变异mutation策略
1. 引入 基于变异策略的模糊测试,有两个重点: (1)seed:种子,初始的合法输入序列。 (2)mutation:对已经存在的输入序列,进行微调。 所以,mutatio…...
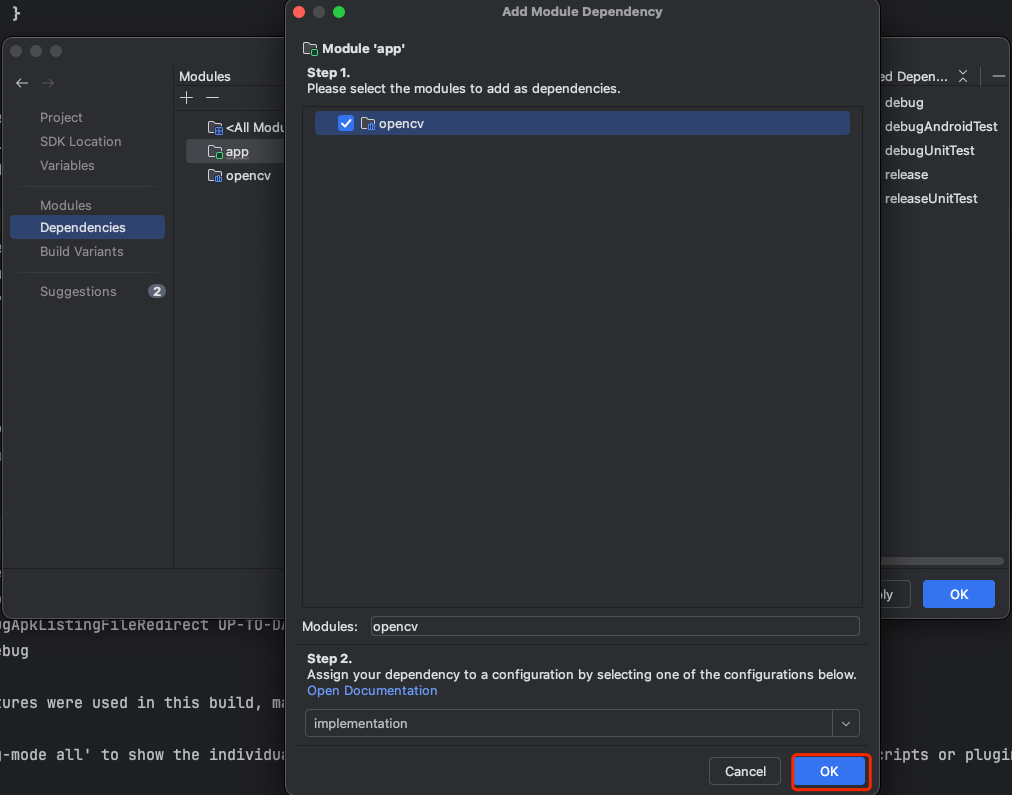
opencv-android编译遇到的相关问题处理
1、opencv-android sdk下载 下载地址:https://opencv.org/releases/ 下载安卓SDK即可 2、解压下载好的SDK 3、导入opencv的SDK到安卓项目中 导入步骤在/OpenCV-android-sdk/sdk/build.gradle文件的注释中写的非常详细,大家可安装官方给出的步骤导入。…...

把 py脚本生成windows 可执行的文件
1 确保生成的exe文件,不会立即退出 input("Please input any key to exit!")2 安装 PyInstaller 确保已经安装了 PyInstaller。可以使用 pip 来安装它: pip install pyinstaller3 执行命令 这里的 --onefile 选项表示将所有依赖项打包到一…...

云计算的发展历史与未来展望
云计算的起源与发展 云计算的概念最早可以追溯到20世纪60年代,当时的计算机科学家约翰麦卡锡(John McCarthy)提出了“按需提供计算能力”的构想。尽管这一理念在当时的技术条件下无法实现,但为云计算的未来发展奠定了理论基础。 …...

基于飞腾S2500处理器的全国产加固服务器
近日,西安康德航测电子科技有限公司凭借其深厚的行业底蕴和创新精神,正式推出了基于飞腾S2500处理器的全国产加固服务器。这一产品的问世,不仅标志着我国在信息技术领域的自立自强迈出了坚实的一步,更以其卓越的性能、坚固的设计和…...
gitlab-cicd部署安装与具体操作
一、安装 本例中是用安装包直接在ubuntu下安装的,也可以用docker镜像。 curl -LJO https://gitlab-runner-downloads.s3.amazonaws.com/latest/rpm/gitlab-runner_amd64.rpmrpm -i gitlab-runner_amd64.rpm 安装runner后,需要跟在runner所在服务器安装…...

2022高等代数上【南昌大学】
2022 高等代数 证明: p ( x ) p(x) p(x) 是不可约多项式的充要条件是对任意的多项式 f ( x ) , g ( x ) f(x), g(x) f(x),g(x),若 p ( x ) ∣ f ( x ) g ( x ) p(x) \mid f(x)g(x) p(x)∣f(x)g(x),则有 p ( x ) ∣ f ( x ) p(x) \mid f(x) p(x)∣f(x) 或 p ( x ) ∣ g (…...
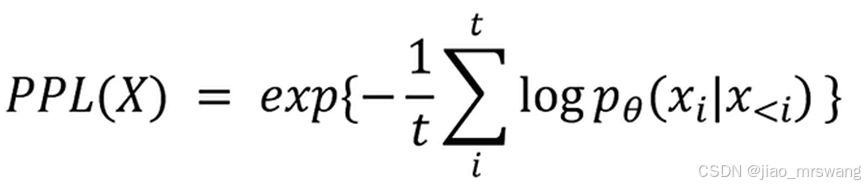
文本生成类(机器翻译)系统评估
在机器翻译任务中常用评价指标:BLEU、ROGUE、METEOR、PPL。 这些指标的缺点:只能反应模型输出是否类似于测试文本。 BLUE(Bilingual Evaluation Understudy):是用于评估模型生成的句子(candidate)和实际句子(referen…...
11.7【miniob】【debug】
这里的vector是实际值,而relation是指针,所以要解引用,*$1,并在最后调用其析构函数 emplace_back 和 push_back 都是用于在容器(如 std::vector)的末尾添加元素的方法,但它们的工作方式有所不同…...

OSHI 介绍与使用
OSHI 介绍 OSHI(Operating System and Hardware Information)是一个开源的Java库,用于从操作系统和硬件层面获取系统资源的详细信息。它提供了对操作系统、硬件、CPU、内存、磁盘、网络接口等多种信息的访问,且不依赖于平台特定的…...
Hadoop生态圈框架部署(八)- Hadoop高可用(HA)集群部署
文章目录 前言一、部署规划二、Hadoop HA集群部署(手动部署)1. 下载hadoop2. 上传安装包2. 解压hadoop安装包3. 配置hadoop配置文件3.1 虚拟机hadoop1修改hadoop配置文件3.1.1 修改 hadoop-env.sh 配置文件3.3.2 修改 core-site.xml 配置文件3.3.3 修改 …...
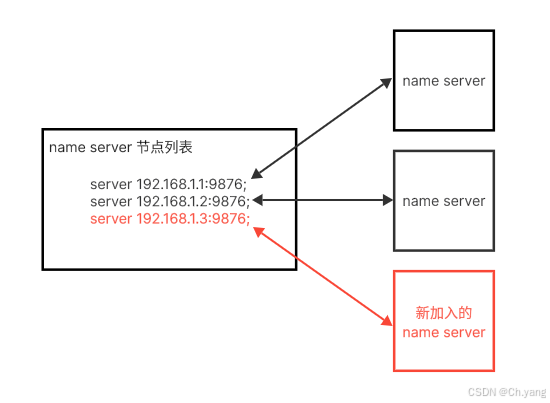
【RocketMQ】Name Server 无状态特点及如何让 Broker Consumer Producer 感知新节点
文章目录 前言1. Name Server 无状态特点2. Name Server 地址服务3. Name Server 手动配置后记 前言 看了 《RocketMQ 消息中间件实战派(上册)》前面一点,书中代码太多容易陷入细节。 这里简单描述下 RocketMQ Name Server 无状态表现在什么…...
蓝牙定位的MATLAB程序,四个锚点、三维空间
这段代码通过RSSI信号强度实现了在三维空间中的蓝牙定位,展示了如何使用锚点位置和测量的信号强度来估计未知点的位置。代码涉及信号衰减模型、距离计算和最小二乘法估计等基本概念,并通过三维可视化展示了真实位置与估计位置的关系。 目录 程序描述 运…...

机器学习--绪论
开启这一系列文章的初衷,是希望搭建一座通向机器学习世界的桥梁,为有志于探索这一领域的读者提供系统性指引和实践经验分享。随着人工智能和大数据技术的迅猛发展,机器学习已成为推动技术创新和社会变革的重要驱动力。从智能推荐系统到自然语…...
详解)
Unity 设计模式-命令模式(Command Pattern)详解
命令模式(Command Pattern)是一种行为型设计模式,它将请求封装成对象,从而使得可以使用不同的请求、队列或日志请求,以及支持可撤销的操作。命令模式通常包含四个主要角色:命令(Command…...

线程信号量 Linux环境 C语言实现
既可以解决多个同类共享资源的互斥问题,也可以解决简易的同步问题 头文件:#include <semaphore.h> 类型:sem_t 初始化:int sem_init(sem_t *sem, int pshared, unsigned int value); //程序中第一次对指定信号量调用p、v操…...
karmada-descheduler
descheduler规则 karmada-descheduler 定期检测所有部署,通常是每2分钟一次,并确定目标调度集群中无法调度的副本数量。它通过调用 karmada-scheduler-estimator 来完成这个过程。如果发现无法调度的副本,它将通过减少 spec.clusters 的配…...

【热门主题】000075 探索嵌入式硬件设计的奥秘
前言:哈喽,大家好,今天给大家分享一篇文章!并提供具体代码帮助大家深入理解,彻底掌握!创作不易,如果能帮助到大家或者给大家一些灵感和启发,欢迎收藏关注哦 💕 目录 【热…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...
