二维立柱图|积水类问题

三类问题
- 求总的积水量
- 求水坑的个数
- 求水坑最深的深度
基本思路
我们需要从列的角度来看第 i i i 列是不是有积水,但我们该如何确定第 i i i 列是否是有积水?
方法是事先维护一个前后缀的最大值, L [ i ] L[i] L[i] 和 R [ i ] R[i] R[i] 分别表示 [ 1 , i ] [1,i] [1,i] 和 [ i , n ] [i,n] [i,n] 中障碍物的最高高度,那么对于第 i i i 列,如果满足 L [ i ] > h [ i ] & & h [ i ] < R [ i ] L[i]> h[i] ~\&\&~ h[i]< R[i] L[i]>h[i] && h[i]<R[i],那么就证明它是低洼地,且水深就是 m i n ( L [ i ] , R [ i ] ) − h [ i ] min(L[i],R[i])-h[i] min(L[i],R[i])−h[i]。
准备工作
int h[N], L[N], R[N], n;
//分别记录第i列的障碍物高度以及前后缀最大值
void work() {cin >> n;for (int i = 1; i <= n; i++) cin >> h[i];for (int i = 1; i <= n; i++) L[i] = max(L[i - 1], h[i]);for (int i = n; i >= 1; i--) R[i] = max(R[i + 1], h[i]);
}
求总的积水量
int get_sum() {int sum = 0;for (int i = 1; i <= n; i++) {if (L[i] > h[i] && h[i] < R[i]) {sum += min(L[i], R[i]) - h[i];}}return sum;
}
求水坑的个数
注意:即使两个相邻的水坑有相同高度的水平面,只要之间有障碍物相隔,就算是两个水坑。
解决办法:引入一个标记状态的数组 s t [ N ] st[N] st[N],表示第 i i i 列是否是水坑的一条,如果 s t [ i ] = = t r u e & & s t [ i − 1 ] = = t r u e st[i]==true~\&\&~st[i-1]==true st[i]==true && st[i−1]==true,那么就说明了他们是属于同一水坑,否则第 i i i 列就属于一个新的水坑。
bool st[N];//表示第i列是否是水坑的一条
int get_cnt() {int cnt = 0;for (int i = 1; i <= n; i++) {if (L[i] > h[i] && h[i] < R[i]) {if (!st[i - 1]) cnt++;st[i] = true;}}return cnt;
}
求水坑的最深的深度
int get_mx() {int mx = 0;for (int i = 1; i <= n; i++) {if (L[i] > h[i] && h[i] < R[i]) {mx = max(mx, min(L[i], R[i]) - h[i]);}}return mx;
}
例题
- 积水量 http://bailian.openjudge.cn/practice/4074/
- 有多少坑
题目描述
大雨过后,一些高低不平的地方就会形成积水,俗称为“坑”。
这里我们将问题简化为只考虑一段路面的横截面。我们将这一段截面上的土地分割成单位宽度的窄条,测量出每个窄条的高度。
假设有无穷多的水量从天而降,请你计算一下,这段路面上会形成多少个水坑?坑的最大深度是多少毫米?
输入
输入第一行给出一个正整数 N ( ≤ 100000 ) N(\leq 100000) N(≤100000)。随后一行给出 N N N 个非负整数,为路面横截面总左到右的单位宽度窄条的高度,以毫米为单位,不超过 1000 1000 1000。
输出
输出分两行,第一行输出水坑的个数,第二行输出所有水坑中最大的深度,以毫米为单位。
注意:即使两个相邻的水坑有相同高度的水平面,只要之间有窄条相隔,就算是两个水坑。
样例输入
12
1 4 2 10 7 1 2 1 8 3 1 2
样例输出
3
7
代码实现
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int h[N], L[N], R[N], n;
//分别记录第i列的障碍物高度以及前后缀最大值
bool st[N];//表示第i列是否是水坑的一条
void work() {cin >> n;for (int i = 1; i <= n; i++) cin >> h[i];R[n + 1] = 0;for (int i = 1; i <= n; i++) L[i] = max(L[i - 1], h[i]);for (int i = n; i >= 1; i--) R[i] = max(R[i + 1], h[i]);
}
int get_cnt() {int cnt = 0;for (int i = 1; i <= n; i++) {if (L[i] > h[i] && h[i] < R[i]) {if (!st[i - 1]) cnt++;st[i] = true;}}return cnt;
}
int get_mx() {int mx = 0;for (int i = 1; i <= n; i++) {if (L[i] > h[i] && h[i] < R[i]) {mx = max(mx, min(L[i], R[i]) - h[i]);}}return mx;
}
int main() {work();cout << get_cnt() << "\n" << get_mx();return 0;
}
相关文章:

二维立柱图|积水类问题
三类问题 求总的积水量求水坑的个数求水坑最深的深度 基本思路 我们需要从列的角度来看第 i i i 列是不是有积水,但我们该如何确定第 i i i 列是否是有积水? 方法是事先维护一个前后缀的最大值, L [ i ] L[i] L[i] 和 R [ i ] R[i] R[…...

vue前端实现导出页面为word(两种方法)
将vue页面导出为word文档,不用写模板,直接导出即可。 第一种方法(简单版) 第一步:安装所需依赖 npm install html-docx-js -S npm install file-saver -S第二步:创建容器,页面使用方法(简单版࿱…...

22. Three.js案例-创建旋转的圆环面
22. Three.js案例-创建旋转的圆环面 实现效果 知识点 WebGLRenderer (WebGL渲染器) THREE.WebGLRenderer 是Three.js中最常用的渲染器,用于将场景渲染到WebGL画布上。 构造器 new THREE.WebGLRenderer(parameters) 参数类型描述parametersObject可选参数对象&…...

Elasticsearch:使用阿里 infererence API 及 semantic text 进行向量搜索
在之前的文章 “Elasticsearch 开放推理 API 新增阿里云 AI 搜索支持”,它详细描述了如何使用 Elastic inference API 来针对阿里的密集向量模型,稀疏向量模型, 重新排名及 completion 进行展示。在那篇文章里,它使用了很多的英文…...

Linux WEB服务器的部署及优化
1.用户常用关于web的信息 1.1.什么是www www是world wide web的缩写,及万维网,也就是全球信息广播的意思。 通常说的上网就是使用www来查询用户所需要的信息。 www可以结合文字、图形、影像以及声音等多媒体,超链接的方式将信息以Internet…...

人工智能大模型LLM开源资源汇总(持续更新)
说明 目前是大范围整理阶段,所以存在大量机翻说明,后续会逐渐补充和完善资料,减少机翻并增加说明。 Github上的汇总资源(大部分英文) awesome-production-machine-learning 此存储库包含一系列精选的优秀开源库&am…...

目标跟踪算法:SORT、卡尔曼滤波、匈牙利算法
目录 1 目标检测 2 卡尔曼滤波 3《从放弃到精通!卡尔曼滤波从理论到实践》视频简单学习笔记 3.1 入门 3.2 进阶 3.2.1 状态空间表达式 3.2.2 高斯分布 3.3 放弃 3.4 精通 4 匈牙利算法 5 《【运筹学】-指派问题(匈牙利算法)》视…...

Java版-图论-拓扑排序与有向无环图
拓扑排序 拓扑排序说明 对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边<u,v>∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列…...

GTC2024 回顾 | 优阅达携手 HubSpot 亮相上海,赋能企业数字营销与全球业务增长
从初创企业入门到成长型企业拓展,再到 AI 驱动智能化运营,HubSpot 为企业的每步成长提供了全方位支持。 2024 年 11 月下旬,备受瞩目的 GTC2024 全球流量大会(上海)成功举办。本次大会汇聚了全国内多家跨境出海领域企业…...

eclipse启动的时候,之前一切很正常,但突然报Reason: Failed to determine a suitable driver class的解决
1、之前项目都是启动正常的,然后运行以后发现启动不了了,还会报错: 2、这个Reason: Failed to determine a suitable driver class,说是没有合适的驱动class spring:datasource:url: jdbc:sqlserver://192.168.1.101:1433;databa…...

_tkinter.TclError: can‘t find package tkdnd Unable to load tkdnd library.解决办法
Traceback (most recent call last): File “tkinterdnd2\TkinterDnD.py”, line 55, in _require _tkinter.TclError: can’t find package tkdnd During handling of the above exception, another exception occurred: Traceback (most recent call last): File “1.导入总表…...
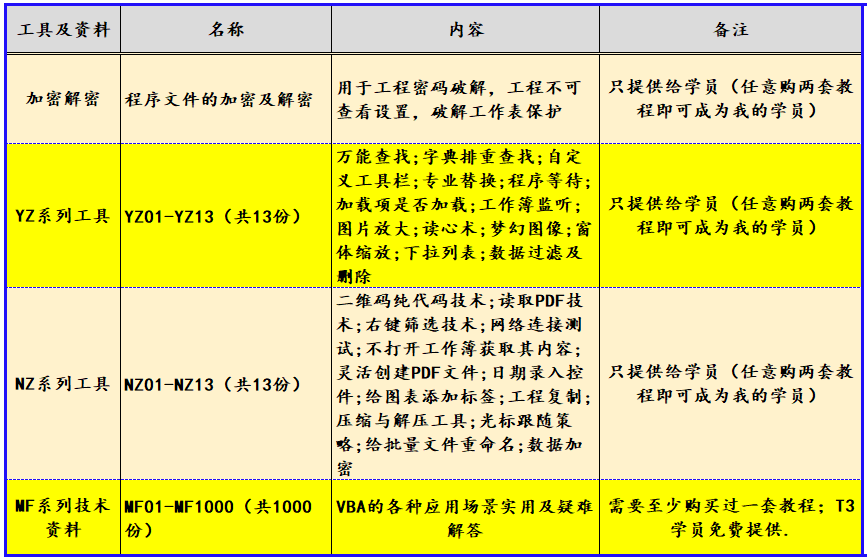
VBA高级应用30例应用在Excel中的ListObject对象:向表中添加注释
《VBA高级应用30例》(版权10178985),是我推出的第十套教程,教程是专门针对高级学员在学习VBA过程中提高路途上的案例展开,这套教程案例与理论结合,紧贴“实战”,并做“战术总结”,以…...

folly库Conv类型转换源码解析
1,普通类型转换 例子1: bool boolV = true;EXPECT_EQ(to<bool>(boolV), true);int intV = 42;EXPECT_EQ(to<int>(intV), 42);float floatV = 4.2f;EXPECT_EQ(to<float>(floatV), 4.2f);double doubleV = 0.42;EXPECT_EQ(to<double>(doubleV), 0.42)…...

UE4 骨骼网格体合并及规范
实现代码 // Fill out your copyright notice in the Description page of Project Settings.#pragma once#include "CoreMinimal.h" #include "SkeletalMeshMerge.h" #include "Kismet/BlueprintFunctionLibrary.h" #include "AceMeshCom…...

Java版企业电子招标采购系统源业码Spring Cloud + Spring Boot +二次开发+ MybatisPlus + Redis
功能描述 1、门户管理:所有用户可在门户页面查看所有的公告信息及相关的通知信息。主要板块包含:招标公告、非招标公告、系统通知、政策法规。 2、立项管理:企业用户可对需要采购的项目进行立项申请,并提交审批,查看所…...

通过源码⼀步⼀步分析 ArrayList 扩容机制
ArrayList 是 Java 中常用的集合类,它底层实现是基于数组的。为了处理元素的动态增加,ArrayList 会在容量不足时进行扩容。以下是通过源码逐步分析 ArrayList 扩容机制的过程。 1. ArrayList 类的基本结构 ArrayList 继承自 AbstractList,实…...

源码分析之Openlayers中默认Controls控件渲染原理
概述 Openlayers 中默认的三类控件是Zoom、Rotate和Attribution 源码分析 defaults方法 Openlayers 默认控件的集成封装在defaults方法中,该方法会返回一个Collection的实例,Collection是一个基于数组封装了一些方法,主要涉及到数组项的添…...

中间件的分类与实践:从消息到缓存
目录 一. 中间件的基本概念 二. 中间件的主要类型 (1)消息中间件(Message-Oriented Middleware, MOM): (2)数据库中间件: (3)Web中间件: &a…...

京东e卡 h5st 4.96
声明: 本文章中所有内容仅供学习交流使用,不用于其他任何目的,抓包内容、敏感网址、数据接口等均已做脱敏处理,严禁用于商业用途和非法用途,否则由此产生的一切后果均与作者无关! 有相关问题请第一时间头像私信联系我删…...
)
《CSS 知识点》滚动条仅在 hover 时才显示(宽度不改变)
很简单! 滚动条的滑动小方块背景色默认透明,仅在hover时设置背景色; 滚动条的轨道背景色默认透明,仅在hover时设置背景色; /*滚动条的滑动小方块*/ ::-webkit-scrollbar-thumb {background: transparent; } /*hover…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...
