【OpenCV】平滑图像
二维卷积(图像滤波)
与一维信号一样,图像也可以通过各种低通滤波器(LPF)、高通滤波器(HPF)等进行过滤。LPF 有助于消除噪音、模糊图像等。HPF 滤波器有助于在图像中找到边缘。
opencv 提供了函数 **cv.filter2D()**,用于将内核与图像卷积起来。作为一个例子,我们将尝试对图像进行均值滤波操作。5x5 均值滤波卷积核如下:

操作如下:将该内核中心与一个像素对齐,然后将该内核下面的所有 25 个像素相加,取其平均值,并用新的平均值替换这个25x25窗口的中心像素。它继续对图像中的所有像素执行此操作。试试下面这段代码并观察结果:
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
img = cv.imread('opencv_logo.png')
kernel = np.ones((5,5),np.float32)/25
dst = cv.filter2D(img,-1,kernel)
plt.subplot(121),plt.imshow(img),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(dst),plt.title('Averaging')
plt.xticks([]), plt.yticks([])
plt.show()图像模糊(图像平滑)
图像模糊是通过将图像与低通滤波核卷积来实现的。它有助于消除噪音。它实际上从图像中删除高频内容(例如:噪声、边缘)。所以在这个操作中边缘有点模糊。(好吧,有一些模糊技术不会使边缘太模糊)。OpenCV 主要提供四种模糊技术。
1、均值模糊
这是通过用一个归一化的滤波器内核与图像卷积来完成的。它只需取内核区域下所有像素的平均值并替换中心元素。这是通过函数 **cv.blur()**或 **cv.boxFilter()**完成的。有关内核的更多详细信息,请查看文档。我们应该指定滤波器内核的宽度和高度。3x3 标准化框滤波器如下所示:

注意 如果你不用标准化滤波,使用 **cv.boxFilter()**,传入 normalize=False 参数。
5x5 核的简单应用如下所示:
mport cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
img = cv.imread('opencv-logo-white.png')
blur = cv.blur(img,(5,5))
plt.subplot(121),plt.imshow(img),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(blur),plt.title('Blurred')
plt.xticks([]), plt.yticks([])
plt.show()
结果:

2、高斯模糊
在这种情况下,使用高斯核代替了核滤波器。它是通过函数 **cv.GaussianBlur()**完成的。我们应该指定内核的宽度和高度,它应该是正数并且是奇数(奇数才有一个中位数)。我们还应该分别指定 x 和 y 方向的标准偏差、sigmax 和 sigmay。如果只指定 sigmax,则 sigmay 与 sigmax 相同。如果这两个值都是 0,那么它们是根据内核大小计算出来的。高斯模糊是消除图像高斯噪声的有效方法。
如果需要,可以使用函数 **cv.getGaussianKernel()**创建高斯内核。
上述代码可以修改为高斯模糊:
blur = cv.GaussianBlur(img,(5,5),0)结果:

3、中值滤波
在这里,函数 **cv.medianBlur()**取内核区域下所有像素的中值,将中央元素替换为该中值。这对图像中的椒盐噪声非常有效。有趣的是,在上面的过滤器中,中心元素是一个新计算的值,它可能是图像中的像素值,也可能是一个新值。但在中值模糊中,中心元素总是被图像中的一些像素值所取代,可以有效降低噪音。它的内核大小应该是一个正的奇数整数。
在这个演示中,我在原始图像中添加了 50%的噪声,并应用了中间模糊。结果如下:
median = cv.medianBlur(img,5)结果:

4、双边滤波
**cv.bilateralFilter()**在保持边缘锐利的同时,对噪声去除非常有效。但与其他过滤器相比,操作速度较慢。我们已经看到高斯滤波器取像素周围的邻域并找到其高斯加权平均值。该高斯滤波器是一个空间函数,即在滤波时考虑相邻像素。但是它不考虑像素是否具有几乎相同的强度,也不考虑像素是否是边缘像素。所以它也会模糊边缘,这是我们不想做的。
双边滤波器在空间上也采用高斯滤波器,而另一个高斯滤波器则是像素差的函数。空间的高斯函数确保模糊只考虑邻近像素,而强度差的高斯函数确保模糊只考虑与中心像素强度相似的像素。所以它保留了边缘,因为边缘的像素会有很大的强度变化。
下面的示例显示使用双边滤波
blur = cv.bilateralFilter(img,9,75,75)结果:

apachecn.github.io/opencv-doc-zh/#/
相关文章:

【OpenCV】平滑图像
二维卷积(图像滤波) 与一维信号一样,图像也可以通过各种低通滤波器(LPF)、高通滤波器(HPF)等进行过滤。LPF 有助于消除噪音、模糊图像等。HPF 滤波器有助于在图像中找到边缘。 opencv 提供了函数 **cv.filter2D()**&…...
)
LeetCode300. 最长递增子序列(2024冬季每日一题 30)
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的 子序列。 示例 1&…...
vue H5如何实现copy功能
vue H5如何实现copy功能 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><link rel"stylesheet" href"https://unpkg.com/vant2.12/lib/index.css" /><title></title><st…...

Golang使用etcd构建分布式锁案例
在本教程中,我们将学习如何使用Go和etcd构建分布式锁系统。分布式锁系统对于管理对分布式系统中共享资源的并发访问至关重要。它有助于维护一致性,防止竞争条件,并确保在任何给定时间只有一个进程独占访问资源。 我们将使用Go作为编程语言&am…...
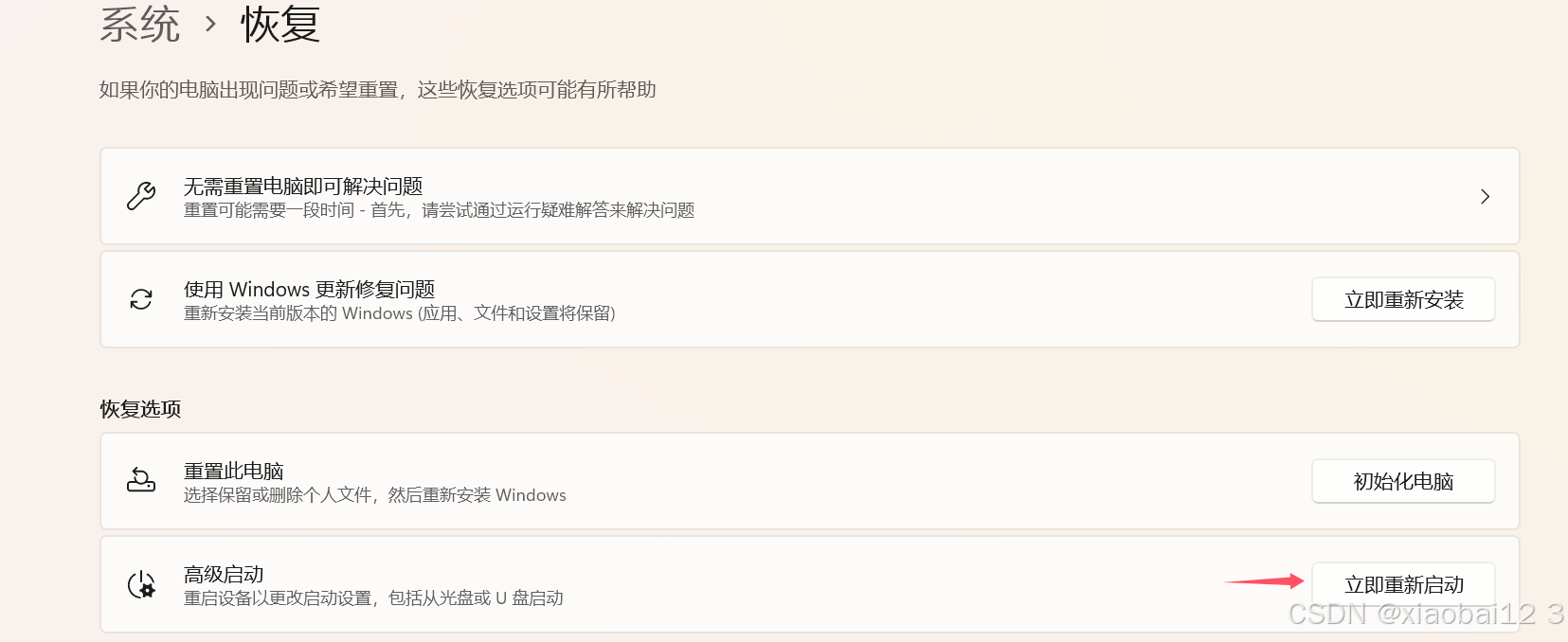
Windows 和 Ubuntu 双系统安装
复现论文的时候,个别包只有Linux版本,并且源码编译比较麻烦,所以干脆直接安装一个双系统(WinUbuntu),方便复现论文。 参考视频链接:Windows 和 Ubuntu 双系统的安装和卸载 0.所需工具 4G以上U…...
过程)
多媒体文件解复用(Demuxing)过程
多媒体文件的解复用(Demuxing)过程指的是从一个多媒体容器文件(如 MP4、MKV、AVI 等)中提取不同类型的多媒体数据流(例如视频流、音频流、字幕流等)的过程。 容器文件本身并不包含实际的视频或音频数据&…...
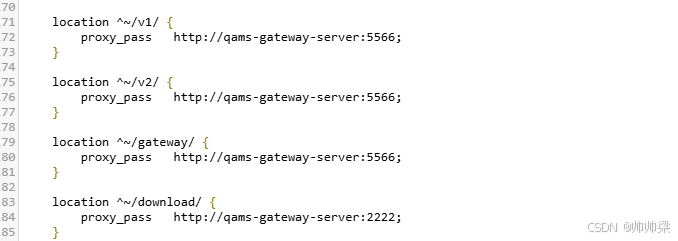
从 Zuul 迁移到 Spring Cloud Gateway:一步步实现服务网关的升级
从 Zuul 迁移到 Spring Cloud Gateway:一步步实现服务网关的升级 迁移前的准备工作迁移步骤详解第一步:查看源码第二步:启动类迁移第三步:引入 Gateway 依赖第四步 编写bootstrap.yaml第五步:替换路由配置第六步&#…...

qt之插件编译
QtXlsxWriter sudo apt install qtbase5-private-dev git clone https://github.com/dbzhang800/QtXlsxWriter.git cd QtXlsxWriter/ qmake make -j6 sudo make install #将生成的lib 及 include copy至项目路径的lib 及include里项目配置: QT xlsxbluetoo…...
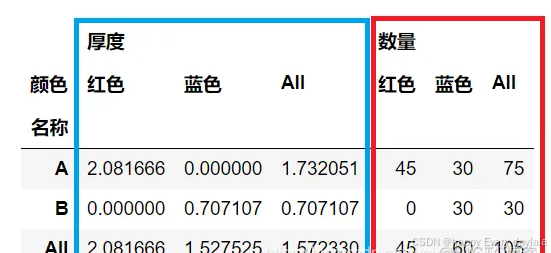
pandas一行拆成多行
import pandas as pd df pd.DataFrame({Country:[China,US,Japan,EU,UK/Australia, UK/Netherland],Number:[100, 150, 120, 90, 30, 2],Value: [1, 2, 3, 4, 5, 6],label: list(abcdef)})# 法一 推荐 df2df.drop(Country, axis1).join(df[Country].str.split(/, expandTrue).…...

今天调了个转速的小BUG
同事说转速表有个bug,转速停止后,继电器没有恢复到初始状态。若停止之前是报警,继电器吸合,则停止后继电器还是吸合。我心想不会啊,这软件都弄了好几年了,一直也没出现过状况。 经过与调试同事的沟通&#…...
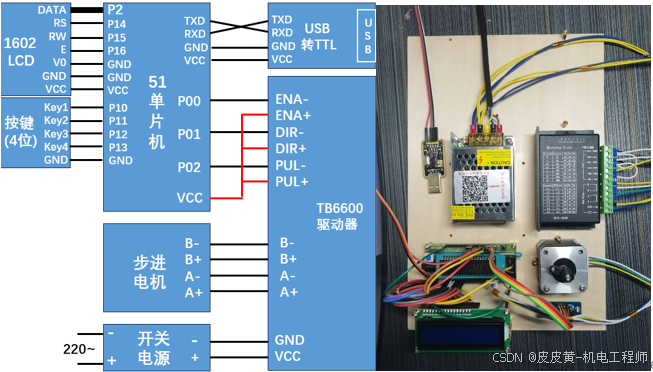
第三节、电机定速转动【51单片机-TB6600驱动器-步进电机教程】
摘要:本节介绍用定时器定时的方式,精准控制脉冲时间,从而控制步进电机速度 一、计算过程 1.1 电机每一步的角速度等于走这一步所花费的时间,走一步角度等于步距角,走一步的时间等于一个脉冲的时间 w s t e p t … ……...

从一个Bug谈前端响应拦截器的应用
一、问题场景 今天在开发商品管理系统时,遇到了一个有趣的问题:当添加重复的商品编号时,页面同时弹出了两条 "商品编号已存在" 错误提示: 这个问题暴露了前端错误处理机制的混乱,让我们从这个问题出发&…...

JS进阶DAY4|节点操作
嘿👋 今天我们要一起深入探索JavaScript中的DOM操作,这是前端开发中不可或缺的技能。🌟 准备好了吗?让我们一起跳进DOM的海洋,看看怎么用代码操控网页的结构吧! 目录 1. 增加节点 1.1 使用 appendChild 方…...
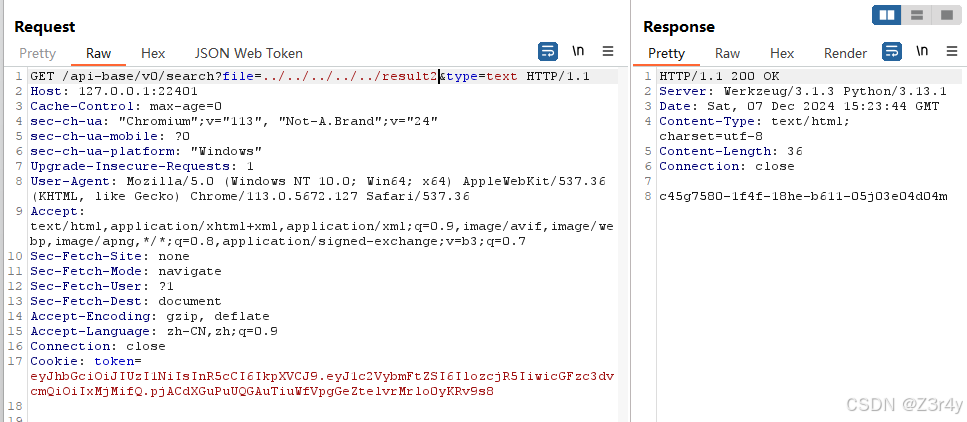
【Web】2023安洵杯第六届网络安全挑战赛 WP
目录 Whats my name easy_unserialize signal Swagger docs 赛题链接:GitHub - D0g3-Lab/i-SOON_CTF_2023: 2023 第六届安洵杯 题目环境/源码 Whats my name 第一段正则用于匹配以 include 结尾的字符串,并且在 include 之前,可以有任…...

go 语言中协程和GMP模型
为什么需要协程? 协程用来更加精细地利用线程,支撑超高的并发的。协程,从 runtime 的角度看,协程就是一个被调度的 g 结构体。 G 就是协程,M 是线程,P 是为了优化多线程并发时,会抢夺协程队列的…...

coco数据集转换SAM2格式
coco是一个大json汇总了所有train的标签 SAM2训练一张图对应一个json标签 import json import os from pycocotools import mask as mask_utils import numpy as np import cv2def poly2mask(points, width, height):points_array np.array(points, dtypenp.int32).reshape(-…...

【CMD、PowerShell和Bash设置代理】
【CMD、PowerShell和Bash设置代理】 1. CMD(命令提示符)临时设置代理(只对当前会话有效):查看当前代理设置:清除临时代理设置:永久设置代理(对所有新的 CMD 会话有效)&am…...

22智能 代码作业集合
3-2 #include <stdio.h>int main() {int a 21;int b 10;int c ;c a b;printf("Line 1 - c 的值是 %d\n", c );c a - b;printf("Line 2 - c 的值是 %d\n", c );c a * b;printf("Line 3 - c 的值是 %d\n", c );c a / b;printf("…...

实现一个简单的后台架子(侧边栏菜单渲染,折叠,黑白主题,组件主题色,全屏,路由快捷栏)
目录 侧边栏菜单渲染 侧边栏折叠 黑白主题 全屏切换 切换组件主题色 tab快捷栏 代码 侧边栏菜单渲染 结合ElementPlus组件库进行实现 新建的Vue3项目,引入了格式化样式normalize.css和ElementPlus,并进行了全局引入 并进行了全局引入 设置高度为100% 粘贴ElementPlus的…...

vue3-canvas实现在图片上框选标记(放大,缩小,移动,删除)
双图版本(模板对比) 业务描述:模板与图片对比,只操作模板框选的位置进行色差对比,传框选坐标位置给后端,返回对比结果显示 draw.js文件: 新增了 createUuid,和求取两个数组差集的方…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...

Django RBAC项目后端实战 - 03 DRF权限控制实现
项目背景 在上一篇文章中,我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统,为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...

手动给中文分词和 直接用神经网络RNN做有什么区别
手动分词和基于神经网络(如 RNN)的自动分词在原理、实现方式和效果上有显著差异,以下是核心对比: 1. 实现原理对比 对比维度手动分词(规则 / 词典驱动)神经网络 RNN 分词(数据驱动)…...

DL00871-基于深度学习YOLOv11的盲人障碍物目标检测含完整数据集
基于深度学习YOLOv11的盲人障碍物目标检测:开启盲人出行新纪元 在全球范围内,盲人及视觉障碍者的出行问题一直是社会关注的重点。尽管技术不断进步,许多城市的无障碍设施依然未能满足盲人出行的实际需求。尤其是在复杂的城市环境中ÿ…...
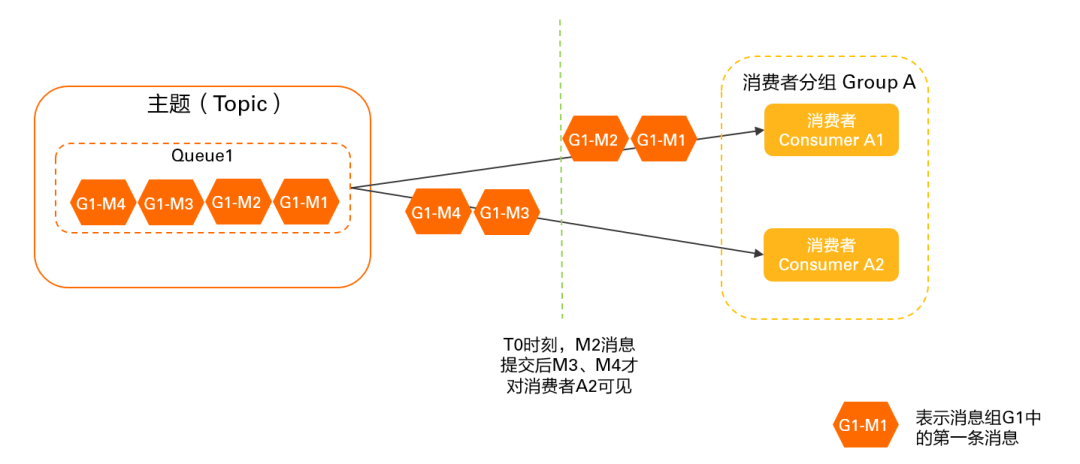
RocketMQ 客户端负载均衡机制详解及最佳实践
延伸阅读:🔍「RocketMQ 中文社区」 持续更新源码解析/最佳实践,提供 RocketMQ 专家 AI 答疑服务 前言 本文介绍 RocketMQ 负载均衡机制,主要涉及负载均衡发生的时机、客户端负载均衡对消费的影响(消息堆积/消费毛刺等…...
