数据结构与算法学习笔记----树与图的深度优先遍历
数据结构与算法学习笔记----树与图的深度优先遍历
@@ author: 明月清了个风
@@ first publish time: 2024.12.9
pa⭐️这里只有一道题哈哈。
Acwing 846.树的重心
给定一棵树,树中包含 n n n个节点(编号 1 ∼ n 1 \sim n 1∼n)和 n − 1 n - 1 n−1条无向边。
请你找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
输入格式
第一行包含整数 n n n,表示树的节点数。
接下来 n − 1 n - 1 n−1行,每行包含两个整数 a a a和 b b b,表示点 a a a和 b b b之间存在一条边。
输出格式
输出一个整数 m m m,表示将重心删除后,剩余各个连通块中点数的最大值。
数据范围
1 ≤ n ≤ 1 0 5 1 \leq n \leq 10^5 1≤n≤105
输入样例
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
输出样例
4
思路
首先是建树,使用的还是邻接表的方式,这个在哈希表中讲过了,如果不太懂可以去看一下,这题中的注意点就是因为是无向边,所以存的边数需要乘两倍
为什么用dfs:根据题意,我们需要在树中找到重心,而重心会将树划分为不同的连通块,我们需要统计的是不同连通块中点的数目,因此可以考虑dfs,这里大家可能会说为什么不是bfs,其实也可以,但是相对来说,bfs更强调点与点之间层级的概念,而这里我们只需要统计即可,因此dfs可能更加合适。
-
现在以输入样例中的树的形状为例解释一下题意(这里提前告诉大家重心是
1号点):我们从
1号点开始dfs(在这题里面其实从存在点开始就行,哪个点不重要,以后会碰到有些题对起始点也有考虑的)。根据题意我们将
1号点删除后,会将树分为 3 3 3个连通块,如图所示,那么对于1号点来说,剩余连通块中点数的最大值就是4(图中紫色背景的连通块);将
2号点删除后,会将树分为 2 2 2个连通块,那么对于2号点来说,剩余连通块中点数的最大值就是6(图中紫色背景的连通块);以此类推…(需要注意的是这并不是dfs的顺序,只是用来说明题意)

-
代码思路
既然已经考虑使用dfs进行解决,那么就要考虑dfs中具体需要维护的内容了。
-
首先最基本的就是连通块中点的统计,这很简单,伪代码如下
以上面的图(a)距离来说,我们
dfs(1)后,会在for循环中找到三个点2, 7, 4,这里就以2举例,那么对于2来说,我们会搜到他能到的点是1, 8, 5,但是我们是从1过来的,标记了st[1] = true,因此不会往回走了(这里是一个重点,后面会重新提到),所以dfs(2)中的for循环只会遍历到8, 5,那么对于这两个点也是同样的情况,不会往回走,但是他们的for中没有别的点可以走了,因此就是直接返回sum + 1 = 0 + 1 = 1。int dfs(int u) {st[u] = true; // 标记这个点搜过了int sum = 0; // 记录以这个点所在连通块的点的总数for(int i = h[u]; i != -1; i = ne[i]) // 连通块的遍历{int j = e[i]; // 取出u通向的点if(st[j]) continue; // 判断这个点搜过了没有int s = dfs(j); // 递归搜j点所在连通块的点的总数,因为这个连通块中搜过的点都会被标记,所以不会重复搜sum += s; // 加上递归搜到的总数,}return sum + 1; } -
然后是删除该点后连通块的最大值的维护
因为我们的dfs返回的是该点所在连通块中点的总数,但是我们需要维护的是删除该点后,剩下几个连通块中点数的最大值,也就是不包含这一点,因此这个量我们需要在
for循环中维护,因为for循环中,我们会遍历所有当前点能去到的点并统计其所在连通块的点数int s =dfs(j),这就相当于将u点删除后,他分割出的一个连通块的点的总数,因此只需要对这个量取最大值即可,增加一个量size进行维护size = max(size, s),代码修改如下:int dfs(int u) {st[u] = true; // 标记这个点搜过了int size = 0; // 记录删除当前点u后分割出的连通块的点数的最大值int sum = 0; // 记录以这个点所在连通块的点的总数for(int i = h[u]; i != -1; i = ne[i]) // 连通块的遍历{int j = e[i]; // 取出u通向的点if(st[j]) continue; // 判断这个点搜过了没有int s = dfs(j); // 递归搜j点所在连通块的点的总数,因为这个连通块中搜过的点都会被标记,所以不会重复搜size = max(size, s);sum += s; // 加上递归搜到的总数,}return sum + 1; } -
最后就是所有剩下连通块的点数的最大值的最小值
在上述dfs过程中,我们就可以维护出删除每个点后分割出的连通块的点数的最大值,要求最小值只需要用一个全局变量
ans进行维护就行,这里的一个注意点就是在上面第一点蓝字中提到的重点。还是以点2为例子,我们在第一层dfs(1)中已经将st[1] = true标记了,但是根据树的重心的定义,删除点2后,图(b)中紫色背景部分同样也是一个连通块,但是因为1被标记了所以在dfs(2)的for中不会向1走,那么1所在连通块的点数如何处理呢,这同样有可能改变最后size维护的大小,我们需要在for循环后加一步更新操作size = max(size, n - sum - 1);,已知当前点所在连通块的数量(包含当前点)是我们的返回值sum + 1,那么所有点减去这个量n - sum - 1,就是往回走的剩下那个连通块的点的数量,这里再和for循环中维护的size取个最大值就能保证没有遗漏了。
-
代码
#include <iostream>
#include <cstring>using namespace std;const int N = 100010;int n;
int h[N], e[N * 2], ne[N * 2], idx; // 无向边,因此要存两倍的量,节点数不用两倍
bool st[N]; // flag数组,标记每个点是否被dfs过
int ans = N; // 要求的值是最小值,因此答案初始化为最大值void add(int a, int b) // 单链表的加边操作
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}int dfs(int u) // dfs的返回值是dfs的这个点所在连通块的点的总数
{st[u] = true; // 标记这个点被搜过了 // size表示删除这个点的话,剩余每个连通块中包含点数最大值,因此初始化为0// sum表示当前dfs的点所在连通块的点的总数(不包含当前点),因此最后返回的是sum + 1int size = 0, sum = 0; for(int i = h[u]; i != -1; i = ne[i]) // 遍历这个点能去到的所有的点,dfs后就能找到他们所在连通块的点的最大值(存在size里了){int j = e[i];if(st[j]) continue; // 判断点有没有被搜过int s = dfs(j); // s存的就是这个点所在连通块包含的点的总数,size = max(size, s); // 找最大值sum += s; // 加在当前dfs的点的总数里,也就是点u所在连通块的总的点数中}// 这里是个细节,因为我们是随便找一个点开始遍历,比如这里我们搜的是1,但是我们并不知道重心是谁// 因此可能搜到后面的时候,往回走的点已经被搜过了,因此还要对比出去这个点的总数剩下的那个连通块的点的总数的大小,看图size = max(size, n - sum - 1); ans = min(ans, size);return sum + 1;
}int main()
{cin >> n;memset(h, -1, sizeof h);for(int i = 0; i < n - 1; i ++){int a, b;cin >> a >> b;add(a, b), add(b, a);}dfs(1);cout << ans << endl;return 0;
}
1; i ++){int a, b;cin >> a >> b;add(a, b), add(b, a);}dfs(1);cout << ans << endl;return 0;
}
相关文章:

数据结构与算法学习笔记----树与图的深度优先遍历
数据结构与算法学习笔记----树与图的深度优先遍历 author: 明月清了个风 first publish time: 2024.12.9 pa⭐️这里只有一道题哈哈。 Acwing 846.树的重心 给定一棵树,树中包含 n n n个节点(编号 1 ∼ n 1 \sim n 1∼n)和 n − 1 n - 1 n…...

IEEE T-RO 软体机器人手指状态估计实现两栖触觉传感
摘要:南方科技大学戴建生院士、林间院士、万芳老师、宋超阳老师团队近期在IEEE T-RO上发表了关于软体机器人手指在两栖环境中本体感知方法的论文。 近日,南方科技大学戴建生院士、林间院士、万芳老师、宋超阳老师团队在机器人顶刊IEEE T-RO上以《Propri…...
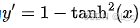
【NLP 14、激活函数 ② tanh激活函数】
学会钝感力,走向美好的方向 —— 24.12.11 一、tanh激活函数 1. tanh函数的定义 tanh是双曲正切函数(Hyperbolic Tangent),数学表达式为 其函数图像是一个S型曲线,以原点 (0,0) 为中心对称,定…...

前端如何实现签名功能
1.JS实现 前端实现签名功能,通常是通过在页面上创建一个可绘制的区域,用户可以用鼠标或触摸设备进行签名。这个区域通常是一个<canvas>元素,结合JavaScript来处理绘制和保存签名。下面是一个简单的实现步骤: 1.1. 创建HTM…...

若依将数据库更改为SQLite
文章目录 1. 添加依赖项2. 更新配置文件 application-druid.yml2.1. 配置数据源2.2. 配置连接验证 3. 更新 MybatisPlusConfig4. 解决 mapper 中使用 sysdate() 的问题4.1. 修改 BaseEntity4.2. 修改 Mapper 5. 更新 YML 配置 正文开始: 前提条件:在您的…...

CRMEB Pro版v3.2源码全开源+PC端+Uniapp前端+搭建教程
一.介绍 crmeb pro版 v3.2正式发布,全新UI重磅上线,焕然一新,不负期待!页面DIY设计功能全面升级,组件更丰富,样式设计更全面;移动端商家管理,让商城管理更便捷,还从页面…...
Docker 安装 Jenkins:2.346.3
准备:已安装Docker,已配置服务器安全组规则 1581 1、拉取镜像 [rootTseng ~]# docker pull jenkins/jenkins:2.346.3 2.346.3: Pulling from jenkins/jenkins 001c52e26ad5: Pull complete 6b8dd635df38: Pull complete 2ba4c74fd680: Pull complet…...
【OpenCV】模板匹配
理论 模板匹配是一种在较大图像中搜索和查找模板图像位置的方法。为此,OpenCV 带有一个函数 cv.matchTemplate() 。它只是在输入图像上滑动模板图像(如在 2D 卷积中),并比较模板图像下的模板和输入图像的补…...

黑马商城微服务复习(5)
MQ 一、同步调用和异步调用1. 同步调用2. 异步调用 二、RabbitMQ1. 基础使用2. 实际操作 怎么用?3. RabbitMQ虚拟主机 数据隔离4. 在JAVA中实现RabbitMQ5. 交换机种类 一、同步调用和异步调用 1. 同步调用 微服务一旦拆分,必然涉及到服务之间的相互调用ÿ…...
云原生基础设施指南:精通 Kubernetes 核心与高级用法
1. 云原生的诞生 随着互联网规模的不断增长,以及企业对敏捷开发、快速交付和高可用性的需求日益增强,传统的单体架构逐渐暴露出局限性,难以满足现代业务对动态扩展和高效迭代的要求。为此,云原生应运而生。 云原生是为云计算时代…...
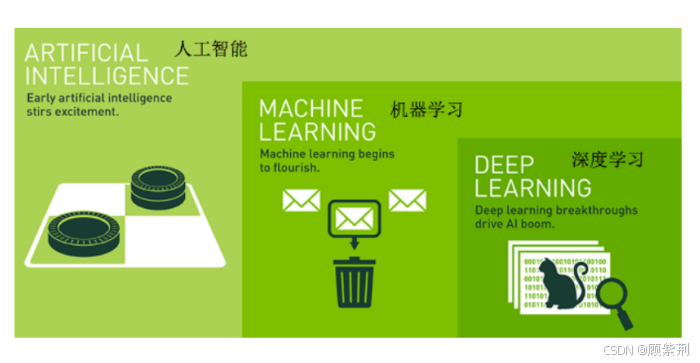
人工智能概要
目录 前言1.什么是人工智能(Artificial Intelligence, AI)2.人工智能发展的三次浪潮2.1 人工智能发展的第一次浪潮2.2 人工智能发展的第二次浪潮2.3 人工智能发展的第三次浪潮 3.人工智能发展的必备三要素3.1 数据3.2 算法(algorithm…...

qt QCommandLineParser详解
1、概述 QCommandLineParser是Qt框架中提供的一个类,专门用于解析命令行参数。它简化了命令行参数的处理过程,使得开发者能够轻松定义、解析和验证命令行选项和参数。QCommandLineParser适用于需要从命令行获取输入的控制台应用程序,以及需要…...

力扣 K个一组翻转链表
K个一组翻转链表 /*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(ne…...
cnocr配置及训练测试
cnocr配置及训练测试 1,相关链接2,已有模型调用测试(1)下载相关模型(2)Cnstd文本检测模型(3)模型调用解析脚本 3,自定义数据集训练测试(1)标签转换…...

解决 Flutter 在 Mac 上的编译错误
解决 Flutter 在 Mac 上的编译错误 在使用 Flutter 进行项目开发并尝试在 Mac 设备上进行编译时,遇到了一系列的错误信息,这些错误信息给项目的构建与部署带来了阻碍。 一、错误详情 在编译过程中,Xcode 输出了大量的信息,其中…...
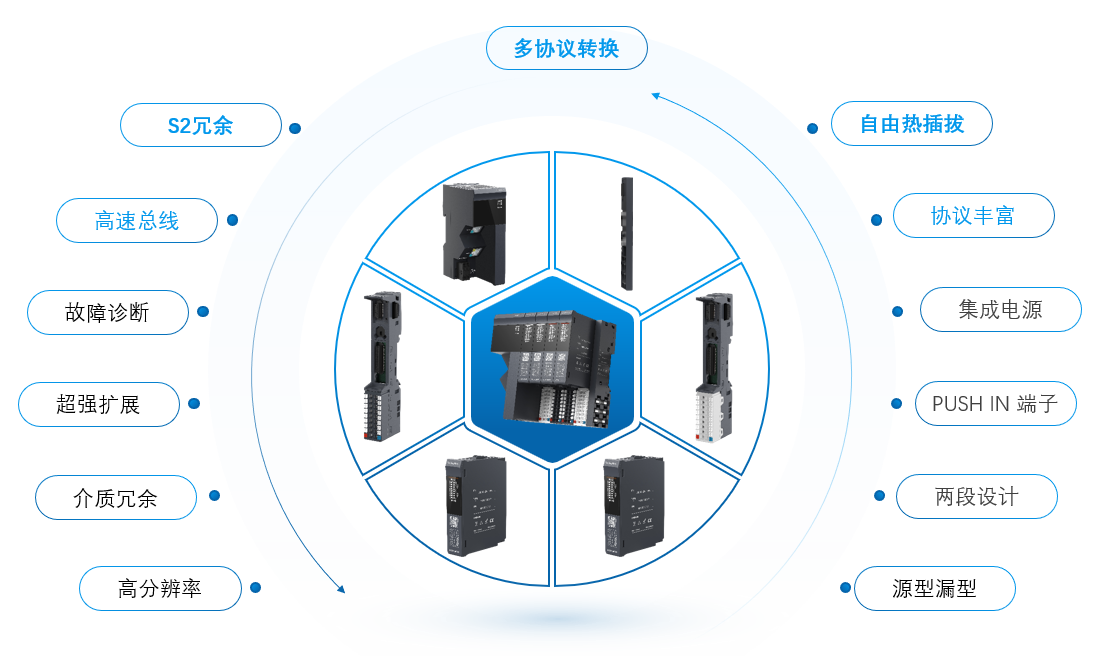
MR30分布式IO在新能源领域加氢站的应用
导读 氢能被誉为21世纪最具发展潜力的清洁能源,氢能科技创新和产业发展持续得到各国青睐。氢能低碳环保,燃烧的产物只有水,是用能终端实现绿色低碳转型的重要载体。氢能产业链分别为上游制氢、中游储运以及下游用氢。上游制氢工艺目前大部分…...
wxPython中wx.ListCtrl用法(二)
wx.ListCtrl是一个列表组件,可以以列表视图(list view)、报表视图(report view)、图标视图(icon view)和小图标视图(small icon view)等多种模式显示列表。 一、方法 __…...

kubernetes 资源汇总
kubernetes 资源汇总 官网 英文文档 官方英文文档 中文文档 官方中文文档 github github源码地址 培训认证 也就是linux基金会的认证,上面也提供培训课程 下载资源 官网下载资源,国内的话k8s镜像下载不了,要去镜像站 在线练习 killer…...
)
每日一题(对标gesp三级答案将在第二天公布)
编程题 题目描述: 小杨为数字4,5,6和7设计了一款表示形式,每个数字占用了66的网格。数字4,5,6和7的表示形式如下(此处自行设计复杂一些的表示形式示例): 数字4: …. …. …. …. *… 数字5: …...

让 Win10 上网本 Debug 模式 QUDPSocket 信号槽 收发不丢包的方法总结
在前两篇文章里,我们探讨了不少UDP丢包的解决方案。经过几年的摸索测试,其实方法非常简单, 无需修改代码。 1. Windows 下设置UDP缓存 这个方法可以一劳永逸解决UDP的收发丢包问题,只要添加注册表项目并重启即可。即使用Qt的信号与槽&#…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...
