算法知识-15-深搜
一、概念
深度优先搜索(Deep First Search, DFS)是一种用于遍历或搜索树或图的算法。这种策略沿着树的深度遍历树的节点,尽可能深地搜索树的分支。
二、关键步骤
选择起点:根据题目要求,选择一个或多个节点作为搜索的起点。
递归搜索:从起点开始,递归地访问每个节点的所有未访问的邻接节点。
回溯:当到达一个节点,且这个节点没有未访问的邻接节点时,递归过程将回溯,尝试其他可能的路径。
记录状态:在递归前后,正确地记录和恢复状态(如访问状态、路径记录等)是非常重要的。
三、代码模板
以下题为例,说明关于深搜的几个模板
①看能不能到达
②能到达几次
③连通块,几个区域
1744 迷宫
有 1 个 n×n 的迷宫方格,在方格内“0”表示可以通行,“1”表示是障碍物不能通行,在(n,n)位置有一个宝箱。现在有个人在左上角( 1 , 1 )的位置,他在迷宫内可以向当前位置的上、下、左、右四个方向行走,能不能在迷宫里走到宝箱位置( n,n )。注意:测试数据保证起点和终点均为“0”,走的过程不能走出迷宫。
输入描述
输入第一行为 n(2 ≤n≤10 ),表示 n×n 的方格,接下来有 n 行,每行 n 个整数, 0 表示可以行走,1 表示不能行走,每个整数之间有个空格。
输出描述
如果可以走到终点,输出“YES”,否则输出“NO”
样例输入 1
3
0 0 1
1 0 0
0 1 0
样例输出 1
YES
题目分析:
首先我们输入,n,n行n列的数据【根据不同题目可能输入的数据存到字符串数组】
然后标记开始的位置【比如此题中开始位置就是 1,1,即一行一列的位置】,同时明确终点位置就是n,n【即n行n列】
然后开始搜索,构建搜索函数dfs,这个函数中,我们会走四个方向,所以使用两个一维数组表示四个方向坐标的改变的值
或者大家可以使用二维数组,我们还要构建一个标记数组,以下代码使用的是book数组来标记
函数中我们首先判断当前坐标是不是终点,如果是终点,就停止搜索【根据题目分析,有些题目不能终止,而是去计数】
然后再判断四个方向【不同题目,方向的数目不同】,计算新的落脚点
判断新的落脚点【nx,ny】是不是符合要求,此题中,需要满足三个条件①不越界;②没标记;③是可以通行的;
如果可以通行,则标记这个新的落脚点,继续下一步的搜索
#include<bits/stdc++.h>
using namespace std;
int n,a[15][15],dx[4]={-1,1,0,0},dy[4]={0,0,-1,1},book[15][15]; //左右上下
bool flag;
void dfs(int x,int y){if(x == n && y == n){flag = true;return ;}for(int i=0;i<4;i++){int nx = x+dx[i],ny=y+dy[i];//出界 标记 if(nx>0&&nx<=n && ny>0&&ny<=n && book[nx][ny]==0 &&a[nx][ny]==0){book[nx][ny]=1;dfs(nx,ny);}}
}
int main(){cin >> n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin >> a[i][j];}}book[1][1]=1;dfs(1,1);if(flag) cout<<"YES";else cout << "NO";return 0;
}同样的,我们可以完成下面题目
2936 八个方向
已知山洞里面是由许多房间组成的迷宫,每个房间可以通往周围八个房间,迷宫大小是一个N*N的正方形,其中有一些蝙蝠堵路。现在从起始(1,1)的位置进入洞穴寻找宝藏(已有一个宝箱),如果可以找到宝藏输出YES,否则输出NO。
输入描述
第一行是一个正整数N(2<N ≤10),后面包含N*N行由0,1,2组成的矩阵,其中0表示可以走,1表示蝙蝠,2表示宝藏的位置。
(注意:第一个房间没有蝙蝠)
输出描述
一行,找到宝藏输出YES,否则输出NO 。
样例输入 1
6
0 0 1 1 0 0
1 0 0 1 0 0
0 0 0 1 2 0
0 1 1 1 0 0
0 0 0 1 0 0
0 0 0 1 0 0
样例输出 1
NO
样例输入 2
5
0 0 0 0 0
0 0 1 1 1
0 0 0 1 0
0 1 0 1 2
0 0 0 0 1
样例输出 2
YES
和迷宫的区别就是方向变多了
#include <bits/stdc++.h>
using namespace std;
int n,ex,ey,a[25][25],vis[105][105];
bool flag;
bool check(int nx,int ny){return nx>0&&nx<=n&&ny>0&&ny<=n&&vis[nx][ny]==0&&a[nx][ny]!=1;
}
int dx[8]={0,1,1,1,0,-1,-1,-1};//右,右下,下,左下,左,上,右上
int dy[8]={1,1,0,-1,-1,-1,0,1};//右,右下,下,左下,左,上,右上
void dfs(int x,int y){if(x==ex&&y==ey){//cout << x <<' '<< y;flag=1;return;}for(int i=0;i<8;i++){int nx=x+dx[i],ny=y+dy[i];if(check(nx,ny)){vis[nx][ny]=1;dfs(nx,ny);}}
}int main(){cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>a[i][j];if(a[i][j]==2) {ex=i;ey=j;}}}vis[1][1]=1;dfs(1,1);if(flag) cout<<"YES";else cout<<"NO";return 0;
}
3089 探索迷宫
水题,就不放题目了,自己找吧
#include <iostream>
using namespace std;
int n,m,x1,y1;
bool flag;
int vis[25][25];
int dx[4] = {1,0,-1,0},dy[4] = {0,1,0,-1};
int mp[25][25];
void dfs(int x,int y)
{if(x==x1 && y==y1){flag = 1;return ;}for(int i=0;i<4;i++){int nx = x+dx[i];int ny = y+dy[i];if(nx>0&&nx<=n&&ny>0&&ny<=m&&mp[nx][ny]!=1&&vis[nx][ny]==0){vis[nx][ny] = 1;dfs(nx,ny);}}}
int main() {cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>mp[i][j];}}if(mp[1][1]==1){cout<<"NO";return 0;}cin>>x1>>y1;vis[1][1] = 1;dfs(1,1);if(flag) cout<<"YES";else cout<<"NO";return 0;
}
3090 走迷宫
衍生版本,就是开始与结束位置也是自己输入的
#include<bits/stdc++.h>
using namespace std;
bool vis[105][105],f=0;
int n,x,y,startx,starty;
char c[105][105];
int dx[4] = {1,0,-1,0},dy[4] = {0,1,0,-1};
void dfs(int x1,int y1)
{if(x1==x && y1==y){f = 1;}for(int i=0;i<4;i++){int nx = x1+dx[i];int ny = y1+dy[i];if(nx>=0 && nx<n && ny>=0 && ny<n && vis[nx][ny]==0 && c[nx][ny]=='.'){vis[nx][ny] = 1;dfs(nx,ny);}}
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n;for(int i=0;i<n;i++){for(int j=0;j<n;j++){cin>>c[i][j];}}cin>>startx>>starty>>x>>y;if(c[startx][starty]=='#' or c[x][y]=='#'){cout<<"no";return 0;}else{dfs(startx,starty);}if(f==1) cout<<"yes";else cout<<"no";return 0;
}2936 八个方向
水题++,只有方向变多了,大家注意这个方向的数组一定要正确【此题copy杨同学的代码】
#include <bits/stdc++.h>
using namespace std;
int n,ex,ey,a[25][25],vis[105][105];
bool flag;
bool check(int x,int y){return x>=1&&x<=n&&y>=1&&y<=n&&!vis[x][y]&&a[x][y]!=1;
}
int dx[8]={-1,0,1,1,1,0,-1,-1},dy[8]={1,1,1,0,-1,-1,-1,0};
void dfs(int x,int y){if(x==ex&&y==ey){flag=1;return;}for(int i=0;i<8;i++){int nx=x+dx[i],ny=y+dy[i];if(check(nx,ny)){vis[nx][ny]=1;dfs(nx,ny);}}
}int main(){cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>a[i][j];if(a[i][j]==2){ex=i;ey=j;}}}if(a[1][1]==1){cout<<"NO";return 0;}vis[1][1]=1;dfs(1,1);if(flag) cout<<"YES";else cout<<"NO";return 0;
}
4143 中国象棋的马
做完八个方向,来看看这个,八个方向的衍生版本

不懂就看上图,再不懂?就微信私聊吧,啥也别说了
#include <bits/stdc++.h>
using namespace std;
int n,m,ex,ey,a[25][25],vis[105][105];
bool flag;
bool check(int x,int y){return x>=1&&x<=n&&y>=1&&y<=m&&!vis[x][y]&&a[x][y]!=1;
}
int dx[8]={-1,-2,-2,-1,1,2,2,1},dy[8]={2,1,-1,-2,-2,-1,1,2};
void dfs(int x,int y){if(x==ex&&y==ey){flag=1;return;}for(int i=0;i<8;i++){int nx=x+dx[i],ny=y+dy[i];if(check(nx,ny)){vis[nx][ny]=1;dfs(nx,ny);}}
}int main(){cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];}}cin>>ex>>ey;if(a[1][1]==1){cout<<"NO";return 0;}vis[1][1]=1;dfs(1,1);if(flag) cout<<"YES";else cout<<"NO";return 0;
}
说完这一类的题目,我们接下来看看统计线路相关的题目
2937 八个方向统计线路
已知山洞里面是由许多房间组成的迷宫,每个房间可以通往周围八个房间,迷宫大小是一个N*N的正方形,其中有一些蝙蝠堵路。现在从起始(1,1)的位置进入洞穴寻找宝藏(只有一个宝箱),统计有多少条线路可以找到宝藏。
输入描述
第一行是一个正整数N(2<N<6),后面包含N*N行由0,1,2组成的矩阵,其中0表示可以走,1表示蝙蝠,2表示宝藏的位置。
输出描述
一行,一个整数,表示可以找到宝藏的线路。
样例输入 1
6
0 0 1 1 0 0
1 0 0 1 0 0
0 0 0 1 2 0
0 1 1 1 0 0
0 0 0 1 0 0
0 0 0 1 0 0
样例输出 1
0
样例输入 2
2
0 0
0 2
样例输出 2
5
思路分析:这个题目,不是找一次终点,而是多次找终点,所以被归为一类的题目
这个题目的核心代码是
vis[nx][ny]=1;dfs(nx,ny);vis[nx][ny]=0;
就是我们标记当前位置搜索完毕后要把当前位置给去除标记再次搜索,看看有没有别的可能到达终点
代码如下【来自杨同学,后续不说明了哈】
// 来自杨同学,我就不写了,后面大抵都是他的代码,他把判断内容用check函数封装了
#include <bits/stdc++.h>
using namespace std;
int n,ex,ey,a[105][105],vis[105][105],sum;
bool check(int x,int y){return x>=1&&x<=n&&y>=1&&y<=n&&!vis[x][y]&&a[x][y]!=1;
}
int dx[8]={-1,0,1,1,1,0,-1,-1},dy[8]={1,1,1,0,-1,-1,-1,0};
void dfs(int x,int y){if(x==ex&&y==ey){sum++;return;}for(int i=0;i<8;i++){int nx=x+dx[i],ny=y+dy[i];if(check(nx,ny)){vis[nx][ny]=1;dfs(nx,ny);vis[nx][ny]=0;}}
}
int main(){cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>a[i][j];if(a[i][j]==2){ex=i;ey=j;}}}if(a[1][1]==1){cout<<0;return 0;}vis[1][1]=1;dfs(1,1);cout<<sum;return 0;
}
2935 统计线路
水++
//这个风格是邢同学的
#include<bits/stdc++.h>
using namespace std;
int vis[11][11],ans,n;
int mp[11][11];
int dx[4] = {1,0,-1,0};
int dy[4] = {0,1,0,-1};
void dfs(int x,int y)
{if(mp[x][y]==2){ans++;return ;} for(int i=0;i<4;i++){int nx = x+dx[i];int ny = y+dy[i];if(nx>0&&nx<=n&ny>0&&ny<=n&&vis[nx][ny]==0&&mp[nx][ny]!=1){vis[nx][ny] = 1;dfs(nx,ny);vis[nx][ny] = 0;}}
}
int main()
{cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>mp[i][j];}}vis[1][1] = 1;dfs(1,1);cout<<ans;return 0;
}1353 围成面积 **
这个题就好玩了
编程计算由数字1围成的下列图形的面积。面积计算方法是统计数字1所围成的闭合曲线中点的数目。如下图所示,在10 * 10的二维数组中,有数字1围住了15个点,因此面积为15。
0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 1 1 0 0 0
0 0 0 0 1 0 0 1 0 0
0 0 0 0 0 1 0 0 1 0
0 0 1 0 0 0 1 0 1 0
0 1 0 1 0 1 0 0 1 0
0 1 0 0 1 1 0 1 1 0
0 0 1 0 0 0 0 1 0 0
0 0 0 1 1 1 1 1 0 0
0 0 0 0 0 0 0 0 0 0
输入描述
输入一个包含 0 和 1 数字的 10∗10 矩阵
输出描述
输出面积
样例输入 1
0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 1 1 0 0 0
0 0 0 0 1 0 0 1 0 0
0 0 0 0 0 1 0 0 1 0
0 0 1 0 0 0 1 0 1 0
0 1 0 1 0 1 0 0 1 0
0 1 0 0 1 1 0 1 1 0
0 0 1 0 0 0 0 1 0 0
0 0 0 1 1 1 1 1 0 0
0 0 0 0 0 0 0 0 0 0
样例输出 1
15
分析一下:这个题要看1围起来的0的个数,我们要把这个题的数据分三部分,外层0,中层1,内层0,一共是10行10列,除去外层能搜索到的0的个数,输入时判断累加的1的个数,不就是中间的0的个数
上图

不理解的直接来找我
#include <bits/stdc++.h>
using namespace std;
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
int a[105][105],sum1,sum2,ans;
bool flag;
bool check(int x,int y){return x>=1&&x<=10&&y>=1&&y<=10&&a[x][y]!=1;
}
void dfs(int x,int y){a[x][y]=1;for(int i=0;i<=3;i++){int nx=x+dx[i],ny=y+dy[i];if(check(nx,ny)){sum2++;dfs(nx,ny);}}
}
int main(){for(int i=1;i<=10;i++){for(int j=1;j<=10;j++){cin>>a[i][j];if(a[i][j]==1) sum1++;}}for(int i=1;i<=10;i++){for(int j=1;j<=10;j++){if(a[i][j]==0){sum2++;dfs(i,j);flag=1;break;}}if(flag) break;}ans=100-sum1-sum2;cout<<ans;return 0;
}
6604 地图找车
水++
#include <bits/stdc++.h>
using namespace std;
char a[105][105];
int n,m,ex,ey,vis[105][105];
bool flag;
bool check(int x,int y){return x>=1&&x<=n&&y>=1&&y<=m&&!vis[x][y]&&a[x][y]!='X';
}
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
void dfs(int x,int y){if(x==ex&&y==ey){flag=1;return;}for(int i=0;i<4;i++){int nx=x+dx[i],ny=y+dy[i];if(check(nx,ny)){vis[nx][ny]=1;dfs(nx,ny);}}
}int main(){cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];if(a[i][j]=='*'){ex=i;ey=j;}}}if(a[1][1]=='X'){cout<<"NO";return 0;}vis[1][1]=1;dfs(1,1);if(flag) cout<<"YES";else cout<<"NO";return 0;
}
2929 寻宝
侠盗 Hank 经过千难万险终于来到了恶人岛,为了拿到恶人岛的宝座去帮助穷人,Hank 先对恶人岛进行了侦查,发现恶人岛有一个迷阵,宝藏摆在了迷阵的深处。迷阵由 M×N 个方 格组成,有的方格内有可以发现 Hank 的守卫,而有的方格内则是安全。为了展现自己的实 力,Hank 决定不仅要拿走恶人岛的宝藏,还要给他们留一封信,告诉恶人自己有 g 种方法 找到宝藏。现在要求你来帮助他实现这个目标。
迷阵越大,守卫越多。
输入描述
输入有一组测试数据,以两个非零整数 N 和 M 开始,两者均不大于20。N表示迷阵行数, M表示迷阵列数。接下来有 N 行, 每行包含 M 个字符,不同字符分别代表不同含义:
‘@’:Hank 所在的位置;
‘.’:可以安全通行的方格;
‘#’:有守卫的方格;
‘*’:宝藏所在位置。
输出描述
一个整数 g,表示 Hank 有 g 种方法可以找到宝藏。如果他不可能找到宝藏, 则输出-1。
样例输入 1
8 8
.@##…#
#…#.#
#.#.##…
…#.###.
#.#…#.
…###.#.
…#.*…
.#…###
样例输出 1
4
样例输入 2
9 6
.#…#.
.#.*.#
.####.
…#…
…#…
…#…
…#…
#.@.##
.#…#.
样例输出 2
-1
思路:水题,就是多个判断
#include <bits/stdc++.h>
using namespace std;
char a[105][105];
int n,m,fx,fy,ex,ey,vis[105][105],sum;
bool flag;
bool check(int x,int y){return x>=1&&x<=n&&y>=1&&y<=m&&!vis[x][y]&&a[x][y]!='#';
}
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
void dfs(int x,int y){if(x==ex&&y==ey){flag=1;sum++;return;}for(int i=0;i<4;i++){int nx=x+dx[i],ny=y+dy[i];if(check(nx,ny)){vis[nx][ny]=1;dfs(nx,ny);vis[nx][ny]=0;}}
}
int main(){cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];if(a[i][j]=='@'){fx=i;fy=j;}if(a[i][j]=='*'){ex=i;ey=j;}}}vis[fx][fy]=1;dfs(fx,fy);if(!flag) cout<<-1;else cout<<sum;return 0;
}
1791 多少块水洼
有一块 N×M 的土地,雨后积起了水,有水标记为‘W’,干燥为‘.’。八连通的积水被认为是连接在一起的。请求出院子里共有多少水洼?
输入描述
第一行为 N,M (1≤N,M≤100)。
下面为 N×M的土地示意图。
输出描述
一行,共有的水洼数。
样例输入 1
10 12
W…WW.
.WWW…WWW
…WW…WW.
…WW.
…W…
…W…W…
.W.W…WW.
W.W.W…W.
.W.W…W.
…W…W.
样例输出 1
3
思路:从每个点搜索,并且标记,如果搜索停止,就看下个点搜索的情况。看最后能搜索到几个区域,记得计数
#include<bits/stdc++.h>
using namespace std;
int vis[105][105];
char mp[105][105];
int n,m,ans;
int dx[8] = {0,1,1,1,0,-1,-1,-1};
int dy[8] = {1,1,0,-1,-1,-1,0,1};
void dfs(int x,int y)
{for(int i=0;i<8;i++){int nx = x+dx[i];int ny = y+dy[i];if(nx>=0 && nx<n && ny>=0 && ny<m && mp[nx][ny]=='W' && vis[nx][ny]==0){vis[nx][ny] = 1;dfs(nx,ny);}}
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>n>>m;for(int i=0;i<n;i++){for(int j=0;j<m;j++){cin>>mp[i][j];}}for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(mp[i][j]=='W'&& vis[i][j]==0){ans++;vis[i][j] = 1;dfs(i,j);}}}cout<<ans;return 0;
}1852 连通块
一个 n×m 的方格图,一些格子被涂成了黑色,在方格图中被标为 1,白色格子标为 0。问有多少个四连通的黑色格子连通块。四连通的黑色格子连通块指的是一片由黑色格子组成的区域,其中的每个黑色格子能通过四连通的走法(上下左右),只走黑色格子,到达该连通块中的其它黑色格子。
输入描述
第一行两个整数 n,m,表示一个 n×m 的方格图。
接下来 n 行,每行 m 个整数,分别为 0 或 1,表示这个格子是黑色还是白色。
输出描述
一行一个整数 ans,表示图中有 ans 个黑色格子连通块。
样例输入 1
3 3
1 1 1
0 1 0
1 0 1
样例输出 1
3
提示
数据范围与提示
1≤n,m≤100
#include <bits/stdc++.h>
using namespace std;
int dx[4]={-1,1,0,0},dy[4]={0,0,-1,1};
int n,m,a[105][105],sum;
bool check(int x,int y){return x>=1&&x<=n&&y>=1&&y<=m&&a[x][y]!=0;
}
void dfs(int x,int y){a[x][y]=0;for(int i=0;i<=3;i++){int nx=x+dx[i],ny=y+dy[i];if(check(nx,ny)){dfs(nx,ny);}}
}
int main(){cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(a[i][j]!=0){sum++;dfs(i,j);}}}cout<<sum;return 0;
}
6611 吃蛋糕
小童今天跟家人一起吃生日蛋糕庆祝生日,这块蛋糕是由n×m 的网格构成,每个网格上面都放有不同的水果。小童把这些水果分为两类,一类是自己喜欢吃的水果,用’#‘来表示;一类是自己不喜欢吃的水果,用’.'来表示。小童能吃到几块只包含自己喜欢吃的水果?一块蛋糕为上下左右为#的连通区域。
输入描述
第一行为两整数 n,m ,表示矩阵的大小为n×m(0<m,n≤100)。
从第二行开始是一个 n×m 的矩阵。
输出描述
一行,表示蛋糕块数
样例输入 1
4 5
.#.#.
.#.##
.##…
#…
样例输出 1
3
#include<bits/stdc++.h>
using namespace std;
int n,m;
int dx[4] = {1,-1,0,0};
int dy[4] = {0,0,1,-1};
int ans;
bool vis[105][105];
char g[105][105];
void dfs(int x,int y){for(int i=0;i<4;i++){int nx = x+dx[i];int ny = y+dy[i];if(nx>0 && nx<=n && ny>0 && ny<=m && g[nx][ny]=='#' && vis[nx][ny]==0){vis[nx][ny] = 1;dfs(nx,ny);}}
}
int main(){cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>g[i][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(g[i][j]=='#'&& vis[i][j]==0){ans++;vis[i][j] = 1;dfs(i,j);}}}cout<<ans;return 0;
}
6624 数地图连通块面积
#include<bits/stdc++.h>
using namespace std;
int n,m;
bool f;
int dx[4] = {1,0,-1,0};
int dy[4] = {0,1,0,-1};
int ans;
bool vis[105][105];
char g[105][105];
void dfs(int x,int y){for(int i=0;i<4;i++){int nx = x+dx[i];int ny = y+dy[i];if(nx>0 && nx<=n && ny>0 && ny<=m && g[nx][ny]=='#' && vis[nx][ny]==0){vis[nx][ny] = 1;ans++;dfs(nx,ny);}}
}
int main(){cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>g[i][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(g[i][j]=='#'&& vis[i][j]==0){vis[i][j] = 1;dfs(i,j);cout<<ans+1<<" ";ans = 0;f = 1;}}}if(f==0){cout<<-1;}return 0;
}
6822 红与黑
第一行是两个整数 n 和 m,表示房间是 n 行 m 列大小。在接下来的 n 行中,每行包括 m 个字符。每个字符表示一块瓷砖的颜色,规则如下:
‘.’:黑色的瓷砖;
‘#’:红色的瓷砖;
‘@’:黑色的瓷砖,并且你站在这块瓷砖上。该字符在数据中出现一次。
输出描述
一行,显示你从初始位置出发能到达的瓷砖数(注意:记数时包括初始位置的瓷砖)。
样例输入 1
5 6
…#.
…#
…
#@…#
.#…#.
样例输出 1
21
提示
数据范围与提示
1<n,m<20
注意此题中初始位置就是一个黑色区域,要计数
#include <bits/stdc++.h>
using namespace std;
char a[105][105];
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
int n,m,sum;
bool check(int x,int y){return x>=1&&x<=n&&y>=1&&y<=m&&a[x][y]!='#';
}
void dfs(int x,int y){a[x][y]='#';for(int i=0;i<=3;i++){int nx=x+dx[i],ny=y+dy[i];if(check(nx,ny)){sum++;dfs(nx,ny);}}
}
int main(){cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>a[i][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(a[i][j]=='@'){sum++;dfs(i,j);break;}}}cout<<sum;return 0;
}
相关文章:

算法知识-15-深搜
一、概念 深度优先搜索(Deep First Search, DFS)是一种用于遍历或搜索树或图的算法。这种策略沿着树的深度遍历树的节点,尽可能深地搜索树的分支。 二、关键步骤 选择起点:根据题目要求,选择一个或多个节点作为搜索…...
)
区块链dapp 开发详解(VUE3.0)
1、安装metamask 插件。 2、使用封装的工具包: wagmi . 3、 wagmi 操作手册地址:connect | Wagmi 4、注意事项: 因为最初是react 版本,所以在VUE版的官方文档有很多地方在 import 用的是 wagmi,需要改为 wagmi/vue 。 连接成功后打印的内容如下&…...

Plugin [id: ‘flutter‘] was not found in any of the following sources解决方法
文章目录 错误描述解决方法修正方案:继续使用 apply from修正后的 build.gradle说明警告的处理进一步验证 错误描述 Plugin [id: ‘flutter’] was not found in any of the following sources: Gradle Core Plugins (not a core plugin, please see https://docs…...

专升本-高数 1
第 0 章,基础知识 一,重要公式 1、完全平方 (ab)a2abb (a-b)a-2abb 2、平方差公式 (a-b)(ab)a-b 3、立方差公式 a-b(a-b)(aabb) 4、 立方和公式 ab(ab)(a-abb) 二,基本初等函数 1,幂函数 一元二…...

【考前预习】3.计算机网络—数据链路层
往期推荐 【考前预习】2.计算机网络—物理层-CSDN博客 【考前预习】1.计算机网络概述-CSDN博客 浅谈云原生--微服务、CICD、Serverless、服务网格_云原生cicd-CSDN博客 子网掩码、网络地址、广播地址、子网划分及计算_子网广播地址-CSDN博客 浅学React和JSX-CSDN博客 目录 1.数…...

DockeUI 弱口令登录漏洞+未授权信息泄露
0x01 产品描述: DockerUI是一款开源的、强大的、轻量级的Docker管理工具。DockerUI覆盖了 docker cli 命令行 95% 以上的命令功能,通过可视化的界面,即使是不熟悉docker命令的用户也可以非常方便的进行Docker和Docker Swarm集群进行管理和维护。0x02 漏洞描述: DockerUI中存…...

【电子元器件】电感基础知识
本文章是笔者整理的备忘笔记。希望在帮助自己温习避免遗忘的同时,也能帮助其他需要参考的朋友。如有谬误,欢迎大家进行指正。 一、 电感的基本工作原理 1. 电感的基本工作原理如下: (1) 当线圈中有电流通过时&#…...

【SSH+X11】VsCode使用Remote-SSH在远程服务器的docker中打开Rviz
🚀今天来分享一下通过VsCode的Remote-SSH插件在远程服务器的docker中打开Rviz进行可视化的方法。 具体流程如下图所示,在操作开始前,请先重启设备,排除之前运行配置的影响: ⭐️ 我这里是使用主机连接服务器ÿ…...
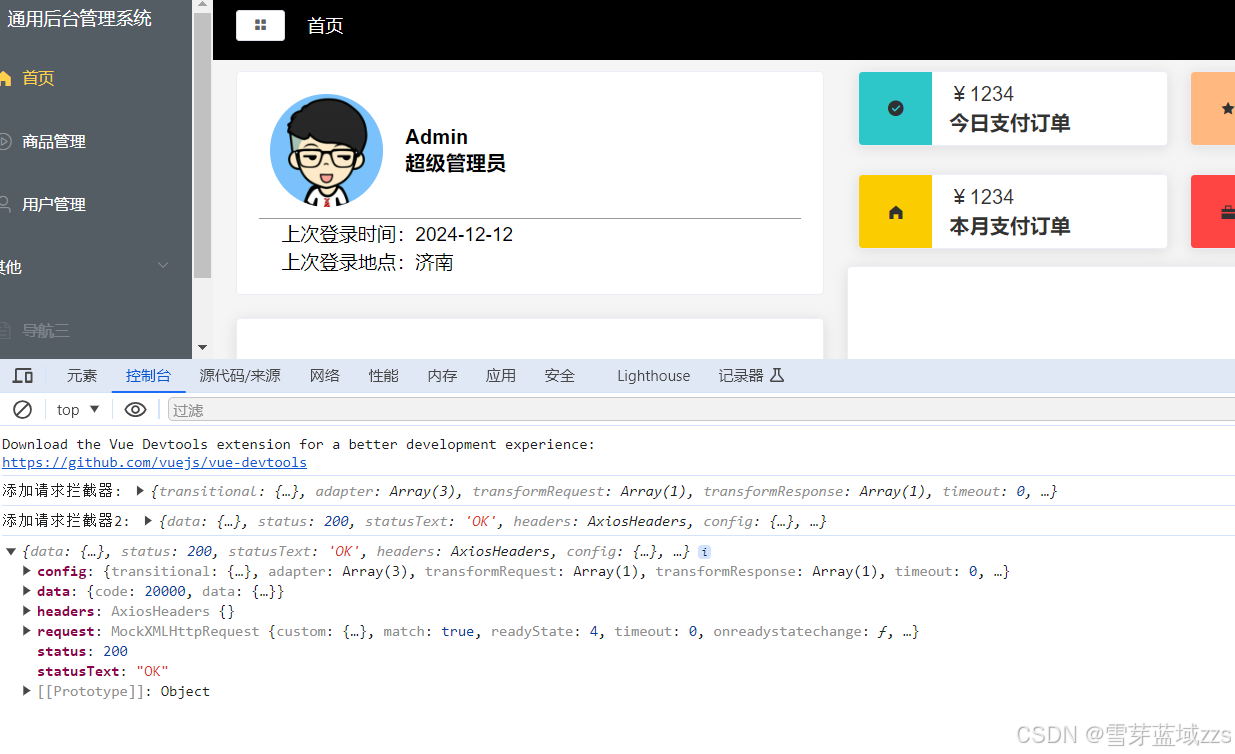
Vue Web开发(五)
1. axios axios官方文档 异步库axios和mockjs模拟后端数据,axios是一个基于promise的HTTP库,使用npm i axios。在main.js中引入,需要绑定在Vue的prototype属性上,并重命名。 (1)main.js文件引用 imp…...

HarmonyOS:使用Grid构建网格
一、概述 网格布局是由“行”和“列”分割的单元格所组成,通过指定“项目”所在的单元格做出各种各样的布局。网格布局具有较强的页面均分能力,子组件占比控制能力,是一种重要自适应布局,其使用场景有九宫格图片展示、日历、计算器…...
开源Java快速自测工具,可以调用系统内任意一个方法
java快速测试框架,可以调到系统内任意一个方法,告别写单测和controller的困扰。 开源地址:https://gitee.com/missyouch/Easy-JTest 我们在开发时很多时候想要测试下自己的代码,特别是service层或者是更底层的代码,就…...

力扣刷题TOP101: 29.BM36 判断是不是平衡二叉树
目录: 目的 思路 复杂度 记忆秘诀 python代码 目的: 输入一棵节点数为 n 二叉树,判断该二叉树是否是平衡二叉树。 思路 什么是平衡二叉树(AVL 树)? 每个节点的左子树和右子树的高度差不能超过 1。确保…...

【在Linux世界中追寻伟大的One Piece】自旋锁
目录 1 -> 概述 2 -> 原理 3 -> 优缺点及使用场景 3.1 -> 优点 3.2 -> 缺点 3.3 -> 使用场景 4 -> 纯软件自旋锁类似的原理实现 4.1 -> 结论 5 -> 样例代码 1 -> 概述 自旋锁是一种多线程同步机制,用于保护共享资源避免受并…...
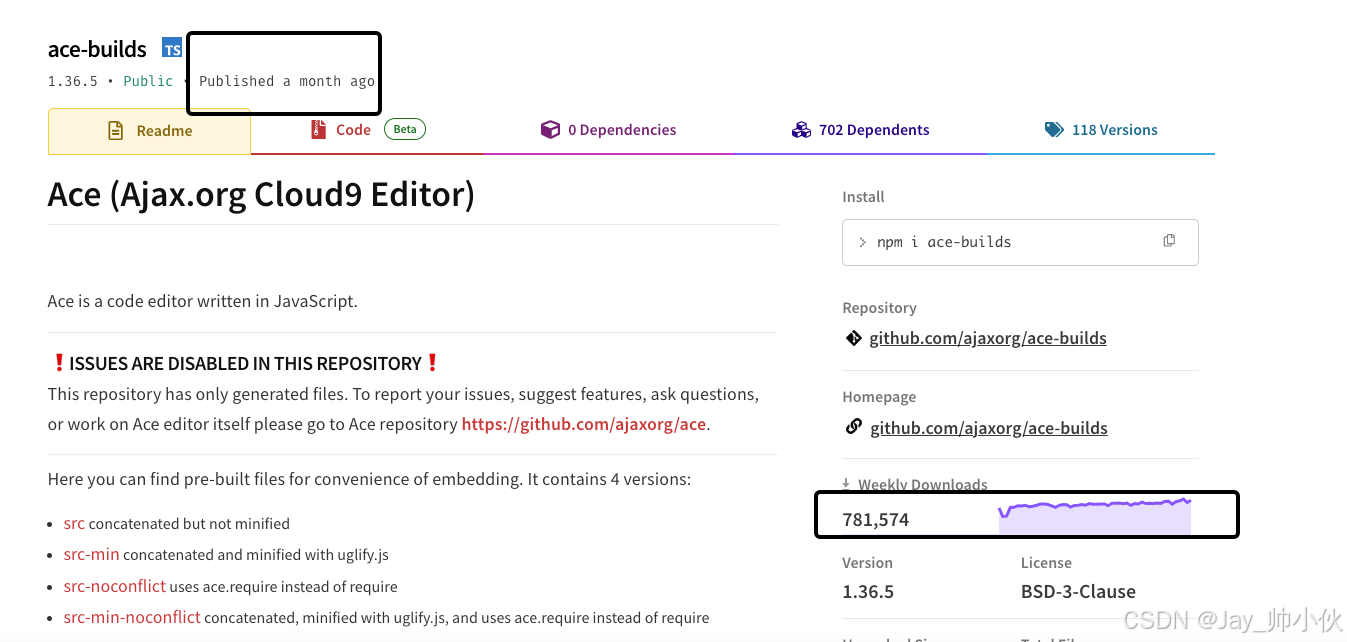
前端编辑器JSON HTML等,vue2-ace-editor,vue3-ace-editor
与框架无关 vue2-ace-editor有问题,ace拿不到(brace) 一些组件都是基于ace-builds或者brace包装的 不如直接用下面的,不如直接使用下面的 <template><div ref"editor" class"json-editor"><…...

C++ 中的运算符重载
运算符重载是C中的一种特性,它允许开发者为自定义类型定义或改变标准运算符的行为。通过运算符重载,你可以使得用户定义的类像内置类型一样使用运算符,比如加法、减法、赋值等。 如何在C中进行运算符重载? 重载运算符的语法&#…...

渗透测试工具 -- SQLmap安装教程及使用
随着网络安全问题日益严峻,渗透测试成为了保护信息安全的重要手段。而在渗透测试的众多工具中,SQLmap凭借其强大的自动化SQL注入检测和利用能力,成为了网络安全专家必备的利器。那么,你知道如何高效地使用SQLmap进行漏洞扫描吗&am…...
使用 Database Tools 实现高效数据查询的十大 IntelliJ IDEA 快捷键
得益于 IntelliJ IDEA Ultimate 的 Database Tools(数据库工具)中的专用 SQL 查询控制台,您无需离开 IDE 即可轻松修改连接到您的 Java 应用程序的任何数据库中的数据,以及从这些数据库中提取数据。 查询控制台具有 SQL 语句特定的…...
SpringBoot 整合 RabbitMQ 实现流量消峰
RabbitMQ 即一个消息队列,主要是用来实现应用程序的异步和解耦,同时也能起到消息缓冲,消息分发的作用。 消息中间件在互联网公司的使用中越来越多,刚才还看到新闻阿里将 RocketMQ 捐献给了 Apache,当然了今天的主角还…...

大数据挖掘建模平台案例分享
大数据挖掘建模平台是由泰迪自主研发,面向企业级用户的大数据挖掘建模平台。平台采用可视化操作方式,通过丰富内置算法,帮助用户快速、一站式地进行数据分析及挖掘建模,可应用于处理海量数据、高复杂性的数据挖掘任务,…...

MySQL数据表的管理
1.创建表 语法: create table 表名( 字段名 字段里保存数据的类型【(数据的长度) 约束】, 字段名 字段里保存数据的类型【(数据的长度) 约束】, 字段名 字段里保存数据的类型【(数据的长度) 约束】 ...... ); 注意:数据类型和约束,接下来用…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

13.10 LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析
LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析 LanguageMentor 对话式训练系统架构与实现 关键词:多轮对话系统设计、场景化提示工程、情感识别优化、LangGraph 状态管理、Ollama 私有化部署 1. 对话训练系统技术架构 采用四层架构实现高扩展性的对话训练…...

手动给中文分词和 直接用神经网络RNN做有什么区别
手动分词和基于神经网络(如 RNN)的自动分词在原理、实现方式和效果上有显著差异,以下是核心对比: 1. 实现原理对比 对比维度手动分词(规则 / 词典驱动)神经网络 RNN 分词(数据驱动)…...

python读取SQLite表个并生成pdf文件
代码用于创建含50列的SQLite数据库并插入500行随机浮点数据,随后读取数据,通过ReportLab生成横向PDF表格,包含格式化(两位小数)及表头、网格线等美观样式。 # 导入所需库 import sqlite3 # 用于操作…...

java+webstock
maven依赖 <dependency><groupId>org.java-websocket</groupId><artifactId>Java-WebSocket</artifactId><version>1.3.5</version></dependency><dependency><groupId>org.apache.tomcat.websocket</groupId&…...
