JavaScript ES6+ 语法速通
一、ES6 基础语法
1. let 和 const 声明变量
let:块级作用域,可以重新赋值。const:块级作用域,声明常量,不能重新赋值。
let name = 'Li Hua';
name = 'Li Ming'; // 可修改const age = 21;
// age = 22; // 报错,const 不能重新赋值
2. 模板字符串
使用反引号 `,支持 字符串插值 和 多行字符串。
const name = 'Li Hua';
const age = 21;const message = `Hello, my name is ${name}. I'm ${age} years old.`;
console.log(message);const multiLine = `这是一行
这又是另一行`;
console.log(multiLine);
3. 解构赋值
- 数组解构:
const [a, b, c] = [1, 2, 3];
console.log(a, b, c); // 1, 2, 3
- 对象解构:
const person = { name: 'Li Hua', age: 21 };
const { name, age } = person;
console.log(name, age); // 'Li Hua', 21
- 默认值:
const { city = 'Wuhan' } = {};
console.log(city); // 'Wuhan'
4. 箭头函数
箭头函数简化写法,并且不会绑定 this。
const sum = (a, b) => a + b;
console.log(sum(3, 4)); // 7const square = n => n * n;
console.log(square(5)); // 25
5. 扩展运算符 ...
- 数组展开:
const arr1 = [1, 2, 3];
const arr2 = [...arr1, 4, 5];
console.log(arr2); // [1, 2, 3, 4, 5]
- 对象合并:
const obj1 = { a: 1, b: 2 };
const obj2 = { ...obj1, c: 3 };
console.log(obj2); // { a: 1, b: 2, c: 3 }
- 函数参数:
function sum(...numbers) {return numbers.reduce((a, b) => a + b, 0);
}
console.log(sum(1, 2, 3, 4)); // 10
6. 默认参数
function greet(name = 'Guest') {console.log(`Hello, ${name}!`);
}
greet(); // 'Hello, Guest!'
greet('Li Hua'); // 'Hello, Li Hua!'
7. for…of 遍历
const arr = [1, 2, 3];
for (const num of arr) {console.log(num);
}
8. Promise 和异步操作
const fetchData = new Promise((resolve, reject) => {setTimeout(() => resolve('数据加载成功'), 2000);
});fetchData.then(data => console.log(data)).catch(err => console.log(err));
二、ES7+ 高级语法
1. ES7:includes 方法
const arr = [1, 2, 3];
console.log(arr.includes(2)); // true
console.log(arr.includes(5)); // false
2. ES8:Async/Await
function delay(ms) {return new Promise(resolve => setTimeout(resolve, ms));
}async function loadData() {console.log('开始加载...');await delay(2000);console.log('数据加载成功');
}loadData();
3. ES9:对象的 Rest 和 Spread
- Rest 参数:
const { a, ...rest } = { a: 1, b: 2, c: 3 };
console.log(rest); // { b: 2, c: 3 }
- 对象展开:
const obj = { ...{ a: 1 }, b: 2 };
console.log(obj); // { a: 1, b: 2 }
4. ES10:Optional Catch Binding
try {throw new Error('出错了');
} catch {console.log('捕获异常');
}
5. ES11:可选链操作符 ?.
const user = { name: 'Li Hua', address: { city: 'Wuhan' } };
console.log(user.address?.city); // 'Wuhan'
console.log(user.contact?.phone); // undefined
6. ES12:逻辑赋值运算符
let a = null;
a ??= 'default';
console.log(a); // 'default'let b = 5;
b &&= 10;
console.log(b); // 10
相关文章:

JavaScript ES6+ 语法速通
一、ES6 基础语法 1. let 和 const 声明变量 let:块级作用域,可以重新赋值。const:块级作用域,声明常量,不能重新赋值。 let name Li Hua; name Li Ming; // 可修改const age 21; // age 22; // 报错࿰…...

移动端h5自适应rem适配最佳方案
网页开发中,我们常用的单位有如下几个: px:像素固定,无法适配各分辨率的移动设备em: 该单位受父容器影响,大小为父元素的倍数rem: 因为html根元素大小为16px,所以默认 1rem 16px,rem只受根元素…...

2024年使用 Cython 加速 Python 的一些简单步骤
文章结尾有最新热度的文章,感兴趣的可以去看看。 本文是经过严格查阅相关权威文献和资料,形成的专业的可靠的内容。全文数据都有据可依,可回溯。特别申明:数据和资料已获得授权。本文内容,不涉及任何偏颇观点,用中立态度客观事实描述事情本身 文章有点长,期望您能坚持看…...

EasyExcel设置表头上面的那种大标题(前端传递来的大标题)
1、首先得先引用easyExcel的版本依赖,我那 <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>2.2.6</version> </dependency> 2、然后得弄直接的实体类,&…...

【Linux网络编程】第十弹---打造初级网络计算器:从协议设计到服务实现
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】【C详解】【Linux系统编程】【Linux网络编程】 目录 1、Protocol.hpp 1.1、Request类 1.1.1、基本结构 1.1.2、构造析构函数 1.1.3、序列化函数 1.1.4、反…...

无限弹窗?无限重启?
Windows开机自启目录: "%USERPROFILE%\AppData\Roaming\Microsoft\windows\StartMenu\Programs\Startup" 基于这个和 start 命令, shutdown 命令, 编写 bat 病毒程序。 无限弹窗 echo start cmd > hack.txt echo %0 >>…...

深入详解人工智能机器学习常见算法中的K-means聚类
目录 引言 1. K-means聚类的基本概念 1.1 K-means聚类的定义 1.2 K-means聚类的核心思想 1.3 K-means聚类的目标函数 2. K-means聚类的核心原理 2.1 初始化 2.2 分配 2.3 更新 2.4 迭代 3. K-means聚类的具体实现 3.1 K-means聚类的算法流程 3.2 K-means聚类的Pyt…...

lc146LRU缓存——模仿LinkedHashMap
146. LRU 缓存 - 力扣(LeetCode) 法1: 调用java现有的LinkedHashMap的方法,但不太理解反正都不需要扩容,super(capacity, 1F, true);不行吗,干嘛还弄个装载因子0.75还中途扩容一次浪费时间。 class LRUC…...

全面深入解析:C语言动态库
引言 动态库(Dynamic Library)是现代软件开发中不可或缺的一部分,它们不仅提高了代码的重用性和维护性,还显著提升了系统的性能和资源利用率。本文将全面探讨C语言中的动态库,从基础概念到高级应用,通过丰…...

运用 SSM 实现垃圾分类系统智能化升级
目 录 摘 要 1 前 言 3 第1章 概述 4 1.1 研究背景 4 1.2 研究目的 4 1.3 研究内容 4 第二章 开发技术介绍 5 2.1Java技术 6 2.2 Mysql数据库 6 2.3 B/S结构 7 2.4 SSM框架 8 第三章 系统分析 9 3.1 可行性分析 9 3.1.1 技术可行性 9 3.1.2 经济可行性 10 3.1.3 操作可行性 10 …...

LeNet-5:深度学习与卷积神经网络的里程碑
目录 编辑 引言 LeNet-5的结构与原理 输入层 C1层:卷积层 S2层:池化层 C3层:卷积层 S4层:池化层 C5层:卷积层 F6层:全连接层 输出层 LeNet-5的算法基础 LeNet-5的优点 LeNet-5的现代应用 …...

从资产流动分析WIF市场潜力X.game深究其他未知因素
近日,两则关于WIF最新消息引起了投资者们的注意。据报道,11月28日Vintermute在过去13小时内累计从Binance交易所提取了价值533万美元的WIF,此举不仅彰显了其强大的资金实力,更在某种程度上推动了WIF币价的反弹;另一方面…...

深入解析Vue3响应式系统:从Proxy实现到依赖收集的核心原理
深入解析Vue3响应式系统:从Proxy实现到依赖收集的核心原理 响应式系统的基本原理 作为一个热门的JavaScript框架,Vue在3.x版本中引入了基于Proxy的响应式系统。这个系统的核心思想是利用Proxy对象拦截对数据的访问和修改,从而实现数据的自动更…...

FPGA实现GTP光口数据回环传输,基于Aurora 8b/10b编解码架构,提供2套工程源码和技术支持
目录 1、前言工程概述免责声明 2、相关方案推荐我已有的所有工程源码总目录----方便你快速找到自己喜欢的项目我这里已有的 GT 高速接口解决方案 3、工程详细设计方案工程设计原理框图用户数据发送模块基于GTP高速接口的数据回环传输架构GTP IP 简介GTP 基本结构GTP 发送和接收…...

Linux网络 UDP socket
背景知识 我们知道, IP 地址用来标识互联网中唯一的一台主机, port 用来标识该主机上唯一的一个网络进程,IPPort 就能表示互联网中唯一的一个进程。所以通信的时候,本质是两个互联网进程代表人来进行通信,{srcIp&…...

如何持续优化呼叫中心大模型呼入机器人的性能?
如何持续优化呼叫中心大模型呼入机器人的性能? 原作者:开源呼叫中心FreeIPCC,其Github:https://github.com/lihaiya/freeipcc 持续优化呼叫中心大模型呼入机器人的性能是一个复杂而细致的过程,它涉及到数据、模型结构…...
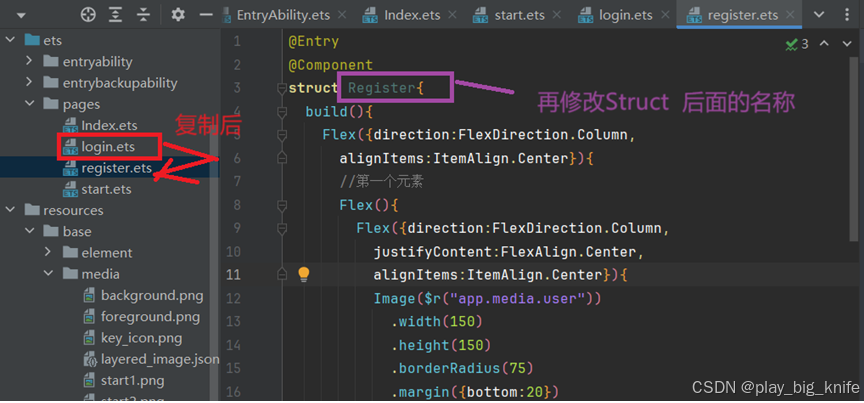
鸿蒙项目云捐助第四讲鸿蒙App应用的登陆注册页实现
根据app的操作流程可以知道,当启动页启动后,点击启动页中的页面就进入到了登录页。本讲就是针对于登录注册页的实现,实现的界面参考下图。 这里根据这个素材的参考实现鸿蒙Next云捐助的登录页。 一、鸿蒙Next云捐助登录页的实现 在项目中继…...

Windows本地搭建Redis集群(集群模式)
手打不易,如果转摘,请注明出处! 注明原文:https://blog.csdn.net/q258523454/article/details/144477957 前言 Redis版本:redis 5.0.14.1 Windows版本:Windows10 本文只讲集群模式 1. 安装Redis 1.1 …...

使用FastGPT制做一个AI网站日志分析器
越来越的多网站面临每天上千次的扫描和各类攻击,及时发现攻击IP,并有效的屏蔽不良访问成为网站安全的重要保障,这里我们使用AI来完成对网站日志的日常分析。 我们来使用FastGPT来制做一个AI网站日志析器,下面就开始: …...

探索 Echarts 绘图:数据可视化的奇妙之旅
目录 一、Echarts 初印象 二、搭建 Echarts 绘图环境 三、绘制第一个图表:柱状图的诞生 四、图表的美化与定制:让数据更具吸引力 1. 主题切换:一键变换风格 2. 颜色调整:色彩搭配的艺术 3. 标签与提示框:丰富信…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...
