代码随想录D22-23 回溯算法01-02 Python
理论回顾
回溯法也可以叫做回溯搜索法,它是一种搜索的方式。回溯是递归的副产品,只要有递归就会有回溯。
回溯的本质是穷举,穷举所有可能,然后选出我们想要的答案,如果想让回溯法高效一些,可以加一些剪枝的操作,但也改不了回溯法就是穷举的本质。
回溯法,一般可以解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
理解回溯
回溯法解决的问题都可以抽象为树形结构,是所有回溯法的问题都可以抽象为树形结构!
因为回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度就构成了树的深度。
递归就要有终止条件,所以必然是一棵高度有限的树(N叉树)。
回溯法模板
- 回溯函数模板返回值以及参数
- 回溯函数终止条件
- 回溯搜索的遍历过程
77. 组合

要点:
以暴搜为起点进行思考的话,搜索k为2时的结果可以使用两个嵌套for循环实现。将k拓展到大于2的数,可以发现用同样的思路解决问题就需要做k次嵌套的for循环。肯定无法解决本题的问题。
实际上,在回溯算法中,k次嵌套其实就是算法中递归的深度了,通过递归来解决不定次数的嵌套循环即可轻松解决。
解法:
树形结构:

输入输出:两个全局变量,一个用来存放符合条件单一结果,一个用来存放符合条件结果的集合。 两个参数,既然是集合n里面取k个数,那么n和k是两个int型的参数。然后还需要一个参数,为int型变量startIndex,这个参数用来记录本层递归的中,集合从哪里开始遍历
终止条件:到达满足输出要求(叶子节点)
单步逻辑:for循环每次从startIndex开始遍历,然后用path保存取到的节点i。
实现:
class Solution:def combine(self, n: int, k: int) -> List[List[int]]:# 创建所有结果的总表results = list()self.backtracking(n, k, 1, [], results)return resultsdef backtracking(self, n, k, start_idx, path, results):# 终止条件 当path长度达到了要求 表示已经深入到了叶子节点if len(path) == k:results.append(path[:])returnfor i in range(start_idx, n + 1):path.append(i)# 使用递归来完成等价多个for循环的嵌套self.backtracking(n, k, i + 1, path, results)# 回溯步 撤销本层的遍历结果path.pop()将for循环的右区间换成下面这个表达,就可以进行特定情况下的剪枝。含义是,已经选择的元素个数 len(path) ; 还需要的元素个数为: k - len(path),还需要选择的元素数量不能大于数组中剩余的数量。
for i in range(startIndex, n - (k - len(path)) + 2):pass216. 组合总和 III

要点:

转换成树形问题之后,可以观察到和组合的相似之处。遍历的宽度是确定值9个数,而深度则是k,目标值是n。
解法:
全局变量:依然需要一维数组path来存放符合条件的结果,二维数组result来存放结果集
输入输出:1. 目标和n;2. 数量k;3. 目标和sum;4. 起始索引start_idx
终止条件:path.size() 和 k相等了,就终止;
单步逻辑:添加一步总和累加和回溯减去即可
实现:
class Solution:def combinationSum3(self, k: int, n: int) -> List[List[int]]:results = list()self.backtracking(n, k, 0, 1, [], results)return resultsdef backtracking(self, tar_sum, num_count, cur_sum, start_idx, path, results):if cur_sum > tar_sum:returnif len(path) == num_count:if cur_sum == tar_sum:results.append(path[:])returnfor i in range(start_idx, 9 - (num_count - len(path)) + 2):path.append(i)cur_sum += iself.backtracking(tar_sum, num_count, cur_sum, i + 1, path, results)cur_sum -= ipath.pop()17. 电话号码的字母组合

要点:
一个数字会对应多个字母,可能出现多个数字。因此,这里需要一个index来指向正在遍历的数字。
实现:
class Solution:def __init__(self):self.letterMap = ["", # 0"", # 1"abc", # 2"def", # 3"ghi", # 4"jkl", # 5"mno", # 6"pqrs", # 7"tuv", # 8"wxyz" # 9]self.result = []def get_comb(self, digits, idx, sub_res):# 当索引和数字总长一致时,添加字母结果并返回if idx == len(digits):self.result.append(sub_res)return# 通过数字取字母数组letter_str = self.letterMap[int(digits[idx])]# 通过for循环将每个数组中的结果依次加入子结果for letter in letter_str:self.get_comb(digits, idx + 1, sub_res + letter)def letterCombinations(self, digits: str) -> List[str]:if len(digits) == 0:return []self.get_comb(digits, 0, '')return self.result39. 组合总和

要点:
本题没有数量要求,可以无限重复,但是有总和的限制,所以间接的也是有个数的限制。终止条件则应设定为超过目标值则判断并返回。

解法:
全局变量:一个sub_res存放单个path,一个results存放所有结果
输入输出:和组合总和基本类似,原始数组,目标值,记录一个当前值总和,开始索引,分支结果和全部结果。
和之前的不同在于,在backtrack中,将start_idx设置成当前循环索引,即不用额外做i+1。
实现:
class Solution:def backtrack(self, candidates, target, cur_sum, start_idx, sub_res, results):if cur_sum > target:returnif cur_sum == target:results.append(sub_res[:])return for i in range(start_idx, len(candidates)):cur_sum += candidates[i]sub_res.append(candidates[i])# 之前使用了i + 1 这里直接从i开始表示可以重复使用self.backtrack(candidates, target, cur_sum, i, sub_res, results)cur_sum -= candidates[i]sub_res.pop()def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:results = []self.backtrack(candidates, target, 0, 0, [], results)return results40. 组合总和 II

要点:
这里指定了每个数字只能使用一次,数组candidates的元素是有重复的,且解集中不能有重复结果。
在回溯中的去重,本质就是使用过的元素不能重复选取。 已知组合问题可以抽象为树形结构,那么“使用过”在这个树形结构上是有两个维度的,一个维度是同一树枝上使用过,一个维度是同一树层上使用过。没有理解这两个层面上的“使用过” 会导致不能彻底理解去重。

转换成树形结构可以总结,元素在同一个组合内是可以重复的,怎么重复都没事,但两个组合不能相同。所以我们要去重的是同一树层上的“使用过”,同一树枝上的都是一个组合里的元素,不用去重。
想要进行树层的去重,首先需要对候选数组进行一次排序。除此之外,此题还需要加一个bool型数组used,来记录每个元素的使用情况。最核心的理解在于回溯中的递归,以上图为例,假设在第一个分支里已经取过了第二个1,那么在第二个分支中应该忽略掉连续取两个1的情况,因为同样的结果已经出现在了第一个递归的分支中。
- used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
- used[i - 1] == false,说明同一树层candidates[i - 1]使用过
这里就体现了排序的必要性,只有先进行排序才能确保:只对前一位的使用情况进行判断就能够去除所有重复;大小颠倒的组合情况被自然消除了。
解法:
输入参数:输入数组,目标数值,总和,起始索引,已使用元素记录,单条路径,最终结果
终止条件:达到target返回,遇到重复或超过目标值分别跳过和停止递归
单步逻辑:按照上述描述进行去重,传入新的startindex,进行递归计算
实现:
class Solution:def backtrack(self, candidates, target, total, start_idx, used, path, result):if total == target:result.append(path[:])returnfor i in range(start_idx, len(candidates)):# 去重逻辑 只去除相同数字 且上一个相同数字没用的情况if i > start_idx and candidates[i] == candidates[i - 1] and not used[i - 1]:continue# if total > target:break# 三个变量依次修改total += candidates[i]path.append(candidates[i])used[i] = True# 从i + 1开始 保证正确递归顺序self.backtrack(candidates, target, total, i + 1, used, path, result)used[i] = Falsepath.pop()total -= candidates[i]def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:used = [False] * len(candidates)result = []candidates.sort()self.backtrack(candidates, target, 0, 0, used, [], result)return result131. 分割回文串

要点:
这里提出了需要返回所有可能的分割方案,观察可得所谓的分割,其实也是一种组合问题。
例如对于字符串abcdef:
- 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中再选取第三个。
- 切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中再切割第三段。
所以此类切割的问题可以转换成树形问题

解法:
输入输出:本题递归函数参数还需要startIndex,因为切割过的地方,不能重复切割,和组合问题也是保持一致的。
单步逻辑:递归循环中如何截取子串?在一个子循环中,我们 定义了起始位置startIndex,那么 [startIndex, i] 就是要截取的子串。和组合问题一致。在单步过程中判断每次切割出的子串是不是回文字串。如果是,那么进行下一步递归。
终止条件:当i已经是最后一位,则停止
实现:
class Solution:def backtrack(self, s, start_idx, path, results):if start_idx == len(s):results.append(path[:])returnfor i in range(start_idx, len(s)):## 右侧需要从start的下一位开始 遵循python切片左闭右开if s[start_idx: i+1] == s[start_idx: i+1][::-1]:path.append(s[start_idx: i+1])self.backtrack(s, i + 1, path, results)path.pop()def partition(self, s: str) -> List[List[str]]:results = list()self.backtrack(s, 0, [], results)return results相关文章:

代码随想录D22-23 回溯算法01-02 Python
理论回顾 回溯法也可以叫做回溯搜索法,它是一种搜索的方式。回溯是递归的副产品,只要有递归就会有回溯。 回溯的本质是穷举,穷举所有可能,然后选出我们想要的答案,如果想让回溯法高效一些,可以加一些剪枝…...

【网络云计算】2024第50周-每日【2024/12/13】小测-理论-写10个Bash Shell脚本-解析
文章目录 1. 计算1到100的和2. 列出当前目录下所有文件和文件夹3. 检查文件是否存在4. 备份文件到指定目录(简单示例)5. 打印系统当前日期和时间6. 统计文件中的行数7. 批量重命名文件(将.txt后缀改为.bak)8. 查找进程并杀死&…...
FFT 和 IFFT 的缩放因子)
MATLAB转换C语言--问题(一)FFT 和 IFFT 的缩放因子
1. MATLAB 中的 FFT 和 IFFT 在 MATLAB 中,fft 和 ifft 函数具有以下缩放行为: fft:执行快速傅里叶变换(FFT),不进行缩放。ifft:执行逆快速傅里叶变换(IFFT),…...
轻松上手:使用 Vercel 部署 HTML 页面教程
😀 在学习前端的过程中,部署项目往往是一个令人头疼的问题。然而,Vercel 为我们提供了一个便捷且免费的解决方案。 Vercel 是一个强大的云平台,专门用于前端项目的部署和托管。它不仅支持多种前端框架和静态网站生成器࿰…...

如何运用 HTM?
一、HTM 概述 HTM(Hierarchical Temporal Memory,分层时序记忆)是一种基于神经科学原理构建的计算模型,旨在模拟大脑的学习和记忆机制,以处理复杂的时间序列数据和模式识别任务。它具有独特的架构和算法,能…...

12.16【net】【study】
路由表是路由器或者其他互联网网络设备上存储的一张表,它记录了到达特定网络目的地的路径。路由表中的每一行(即一个路由条目)包含了目的地网络地址、子网掩码、下一跳地址、出接口等信息。 Destinations(目的地)和 R…...

2023和2024历年美赛数学建模赛题,算法模型分析!
文末获取历年优秀论文解析,可交流解答 2023年题目分析 MCM(Mathematical Contest in Modeling) 问题 A:遭受旱灾的植物群落 概述:要求建立预测模型,模拟植物群落在干旱和降水充裕条件下随时间的变化。类…...

Node.js内置模块
1.内置模块 Node.js的中文网参考手册:https://nodejs.cn//api 帮助文档 API文档:查看对应的模块,左边是模块,右边是模块的成员 源码:https://github.com/nodejs/node/tree/main/lib 查看 例如: http.js 创建web服务器的模块 -->进入源码中,搜索…...

测评|携程集团25年社招在线测评北森题库、真题分析、考试攻略
携程集团社招入职测评北森题库主要考察以下几个方面: 1. **言语理解**:这部分主要测试应聘者运用语言文字进行思考和交流、迅速准确地理解和把握文段要旨的能力。 2. **资料分析**:包括文字题和图表题,考察应聘者快速找出关键信息…...

快速启动Go-Admin(Gin + Vue3 + Element UI)脚手架管理系统
Go-Admin 是一个基于 Gin Vue Element UI & Arco Design & Ant Design 的前后端分离权限管理系统脚手架。它包含了多租户支持、基础用户管理功能、JWT 鉴权、代码生成器、RBAC 资源控制、表单构建、定时任务等功能。该项目的主要编程语言是 Go 和 JavaScript。 ps&a…...

数据分流:优化数据处理流程的关键策略
引言 在大数据时代,企业面临着数据量的激增和数据类型的多样化。为了有效地管理和分析这些数据,数据分流成为了一个重要的策略。数据分流指的是将数据按照特定的规则和流程分配到不同的处理路径,以优化数据处理效率和准确性。本文将探讨数据…...

RabbitMQ如何构建集群?
大家好,我是锋哥。今天分享关于【RabbitMQ如何构建集群?】面试题。希望对大家有帮助; RabbitMQ如何构建集群? 1000道 互联网大厂Java工程师 精选面试题-Java资源分享网 在RabbitMQ中,集群(Cluster&#x…...

RNN LSTM Seq2Seq Attention
非端到端: data -》 cleaning -》 feature Engining (70%-80%工作 设计特征)-》 分类器 -》预测 端到端 End-to-End: data -》 cleaning -》Deep learning(表示学习,从数据中学习特征) -》…...

硬件设计-ADC和低本底噪声为何至关重要
简介 在工程领域,精度是核心要素。无论是对先进电子设备执行质量和性能检测,还是对复杂系统进行调试,测量精度的高低都直接关系到项目的成功与否。这时,示波器中的垂直精度概念就显得尤为重要,它衡量的是电压与实际被…...

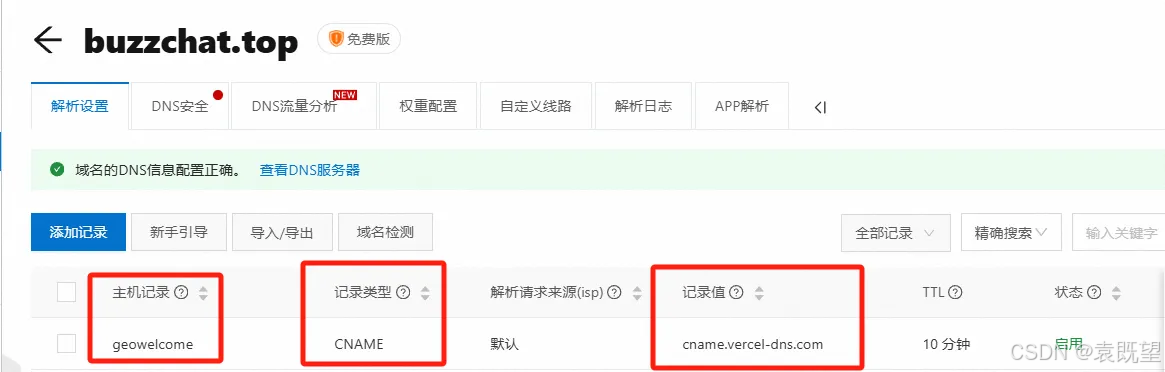
个性化域名配置
1 申请免费SSL证书 访问 https://certbot.eff.org ,可申请 通配符证书,每次申请可以使用3个月,到期可以免费续期。 2 配置nginx server index.conf 配置如下: server {listen 80;server_name biwow.com www.biwow.com;return …...

uniapp中打包应用后,组件在微信小程序和其他平台实现不同的样式
今天,我们来介绍一下,uniapp中如何实现打包应用后,组件在微信小程序和其他平台不同的样式,在这里,我们使用背景颜色进行演示,使用 UniApp 提供的 uni.getSystemInfoSync() 方法来获取系统信息,包…...

MRI脑肿瘤检测数据集,使用500张原始图片标注,支持yolo,coco,voc格式
MRI脑肿瘤检测数据集,使用500张原始图片标注,支持yolo,coco,voc格式 数据集下载: https://download.csdn.net/download/pbymw8iwm/90125474 https://download.csdn.net/download/pbymw8iwm/90125473 https://downl…...

JumpServer开源堡垒机搭建及使用
目录 一,产品介绍 二,功能介绍 三,系统架构 3.1 应用架构 3.2 组件说明 3.3 逻辑架构 3.3 逻辑架构 四,linux单机部署及方式选择 4.1 操作系统要求(JumpServer-v3系列版本) 4.1.1 数据库 4.1.3创建数据库参考 4.2 在线安装 4.2.1 环境访问 4.3 基于docker容…...
)
Java 编程旅程(二)
在前一篇博客中,我们介绍了 Java 编程的基础知识和入门步骤。现在,我们将继续深入探讨 Java 的一些高级特性,以帮助你进一步提升编程技能。通过这篇博客,你将学习到更复杂的概念和技术,比如面向对象编程(OO…...

一、springcloud 入门——笔记
1. 学习之前要知道的 springcloud 应用的技术 2. springboot 和 springcloud 的版本选型 官网介绍:https://spring.io/projects/spring-cloud/#overview 生成新的Spring Cloud项目 最简单的入门方法是访问start.spring.io,选择您的Spring Boot版本和要使…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...
