【图像处理lec3、4】空间域的图像增强
目录
1. 空间域图像增强的背景与目标
2. 空间域处理的数学描述
3. 灰度级变换
4. 幂律变换(Power-Law Transformation)
5、 分段线性变换
Case 1: 对比度拉伸
Case 2: 灰度切片
Case 3: 按位切片
6、对数变换(Logarithmic Transformation)
7、对比度拉伸(Contrast-Stretching Transformation)
8、直方图均衡
(1)直方图的定义
(2)直方图归一化
(3)直方图生成与显示
(4)直方图的对比分析
(5)代码示例
(6)直方图均衡化
i、目标:
ii、概率密度函数 (PDF) 和累计分布函数 (CDF)
iii、直方图均衡的变换函数
iv、离散版本的直方图均衡
9、直方图匹配
(1)原理概述
(2)直方图匹配的步骤
Step 1: 计算输入图像的累积分布函数 (CDF)
Step 2: 计算目标图像的累积分布函数 (CDF)
Step 3: 建立映射关系
Step 4: 应用映射
(3)示例
10、线性空间滤波
11、图像锐化
(1)锐化空间滤波的基本概念
(2)拉普拉斯滤波
(3)高提升滤波(High-Boost Filtering)
(4)图像梯度的计算与Sobel算子
12、非线性空间滤波
(1)定义与特点
(2)MATLAB工具箱中的非线性滤波
(3)具体实现与矩阵操作
13、非线性空间滤波去噪(去除椒盐噪声)
(1)非线性空间滤波工具 ordfilt2
(2)中值滤波器 medfilt2
(3)中值滤波的去噪效果对比
1. 空间域图像增强的背景与目标
- 图像增强的目标:通过处理图像使其对特定应用更适合。这里强调“特定应用”是问题导向的,因此增强方法没有统一的理论标准。
- 分类:
- 空间域方法:直接操作图像的像素。
- 频域方法:基于傅里叶变换的操作。
- 图像处理的评价:
- 对于视觉感知,评价取决于人类观察效果。
- 对于机器感知,如字符识别,评价通过任务完成度衡量。
2. 空间域处理的数学描述
- 数学表达式:
,其中
是一个操作符,可作用于像素的某个邻域。
- 邻域选择:通常使用方形或矩形邻域,因其易于实现。
- 最简单形式为强度变换,表示为
,即像素值的变换。
3. 灰度级变换

- 作用:调整图像像素值以实现增强效果。
- 示例中展示了不同的变换函数(例如S型和阶梯型),对应灰度范围从暗到亮的不同映射。
- 效果:调整对比度或强调特定灰度范围。
4. 幂律变换(Power-Law Transformation)

- 数学公式:
,通过调节
控制对比度。

- 典型应用:
- Gamma校正:用于显示器的线性响应矫正。
- 对比度增强:通过不同
值调整图像的细节和亮度。
- 下图展示了在医疗图像和航空图像中,通过不同的
值实现对比增强效果。


5、 分段线性变换
Case 1: 对比度拉伸

- 内容:图像的对比度拉伸通过增强低对比度区域来提高图像的视觉质量。
- 方法:
- 输入灰度值
与输出灰度值
之间建立分段线性关系。
- 拉伸低对比度部分(通过设定阈值
)。
- 示例:在原始低对比度图像上应用对比度拉伸,明显提高了对比度,增强了视觉效果。
- 输入灰度值
Case 2: 灰度切片

- 内容:通过灰度切片方法突出特定灰度范围的特性。
- 方法:
- 两种形式:将感兴趣的灰度范围值保留,其他灰度值置为常数;或保留所有灰度值,但突出特定范围。
- 应用:医学影像中,突出特定组织或结构。
Case 3: 按位切片

- 内容:按位切片以分离图像的不同比特平面。
- 方法:
- 图像由 8 个位平面组成,从最不重要位 (LSB) 到最重要位 (MSB)。
- 应用:观察 MSB 可以捕获主要图像结构,LSB 常用于存储隐藏数据(如水印)。


6、图像处理工具箱中的函数 imadjust
- 功能:
imadjust是 MATLAB 的图像处理工具箱中用于调整图像强度值分布的函数。 - 语法:
g = imadjust(f, [low_in high_in], [low_out high_out], gamma)- 参数解释:
low_in, high_in:输入强度值的范围。low_out, high_out:映射到的输出强度值范围。gamma:控制曲线的非线性程度。
- 参数解释:
- 特点:
gamma < 1:增强较暗区域的亮度。gamma > 1:增强较亮区域的亮度。- 默认情况下,
gamma = 1表示线性映射。

- 示例:
- 通过不同的参数组合调整乳腺图像对比度,以更清晰地观察病变区域。


图1左侧是从一个乳腺影像文件(Fig0303(a)(breast).tif)读取的,使用 imshow(I) 显示该图像,显示的是原始未处理的乳腺 X 光片。
图1右侧使用 G = imadjust(I, [0 1], [1 0]) 对原始图像进行处理,这种调整会产生一个负片效果,即原本亮的区域变暗,暗的区域变亮,显示负片的目的是强调图像中原本不明显的结构特征,方便分析。
图2左侧:对部分强度范围增强
- 使用
G = imadjust(I, [0.5 0.75], [0 1])。 - 参数
[0.5 0.75]选择了图像输入强度值的中间部分进行增强(从 0.5 到 0.75 的灰度范围)。 - 输出
[0 1]将这些强度范围映射到全新的灰度范围,增强了这一范围的对比度。 - 结果是更强烈的对比,突出原图中特定强度范围的细节。
图2右侧:伽马变换增强
- 使用
G = imadjust(I, [], [], 2)。 - 参数
[]表示默认的输入强度范围[0 1]和输出强度范围[0 1],2是伽马值。 - 伽马值为 2 表示对暗部区域的灰度值进行放大(权重偏向暗部区域),使得暗部区域的细节更加清晰。
- 用于强调图像中的低灰度特征。
6、对数变换(Logarithmic Transformation)
- 目的:压缩动态范围。对数变换常用于处理动态范围较大的图像数据,例如傅里叶频谱图。
- 公式:
,其中
是常数。
- 用途:
- 压缩高动态范围数据,例如从
压缩到较小范围。
- 通过 MATLAB 中的命令实现,例如
g = im2uint8(mat2gray(log(1 + double(f))))。
- 压缩高动态范围数据,例如从
- 例子:傅里叶频谱图

7、对比度拉伸(Contrast-Stretching Transformation)
- 公式:
,其中
为强度阈值,
控制函数的斜率。

- 作用:
- 将较低或较高的输入灰度值压缩到更窄的范围。
- 提高图像对比度,尤其适合灰度值分布范围有限的图像。
- MATLAB 实现:通过对应的公式,使用
double数据类型进行计算。
8、直方图均衡
(1)直方图的定义
- 图像的直方图是强度值的分布统计,是增强、压缩、分割和描述等图像处理操作的基础。
,其中:
:第
个强度值;
:强度值为
的像素数量。
(2)直方图归一化
- 通过归一化直方图,可以将像素数量转化为概率分布:
这里
是总像素数。直方图归一化可以表示为灰度值强度的概率估计。
(3)直方图生成与显示
- 使用 MATLAB 函数
imhist和bar绘制直方图:imhist(f, b):计算直方图,是灰度级分箱的数量。
bar(horz, h1, width):绘制条形图,其中horz为横轴刻度,h1为直方图数据。
(4)直方图的对比分析
- 直方图可以帮助可视化图像的亮度分布。例如:
- 暗图像的直方图主要集中在灰度较低的部分;
- 亮图像的直方图主要集中在灰度较高的部分。

(5)代码示例
生成直方图:
f = imread('Fig3_8_a.tif');
h = imhist(f);
bar(h);

绘制条形直方图:
s = imread('Fig0303(a).tif');
h1 = imhist(s, 16);
horz = 1:16;
bar(horz, h1, 0.8);

(6)直方图均衡化
i、目标:
- 增强图像的对比度。
- 将图像的灰度分布调整为近似均匀分布。
ii、概率密度函数 (PDF) 和累计分布函数 (CDF)
-
PDF(概率密度函数):
- 图像中每个灰度级的出现概率。
- 定义为:
其中:
是灰度级,
是灰度级
的像素个数,
- N 是总像素数。
-
CDF(累计分布函数):
- 累计分布函数是 PDF 的积分,用来表示灰度值从最小到当前灰度值的累计概率:
或连续形式:
累计分布函数的值范围是 [0,1]。
- 累计分布函数是 PDF 的积分,用来表示灰度值从最小到当前灰度值的累计概率:
iii、直方图均衡的变换函数
直方图均衡的变换函数恰好就是累计分布函数:
变换函数被定义为原始灰度级概率密度函数的累积分布函数 :
其中 是积分的中间变量,代表从 0 到
的所有灰度级,
是变换后的灰度值,是近似均匀分布的。
本质:将原图像的灰度级 按上述累积分布函数映射为新的灰度级
。这个过程实现了原始灰度分布到均匀分布的调整,最终得到对比度均衡化的图像。
定性理解:原灰度值比较集中的区域,概率密度比较大,概率密度的累计函数增长比较快,从而使得较短的就灰度值区域转换为较长的新的灰度值区域,即让原灰度值集中的区域分散;而原灰度值比较分散的区域,概率密度比较小,概率密度的累计函数增长缓慢,使得较长的原灰度值区域被转换为角度的新灰度值区域,即让原灰度值分散的区域集中。
证明新的灰度值分布 s 服从均匀分布:
推导新的概率密度函数 ,
的定义为:
- 根据变换
的定义(
),求导得:
- 代入
的表达式:
- 结论: 经过变换后,新的灰度级概率密度函数
是均匀分布,满足直方图均衡化目标。
iv、离散版本的直方图均衡
-
在实际实现中,图像是离散的,其灰度级的概率密度可以表示为:
其中
是灰度级
的像素数量,
是图像总像素数。
-
累积分布函数的离散形式为:
这意味着每个像素的新的灰度级
由其对应的累积概率决定。
9、直方图匹配
直方图匹配(Histogram Matching 或 Histogram Specification)是一种图像处理技术,其目标是将输入图像的直方图调整为目标图像或目标直方图的分布。相比于直方图均衡化,直方图匹配允许更灵活地调整图像的灰度分布,以适应特定需求。
(1)原理概述
直方图匹配的核心是将输入图像 的灰度级分布调整为与目标图像
的灰度级分布相同。
- 输入图像直方图:
,表示输入图像中灰度级
的概率分布。
- 目标直方图:
,表示目标图像中灰度级
的概率分布。
通过设计一个映射函数 ,使得调整后的灰度分布
匹配目标直方图。
(2)直方图匹配的步骤
Step 1: 计算输入图像的累积分布函数 (CDF)
输入图像灰度级 的累积分布函数定义为:
或者在离散情况下:
其中:
是灰度级
的像素数量。
是图像总像素数。
是原始概率密度
到均匀分布的映射。
Step 2: 计算目标图像的累积分布函数 (CDF)
目标图像灰度级 的累积分布函数定义为:
或者在离散情况下:
其中:
是目标直方图中灰度级
的像素数量。
是目标图像的总像素数(或者是目标直方图的总和)。
是目标图像灰度值概率密度
到均匀分布的映射;
是均匀分布到目标图像灰度值概率密度
的映射。而这里的均匀分布如果采用映射
的输出,那么就实现了原图灰度值概率密度
到目标图概率密度
的转换。
Step 3: 建立映射关系
输入图像中每个灰度值 的对应映射
满足:
,这两个映射的结果都是均匀分布,所以相等。
通过求解 ,找到
到
的映射关系。
- 在离散情况下,通过最近邻法或插值找到
与
的对应关系:
Step 4: 应用映射
对输入图像的每个像素值 ,通过上述映射关系
替换其值,最终获得直方图匹配后的图像。
(3)示例
直方图均衡:


- 输入图像(左侧的图)是 Mars 月亮 Phobos 的图片。
- 使用默认的 256-bin 直方图进行均衡,发现输出结果(右侧的图)不理想。
- 其原因是原始图像的像素值主要集中在低灰度区,导致均衡后产生大量离散化的高灰度值。
改进:直方图匹配:
-
为了解决上述问题,可以引入**双峰高斯模型(Bimodal Gaussian Model)**作为目标直方图,使其更符合原始图像的分布特性:
:两个高斯分布的均值。
:标准差。
:两个分布的权重。
-
通过指定该模型,生成一个平滑的目标直方图,应用到图像后得到更好的视觉效果。
最终结果:
通过调整目标直方图的形状,输出图像的灰度分布变得更加均匀,细节对比度增强。

10、线性空间滤波
定义与概念: 线性滤波使用固定大小的核(如3x3或5x5)滑动整个图像,对每个像素点应用线性运算。
- 公式:
其中,
是权值矩阵,
是输入图像。
- 滤波模式:
- 平滑滤波器(如平均滤波、加权平均滤波)。
- 卷积与相关的差别:卷积需要将核旋转180度。
- 使用函数: MATLAB函数
imfilter允许使用边界处理选项(replicate、symmetric、circular),支持对边界问题灵活处理。
均值滤波器
- 如Box滤波器(简单平均)和加权平均滤波器,常用于图像去噪或模糊化。
- 示例中,均值滤波器的掩模可以是:
或
锐化滤波
下面右有详细的分析。
11、图像锐化
(1)锐化空间滤波的基本概念
锐化的目标是突出图像中的细节或增强被模糊的特征,这通过空间微分(spatial differentiation)实现。
一阶导数的要求
一阶导数反映图像的边缘和灰度变化情况,满足以下条件:
- 在平坦区域(常量灰度区域)为零。
- 在灰度跳变的起始处非零。
- 在渐变区域非零。
数学表达:
二阶导数的要求
二阶导数有助于更精确地定位边缘和变化点,满足以下条件:
- 在平坦区域为零。
- 在灰度跳变的起始和结束处非零。
- 在渐变区域(常量斜坡)为零。
数学表达:
(2)拉普拉斯滤波
拉普拉斯滤波是一种二阶导数滤波器,通过计算图像中每个像素周围灰度变化的加权和来突出边缘。
拉普拉斯函数
二维拉普拉斯算子定义为:
离散实现为:
Laplacian 3×3 滤波模板
-
常用的拉普拉斯模板具有中心系数为负值、周围为正值的结构:
- 弱锐化模板:中心 −4,周围(上下左右)为 +1 ,四角(左上、右上、左下、右下)为0。
- 强锐化模板:中心 −8,周围(上下左右、左上、右上、左下、右下)为 +1 。
- 弱锐化滤波和强锐化滤波示例如下图:

-
在图中示例中,使用拉普拉斯滤波器对月球图像进行锐化,效果如下:
- 左上图:原始图像。
- 右上图:拉普拉斯滤波响应图(包含边缘信息)。
- 左下图:拉普拉斯滤波后的结果。
- 右下图:通过将拉普拉斯图像从原始图像中减去,实现锐化增强。

图像增强表达式
其中 是锐化后的图像,
是输入图像。
第一步是通过滤波器提取边缘信息,第二步是将边缘信息与原图像融合。这两步可以合在一起:
两步融合之后的滤波器核为:

(3)高提升滤波(High-Boost Filtering)
高提升滤波是一种基于非锐化掩模(Unsharp Masking)的扩展方法。它通过放大原始图像与模糊图像之间的差异实现锐化。
数学表达
- 非锐化掩模:
其中 是模糊后的图像,
是锐化后的图像。
- 高提升滤波:
进一步展开为:
当 时,退化为普通的非锐化掩模。
结合拉普拉斯的高提升滤波
如果拉普拉斯算子用于计算锐化掩模,则高提升滤波的公式变为:
或
图像示例分析

- 使用不同
值进行高提升滤波,
产生基本锐化效果,
提供更强烈的锐化。这里其实就是原图与锐化细节融合时减少了原图的权重,使得锐化更加凸显;但这样使得变化后的图像色度减弱了,如果不想色度减弱,就保持原图的权重为1,增大锐化细节的分量。
- 对比图展示了不同
值下的效果,高
值更突出边缘和细节。
(4)图像梯度的计算与Sobel算子
-
图像梯度的基本原理:
- 通过计算图像的一阶导数(梯度)来突出灰度值的变化,用于边缘检测和图像锐化。
- 梯度运算使用微分算子,包括Sobel算子和Prewitt算子,其系数矩阵如图1所示:
- 这些算子通过卷积操作提取图像边缘信息。
- Sobel算子(图2右图)增强了边缘对比度,有效检测边缘。


-
梯度增强效果:
- 左图(光学镜片)表现为平滑图像,右图为通过Sobel梯度算子计算得到的增强图像,显示了边缘和缺陷(4点和5点钟方向)。
- Sobel算子能够有效地检测图像中的轮廓信息,并放大边缘细节。
12、非线性空间滤波
(1)定义与特点
- 通常基于像素的局部邻域,但不像线性滤波那样应用固定的线性权值运算,而是使用其他数学操作(如取最大值、最小值、中值等)。
- 主要特点:
- 输出像素值由局部邻域的非线性操作确定(例如,局部最大值操作)。
- 与线性滤波不同,非线性滤波中“滤波核(mask)”的概念并不是必须的。
- 非线性滤波更加灵活,能更好地保留边缘等细节特性。
(2)MATLAB工具箱中的非线性滤波
片子中提到了两种主要函数:nlfilter 和 colfilt。
nlfilter(非线性空间滤波器)- 在二维图像上直接执行非线性操作。
- 用户可通过打开
nlfilter查看其源码。 - 缺点:计算效率相对较低。
colfilt(列过滤器)- 将数据以列的形式组织成矩阵,然后在每一列上执行操作。
- 内存占用较高,但执行速度快于
nlfilter。 - 数据结构组织后,结果更高效,但需要为大规模处理分配更多内存。
片子中的非线性空间滤波主要内容及分析如下:
(3)具体实现与矩阵操作
colfilt 函数原理
- 输入:
- 图像
的大小为
。
- 滤波窗口的大小为
。
- 图像
- 输出:
- 将图像滑动窗口生成一个矩阵
,大小为
,每一列表示图像中邻域窗口的像素。
- 将图像滑动窗口生成一个矩阵
- 特点:
- 每一列包含一个邻域窗口的像素数据,方便应用非线性函数对每一列进行单独操作。
colfilt 的函数语法:
-
参数说明:
:滑动窗口的大小。
'sliding':滑动方式。@fun:要应用的函数。parameters:传递给函数的参数。
-
工作流程:
- 函数
fun将作用于矩阵 的每一列,输出为一个行向量。
- 滤波结果
的第
个元素是
的第
列应用
fun操作的结果。
- 函数
13、非线性空间滤波去噪(去除椒盐噪声)
(1)非线性空间滤波工具 ordfilt2
- 功能:
ordfilt2是用于生成顺序统计(或称为秩)滤波器的函数。- 它通过对邻域中的像素值进行排序,提取指定次序(秩)上的像素值,构成输出图像。
- 语法:
g = ordfilt2(f, order, domain)f:输入图像。order:提取排序后的第order个元素。domain:定义邻域范围。
- 例如:
- 最小值滤波器(Min Filter):
ordfilt2(f, 1, ones(m, n))。 - 中值滤波器:
ordfilt2(f, median(1:m*n), ones(m, n))。
- 最小值滤波器(Min Filter):
- 应用:
- 这类滤波器主要用于消除特定噪声,例如椒盐噪声。
(2)中值滤波器 medfilt2
- 功能:
- 中值滤波器是一种特殊的秩滤波器,是非线性空间滤波中最重要的工具之一。
- 它通过计算邻域内像素值的中值替换中心像素,达到平滑图像的目的。
- 语法:
g = medfilt2(f, [m n], padopt)m, n:邻域窗口大小。padopt:边界填充选项(如zeros、symmetric、indexed)。
- 默认边界处理为
zeros填充。
- 实验证明:
- 中值滤波对椒盐噪声有显著的去噪效果,同时保留边缘细节。
(3)中值滤波的去噪效果对比
- 原理与操作:
- 首先加载一幅受椒盐噪声污染的电路板图像(左图)。
- 对其进行不同模式的中值滤波处理:
- 默认
zeros填充方式(中图)。 symmetric填充方式(右图)。
- 默认



- 结果分析:
- 噪声图像(左图)经过中值滤波处理后:
- 使用默认边界模式(中图):边界处可能存在异常伪影。
- 使用
symmetric填充(右图):边界伪影显著减少,处理效果更平滑。
- 结果证明:
- 中值滤波对于椒盐噪声有显著的去除效果,尤其在
symmetric模式下表现更优。
- 中值滤波对于椒盐噪声有显著的去除效果,尤其在
- 噪声图像(左图)经过中值滤波处理后:
相关文章:

【图像处理lec3、4】空间域的图像增强
目录 1. 空间域图像增强的背景与目标 2. 空间域处理的数学描述 3. 灰度级变换 4. 幂律变换(Power-Law Transformation) 5、 分段线性变换 Case 1: 对比度拉伸 Case 2: 灰度切片 Case 3: 按位切片 6、对数变换(Logarithmic Transform…...

【算法day13】二叉树:递归与回溯
题目引用 找树左下角的值路径总和从中序与后序遍历构造二叉树 今天就简简单单三道题吧~ 1. 找到树左下角的值 给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。 假设二叉树中至少有一个节点。 示例 1: 输入: root [2,1,3] 输出: 1 我们…...

上海亚商投顾:创业板指缩量下跌 多只高位股午后跌停
上海亚商投顾前言:无惧大盘涨跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 一.市场情绪 市场全天震荡调整,创业板指领跌,高位股开始出现退潮,建设工业、星光股份、…...

单步调试Android Framework——App冷启动
纸上得来终觉浅,绝知此事要躬行。 —— [宋]陆游 基于aosp_cf_x86_64_phone-trunk_staging-eng , 下面是具体断点位置。 第一部分,桌面launcher进程 com.android.launcher3.touch.ItemClickHandler onClickonClickAppShortcutstartAppShor…...

统计一个目录下的文件及目录数量-linux010
要统计一个目录下的文件数量(包括子目录中的文件),可以使用以下命令: 1. 统计所有文件数量(包括子目录) 在终端中运行以下命令: find /path/to/directory -type f | wc -l 解释:…...

spring RestTemplate使用说明
rest-template是spring对httpclient的逻辑封装,它底层还是基于httpclient,所以一些配置其实跟httpclient是强相关的。 基本配置 rest-template可以不带参数,使用默认配置,也可以指定ClientHttpRequestFactory参数,Cl…...

thinkphp:try-catch捕获异常
使用简单的例子,实现了一个简单的try-catch捕获异常的实例 //开始事务Db::startTrans(); try{ //有异常抛出异常 if(存在错误){ throw new \Exception("异常信息"); } // 提交事务 Db::commit(); // 返回成功信息 ... } catch (\…...

shardingsphere分库分表跨库访问 添加分片规则
shardingsphere分库分表跨库访问 添加分片规则 建立 JDBC 环境 创建表 t_order: CREATE TABLE t_order (tid bigint(20) NOT NULL,tname varchar(255) DEFAULT NULL,goods_id bigint(20) DEFAULT NULL,tstatus varchar(255) DEFAULT NULL,PRIMARY KEY (tid) ) E…...

c++:std::map下标运算符的不合理使用
这是我分析之前遗留代码时发现的一个隐藏点;不过我并不认为这样使用std::map是合理的。 看看简化后的代码,v1、v2的值应该是多少呢? #include <map>std::map<int, int> cm[2];int get_cm_value(int device, int ctrl) { auto …...

KeyFormer:使用注意力分数压缩KV缓存
Keyformer: KV Cache Reduction through Key Tokens Selection for Efficient Generative Inference 202403,发表在Mlsys Introduction 优化KV cache的策略,主要是集中在系统级别的优化上,比如FlashAttention、PagedAttention,它…...
)
MetaGPT源码 (ContextMixin 类)
目录 理解 ContextMixin什么是 ContextMixin?主要组件实现细节 测试 ContextMixin示例:ModelX1. 配置优先级2. 多继承3. 多继承重写4. 配置优先级 在本文中,我们将探索 ContextMixin 类,它在多重继承场景中的集成及其在 Python 配…...
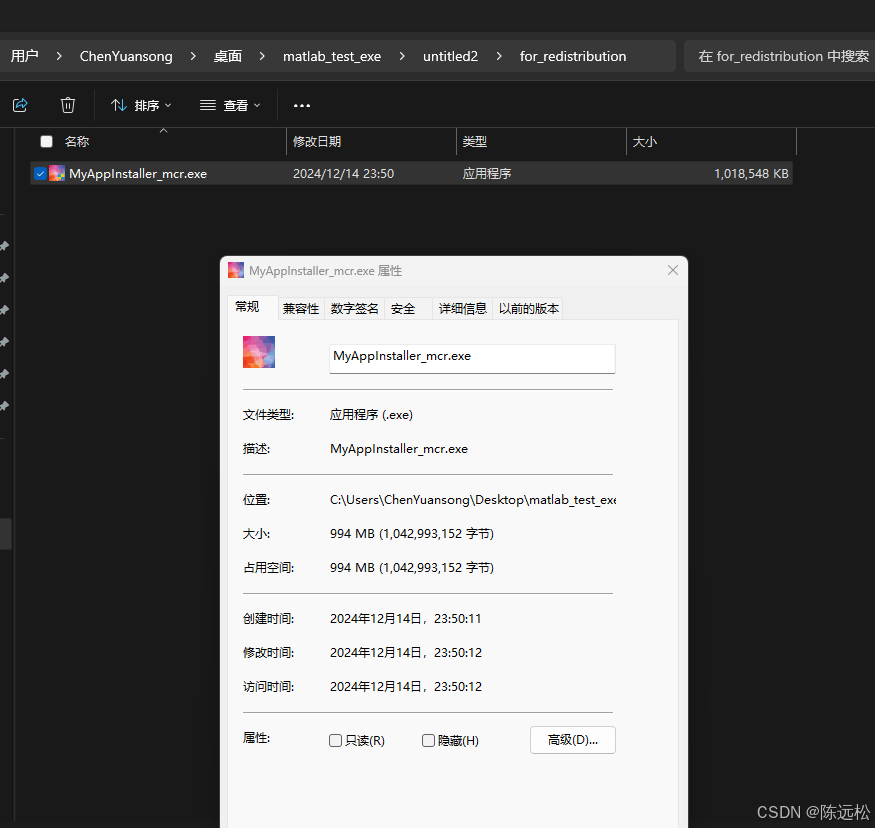
MATLAB生成.exe独立程序过程(常见问题解决方法)(2024.12.14)
本文只记录我执行过程中遇到的关键问题、以及解决方法,不讲诉整个流程。 电脑环境 win11系统 matlab 2024b 版本 整体流程 1.下载matlab运行时库,简写为MCR 2.配置MCR环境 3.打包程序 4.目标机器安装程序 一、下载MCR 下载这个折腾了大半天,大概问题就是…...

PHP排序算法:数组内有A~E,A移到C或者C移到B后排序,还按原顺序排序,循环
效果 PHP代码 public function demo($params){function moveNext($arr){$length count($arr);$lastElement $arr[$length - 1];for ($i $length - 1; $i > 0; $i--) {$arr[$i] $arr[$i - 1];}$arr[0] $lastElement;return $arr;}function moveAndReplace($array, $from…...
ChatGPT搜索全新升级,向全体用户开放,近屿智能助力AI行业发展
12月17日,OpenAI在第八天直播中正式宣布ChatGPT搜索功能全面升级,并即日起对所有ChatGPT用户开放。此次更新不仅带来了显著的性能提升,还引入了多项突破性功能,如更快的搜索速度、全新的地图体验以及YouTube视频嵌入,为…...

win10配置免密ssh登录远程的ubuntu
为了在终端ssh远程和使用VScode远程我的VM上的ubuntu不需要设置密码,需要在win10配置免密ssh登录远程的ubuntu。 在win10打开cmd,执行下面的代码生成密钥对(会提示进行设置,按照默认的配置就行,一直回车)&…...

skywalking 搭建 备忘录
基础环境 apache-skywalking-apm-9.6.0.tar.gz apache-skywalking-java-agent-9.1.0.tgz elasticsearch 7.14.1 采用dockers搭建 或者手动部署 kibana 可视化 应用 微服务版 consumer.jar eureka.jar 注册中心 provider.jar skywalking 地址 https://skywalkin…...
)
linux日常常用命令(AI向)
进程挂后台运行 nohup sh ./scripts/*****.sh > ./output/*****.log 2>&1 &删除***用户的所有python进程 pkill -u *** -f "^python"列出“***”用户的进程信息 ps aux --sort-%mem | grep ^***git add ./*git commit -m "注释"git push …...

信奥赛CSP-J复赛集训(bfs专题)(5):洛谷P3395:路障
信奥赛CSP-J复赛集训(bfs专题-刷题题单及题解)(5):洛谷P3395:路障 题目描述 B 君站在一个 n n n\times n n...

《红队和蓝队在网络安全中的定义与分工》
网络安全中什么是红队蓝队 在网络安全领域,红队和蓝队是一种对抗性的演练机制,用于测试和提升网络安全防御能力。 红队(Red Team) 定义与目标 红队是扮演攻击者角色的团队。他们的主要任务是模拟真实的网络攻击,利用各…...
李宏毅深度强化学习入门笔记:PPO
李宏毅-深度强化学习-入门笔记:PPO 一、Policy Gradient(一)基本元素(二)Policy of Actor1. Policy π \pi π 是带有参数 θ \theta θ 的 network2. 例子:运行流程 (三)Actor, E…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
