python模拟练习第一期
问题一
如果一个数 p 是个质数,同时又是整数 a的约数,则 p 称为 a的一个质因数。
请问 2024 有多少个质因数?
步骤 1: 分解 2024
首先,2024 是偶数,说明可以被 2 整除。我们从 2 开始进行除法分解:
2024÷2=1012
1012÷2=506
506÷2=253
253 不是偶数,所以它不能再被 2 整除。我们接下来检查 253 能否被 3 整除。因为 253 各位数字之和 2+5+3=10,10 不能被 3 整除,因此 253 不能被 3 整除。
接下来检查 253 能否被 5 整除,253 末尾不是 0 或 5,所以不能被 5 整除。
然后检查 253 能否被 11 整除。计算 253 除以 11:
253÷11=23
所以,253 可以被 11 整除,商为 23。23 是一个质数,无法再分解。
步骤 2: 质因数分解
通过以上步骤,我们可以得出 2024 的质因数分解:
2024=23×11×232024=23×11×23
步骤 3: 质因数的个数
质因数包括 2、11 和 23。因此,2024 的质因数有 3 个,分别是 2、11 和 23。
答案:
2024 的质因数有 3 个。
问题二
对于一个整数 n ,我们定义一次开根变换会将 n 变为开根号后的整数部分。即变为平方和不超过 n 的数中的最大数。
例如,20 经过开根变换将变为 4 ,如果再经过一次开根变换将变为 2 ,如果再经过一次开根变换将变为 1 。
请问,2024经过多少次开根变换后会变为 1 ?
初始值为 2024。
第一次开根变换:2024≈45.0112024≈45.011,取整数部分为 45。
第二次开根变换:45≈6.70845≈6.708,取整数部分为 6。
第三次开根变换:6≈2.4496≈2.449,取整数部分为 2。
第四次开根变换:2≈1.4142≈1.414,取整数部分为 1。
因此,2024经过 4 次开根变换后会变为 1。
代码计算:
import math
def abc(n):c = 0while n > 1:n = math.isqrt(n) c += 1return c
n = 2024
a = abc(n)
print(a)问题三
小蓝有很多 1x1x1 的小立方体,他可以使用多个立方体拼成更大的立方体。
例如,小蓝可以使用 8 个小立方体拼成一个大立方体,每边都是 2 个。
又如,小蓝可以使用 27 个小立方体拼成一个大立方体,每边都是 3 个。
现在,小蓝有 2024 个小立方体,他想再购买一些小立方体,用于拼一个超大的立方体,要求所有的小立方体都用上,拼成的大立方体每边长度都相等。 请问,小蓝最少需要购买多少个小立方体?
大立方体的体积: 一个边长为 n 的大立方体的体积是 n**3(即 n×n×n)。
目标: 我们需要找到一个 n,使得 n**3≥2024,并且 n**3−2024 是最小的,即最少需要购买的立方体数量。
计算 2024 的立方根,以估计一个接近的 nn。我们可以用计算器计算:
2024≈12.6348
因此,边长 n 至少应该是 13,因为 123=1728小于 2024,而 133=2197 大于 2024。
133=2197 是一个大立方体的体积。
小蓝已经有 2024 个小立方体,所以他需要购买的数量是:
2197−2024=173
代码计算:
n = 2024
i = 13
while i**3 < n:i += 1
x = i**3
a = x - n
print("小蓝最少需要购买的立方体数量:", a)问题四
如果一个日期的日期以 1 结尾(1日、11日、21日、31日)且为星期一,则称这个日期为一好日期。
请问从 1901 年 1 月 1 日至 2024 年 12 月 31 日总共有多少个一好日期。
提示:1901 年 1 月 1 日是星期二。
确定日期范围: 从 1901 年 1 月 1 日到 2024 年 12 月 31 日。
了解每个月的 "1 日"、"11 日"、"21 日"、"31 日": 这些是以 1 结尾的日期。我们需要检查每个月这些日期是否是星期一。
确定每年的每个月的具体情况: 每年的不同月份中,某些月份的日期可能会出现 31 日,而有些月份(如 2 月、4 月、6 月等)没有 31 日。
确定每个日期是星期几: 利用已知的起始日期(1901 年 1 月 1 日是星期二),我们可以通过计算每个日期的星期几来确定是否是星期一。
代码计算:
import datetime
start_date = datetime.date(1901, 1, 1)
good_dates_count = 0# 遍历从1901年1月1日到2024年12月31日的日期
for year in range(1901, 2025):for month in range(1, 13):# 检查该月的1日、11日、21日、31日(如果有31日)for day in [1, 11, 21]:try:# 创建该日期current_date = datetime.date(year, month, day)# 如果该日期是星期一(星期一对应的数字是0)if current_date.weekday() == 0:good_dates_count += 1except ValueError:# 如果日期无效(如2月30日),则跳过pass# 检查31日是否在该月中有效if month in [1, 3, 5, 7, 8, 10, 12]: # 有31日的月份try:current_date = datetime.date(year, month, 31)if current_date.weekday() == 0:good_dates_count += 1except ValueError:pass
print("一好日期的总数是:", good_dates_count)
问题五
两个数按位异或是指将这两个数转换成二进制后,最低位与最低位异或作为结果的最低位,次低位与次低位异或作为结果的次低位,以此类推。
例如,3 与 5 按位异或值为 6 。
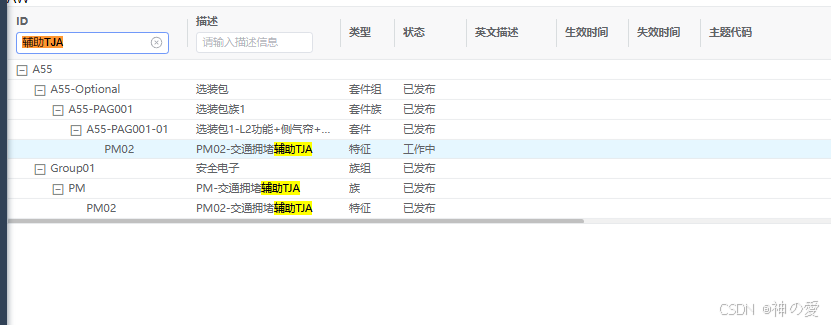
小蓝有以下 30 个整数:
9226, 4690, 4873, 1285, 4624, 1596, 6982, 590, 8806, 121, 8399, 8526, 5426, 64, 9655, 7705, 3929, 3588, 7397, 8020, 1311, 5676, 3469, 2325, 1226, 8203, 9524, 3648, 5278, 8647.
小蓝想找一个整数 V ,使得 V 与这 30 个数分别异或后,得到的 30 个数的平方和最小。请问平方和最小是多少?
1.将每个数转换为 16 位二进制数(因为最大数 9655 的二进制表示需要 14 位,可以补充到 16 位来统一处理)。
2.对每一位,统计 30 个数中该位为 1 的数量。
3.如果该位为 1 的数量超过一半(即大多数数在该位上是 1),则选择 V在这一位上为 1,否则为 0。
4.根据得到的 V 计算每个 ai⊕V 的平方和。
代码计算:
nums = [9226, 4690, 4873, 1285, 4624, 1596, 6982, 590, 8806, 121, 8399, 8526, 5426,64, 9655, 7705, 3929, 3588, 7397, 8020, 1311, 5676, 3469, 2325, 1226, 8203,9524, 3648, 5278, 8647
]
bit_length = 16
count_ones = [0] * bit_length
for num in nums:for i in range(bit_length):if num & (1 << (bit_length - 1 - i)):count_ones[i] += 1
V = 0
for i in range(bit_length):if count_ones[i] > len(nums) // 2:V |= (1 << (bit_length - 1 - i))
squared_sum = 0
for num in nums:squared_sum += (num ^ V) ** 2
print(f"最小的平方和是: {squared_sum}")
问题六
小蓝在一个停车场停车。
停车场的收费规则为:每 15 分钟收费 2 元,不满 15 分钟的不收费。
小蓝总共停车 n 分钟,请问收费总额是多少?
【输入格式】 输入一行包含一个整数 n ,表示小蓝停车的时长。
【输出格式】 输出一行包含一个整数,表示停车费用。
【样例输入】 150
【样例输出】 20
【样例输入】 2024
【样例输出】 268
我们可以使用整数除法和取余操作来帮助我们确定停车时长的分段数。
可以用 (n + 14) // 15 来计算向上取整的次数。如果 n 不是15的整数倍,就多计一段。
例如:对于 n = 16,(16 + 14) // 15 的结果是 2,表示收费2段15分钟。
每段15分钟收费2元,所以最终收费就是 (n + 14) // 15 * 2。
代码计算
n=int(input())
if(n>=15):b=n//15c=b*2
print(c)问题七
小蓝有一个整数 n ,每次操作,可以将这个整数的每个非零数位减少 1 。
请问经过多少次操作,这个数会变为 0 。
例如,整数 2024 经过一次操作变为 1013,再经过一次操作变为 2 (即0002),再经过两次操作变为 0 ,总共经过 4 次变换变为 0 。
【输入格式】 输入一行包含一个整数 n 。
【输出格式】 输出一行,包含一个整数,表示答案。
【样例输入】 2024
【样例输出】 4
观察每一位:整数的每一位非零数字在每一次操作中都会减少 1,直到该位数字变成 0。
操作次数:可以通过统计该整数各位的最大值来判断操作次数。因为每一位数字都会在每一次操作中减少 1,所以最终需要进行的操作次数就是这整个数各位最大数字的数量。
代码计算:
def min_operations_to_zero(n):# 转换为字符串,遍历每一位字符digits = str(n)# 找出所有非零数字的最大值max_digit = max(int(d) for d in digits if d != '0')return max_digitn = int(input().strip())print(min_operations_to_zero(n))
问题八
小蓝有一个减法式子,形如 a-b,其中 a 和 b 都是非负整数(不保证结果非负)。
请编程处理这个式子,输出运算结果。
【输入格式】 输入一行包含一个减法表达式,式子中仅含数字字符和一个减号。
【输出格式】 输出一行包含一个整数,表示运算结果。
【样例输入】 2024-1949
【样例输出】 75
【样例输入】 20-24
【样例输出】 -4
输入格式中有一个减法符号 -,它将两个数字 a 和 b 分开。我们可以利用这个符号来分割输入字符串,从而得到 a 和 b。
将解析出来的 a 和 b 转换为整数后,直接进行减法运算,得出结果。
代码计算:
e = input().strip()
a, b = e.split('-')
a = int(a)
b = int(b)
print(a - b)
问题九
小蓝有一个长度为 n 的整数数列 a[1], a[2], ..., a[n] 。
对于一个给点的整数 k ,小蓝想找到相邻间隔为 1 的 k 个数 a[p], a[p+2], a[p+4], ..., a[p+2k-2],使得他们的和最大。其中 1 <= p <= n-2k+2。
给定数列和 k ,请问给出最大的和。
【输入格式】 输入的第一行包含一个整数 n 。
第二行包含 n 个整数,相邻数之间使用一个空格分隔,依次表示 a[1], a[2], ..., a[n] 。
第三行包含一个整数 k 。
【输出格式】 输出一行,包含一个整数,表示答案。
【样例输入】 10 2 1 4 7 4 8 3 6 4 7 2 【样例输出】 15 【样例说明】 取 p=4,a[4]+a[6]=7+8=15 最大。
代码计算:
def max_sum(n, a, k):max_sum_value = float('-inf')for p in range(n - 2 * k + 2):current_sum = 0for i in range(k):current_sum += a[p + 2 * i] # a[p], a[p+2], ..., a[p+2k-2]max_sum_value = max(max_sum_value, current_sum)return max_sum_value
n = int(input())
a = list(map(int, input().split()))
k = int(input())
result = max_sum(n, a, k)
print(result)
问题十
小蓝有一个长度为 n 的整数序列 a[1], a[2], ..., a[n] 。
他希望从中找出一个最长的子序列,形成一个勾的形状(√)。
即找到 1 <= p[1] < p[2] < ... < p[k] <= n,满足 a[p[1]] > a[p[2]] > a[p[3]] > ... > a[p[x]] < a[p[x+1]] < ... < a[p[k]] 。其中 k 是子序列的长度,x 是勾中最小的位置。目标是使得 k 最大。
请找出最大的勾的长度。
【输入格式】 输入的第一行包含一个整数 n 。
第二行包含 n 个整数,相邻数之间使用一个空格分隔,依次表示 a[1], a[2], ..., a[n] 。
【输出格式】 输出一行,包含一个整数,表示答案。
【样例输入】 10 2 1 4 7 4 8 3 6 4 7 【样例输出】 5 【样例说明】 当 p = (4,5,7,9,10) 时,a[4] , a[5] , a[7] , a[9] , a[10] 可形成一个长度为 5 的勾:7,4,3,6,7。
代码计算:
def longest_hoop(n, a):dec = [1] * ninc = [1] * nfor i in range(1, n):for j in range(i):if a[i] < a[j]:dec[i] = max(dec[i], dec[j] + 1)for i in range(n - 2, -1, -1):for j in range(n - 1, i, -1):if a[i] < a[j]:inc[i] = max(inc[i], inc[j] + 1)# 计算勾的最大长度max_length = 0for i in range(n):if dec[i] > 1 and inc[i] > 1:max_length = max(max_length, dec[i] + inc[i] - 1)return max_lengthn = int(input())
a = list(map(int, input().split()))
print(longest_hoop(n, a))
相关文章:

python模拟练习第一期
问题一 如果一个数 p 是个质数,同时又是整数 a的约数,则 p 称为 a的一个质因数。 请问 2024 有多少个质因数? 步骤 1: 分解 2024 首先,2024 是偶数,说明可以被 2 整除。我们从 2 开始进行除法分解: 202…...
Xcode
info.plist Appearance Light 关闭黑暗模式 Bundle display name 设置app名称,默认为工程名 Location When In Use Usage Description 定位权限一共有3个key 1.Privacy - Location When In Use Usage Description 2.Privacy - Location Always and When In U…...
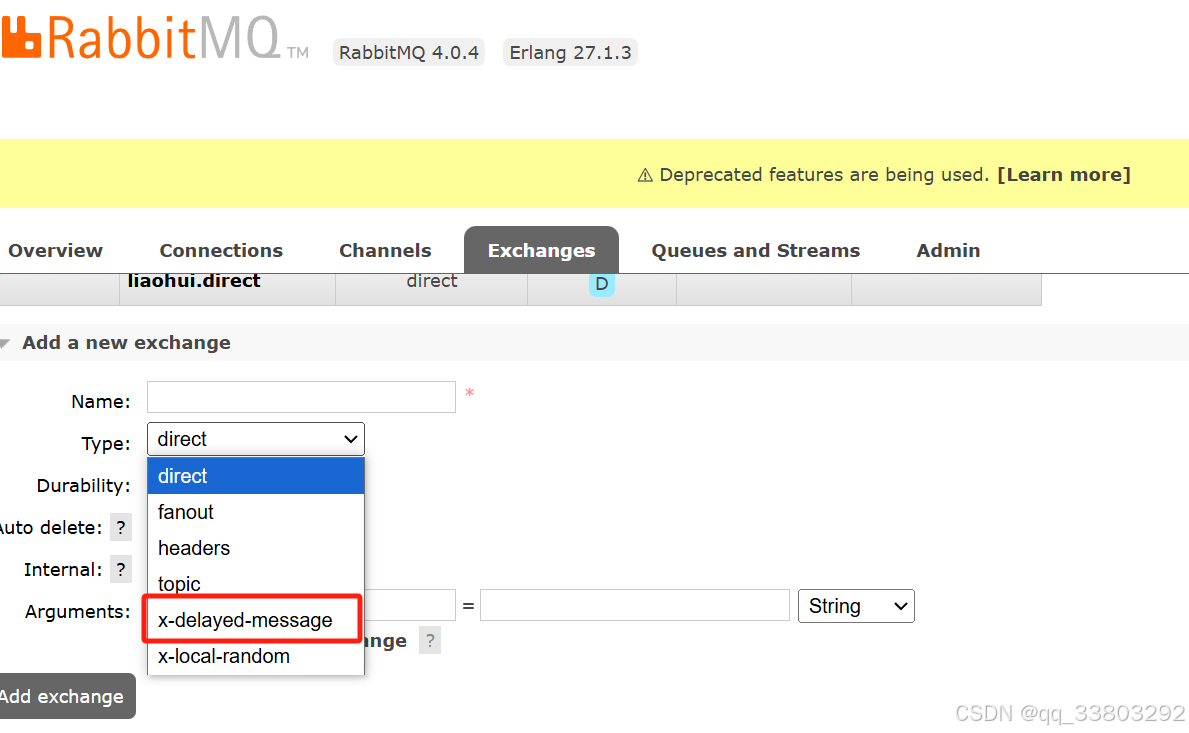
RabbitMQ安装延迟消息插件(mq报错)
之前启动一个springboot的单体项目,一直mq的错误,即便我更新了最新版本的mq,还是报错。 后来才发现,项目使用了延时队列,是需要单独下载延时插件的。 1如果判断mq有没有延时队列插件【没有x-delayed-message】 2下载…...

es 3期 第15节-词项查询与跨度查询实战运用
#### 1.Elasticsearch是数据库,不是普通的Java应用程序,传统数据库需要的硬件资源同样需要,提升性能最有效的就是升级硬件。 #### 2.Elasticsearch是文档型数据库,不是关系型数据库,不具备严格的ACID事务特性ÿ…...

iOS Delegate模式
文章目录 一、 Delegate 模式的概念二、Delegate 的实现步骤步骤 1: 定义一个协议(Protocol)步骤 2: 在主类中添加一个 delegate 属性步骤 3: 实现协议的类遵守协议并实现方法步骤 4: 设置 delegate 三、Delegate 模式的特点四、Delegate 模式的常见场景…...

java-使用druid sqlparser将SQL DDL脚本转化为自定义的java对象
java-使用druid sqlparser将SQL DDL脚本转化为自定义的java对象 一、引言二、环境三、待解析的DDL四、解析后的对象结构五、完整的UT类六、控制台输出总结 一、引言 在日常开发中,有些需要对SQL进行解析的场景,比如读取表结构信息,生成文档、…...
)
React状态管理常见面试题目(一)
1. Redux 如何实现多个组件之间的通信?多个组件使用相同状态时如何进行管理? Redux 实现组件通信 Redux 是一个集中式的状态管理工具,通过共享一个全局 store 来实现多个组件之间的通信。 通信机制: 所有状态保存在 Redux 的全局 store 中。使用 ma…...
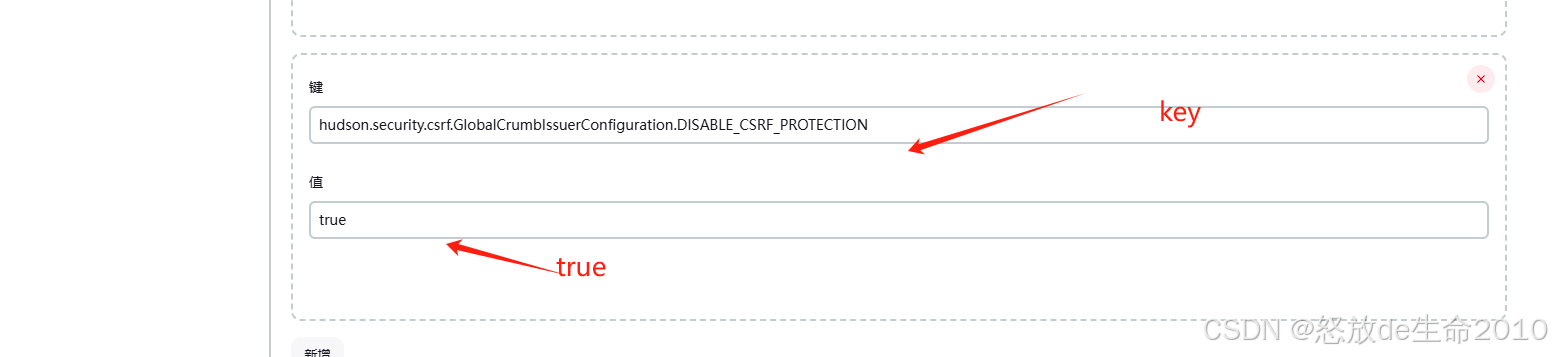
jenkins 出现 Jenkins: 403 No valid crumb was included in the request
文章目录 前言解决方式:1.跨站请求为找保护勾选"代理兼容"2.全局变量或者节点上添加环境变量3.(可选)下载插件 the strict Crumb Issuer plugin4.重启 前言 jenkins运行时间长了,经常出现点了好几次才能构建,然后报了Je…...

【前端面试】list转树、拍平, 指标,
这个题目涉及的是将一组具有父子关系的扁平数据转换为树形结构,通常称为“树形结构的构建”问题。类似的题目包括: 1. 组织架构转换 给定一个公司的员工列表,每个员工有 id 和 managerId,其中 managerId 表示该员工的上级。任务…...

游戏引擎学习第43天
仓库 https://gitee.com/mrxiao_com/2d_game 介绍运动方程 今天我们将更进一步,探索运动方程,了解真实世界中的物理,并调整它们,以创建一种让玩家感觉愉悦的控制体验。这并不是在做一个完美的物理模拟,而是找到最有趣…...

NVM:安装配置使用(详细教程)
文章目录 一、简介二、安装 nvm三、配置 nvm 镜像四、配置环境变量五、使用教程5.1 常用命令5.2 具体案例 六、结语 一、简介 在实际的开发和学习中可能会遇到不同项目的 node 版本不同,而出现的兼容性问题。 而 nvm 就可以很好的解决这个问题,它可以在…...
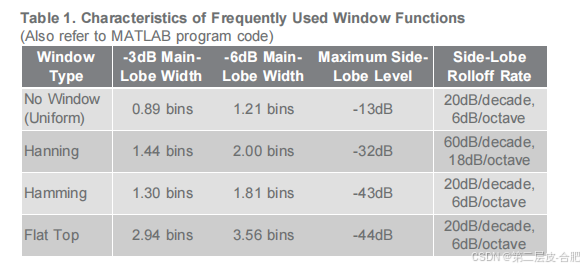
matlab测试ADC动态性能的原理
目录 摘要: 简介: 动态规范和定义 动态规格: 双面到单边的功率谱转换 摘要: 模数转换器(adc)代表了接收器、测试设备和其他电子设备中的模拟世界和数字世界之间的联系。正如本文系列的第1部分中所概述…...

PostgreSQL JSON/JSONB 查询与操作指南
PostgreSQL 提供了强大的 JSON 和 JSONB 数据类型及相关操作,适用于存储和查询半结构化数据。本文将详细介绍其常用操作。 1. 基础操作 1.1 JSON 属性访问 ->: 返回 JSON 对象中的值,结果为 JSON 格式。 SELECT {"a": {"b": 1…...
【Isaac Lab】Ubuntu22.04安装英伟达驱动
目录 1.1 禁用nouveau驱动 1.2 安装必要的依赖项 1.3 下载安装 1.4 查看是否安装成功 1.5 安装CUDA 1.5.1 下载 1.5.2 按照提示进行下载安装 1.5.3 添加环境变量 1.5.4 测试CUDA是否安装成功 1.1 禁用nouveau驱动 输入以下命令打开blacklist.conf文件 sudo vim /etc…...
JS,递归,处理树形数据组件,模糊查询树形结构数据字段
JS递归如何模糊查询树形结构数据,根据数据中的某一个字段值,模糊匹配 直接拿去使用就行 function filterTreeLabel(arr, label) {let result []arr.forEach((item) > {// if (String(item.POBJECT_NAME).toLowerCase().indexOf(label)!-1) {if (String(item.P…...

神州数码DCME-320 online_list.php 任意文件读取漏洞复现
0x01 产品描述: 神州数码DCME-320是一款高性能多业务路由器,专为多用户、多流量和多业务种类需求设计。它采用了...

nginx的内置变量以及nginx的代理
nginx的内置变量 客户端 命令含义$uri可以获取客户端请求的地址,包含主机和查询的参数$request_uri:获取客户端的请求地址,包含主机和查询参数。$host:请求的主机名,客户端—发送请求的url地址$http_user_agent获取客户端请求的浏览器和操作…...
ubuntu监测硬盘状态
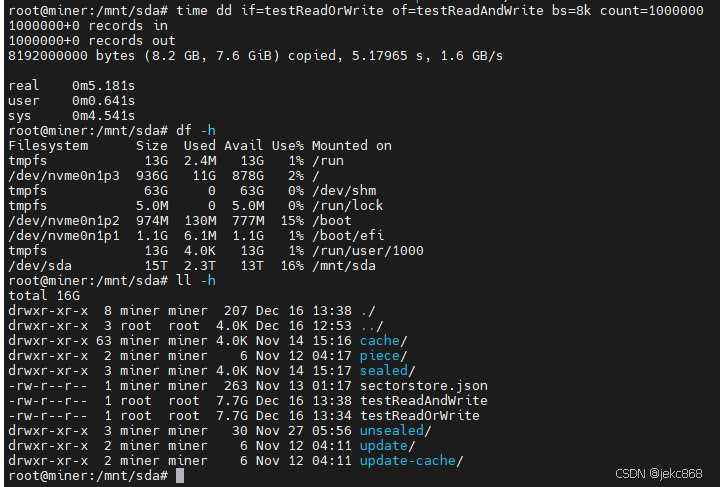
安装smartmontools smartctl -l error /dev/sdk smartctl -i /dev/sda lshw -class disk smartctl -H /dev/sd 结果1: 结果2:PASSED,这表示硬盘健康状态良好 smartctl -a /dev/sdb sdk lsblk blkid 测试写入速度 time dd if/dev/zero of…...

3.2.1.2 汇编版 原子操作 CAS
基本原理说明 在 x86 和 ARM 架构上,原子操作通常利用硬件提供的原子指令来实现,比如 LOCK 前缀(x86)或 LDREX/STREX(ARM)。以下是一些关键的原子操作(例如原子递增和比较交换)的汇…...

InnoDB事务系统(二):事务的实现
事务隔离性由锁来实现。原子性、一致性、持久性通过数据库的 redo log 和 undo log 来完成。 redo log 称为重做日志,用来保证事务的原子性和持久性。undo log 用来保证事务的一致性。 有的 DBA 或许会认为 undo 是 redo 的逆过程,其实不然。redo 和 u…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...
