【博弈模型】古诺模型、stackelberg博弈模型、伯特兰德模型、价格领导模型
博弈模型
- 1、古诺模型(cournot)
- (1)假设
- (2)行为分析
- (3)经济后果
- (4)例题
- 2、stackelberg博弈模型(产量领导模型)
- (1)基本假设
- (2)行为分析
- 第一步:求追随者反应函数。
- 第二步:求领导者利润最大化的条件
- 第三步:求追随者利润最大化
- (4)例题
- 3、伯特兰德模型
- (1)假设
- (2)行为分析
- (3)均衡
- (4)缺陷(不现实性)
- 4、价格领导模型
- (1)假设
- (2)行为分析
- (3)例题
1、古诺模型(cournot)
(1)假设
-
假设一:是双寡头市场、厂商的成本函数相同为C(Q)。
-
假设二:产品同质(产品包装、质量、售前售后等完全相同)。对于消费者而言,厂商的产品是完全替代品。
-
假设三:决策变量为产量,并且同时行动。因此只能预测对方的产量(一定要预测),相当于是静态的博弈。
假设市场的需求曲线为:
-
假设四:认为对方不会对自己的行为作出一系列的反应。(因为是同时行动的)
用式子表达为:
(2)行为分析
A厂商决定产量的时候,会预测B厂商,但A认为B不会对自己的预测行为作出任何反应。
寡头厂商1在预测厂商2的产量的基础上,以利润最大化目标决定自身产量。
寡头厂商2在预测厂商1的产量的基础上,以利润最大化目标决定自身产量。

厂商1:

最大化利润即使一阶导数为0。


(3)经济后果
-
总产量如何?
行业产量=市场总量×(m/m+1)
其中,m为厂商个数 -
单个厂商的产量如何?
单个厂商=市场总量×(1/m+1) -
均衡是否稳定?
稳定。在实现古诺均衡的时候,每个厂商都在预测对方产量的基础上决定自己的产量的时候达到了自身利润的最大化。没有离开这个均衡状态的动机,也就是每个人都不会愿意去改变自己的产量。
(4)例题
双寡头市场当中,两厂商进行产量竞争,他们面临的总市场需求曲线为P=100-Q,两厂商的生产成本相同,皆为C=4Q。问:若进行古诺竞争,求市场均衡价格和两厂商的产量,以及各自的利润是多少(暗含条件:利润最大化)。
解:

因为是古诺竞争,所以厂商1的利润函数为π1=P×Q1-C(Q1)=销售量-总成本。
因为P=100-Q,所以P=100-(Q1+Q2),所以π1=[100-(Q1+Q2)]×Q1-4Q1
所以对π1求关于Q1的一阶导得Q1=f(Q2)


2、stackelberg博弈模型(产量领导模型)
(1)基本假设
- 假设一:行动有先后,领导者先行,追随者后行。
- 假设二:核心领导变量为产量
- 假设三:领导者的产量决策起支配作用,并且他的决策会充分估计追随者的反应。
因此首先应该分析追随者的反应函数,再分析领导者行为。
(2)行为分析
第一步:求追随者反应函数。
- 追随者利润最大化的函数 max π2 =P×Q2-C(Q2)

- 对Q2求偏导

- 得到厂商2(追随者)的反应函数

厂商1(领导者)是没有反应函数的,因为其是先做决策。
第二步:求领导者利润最大化的条件
领导者做决定的最主要的因素应该是厂商2的反应。也就是反应函数求出来是为了帮助领导者做决策。

因此可以直接把这个条件代入π1。

第三步:求追随者利润最大化

(4)例题
假设两个厂商分别为厂商1和厂商2,假定他们遵循的是stackelberg的竞争方式。他们面临共同的市场需求函数为P=100-Q。厂商1的成本函数为C1=10Q1,厂商2的成本函数为C2=Q2^2。
假设厂商1为领导者,厂商2为追随者,求市场的均衡价格以及各自的均衡产量、利润。




一般来说,领导者得到的利润会大于追随者,也就是“先发优势、先动优势”。
3、伯特兰德模型
(1)假设
假设一:假定只有两个寡头厂商,以价格作为决策变量,且产品完全同质。
假设二:面临的需求函数

假设三:假设生产成本相同且MC=AC=C(C为常数)
(2)行为分析
情况一:若P1>P2,厂商1的价格大于厂商2的价格,。因此厂商1会失去所有的市场,利润为0。
情况二:若P1=P2,则二者平分市场。
情况三:若P1<P2,此时厂商1 获得所有市场。



伯特兰德模型是以价格作为决策变量,因此最后的利润函数也是和价格有关的。
(3)均衡
P1=P2=AC=表示利润是0的情况。
P1=P2=MC=表示有效配置。

MC=AC=表示实现了最优的均衡配置。
此时达到稳定,如果有人提价,那么他将失去所有的市场;如果有人降价,他将亏损。
(4)缺陷(不现实性)
现实生活当中,有一些原因导致即使价格更高,也不会失去所有的市场,具体原因有:
1、产品存在差异
2、博弈的时序问题
3、生产约束问题
4、价格领导模型
stackelberg博弈模型和价格领导模型有一定的相似性。
- stackelberg博弈模型:是领导者先决定产量,追随者再根据既定的领导者决定的产量的基础上决定其利润最大化的行为。
- 价格领导模型:是领导者先决定价格,追随者在领导者既定的价格下再实现自己的利润最大化。
(1)假设
假设一:领导者决定的是价格P,则追随者将其视为既定的价格来接受。(追随者只能在领导者定下来的基础上来进行决策 )
假设二:领导者采取价格作为决策变量,追随者会对此有反应。
(2)行为分析


供给函数表达的是价格与产量之间的关系
(3)例题
设AB两厂商,A为领导者,B为追随者。


若A决定市场价格(价格领导),则:
(1)求A的产量为多少?
(2)求A的定价为多少?
(3)求B的产量为多少?
解:
第一步:求追随者的供给函数
在分析完全竞争市场,分析厂商行为的时候,我们知道,边际成本就是供给函数。(边际成本与可变成本的最低点的交点以上的边际成本的部分)


第二步:领导者依据追随者的供给函数探讨自己的产量为多少

第三步:求出最优的产量QA


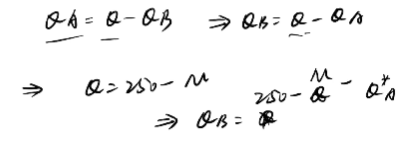
相关文章:
【博弈模型】古诺模型、stackelberg博弈模型、伯特兰德模型、价格领导模型
博弈模型 1、古诺模型(cournot)(1)假设(2)行为分析(3)经济后果(4)例题 2、stackelberg博弈模型(产量领导模型)(1ÿ…...
)
单片机:实现花样灯数码管的显示(附带源码)
单片机实现花样灯数码管显示 数码管(七段数码管)广泛用于数字显示,例如时钟、计数器、温度计等设备。在本项目中,我们将使用单片机实现花样灯数码管的显示效果。所谓花样灯显示是指通过控制数码管上的各个段位,以不同…...
什么是芯片电阻
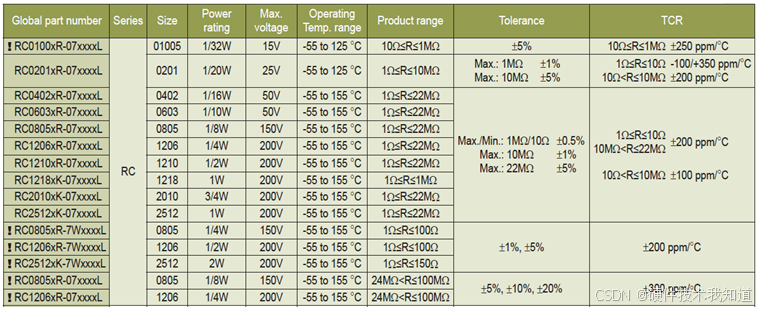
有人把Chip Resistor翻译成“芯片电阻”,我觉得翻译成“贴片电阻”或“片状电阻”更合适。有些厂商也称之为”电阻片”,英文写作Resistor Chip。比如:Thick film resistor chips(厚膜电阻片)、Thin film resistor chip…...
和(2D 直线\3D 平面)转换函数 (五))
【C++】sophus : geometry.hpp 位姿(SE2 和 SE3)和(2D 直线\3D 平面)转换函数 (五)
这段代码定义了一系列在位姿(SE2 和 SE3)和几何实体(2D 直线和 3D 平面)之间进行转换的函数。它利用了 Sophus 库中已有的旋转表示(SO2 和 SO3)。 以下是函数的详细解释: 1. SO2 与直线…...
获取时间)
moment()获取时间
moment 是一个 JavaScript 日期处理类库。 使用: //安装 moment npm install moment -- save引用 //在main.js中全局引入 import moment from "moment"设定moment区域为中国 //import 方式 import moment/locale/zh-cn moment.locale(zh-cn); 挂载全…...

Azure虚拟机非托管磁盘大小调整
想要扩容一个Azure VM 的磁盘空间,门户里面竟然无法扩展,点点鼠标就完事的时代在离去,微软越来不想微软。 在门户里面即便使用Azure Cli命令行也不行。 PS /home/gpchina> az disk list [] 返回为空,根本没有返回磁盘。 不过使…...

流匹配模型[Flow Matching]
流匹配模型:概念、优缺点与扩散模型的对比 在生成建模领域,流匹配模型(Flow Matching)是一种通过学习流场将初始分布(通常是高斯噪声)变换为目标分布的新型框架。本文将对流匹配模型的概念、与扩散模型的联…...

Unix 和 Windows 的有趣比较
Unix 和 Windows NT 比较 来源于这两本书,把两本书对照来读,发现很多有意思的地方: 《Unix 传奇》 https://book.douban.com/subject/35292726/ 《观止 微软创建NT和未来的夺命狂奔 》 Showstopper!: The Breakneck Race to Create Windows…...
——贪心算法)
算法(三)——贪心算法
文章目录 定义基本原理基本思路优缺点优点缺点 经典案例及解析找零问题问题描述贪心思路算法解析java代码示例 活动选择问题问题描述贪心思路算法解析java代码示例 车辆路径问题问题描述贪心思路算法分析java代码示例 定义 贪心算法是指在求解问题时,总是做出在当前…...

LeetCode 704.二分查找
LeetCode 704.二分查找 思路🧐: 在本篇以及之后几篇的博客中,博主将会用二分法进行解答,以此巩固二分题型。二分法一般用于具有二段性的数据中使用。比如该题为有序数组,需要我们查找一个目标值target,分析…...
Linux介绍与安装CentOS 7操作系统
什么是操作系统 操作系统,英⽂名称 Operating System,简称 OS,是计算机系统中必不 可少的基础系统软件,它是 应⽤程序运⾏以及⽤户操作必备的基础环境 ⽀撑,是计算机系统的核⼼。 操作系统的作⽤是管理和控制计算机系…...

使用 rbenv 切换 Ruby 版本
1. 查看当前 Ruby 版本 首先,查看当前系统中安装的 Ruby 版本: ruby -v如果你已经安装了 rbenv,可以列出通过 rbenv 安装的 Ruby 版本: rbenv versions2. 安装 Ruby 版本 如果你想安装新的 Ruby 版本,使用以下命令…...
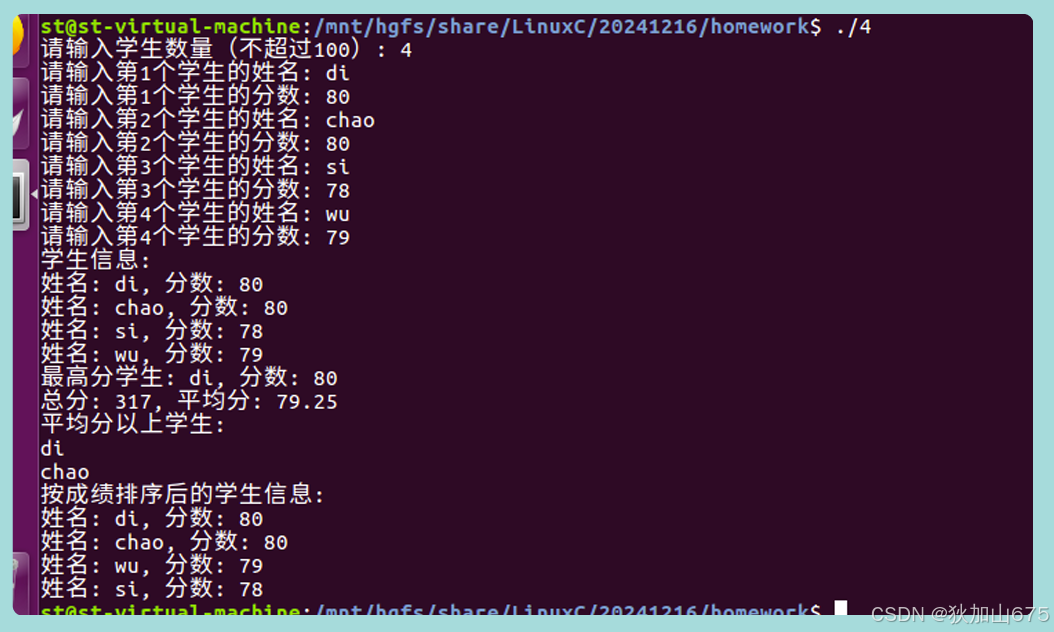
C语言(结构体练习)
设计一个结构体,存放一个学员信息并显示,存放两个学员信息,算他们的平均分。 #include <stdio.h> #include <string.h>// 定义结构体 typedef struct {char name[50];float score; } Student;// 函数声明 void display(Student student); f…...

你了解网络层的 ICMP 吗?
你了解网络层的 ICMP 吗? 一. 什么是 ICMP二. ICMP 的工作原理三. ICMP 的结构四. ICMP 的常见应用五. ICMP 的局限性与安全性六. 总结 前言 这是我在这个网站整理的笔记,有错误的地方请指出,关注我,接下来还会持续更新。 作者:神…...
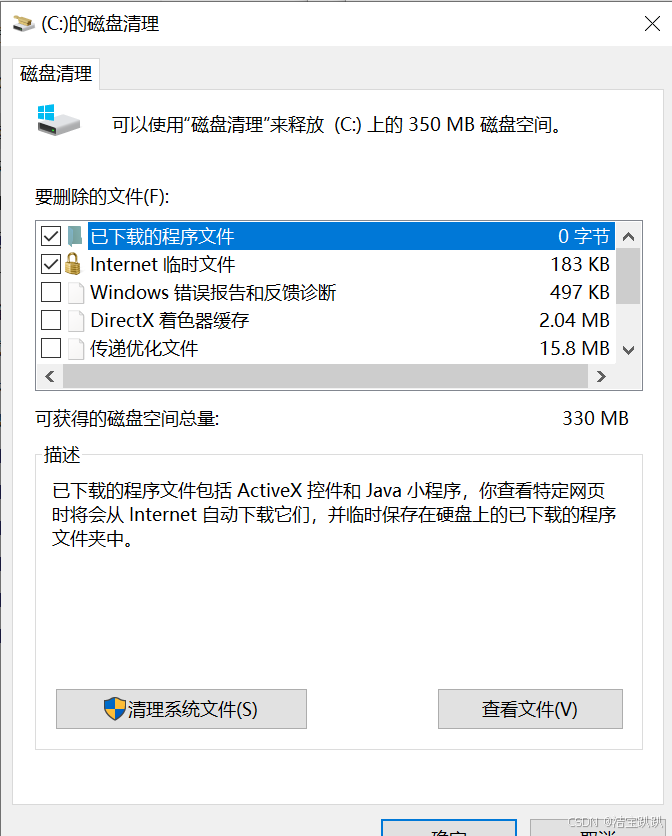
清理C盘小记
突然C盘就爆满了,想当初还是给他预留了120G的空间,感觉到现在也不够用了,担心出现死机的情况就赶紧进行了清理。有一说一,清理回收站是真的有用。 参考:C盘清理指南,清理出30G起,超详细总结&am…...

Excel中如何消除“长短款”
函数微调可以可以实施,简单且易于操作的气球🎈涨缩更妙。 (笔记模板由python脚本于2024年12月17日 06:19:13创建,本篇笔记适合用Excel操作数据的coder翻阅) 【学习的细节是欢悦的历程】 Python 官网:https://www.python.org/ Fre…...

超越 RAG 基础:AI 应用的高级策略
作者:来自 Elastic Elastic Platform Team 我们最近与 Cohere 举办的虚拟活动深入探讨了检索增强生成 (retrieval augmented generation - RAG) 的世界,重点讨论了在概念验证阶段之后构建 RAG 应用程序的关键注意事项。我们的演讲者是 Elastic 的首席解…...

[shader]【图形渲染】【unity】【游戏开发】 Shader数学基础2-认识点和矢量
在计算机图形学和Shader编程中,点和矢量是两种常见且基础的数学对象。它们在空间中的作用和性质是理解图形渲染的关键。本篇文章将深入探讨点(Point)和矢量(Vector)的定义、特性以及它们之间的关系。 1. 点(Point)的定义 在数学和计算机图形学中,**点(Point)**用于…...

微软开源Python Markdown转换工具
分享一个microsoft开源的Python工具——markitdown,轻松将各类文件转换为Markdown格式。 markitdown支持的文件格式 PDF(.pdf)PowerPoint(.pptx)Word(.docx)Excel(.xlsx)图片(支持EXIF元数据和OCR识别)音频(支持EXIF元数据和语音转录)HTML(包括对Wikipedia...

安装与配置MongoDB 6.0以支持远程连接
安装与配置MongoDB 6.0以支持远程连接 目录 安装curl工具下载并导入MongoDB 6.0 PGP密钥向APT导入MongoDB 6.0版软件包的资源链接安装MongoDB依赖libssl1.1安装MongoDB启动并检查MongoDB服务状态进入MongoDB Shell交互式执行环境设置MongoDB开机自启配置MongoDB允许远程连接 …...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
