【C++】sophus : geometry.hpp 位姿(SE2 和 SE3)和(2D 直线\3D 平面)转换函数 (五)
这段代码定义了一系列在位姿(SE2 和 SE3)和几何实体(2D 直线和 3D 平面)之间进行转换的函数。它利用了 Sophus 库中已有的旋转表示(SO2 和 SO3)。
以下是函数的详细解释:
1. SO2 与直线(2D):
normalFromSO2(SO2<T> const& R_foo_line):从旋转矩阵
R_foo_line中提取 y 轴作为参考系 "foo" 中的直线法向量。SO2FromNormal(Vector2<T> normal_foo):根据参考系 "foo" 中的直线法向量构造旋转矩阵
R_foo_line。
2. SO3 与平面(3D):
normalFromSO3(SO3<T> const& R_foo_plane):从旋转矩阵
R_foo_plane中提取 z 轴作为参考系 "foo" 中的平面法向量。rotationFromNormal(Vector3<T> const& normal_foo, ...):根据参考系 "foo" 中的平面法向量构造旋转矩阵
R_foo_plane。它还接受可选参数,用于提示平面参考系的 x 轴和 y 轴方向。此函数确保平面法向量不接近零,并检查提示方向之间的正交性。SO3FromNormal(Vector3<T> const& normal_foo):使用
rotationFromNormal从平面法向量创建 SO3 对象。
3. SE2 与直线(2D):
lineFromSE2(SE2<T> const& T_foo_line):从 2D 位姿
T_foo_line中提取直线信息。它使用normalFromSO2获取直线法向量,并使用平移分量作为到原点的距离。SE2FromLine(Line2<T> const& line_foo):根据参考系 "foo" 中的直线定义构造 2D 位姿
T_foo_line。它假设直线由其自身参考系的 x 轴定义。
4. SE3 与平面(3D):
planeFromSE3(SE3<T> const& T_foo_plane):从 3D 位姿
T_foo_plane中提取平面信息。它使用normalFromSO3获取平面法向量,并使用平移分量作为到原点的距离(沿负法向量方向)。SE3FromPlane(Plane3<T> const& plane_foo):根据参考系 "foo" 中的平面定义构造 3D 位姿
T_foo_plane。它假设平面由其自身参考系的 XY 平面定义。
5. 超平面:
makeHyperplaneUnique(Eigen::Hyperplane<T, N> const& plane):通过在必要时翻转法向量和偏移量以使偏移量为非负数,来确保超平面的唯一表示。
总而言之,这段代码提供了在 Sophus 库的位姿表示(SE2 和 SE3)的上下文中,表示和操作 2D 和 3D 空间中的直线和平面功能。它包含在这些表示之间进行转换的函数,并执行必要的有效性和唯一性检查。
简单来说,这段代码提供了一些数学工具函数,可以在位姿(包括位置和旋转)和几何对象(直线和平面)之间进行转换。比如,给定一个机器人的位姿,可以计算出它“看到”的某个平面的方程;反过来,给定一个平面的方程,也可以计算出一个和这个平面相关的位姿。这样做的好处是方便在机器人、计算机视觉等领域进行几何计算。
/// 变换位姿和超平面之间的关系。#pragma once // 防止头文件被重复包含#include "se2.hpp" // 导入 SE2 相关的头文件#include "se3.hpp" // 导入 SE3 相关的头文件#include "so2.hpp" // 导入 SO2 相关的头文件#include "so3.hpp" // 导入 SO3 相关的头文件#include "types.hpp" // 导入常用类型定义的头文件namespace Sophus { // 定义命名空间 Sophus/// 输入旋转 ``R_foo_plane``,返回沿 y 轴的对应直线法向量(在参考系 ``foo`` 中)。///template <class T>Vector2<T> normalFromSO2(SO2<T> const& R_foo_line) { return R_foo_line.matrix().col(1); // 返回旋转矩阵的第二列}/// 输入参考系 foo 中的直线法向量,构建对应的旋转矩阵 ``R_foo_line``。// 前置条件:``normal_foo`` 不能接近零。///template <class T>SO2<T> SO2FromNormal(Vector2<T> normal_foo) { SOPHUS_ENSURE(normal_foo.squaredNorm() > Constants<T>::epsilon(), "{}", normal_foo.transpose()); // 确保法向量的范数大于零 normal_foo.normalize(); // 归一化法向量 return SO2<T>(normal_foo.y(), -normal_foo.x()); // 返回旋转矩阵}/// 输入旋转 ``R_foo_plane``,返回沿 z 轴的对应平面法向量(在参考系 ``foo`` 中)。///template <class T>Vector3<T> normalFromSO3(SO3<T> const& R_foo_plane) { return R_foo_plane.matrix().col(2); // 返回旋转矩阵的第三列}/// 输入参考系 foo 中的平面法向量,构建对应的旋转矩阵 ``R_foo_plane``。// 注意:``plane`` 的坐标系定义为法向量沿正 z 轴指向。可以为 ``plane`` 坐标系的 x 轴和 y 轴指定提示。// 前置条件:/// - ``normal_foo``、``xDirHint_foo`` 和 ``yDirHint_foo`` 不能接近零。/// - ``xDirHint_foo`` 和 ``yDirHint_foo`` 必须大致垂直。///template <class T>Matrix3<T> rotationFromNormal(Vector3<T> const& normal_foo, Vector3<T> xDirHint_foo = Vector3<T>(T(1), T(0), T(0)), Vector3<T> yDirHint_foo = Vector3<T>(T(0), T(1), T(0))) { SOPHUS_ENSURE(xDirHint_foo.dot(yDirHint_foo) < Constants<T>::epsilon(), "xDirHint ({}) 和 yDirHint ({}) 必须垂直。", xDirHint_foo.transpose(), yDirHint_foo.transpose()); // 确保两个向量垂直 using std::abs; using std::sqrt; T const xDirHint_foo_sqr_length = xDirHint_foo.squaredNorm(); // 计算 xDirHint_foo 的平方范数 T const yDirHint_foo_sqr_length = yDirHint_foo.squaredNorm(); // 计算 yDirHint_foo 的平方范数 T const normal_foo_sqr_length = normal_foo.squaredNorm(); // 计算 normal_foo 的平方范数 SOPHUS_ENSURE(xDirHint_foo_sqr_length > Constants<T>::epsilon(), "{}", xDirHint_foo.transpose()); // 确保 xDirHint_foo 的范数大于零 SOPHUS_ENSURE(yDirHint_foo_sqr_length > Constants<T>::epsilon(), "{}", yDirHint_foo.transpose()); // 确保 yDirHint_foo 的范数大于零 SOPHUS_ENSURE(normal_foo_sqr_length > Constants<T>::epsilon(), "{}", normal_foo.transpose()); // 确保 normal_foo 的范数大于零 Matrix3<T> basis_foo; basis_foo.col(2) = normal_foo; // 将法向量设置为第三列 if (abs(xDirHint_foo_sqr_length - T(1)) > Constants<T>::epsilon()) { xDirHint_foo.normalize(); // 归一化 xDirHint_foo } if (abs(yDirHint_foo_sqr_length - T(1)) > Constants<T>::epsilon()) { yDirHint_foo.normalize(); // 归一化 yDirHint_foo } if (abs(normal_foo_sqr_length - T(1)) > Constants<T>::epsilon()) { basis_foo.col(2).normalize(); // 归一化法向量 } T abs_x_dot_z = abs(basis_foo.col(2).dot(xDirHint_foo)); // 计算法向量和 xDirHint_foo 的点积的绝对值 T abs_y_dot_z = abs(basis_foo.col(2).dot(yDirHint_foo)); // 计算法向量和 yDirHint_foo 的点积的绝对值 if (abs_x_dot_z < abs_y_dot_z) { // basis_foo.z 和 xDirHint_foo 不平行。 basis_foo.col(1) = basis_foo.col(2).cross(xDirHint_foo).normalized(); // 设置第二列为叉乘结果并归一化 basis_foo.col(0) = basis_foo.col(1).cross(basis_foo.col(2)); // 设置第一列为叉乘结果 } else { // basis_foo.z 和 yDirHint_foo 不平行。 basis_foo.col(0) = yDirHint_foo.cross(basis_foo.col(2)).normalized(); // 设置第一列为叉乘结果并归一化 basis_foo.col(1) = basis_foo.col(2).cross(basis_foo.col(0)); // 设置第二列为叉乘结果 } T det = basis_foo.determinant(); // 计算行列式 // 检查行列式是否为 1 SOPHUS_ENSURE(abs(det - T(1)) < Constants<T>::epsilon(), "基础的行列式不是 1,而是 {}。基础是 \n{}\n", det, basis_foo); return basis_foo; // 返回基础矩阵}/// 输入参考系 foo 中的平面法向量,构建对应的旋转矩阵 ``R_foo_plane``。// 详细信息请参阅 ``rotationFromNormal``。///template <class T>SO3<T> SO3FromNormal(Vector3<T> const& normal_foo) { return SO3<T>(rotationFromNormal(normal_foo)); // 调用 rotationFromNormal 函数并返回 SO3}/// 返回一个直线(相对于参考系 ``foo``),给定在参考系 ``foo`` 中的 ``line`` 的位姿。// 注意:平面由 ``line`` 坐标系的 X 轴定义。///template <class T>Line2<T> lineFromSE2(SE2<T> const& T_foo_line) { return Line2<T>(normalFromSO2(T_foo_line.so2()), T_foo_line.translation()); // 返回参数化直线}/// 返回位姿 ``T_foo_line``,给定参考系 ``foo`` 中的直线。// 注意:直线由 ``line`` 坐标系的 X 轴定义。///template <class T>SE2<T> SE2FromLine(Line2<T> const& line_foo) { T const d = line_foo.offset(); // 获取直线的偏移量 Vector2<T> const n = line_foo.normal(); // 获取直线的法向量 SO2<T> const R_foo_plane = SO2FromNormal(n); // 从法向量构建 SO2 return SE2<T>(R_foo_plane, -d * n); // 返回 SE2}/// 返回一个平面(相对于参考系 ``foo``),给定在参考系 ``foo`` 中的 ``plane`` 的位姿。// 注意:平面由 ``plane`` 坐标系的 XY 平面定义。///template <class T>Plane3<T> planeFromSE3(SE3<T> const& T_foo_plane) { return Plane3<T>(normalFromSO3(T_foo_plane.so3()), T_foo_plane.translation()); // 返回超平面}/// 返回位姿 ``T_foo_plane``,给定参考系 ``foo`` 中的平面。// 注意:平面由 ``plane`` 坐标系的 XY 平面定义。///template <class T>SE3<T> SE3FromPlane(Plane3<T> const& plane_foo) { T const d = plane_foo.offset(); // 获取平面的偏移量 Vector3<T> const n = plane_foo.normal(); // 获取平面的法向量 SO3<T> const R_foo_plane = SO3FromNormal(n); // 从法向量构建 SO3 return SE3<T>(R_foo_plane, -d * n); // 返回 SE3}/// 接收一个超平面,返回其唯一表示,确保 ``offset`` 为非负。///template <class T, int N>Eigen::Hyperplane<T, N> makeHyperplaneUnique(Eigen::Hyperplane<T, N> const& plane) { if (plane.offset() >= 0) { return plane; // 如果偏移量为非负,直接返回超平面 } return Eigen::Hyperplane<T, N>(-plane.normal(), -plane.offset()); // 否则,返回法向量和偏移量取反的超平面}} // namespace Sophus总结
normalFromSO2函数:
输入:SO2旋转矩阵
R_foo_line输出:对应的法向量,沿y轴方向
使用:用于提取旋转矩阵的第二列(y轴方向)
SO2FromNormal函数:
输入:参考系foo中的线法向量
normal_foo输出:对应的SO2旋转矩阵
注意:法向量
normal_foo必须归一化且不得接近零
normalFromSO3函数:
输入:SO3旋转矩阵
R_foo_plane输出:对应的平面法向量,沿z轴方向
使用:用于提取旋转矩阵的第三列(z轴方向)
rotationFromNormal函数:
输入:参考系foo中的平面法向量
normal_foo,以及x轴和y轴的提示方向输出:对应的3x3旋转矩阵
注意:
normal_foo,xDirHint_foo,yDirHint_foo必须归一化且不得接近零,且x轴和y轴方向必须垂直
SO3FromNormal函数:
输入:参考系foo中的平面法向量
normal_foo输出:对应的SO3旋转矩阵
使用:调用
rotationFromNormal函数并返回SO3对象
lineFromSE2函数:
输入:SE2姿态
T_foo_line输出:对应的线对象
使用:提取线的法向量和平移量
SE2FromLine函数:
输入:参考系foo中的线对象
line_foo输出:对应的SE2姿态
使用:提取线的法向量和偏移量,并计算其SE2姿态
planeFromSE3函数:
输入:SE3姿态
T_foo_plane输出:对应的平面对象
使用:提取平面的法向量和平移量
SE3FromPlane函数:
输入:参考系foo中的平面对象
plane_foo输出:对应的SE3姿态
使用:提取平面的法向量和偏移量,并计算其SE3姿态
makeHyperplaneUnique函数:
输入:超平面
plane输出:唯一表示的超平面,确保偏移量不为负
使用:将法向量和偏移量取负,以确保偏移量不为负
这段代码实现了姿态和超平面之间的各种转换函数,包括从旋转矩阵提取法向量、从法向量构建旋转矩阵、从SE2/SE3姿态构建线/平面对象,以及确保超平面的唯一表示。通过这些转换函数,可以方便地在姿态和几何对象之间进行转换,提高代码的可读性和可维护性。
相关文章:
和(2D 直线\3D 平面)转换函数 (五))
【C++】sophus : geometry.hpp 位姿(SE2 和 SE3)和(2D 直线\3D 平面)转换函数 (五)
这段代码定义了一系列在位姿(SE2 和 SE3)和几何实体(2D 直线和 3D 平面)之间进行转换的函数。它利用了 Sophus 库中已有的旋转表示(SO2 和 SO3)。 以下是函数的详细解释: 1. SO2 与直线…...
获取时间)
moment()获取时间
moment 是一个 JavaScript 日期处理类库。 使用: //安装 moment npm install moment -- save引用 //在main.js中全局引入 import moment from "moment"设定moment区域为中国 //import 方式 import moment/locale/zh-cn moment.locale(zh-cn); 挂载全…...

Azure虚拟机非托管磁盘大小调整
想要扩容一个Azure VM 的磁盘空间,门户里面竟然无法扩展,点点鼠标就完事的时代在离去,微软越来不想微软。 在门户里面即便使用Azure Cli命令行也不行。 PS /home/gpchina> az disk list [] 返回为空,根本没有返回磁盘。 不过使…...

流匹配模型[Flow Matching]
流匹配模型:概念、优缺点与扩散模型的对比 在生成建模领域,流匹配模型(Flow Matching)是一种通过学习流场将初始分布(通常是高斯噪声)变换为目标分布的新型框架。本文将对流匹配模型的概念、与扩散模型的联…...

Unix 和 Windows 的有趣比较
Unix 和 Windows NT 比较 来源于这两本书,把两本书对照来读,发现很多有意思的地方: 《Unix 传奇》 https://book.douban.com/subject/35292726/ 《观止 微软创建NT和未来的夺命狂奔 》 Showstopper!: The Breakneck Race to Create Windows…...
——贪心算法)
算法(三)——贪心算法
文章目录 定义基本原理基本思路优缺点优点缺点 经典案例及解析找零问题问题描述贪心思路算法解析java代码示例 活动选择问题问题描述贪心思路算法解析java代码示例 车辆路径问题问题描述贪心思路算法分析java代码示例 定义 贪心算法是指在求解问题时,总是做出在当前…...

LeetCode 704.二分查找
LeetCode 704.二分查找 思路🧐: 在本篇以及之后几篇的博客中,博主将会用二分法进行解答,以此巩固二分题型。二分法一般用于具有二段性的数据中使用。比如该题为有序数组,需要我们查找一个目标值target,分析…...
Linux介绍与安装CentOS 7操作系统
什么是操作系统 操作系统,英⽂名称 Operating System,简称 OS,是计算机系统中必不 可少的基础系统软件,它是 应⽤程序运⾏以及⽤户操作必备的基础环境 ⽀撑,是计算机系统的核⼼。 操作系统的作⽤是管理和控制计算机系…...

使用 rbenv 切换 Ruby 版本
1. 查看当前 Ruby 版本 首先,查看当前系统中安装的 Ruby 版本: ruby -v如果你已经安装了 rbenv,可以列出通过 rbenv 安装的 Ruby 版本: rbenv versions2. 安装 Ruby 版本 如果你想安装新的 Ruby 版本,使用以下命令…...
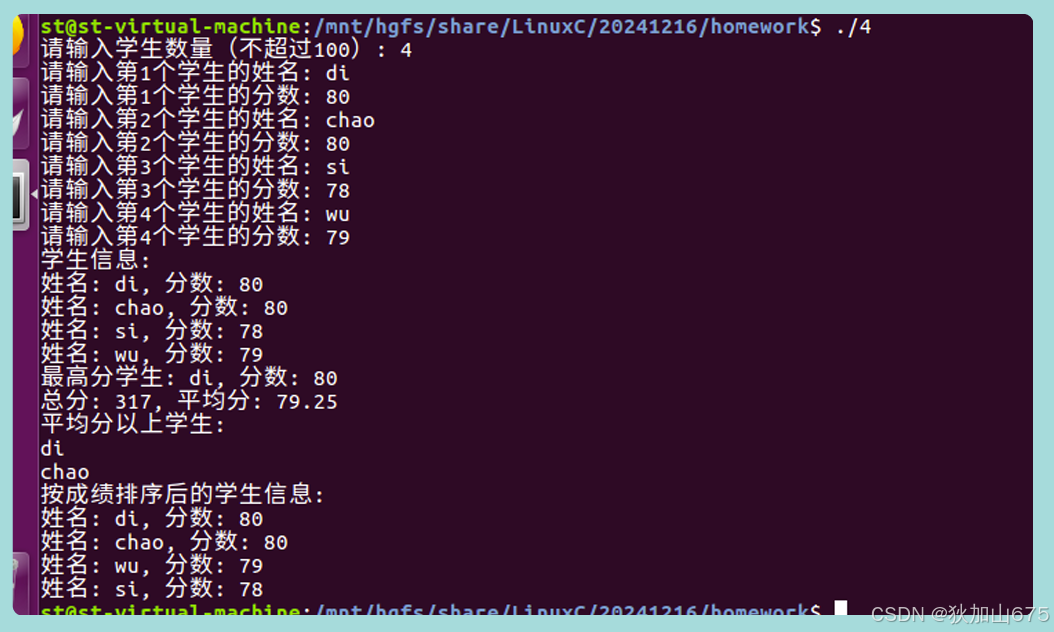
C语言(结构体练习)
设计一个结构体,存放一个学员信息并显示,存放两个学员信息,算他们的平均分。 #include <stdio.h> #include <string.h>// 定义结构体 typedef struct {char name[50];float score; } Student;// 函数声明 void display(Student student); f…...

你了解网络层的 ICMP 吗?
你了解网络层的 ICMP 吗? 一. 什么是 ICMP二. ICMP 的工作原理三. ICMP 的结构四. ICMP 的常见应用五. ICMP 的局限性与安全性六. 总结 前言 这是我在这个网站整理的笔记,有错误的地方请指出,关注我,接下来还会持续更新。 作者:神…...
清理C盘小记
突然C盘就爆满了,想当初还是给他预留了120G的空间,感觉到现在也不够用了,担心出现死机的情况就赶紧进行了清理。有一说一,清理回收站是真的有用。 参考:C盘清理指南,清理出30G起,超详细总结&am…...

Excel中如何消除“长短款”
函数微调可以可以实施,简单且易于操作的气球🎈涨缩更妙。 (笔记模板由python脚本于2024年12月17日 06:19:13创建,本篇笔记适合用Excel操作数据的coder翻阅) 【学习的细节是欢悦的历程】 Python 官网:https://www.python.org/ Fre…...

超越 RAG 基础:AI 应用的高级策略
作者:来自 Elastic Elastic Platform Team 我们最近与 Cohere 举办的虚拟活动深入探讨了检索增强生成 (retrieval augmented generation - RAG) 的世界,重点讨论了在概念验证阶段之后构建 RAG 应用程序的关键注意事项。我们的演讲者是 Elastic 的首席解…...

[shader]【图形渲染】【unity】【游戏开发】 Shader数学基础2-认识点和矢量
在计算机图形学和Shader编程中,点和矢量是两种常见且基础的数学对象。它们在空间中的作用和性质是理解图形渲染的关键。本篇文章将深入探讨点(Point)和矢量(Vector)的定义、特性以及它们之间的关系。 1. 点(Point)的定义 在数学和计算机图形学中,**点(Point)**用于…...

微软开源Python Markdown转换工具
分享一个microsoft开源的Python工具——markitdown,轻松将各类文件转换为Markdown格式。 markitdown支持的文件格式 PDF(.pdf)PowerPoint(.pptx)Word(.docx)Excel(.xlsx)图片(支持EXIF元数据和OCR识别)音频(支持EXIF元数据和语音转录)HTML(包括对Wikipedia...

安装与配置MongoDB 6.0以支持远程连接
安装与配置MongoDB 6.0以支持远程连接 目录 安装curl工具下载并导入MongoDB 6.0 PGP密钥向APT导入MongoDB 6.0版软件包的资源链接安装MongoDB依赖libssl1.1安装MongoDB启动并检查MongoDB服务状态进入MongoDB Shell交互式执行环境设置MongoDB开机自启配置MongoDB允许远程连接 …...

零衍门户国际化:助力拓展全球视野
概述 零衍系统管理平台统一门户管理,支持门户看板灵活配置,同时提供场景化的门户模板,丰富的门户组件,可协助用户快速搭建企业专属门户。 随着零衍产品的不断成熟,国际化需求日益增多,客户期望零衍门户可…...

mysql免安装版配置教程
一、将压缩包解压至你想要放置的文件夹中,注意:绝对路径中要避免出现中文 二、在解压目录下新建my.ini文件,已经有的就直接覆盖 my.ini文件内容 [mysqld] # 设置3306端口 port3306 # 设置mysql的安装目录 basedirD:\\tools\\mysql-8.1.0-win…...

kafka的处理的一些问题 消费延迟
kafka的处理的一些问题 消费者客户端不但没有背压而且内存充足,但产生的消费延迟越来越大在Kafka的Leader副本宕机时 消费者客户端不但没有背压而且内存充足,但产生的消费延迟越来越大 比如我们这个kakfa集群一共有3个Broker节点 TOp1有5个分区…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
