Python 的 Decimal的错误计算
摘要 阐述在使用 Python的 Decimal类时,可能产生的错误计算。
在 详述 BigDecimal 的错误计算 中,笔者较为详细地说明了 Java的 BigDecimal可能出错的原因。类似地,Python的 decimal模块中有个 Decimal类,也可用于高精度的十进制运算,并且能够避免由于浮点数表示不精确带来的精度问题。但是,相仿地,由于有一些参数要设置,所以亦会出现参数不同结果不一致现象。
例1. 不妨重新讨论 计算机的错误计算(一百七十七)中多项式(稍作修改:将小数部分去掉,变成整数)。
已知
计算
代码如下:
from decimal import Decimal, getcontext
base = Decimal(234) # 定义基数
terms = [ # 计算每一项Decimal(134450) * base ** 12,Decimal(-31470000) * base ** 11,Decimal(2030000) * base ** 10,Decimal(1350000) * base ** 9,Decimal(1680000) * base ** 8,Decimal(1120000) * base ** 7,Decimal(748000) * base ** 6,Decimal(187000) * base ** 5,Decimal(46800) * base ** 4,Decimal(-140) * base ** 2,Decimal(7666044)]
print(sum(terms)) # 计算总和,输出结果这时,输出为 1381004:

然而,准确值是 204 . 因此,代码输出的是错误结果。
例2. 用 Python的 Decimal编程计算
代码如下(来源于一大模型):
from decimal import Decimal, getcontextgetcontext().prec = 50 # 设置精度,这里设置为50位小数base = Decimal('23.67') # 定义数值
exponent = Decimal('65.5')part1 = base ** exponent # 计算 23.67^65.5part2 = (exponent * base.ln()).exp() # 计算 exp(65.5 * ln(23.67))result = part1 - part2 # 计算差值print(result)运行后,输出为 -1E+41(显然是错误结果。正确值是0):

另外,getcontext().prec 不同,那么输出也不同。
点评:
(1)例1可以通过提高精度获得正确结果。
(2)例2不行。
(3)对于例1,虽然可以通过提高精度获得正确值,但是,用户不确定究竟 getcontext().prec 设为多少。只能是通过实验进行猜测。正像有学者评价数学软件一样:“The multiprecision ... in Mathematica and Maple is not very useful ..., because the working precision must be specified by the user and this naturally implies some guess work”[1]。
(4)getcontext().prec 的默认值是28 . 因此,例1中所有运算的结果应该是保留28位十进制有效数字。
参考文献
[1] Cuyt A, Verdonk B, Becuwe S, et al. A remarkable example of catastrophic cancellation unraveled. Computing, 2001, 66: 309–320
相关文章:

Python 的 Decimal的错误计算
摘要 阐述在使用 Python的 Decimal类时,可能产生的错误计算。 在 详述 BigDecimal 的错误计算 中,笔者较为详细地说明了 Java的 BigDecimal可能出错的原因。类似地,Python的 decimal模块中有个 Decimal类,也可用于高精度的十进制…...

【韩顺平 Java满汉楼项目 控制台版】MySQL+JDBC+druid
文章目录 功能界面用户登录界面显示餐桌状态预定显示所有菜品点餐查看账单结账退出满汉楼 程序框架图项目依赖项目结构方法调用图功能实现登录显示餐桌状态订座显示所有菜品点餐查看账单结账退出满汉楼 扩展思考多表查询如果将来字段越来越多怎么办? 员工信息字段可…...

【HAL库】STM32CubeMX开发----STM32F407----Time定时器中断实验
STM32CubeMX 下载和安装 详细教程 【HAL库】STM32CubeMX开发----STM32F407----目录 前言 本次实验以 STM32F407VET6 芯片为MCU,使用 25MHz 外部时钟源。 实现定时器TIM3中断,每1s进一次中断。 定时器计算公式如下: arr 是自动装载值&#x…...
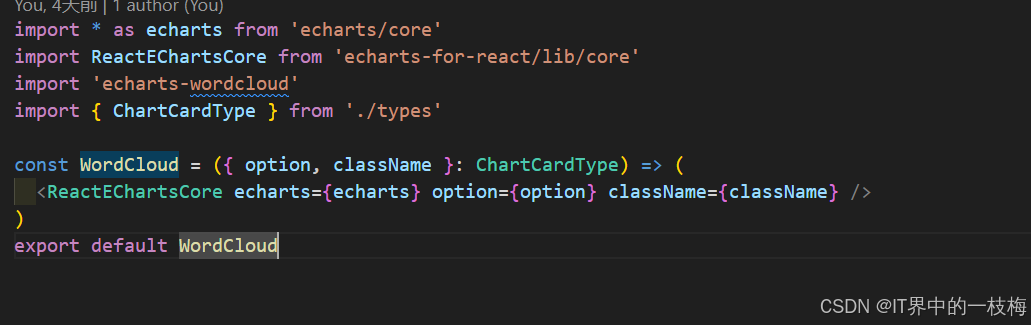
react18+ts 封装图表及词云组件
react18ts 封装图表及词云组件 1.下载依赖包 "echarts": "^5.5.1","echarts-for-react": "^3.0.2","echarts-wordcloud": "^2.1.0",2.创建目录结构 3.代码封装 ChartCard.tsx Wordcloud.tsx 4.调用 import Rea…...

图像根据mask拼接时,边缘有色差 解决
目录 渐变融合(Feathering) 沿着轮廓线模糊: 代码: 泊松融合 效果比较好: 效果图: 源代码: 泊松融合,mask不扩大试验 效果图: 源代码: 两个图像根据mask拼接时,边缘有色差 渐变融合(Feathering) import numpy as np import cv2# 假设 img1, img2 是两个…...

17、ConvMixer模型原理及其PyTorch逐行实现
文章目录 1. 重点2. 思维导图 1. 重点 patch embedding : 将图形分割成不重叠的块作为图片样本特征depth wise point wise new conv2d : 将传统的卷积转换成通道隔离卷积和像素空间隔离两个部分,在保证精度下降不多的情况下大大减少参数量 2. 思维导图 后续再整…...

Spring整合Redis基本操作步骤
Spring 整合 Redis 操作步骤总结 1. 添加依赖 首先,在 pom.xml 文件中添加必要的 Maven 依赖。Redis 相关的依赖包括 Spring Boot 的 Redis 启动器和 fastjson(如果需要使用 Fastjson 作为序列化工具): <!-- Spring Boot Re…...

STM32使用SFUD库驱动W25Q64
SFUD简介 SFUD是一个通用SPI Flash驱动库,通过SFUD可以库轻松完成对SPI Flash的读/擦/写的基本操作,而不用自己去看手册,写代码造轮子。但是SFUD的功能不仅仅于此:①通过SFUD库可以实现在一个项目中对多个Flash的同时驱动&#x…...

ArKTS基础组件
一.AlphabetIndexer 可以与容器组件联动用于按逻辑结构快速定位容器显示区域的组件。 子组件 color:设置文字颜色。 参数名类型必填说明valueResourceColor是 文字颜色。 默认值:0x99182431。 selectedColor:设置选中项文字颜色。 参数名类型必填说明valueRes…...

如何理解TCP/IP协议?如何理解TCP/IP协议是什么?
理解TCP/IP协议 1. 什么是TCP/IP协议? TCP/IP(Transmission Control Protocol/Internet Protocol,传输控制协议/网际协议)是一组用于实现网络通信的协议,广泛用于互联网和局域网中。TCP/IP协议栈由一系列协议组成,规定了计算机如何在网络中发送和接收数据。它通常被用来…...

如何使用 Python 连接 SQLite 数据库?
SQLite是一种轻量级的嵌入式数据库,广泛应用于各种应用程序中。 Python提供了内置的sqlite3模块,使得连接和操作SQLite数据库变得非常简单。 下面我将详细介绍如何使用sqlite3模块来连接SQLite数据库,并提供一些实际开发中的建议和注意事项…...
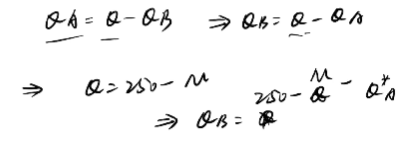
【博弈模型】古诺模型、stackelberg博弈模型、伯特兰德模型、价格领导模型
博弈模型 1、古诺模型(cournot)(1)假设(2)行为分析(3)经济后果(4)例题 2、stackelberg博弈模型(产量领导模型)(1ÿ…...
)
单片机:实现花样灯数码管的显示(附带源码)
单片机实现花样灯数码管显示 数码管(七段数码管)广泛用于数字显示,例如时钟、计数器、温度计等设备。在本项目中,我们将使用单片机实现花样灯数码管的显示效果。所谓花样灯显示是指通过控制数码管上的各个段位,以不同…...
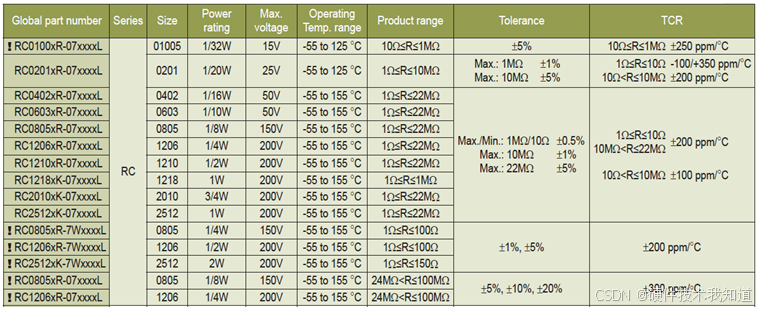
什么是芯片电阻
有人把Chip Resistor翻译成“芯片电阻”,我觉得翻译成“贴片电阻”或“片状电阻”更合适。有些厂商也称之为”电阻片”,英文写作Resistor Chip。比如:Thick film resistor chips(厚膜电阻片)、Thin film resistor chip…...
和(2D 直线\3D 平面)转换函数 (五))
【C++】sophus : geometry.hpp 位姿(SE2 和 SE3)和(2D 直线\3D 平面)转换函数 (五)
这段代码定义了一系列在位姿(SE2 和 SE3)和几何实体(2D 直线和 3D 平面)之间进行转换的函数。它利用了 Sophus 库中已有的旋转表示(SO2 和 SO3)。 以下是函数的详细解释: 1. SO2 与直线…...
获取时间)
moment()获取时间
moment 是一个 JavaScript 日期处理类库。 使用: //安装 moment npm install moment -- save引用 //在main.js中全局引入 import moment from "moment"设定moment区域为中国 //import 方式 import moment/locale/zh-cn moment.locale(zh-cn); 挂载全…...

Azure虚拟机非托管磁盘大小调整
想要扩容一个Azure VM 的磁盘空间,门户里面竟然无法扩展,点点鼠标就完事的时代在离去,微软越来不想微软。 在门户里面即便使用Azure Cli命令行也不行。 PS /home/gpchina> az disk list [] 返回为空,根本没有返回磁盘。 不过使…...

流匹配模型[Flow Matching]
流匹配模型:概念、优缺点与扩散模型的对比 在生成建模领域,流匹配模型(Flow Matching)是一种通过学习流场将初始分布(通常是高斯噪声)变换为目标分布的新型框架。本文将对流匹配模型的概念、与扩散模型的联…...

Unix 和 Windows 的有趣比较
Unix 和 Windows NT 比较 来源于这两本书,把两本书对照来读,发现很多有意思的地方: 《Unix 传奇》 https://book.douban.com/subject/35292726/ 《观止 微软创建NT和未来的夺命狂奔 》 Showstopper!: The Breakneck Race to Create Windows…...
——贪心算法)
算法(三)——贪心算法
文章目录 定义基本原理基本思路优缺点优点缺点 经典案例及解析找零问题问题描述贪心思路算法解析java代码示例 活动选择问题问题描述贪心思路算法解析java代码示例 车辆路径问题问题描述贪心思路算法分析java代码示例 定义 贪心算法是指在求解问题时,总是做出在当前…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...
