2012年西部数学奥林匹克试题(几何)
2012/G1

△ A B C \triangle ABC △ABC 内有一点 P P P, P P P 在 A B AB AB, A C AC AC 上的投影分别为 E E E, F F F, 射线 B P BP BP, C P CP CP 分别交 △ A B C \triangle ABC △ABC 的外接圆于点 M M M, N N N. r r r 为 △ A B C \triangle ABC △ABC 的内切圆半径, R R R 为 △ A B C \triangle ABC △ABC 的外接圆半径. 求证: E F / M N ≥ r / R EF/MN \geq r/R EF/MN≥r/R.
证明: 设 P P P 在 B C BC BC 上的投影为点 D D D.设 S S S 为 S △ A B C S_{\triangle ABC} S△ABC. 延长 A P AP AP 交 ( A B C ) (ABC) (ABC) 于点 L L L.

当 P P P 位于内心 I I I 时, 易证明 E F EF EF 在 ( A B C ) (ABC) (ABC) 中, M N MN MN 在 ⨀ I \bigodot I ⨀I 中所对的圆周角 (锐角) 大小都为 π / 2 − A / 2 \pi/2-A/2 π/2−A/2. 此时 E F / M N = r / R EF/MN=r/R EF/MN=r/R.

下证当 P P P 不位于内心位置时, E F / M N > r / R EF/MN>r/R EF/MN>r/R.
△ L M N ∼ △ D E F \triangle LMN \sim \triangle DEF △LMN∼△DEF (证明略), 进而 E F / M N = r ′ / R EF/MN=r'/R EF/MN=r′/R. ( r ′ r' r′ 为 ( D E F ) (DEF) (DEF) 的半径), 要证明 E F / M N > r / R EF/MN>r/R EF/MN>r/R, 只需证明 r ′ > r r'>r r′>r.

设 △ D E F \triangle DEF △DEF 的外心为 O ′ O' O′.
S = S △ O ′ A B + S △ O ′ A C + S △ O ′ B C = 1 2 ( B C ⋅ d (
相关文章:

2012年西部数学奥林匹克试题(几何)
2012/G1 △ A B C \triangle ABC △ABC 内有一点 P P P, P P P 在 A B AB AB, A C AC AC 上的投影分别为 E E E, F F F, 射线 B P BP BP, C P CP CP 分别交 △ A B C \triangle ABC △ABC 的外接圆于点 M M M, N N N. r r r 为 △ A B C \triangle ABC △ABC 的内…...

8位移位寄存器的verilog语言
module shift_register (output reg [7:0] Q, // 8位移位寄存器输出input D, // 输入数据input rst, // 复位信号input clk // 时钟信号 );always (posedge clk) beginif (!rst)Q < 8b00000000; // 复位时将Q清零elseQ < {Q[6:0], D}; // 否则…...

【苍穹外卖】学习心得体会-随笔
前言 写了很久,终于可以完整运行项目了,记录下这几天的心得体会回顾一下知识点 第一天、Git 分布式版本控制工具 一、Git概述 定义:是分布式版本控制工具,用于管理软件开发中的源代码文件,像Java类、xml文件、html…...

MySQL学习之表的增删改
MySQL学习之表的增删改 语法总结: INSERT INTO 表名 (字段名1, 字段名2, ...) VALUES (值1, 值2, ...); //指定字段添加数据 INSERT INTO 表名 VALUES (值1, 值2, ...); //给全部字段添加数据 INSERT INTO 表名 VALUES (值1, 值2, ...), (值1, 值2, ...), (值1, …...
电脑excel词典(xllex.dll)文件丢失是或损坏是什么原因?“xllex.dll文件缺失“要怎么解决?
Excel词典(xllex.dll)文件丢失或损坏?别担心,这里有解决之道! 在日常的电脑使用和办公软件操作中,我们偶尔会碰到一些让人头疼的问题,比如Excel突然提示“Excel词典(xllex.dll&…...

【CSS in Depth 2 精译_084】第 14 章:CSS 蒙版、形状与剪切概述 + 14.1:CSS 滤镜
当前内容所在位置(可进入专栏查看其他译好的章节内容) 第四部分 视觉增强技术 ✔️【第 14 章 蒙版、形状与剪切】 ✔️ 14.1 滤镜 ✔️ 14.1.1 滤镜的类型 ✔️14.1.2 背景滤镜 ✔️ 14.2 蒙版 文章目录 第 14 章 蒙版、形状与剪切 Masks, shapes, and…...

gorm源码解析(四):事务,预编译
文章目录 前言事务自己控制事务用 Transaction方法包装事务 预编译事务结合预编译总结 前言 前几篇文章介绍gorm的整体设计,增删改查的具体实现流程。本文将聚焦与事务和预编译部分 事务 自己控制事务 用gorm框架,可以自己控制事务的Begin࿰…...

前端优雅(装逼)写法(updating····)
1.>>右位移运算符取整数 它将一个数字的二进制位向右移动指定的位数,并在左侧填充符号位(即负数用1填充,正数用0填充)。 比如 2.99934 >> 0:取整结果是2,此处取整并非四舍五入 2.99934 会先…...

黑马Java面试教程_P7_常见集合_P4_HashMap
系列博客目录 文章目录 系列博客目录4. HashMap相关面试题4.4 面试题-HashMap的put方法的具体流程 频54.4.1 hashMap常见属性4.4.2 源码分析 HashMap的构造函数面试文稿: 4.5 讲一讲HashMap的扩容机制 难3频4面试文稿: 4.6 面试题-hashMap的寻址算法 难4…...

使用 CFD 加强水资源管理:全面概述
探索 CFD(计算流体动力学)在增强保护人类健康的土木和水利工程实践方面的重大贡献。 挑战 水资源管理是指规划、开发、分配和管理水资源最佳利用的做法。它包括广泛的活动,旨在确保水得到有效和可持续的利用,以满足各种需求&…...

XXE练习
pikachu-XXE靶场 1.POC:攻击测试 <?xml version"1.0"?> <!DOCTYPE foo [ <!ENTITY xxe "a">]> <foo>&xxe;</foo> 2.EXP:查看文件 <?xml version"1.0"?> <!DOCTYPE foo [ <!ENTITY xxe SY…...

R语言读取hallmarks的gmt文档的不同姿势整理
不同格式各有所用 1.读取数据框格式的 hallmarks <- clusterProfiler::read.gmt("~/genelist/h.all.v7.4.symbols.gmt") #返回的是表格 hallmarks$term<- gsub(HALLMARK_,"",hallmarks$term)适配Y叔的clusterProfiler的后续分析,比如整理后geneli…...

【Nginx-4】Nginx负载均衡策略详解
在现代Web应用中,随着用户访问量的增加,单台服务器往往难以承受巨大的流量压力。为了解决这一问题,负载均衡技术应运而生。Nginx作为一款高性能的Web服务器和反向代理服务器,提供了多种负载均衡策略,能够有效地将请求分…...

Python 的 Decimal的错误计算
摘要 阐述在使用 Python的 Decimal类时,可能产生的错误计算。 在 详述 BigDecimal 的错误计算 中,笔者较为详细地说明了 Java的 BigDecimal可能出错的原因。类似地,Python的 decimal模块中有个 Decimal类,也可用于高精度的十进制…...

【韩顺平 Java满汉楼项目 控制台版】MySQL+JDBC+druid
文章目录 功能界面用户登录界面显示餐桌状态预定显示所有菜品点餐查看账单结账退出满汉楼 程序框架图项目依赖项目结构方法调用图功能实现登录显示餐桌状态订座显示所有菜品点餐查看账单结账退出满汉楼 扩展思考多表查询如果将来字段越来越多怎么办? 员工信息字段可…...

【HAL库】STM32CubeMX开发----STM32F407----Time定时器中断实验
STM32CubeMX 下载和安装 详细教程 【HAL库】STM32CubeMX开发----STM32F407----目录 前言 本次实验以 STM32F407VET6 芯片为MCU,使用 25MHz 外部时钟源。 实现定时器TIM3中断,每1s进一次中断。 定时器计算公式如下: arr 是自动装载值&#x…...
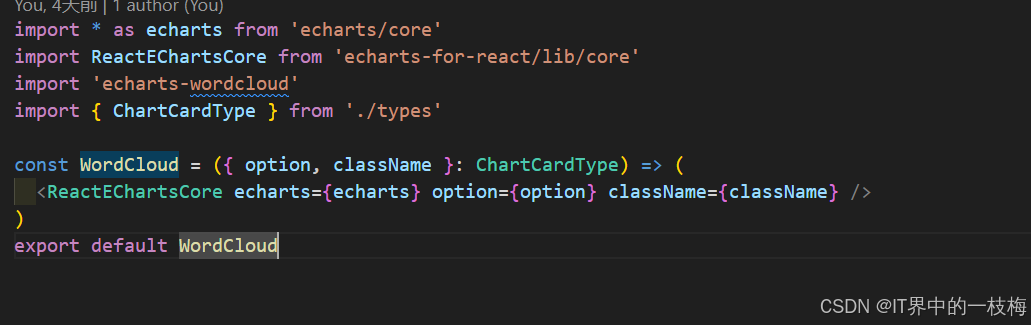
react18+ts 封装图表及词云组件
react18ts 封装图表及词云组件 1.下载依赖包 "echarts": "^5.5.1","echarts-for-react": "^3.0.2","echarts-wordcloud": "^2.1.0",2.创建目录结构 3.代码封装 ChartCard.tsx Wordcloud.tsx 4.调用 import Rea…...

图像根据mask拼接时,边缘有色差 解决
目录 渐变融合(Feathering) 沿着轮廓线模糊: 代码: 泊松融合 效果比较好: 效果图: 源代码: 泊松融合,mask不扩大试验 效果图: 源代码: 两个图像根据mask拼接时,边缘有色差 渐变融合(Feathering) import numpy as np import cv2# 假设 img1, img2 是两个…...

17、ConvMixer模型原理及其PyTorch逐行实现
文章目录 1. 重点2. 思维导图 1. 重点 patch embedding : 将图形分割成不重叠的块作为图片样本特征depth wise point wise new conv2d : 将传统的卷积转换成通道隔离卷积和像素空间隔离两个部分,在保证精度下降不多的情况下大大减少参数量 2. 思维导图 后续再整…...

Spring整合Redis基本操作步骤
Spring 整合 Redis 操作步骤总结 1. 添加依赖 首先,在 pom.xml 文件中添加必要的 Maven 依赖。Redis 相关的依赖包括 Spring Boot 的 Redis 启动器和 fastjson(如果需要使用 Fastjson 作为序列化工具): <!-- Spring Boot Re…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
