牛客周赛 Round 72 题解
本次牛客最后一个线段树之前我也没碰到过,等后续复习到线段树再把那个题当例题发出来
小红的01串(一)

思路:正常模拟,从前往后遍历一遍去统计即可
#include<bits/stdc++.h>
using namespace std;
#define int long long
string s;
int a[4];
signed main()
{cin>>s;int ans=0;for(int i=1;i<s.size();i++){if(s[i-1]=='0'&&s[i]=='1'){ans++;;}if(s[i-1]=='1'&&s[i]=='0'){ans++;;}}cout<<ans;
}小红的01串(二)

思路:我们找一下规律,我们发现长度为2的只有1个,长度为3的可以有3个,长度为4的会有6个,所以规律就是长度为n的01交替序列,能产生的值为(1+n-1)*n/2;
然后直接去统计即可
#include <iostream>
#include <string>
using namespace std;
#define int long long
signed main() {string s;cin >> s;int n = s.size();int result = 0;int length = 1;for (int i = 1; i < n; ++i) {if (s[i] != s[i - 1]) {length++; } else {if (length >= 2) {result += (length - 1) * length / 2;}length = 1; }}if (length>=2) {result += (length - 1) * length / 2;}cout << result << endl;return 0;
}小红的01串(三)

思路:我们首先来分析一下什么时候会是不可能存在的,最大的相邻01子串应当为2*min(a,b)前提是大的要比小的至少多1
然后剩下的就是看k的奇偶性,如果是奇数,那么a,b用的一样多,否则就是大的比小的多用一个
但是呢注意特判,因为有可能为0,如果为0的话,只有a,b同时都不为0,那就是不可能构造出来的,看代码吧
#include<bits/stdc++.h>
using namespace std;
#define int long long
int t;
int a,b,k;
void solve()
{cin>>a>>b>>k;if(k==0&&a!=0&&b!=0){cout<<"-1\n";return ;}if(2*min(a,b)<k){cout<<"-1\n";return ;}else{if(k%2==1){int x=(k+1)/2;a-=x;b-=x;for(int i=1; i<=a; i++){cout<<0;}for(int i=1; i<=x; i++){cout<<"01";}for(int i=1; i<=b; i++){cout<<1;}cout<<"\n";}else{k-=1;int x=(k+1)/2;a-=x;b-=x;if(a>b){a-=1;if(a<0){cout<<-1<<"\n";return ;}for(int i=1; i<=a; i++){cout<<0;}for(int i=1; i<=x; i++){cout<<"01";}for(int i=1; i<=b; i++){cout<<1;}cout<<"0";cout<<"\n";}else{b-=1;if(b<0){cout<<-1<<"\n";return ;}cout<<"1";for(int i=1; i<=a; i++){cout<<0;}for(int i=1; i<=x; i++){cout<<"01";}for(int i=1; i<=b; i++){cout<<1;}cout<<"\n";}}}
}
signed main()
{cin>>t;while(t--){solve();}return 0;
}
小红的01串(四)

思路:我们可以先去找到右边和当前元素相同和不同的位置,然后跑dp,dp[i]表示到i位置所花的最小花费是多少
ps:dp数组初始化大一点,因为开的太小了,所以导致赛时没过
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,x,y;
string s;
int a[100005];
int same[100005];
int differ[100005];
int dp[100005];
signed main()
{cin>>n>>x>>y;cin>>s;s=' '+s;for(int i=1;i<=n;i++){same[i]=-1;differ[i]=-1;}memset(dp,0x3f,sizeof(dp));dp[1]=0;int num[2]={-1,-1};for(int i=n;i>=1;i--){if(s[i]=='1'){same[i]=num[1];differ[i]=num[0];}else{same[i]=num[0];differ[i]=num[1];}num[s[i]-'0']=i;}for(int i=1;i<=n;i++){if(same[i]!=-1){dp[same[i]]=min(dp[same[i]],dp[i]+x);}if(differ[i]!=-1){dp[differ[i]]=min(dp[differ[i]],dp[i]+y);}}cout<<dp[n];return 0;
}小红的01串(五)

思路:dp[i][j]表示,选完前i个位置,取模13余j的个数,那么我们就可以发现找到dp转移公式,假设此次后面加上add这个数,那么整题值变化为整体值*10+add
因此dp转移方程为
dp[i+1][(j*10+add)%13]=(dp[i+1][(j*10+add)%13]+dp[i][j])%mod;
#include<bits/stdc++.h>
using namespace std;
#define int long long
string s;
int dp[200005][13];
int mod=1000000007;
signed main()
{cin>>s;int n=s.size();dp[0][0]=1;for(int i=0;i<n;i++){for(int j=0;j<13;j++){if(dp[i][j]==0){continue;}if(s[i]=='0'||s[i]=='1'){int add=s[i]-'0';dp[i+1][(j*10+add)%13]=(dp[i+1][(j*10+add)%13]+dp[i][j])%mod;}else {for(int add=0;add<=1;add++){dp[i+1][(j*10+add)%13]=(dp[i+1][(j*10+add)%13]+dp[i][j])%mod;}}}}cout<<dp[n][0];return 0;
}
相关文章:

牛客周赛 Round 72 题解
本次牛客最后一个线段树之前我也没碰到过,等后续复习到线段树再把那个题当例题发出来 小红的01串(一) 思路:正常模拟,从前往后遍历一遍去统计即可 #include<bits/stdc.h> using namespace std; #define int lo…...

Flux Tools 结构简析
Flux Tools 结构简析 BFL 这次一共发布了 Canny、Depth、Redux、Fill 四个 Tools 模型系列,分别对应我们熟悉的 ControlNets、Image Variation(IP Adapter)和 Inpainting 三种图片条件控制方法。虽然实现功能是相同的,但是其具体…...

0 前言
ArCS作为一个基于Rust的CAD(计算机辅助设计)开源系统,尽管已经有四年未更新,但其设计理念和技术实现仍然具有很高的学习和参考价值。以下是对ArCS项目的进一步分析和解读: 一、项目亮点与技术优势 高效与安全的Rust语…...

ARM嵌入式学习--第八天(PWM)
PWM -PWM介绍 PWM(pulse Width Modulation)简称脉宽调制,是利用微处理器的数字输出来对模拟电路进行控制的一种非常有效的技术,广泛应用在测量,通信,工控等方面 PWM的频率 是指在1秒钟内,信号从…...

遇到“REMOTE HOST IDENTIFICATION HAS CHANGED!”(远程主机识别已更改)的警告
连接虚拟机时提示报错: [insocoperhq-soc-cap-raw3 ~]$ ssh root10.99.141.104WARNING: REMOTE HOST IDENTIFICATION HAS CHANGED! IT IS POSSIBLE THAT SOMEONE IS DOING SOMETHING NASTY! Someone could be eavesdropping on you right now (man-in-the-midd…...

vue3前端组件库的搭建与发布(一)
前言: 最近在做公司项目中,有这么一件事情,很是头疼,就是同一套代码,不同项目,要改相同bug,改好多遍,改的都想吐,于是就想做一个组件库,这样更新一下就全都可…...

COMSOL快捷键及内置函数
文章目录 COMSOL快捷键使用COMSOL算子求最大值和最小值COMSOL内置函数3.1 解析函数3.2 插值函数3.3 分段函数3.4 高斯脉冲函数3.5 斜坡函数3.6 矩形函数3.7 波形函数3.8 随机函数3.9 Matlab函数3.10 SWITCH函数 COMSOL快捷键 Ctrl+/ 可快速打开预定义的物理量列表。…...
HUAWEI-eNSP交换机链路聚合(手动负载分担模式)
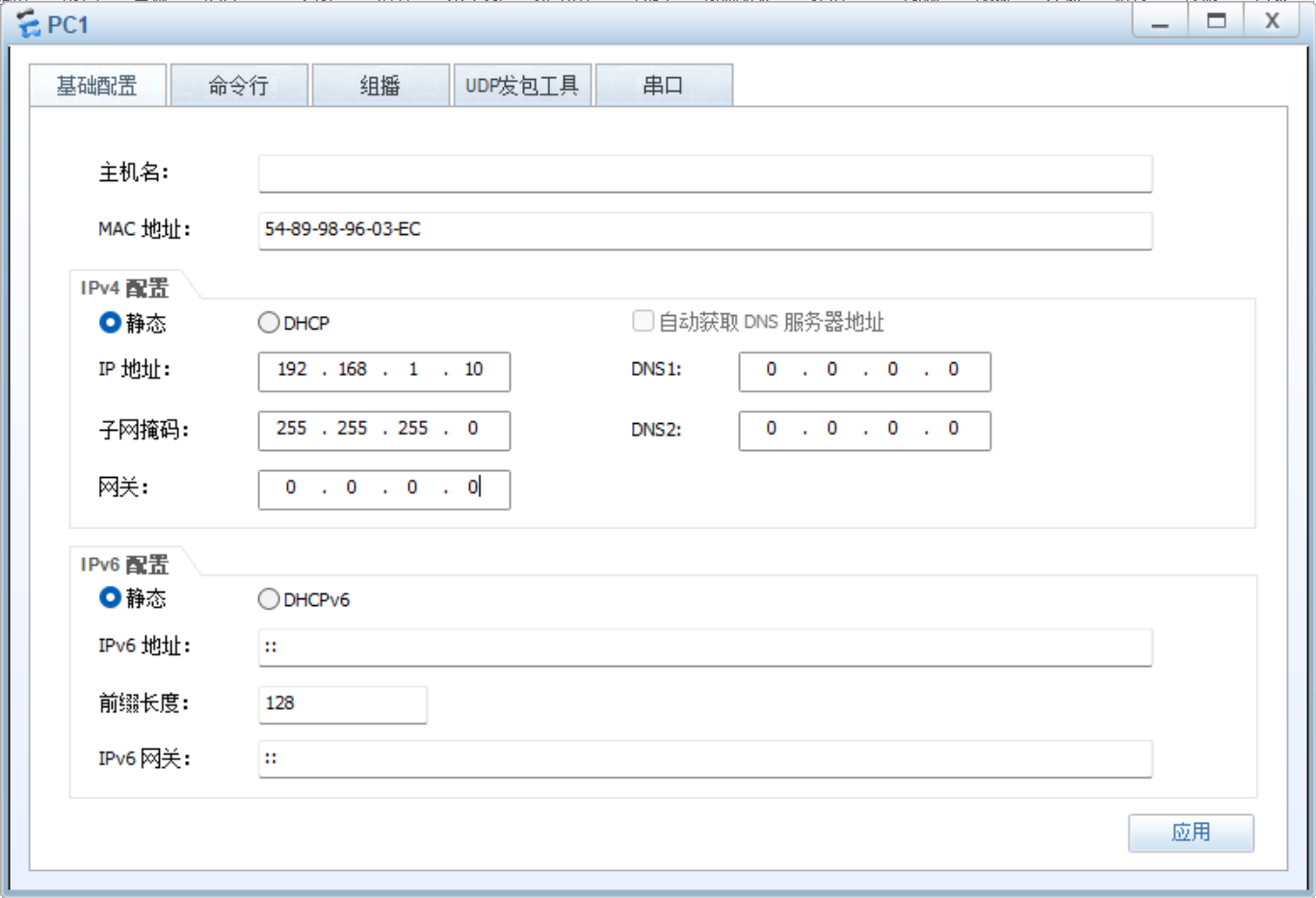
配置思路:HUAWEI交换机链路聚合有LACP模式跟手动负载分担模式,本文主打手动负载分担模式:首先交换机-PC之间划分基本vlan,交换机-交换机之间创建链路聚合组,划分端口至链路聚合分组(缺省模式为手动负载分担模式)。结果验证要求同vlan可以ping通,关闭某个聚合端口后仍可…...

番外篇 | Hyper-YOLO:超图计算与YOLO架构相结合成为目标检测新的SOTA !
前言:Hello大家好,我是小哥谈。Hyper-YOLO,该方法融合了超图计算以捕捉视觉特征之间复杂的高阶关联。传统的YOLO模型虽然功能强大,但其颈部设计存在局限性,限制了跨层特征的融合以及高阶特征关系的利用。Hyper-YOLO在骨干和颈部的联合增强下,成为一个突破性的架构。在COC…...

【MATLAB第109期】基于MATLAB的带置信区间的RSA区域敏感性分析方法,无目标函数
【MATLAB第108期】基于MATLAB的带置信区间的RSA区域敏感性分析方法,无目标函数 参考第64期文章【MATLAB第64期】【保姆级教程】基于MATLAB的SOBOL全局敏感性分析模型运用(含无目标函数,考虑代理模型) 创新点: 1、采…...

Bootstrap 表格
Bootstrap 表格 引言 Bootstrap 是一个流行的前端框架,它提供了一套丰富的工具和组件,用于快速开发响应式和移动设备优先的网页。在本文中,我们将重点讨论 Bootstrap 中的表格组件,包括其基本结构、样式以及如何使用 Bootstrap …...

【论文阅读】Computing the Testing Error without a Testing Set
https://blog.csdn.net/qq_40021158/article/details/109485216 可以使用测试集来估计训练集和测试集之间的性能差距,但是要避免过度拟合测试数据几乎是不可能的。 使用隔离的测试集可能会解决此问题,但这需要不断更新数据集,这是一项非常昂贵…...

Visio——同一个工程导出的PDF文件大小不一样的原因分析
现象 在不同电脑,导出来的PDF文件大小不一样。 原因分析 文件小的未将字体嵌入,文件大的已经将字体嵌入了。...

【ETCD】ETCD 架构揭秘:内部各组件概览
ETCD 的主要组件及它们之间的关联关系如下: 目录 1. Client(客户端)2. gRPC 接口3. Etcd Server Main Loop(ETCD 主循环)4. Raft(共识模块)5. Peer Etcd Nodes(ETCD 集群节点&#x…...
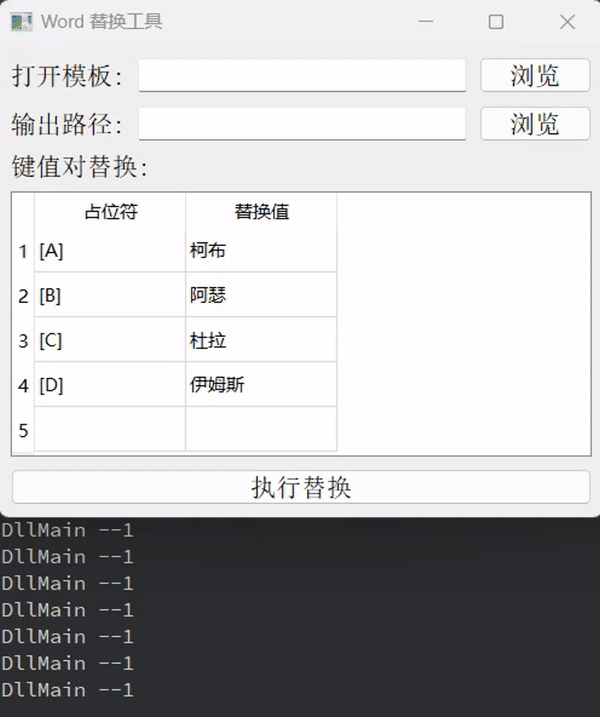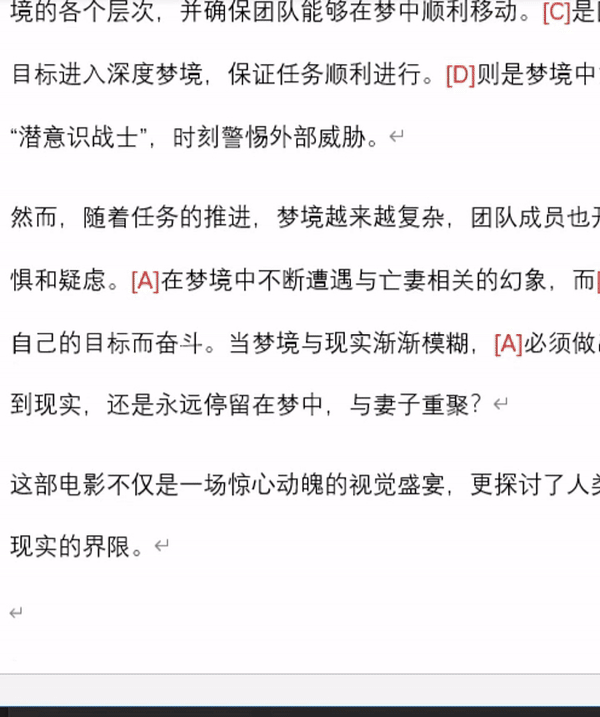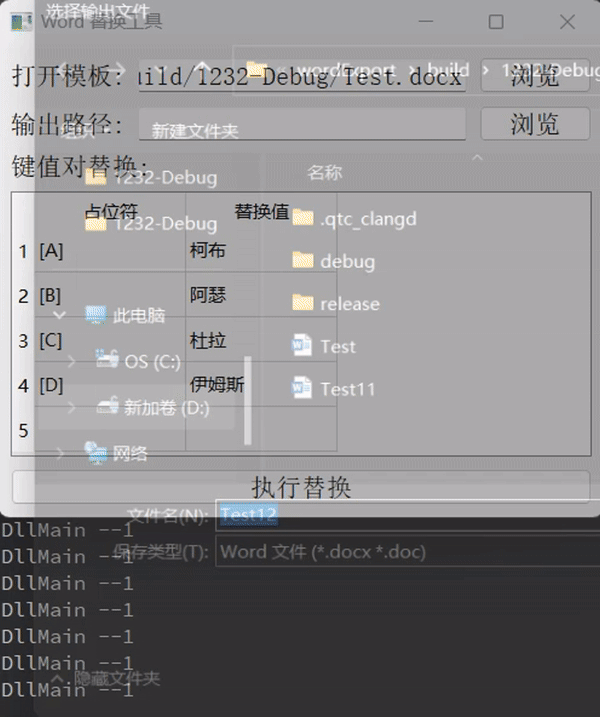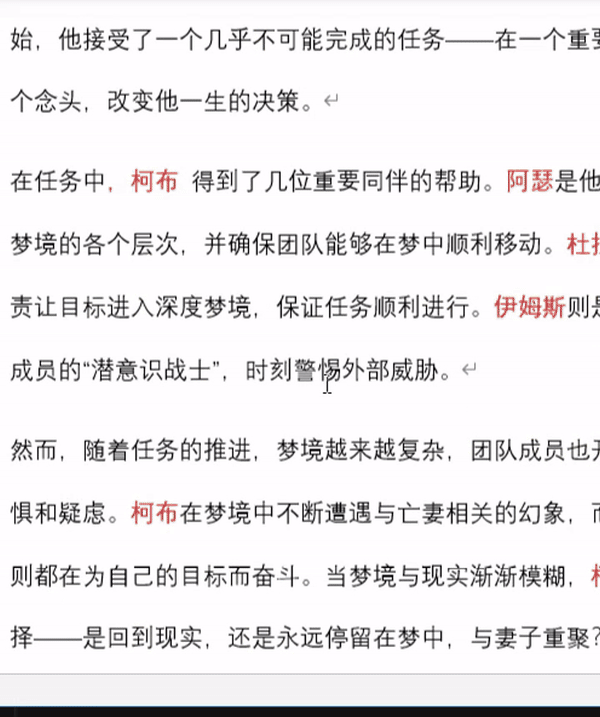
Qt WORD/PDF(四)使用 QAxObject 对 Word 替换(QWidget)
关于QT Widget 其它文章请点击这里: QT Widget 国际站点 GitHub: https://github.com/chenchuhan 国内站点 Gitee : https://gitee.com/chuck_chee 姊妹篇: Qt WORD/PDF(一)使用 QtPdfium库实现 PDF 操作 Qt WORD/PDF(二…...
:hls协议)
音视频学习(二十四):hls协议
基本原理 HLS协议通过将视频文件切分成多个小的媒体段(通常是10秒左右的.ts文件),并通过HTTP传输给客户端。视频播放过程中,客户端按顺序请求这些小段文件来逐步播放整个视频流。HLS还支持多种码率,以便适应不同网络条…...

UniDepth 学习笔记
摘要 准确的单目度量深度估计(MMDE)是解决三维感知和建模中下游任务的关键。然而,最近的MMDE方法的显著准确性仅限于其训练领域。这些方法存在适度的域间隙,也不能推广到看不见的域,这阻碍了它们的实际适用性。本文提出…...

PVE——OpenWRT 硬盘 size单位的调整
问题:初始状态为120MB 还需要进行计算,如果通过图形界面添加磁盘会出现单位不变的情况。 进入命令行前记得给你的虚拟机拍照,防止误操作 通过ssh 进入PVE命令行 按需添加容量即可 不到1G 会显示M 超过1G 不是G整数均为M单位。 …...

Android-ImagesPickers 拍照崩溃优化
Android-ImagesPickers 作为老牌图片选择器,帮助了很多牛马宝宝,刚好最近用到了多相册选择以及拍照,可能是高版本机型问题,导致拍照后就闪退 原作者文章以及git Android实用视图动画及工具系列之九:漂亮的图片选择器…...
)
Linux dd 命令详解:工作原理与实用指南(C/C++代码实现)
这段代码是一个模仿 Linux dd 命令的工具,它用于在不同文件之间复制数据。dd 是一个非常强大的命令行工具,可以用于数据备份、转换和复制。下面我将详细解释这段代码的原理、实现方式以及如何运行和测试。 Linux dd 命令的工作原理 dd 命令是 Unix 和 …...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...
