稀疏矩阵的存储与计算 gaxpy
1, gaxpy 数学公式
其中: ,
,
2, 具体实例
3,用稠密矩阵的方法
本节将用于验证第4节中的稀疏计算的结果
hello_gaxpy_dense.cpp
#include <stdio.h>
#include <stdlib.h>struct Matrix_SP
{float* val; // 矩阵中非零元素,按列收集在一起;int* c; // 某列非零元素开始的index in val[...];int* r; // val中每个元素的行号;int M;int N;
};void gen_sparse_matrix(int m, int n, float* A, int lda)
{//step1, randomfor(int i=0; i<m; i++){for(int j=0; j<n; j++){if((1.0*rand())/RAND_MAX < 0.6f)A[i + j*lda] = 0.0f;elseA[i + j*lda] = (1.0*rand())/RAND_MAX;}}
}void print_matrix(int m, int n, float* A, int lda)
{for(int i=0; i<m; i++){for(int j=0; j<n; j++){printf(" %7.4f", A[i + j*lda]);}printf("\n");}
}void gemm_cc(int M, int N, int K, float alpha, float*A, int lda, float* B, int ldb, float beta, float* C, int ldc)
{for(int i=0; i<M; i++){for(int j=0; j<N; j++){float sigma = 0.0f;for(int k=0; k<K; k++){sigma += A[i + k*lda]*B[k + j*ldb];}C[i + j*ldc] = alpha*sigma + beta*C[i + j*ldc];}}
}int main()
{int m = 6;int n = 5;int lda = m;// y and x are column vector;//y(6) = y(6) + A(6,5) * x(5)^t;float* y = NULL;float* x = NULL;float* A = NULL;A = (float*)malloc(lda*n*sizeof(float));y = (float*)malloc(m*sizeof(float));x = (float*)malloc(n*sizeof(float));//step 0, gen dense matrix;gen_sparse_matrix(m, n, A, lda);print_matrix(m, n, A, lda);//step 1, make dense matrix sparse;//step 2, gen y;//step 3, gen x;//step 4, dense gaxpy// 4.1 tmp = Ax;//4.2 y = y + tmp;//step 5, sparse gaxpy// 5.1 tmp = Ax// 5.2 y = y + tmp;free(A);free(y);free(x);return 0;
}
Makefile
all: g.outg.out: hello_dense_sparse_gaxpy.cppg++ -g $< -o $@.PHONY: clean
clean:-rm -rf g.out4,用稀疏矩阵的方法
存储A
4.1 压缩列表示法
struct Matrix_SP
{float* val; // 矩阵中非零元素,按列收集在一起;int* c; // 某列非零元素开始的index in val[...];int* r; // val中每个元素的行号;int M;int N;
};struct Matrix_SP 用于存储一个稀疏矩阵;
现在来用它存储 第2节 中的A矩阵;
4.2 稀疏 gemv 计算
相关文章:
稀疏矩阵的存储与计算 gaxpy
1, gaxpy 数学公式 其中: , , 2, 具体实例 3,用稠密矩阵的方法 本节将用于验证第4节中的稀疏计算的结果 hello_gaxpy_dense.cpp #include <stdio.h> #include <stdlib.h>struct Matrix_SP {float* val; //…...
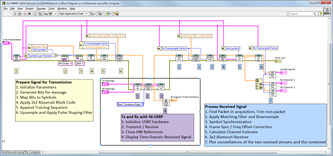
基于LabVIEW的USRP信道测量开发
随着无线通信技术的不断发展,基于软件无线电的设备(如USRP)在信道测量、无线通信测试等领域扮演着重要角色。通过LabVIEW与USRP的结合,开发者可以实现信号生成、接收及信道估计等功能。尽管LabVIEW提供了丰富的信号处理工具和图形…...
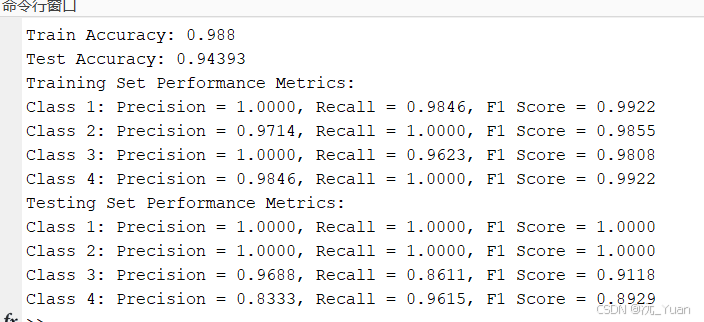
基于LSTM长短期记忆神经网络的多分类预测【MATLAB】
在深度学习中,长短期记忆网络(LSTM, Long Short-Term Memory)是一种强大的循环神经网络(RNN)变体,专门为解决序列数据中的长距离依赖问题而设计。LSTM因其强大的记忆能力,广泛应用于自然语言处理…...
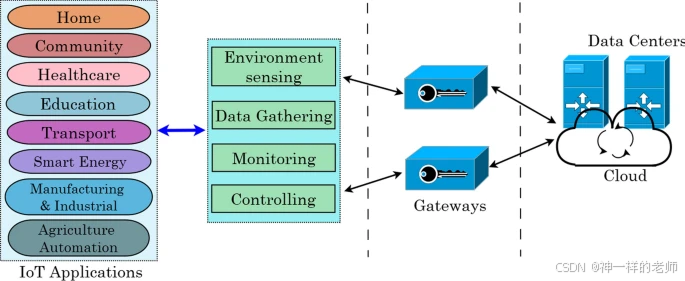
物联网:全面概述、架构、应用、仿真工具、挑战和未来方向
中文论文标题:物联网:全面概述、架构、应用、仿真工具、挑战和未来方向 英文论文标题:Internet of Things: a comprehensive overview, architectures, applications, simulation tools, challenges and future directions 作者信息&#x…...
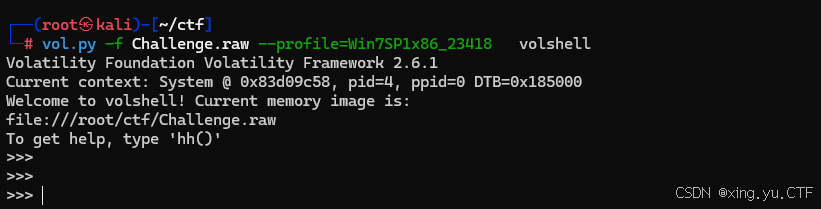
volatility2工具的使用vol2工具篇
vol2工具 命令格式:vol.py -f [image] --profile[profile] [plugin] 1、查看系统的操作版本,系统镜像信息 2.查看用户名密码信息,当前操作系统中的password hash,例如SAM文件内容 3.从注册表提取LSA密钥信息(已解密&…...

R 基础运算
R 基础运算 R 是一种广泛使用的统计编程语言,它提供了强大的数据操作和分析功能。基础运算在 R 中非常重要,因为它们是进行更复杂计算和数据分析的基础。本文将详细介绍 R 中的基础运算,包括算术运算、逻辑运算、向量化和矩阵运算。 一、算…...
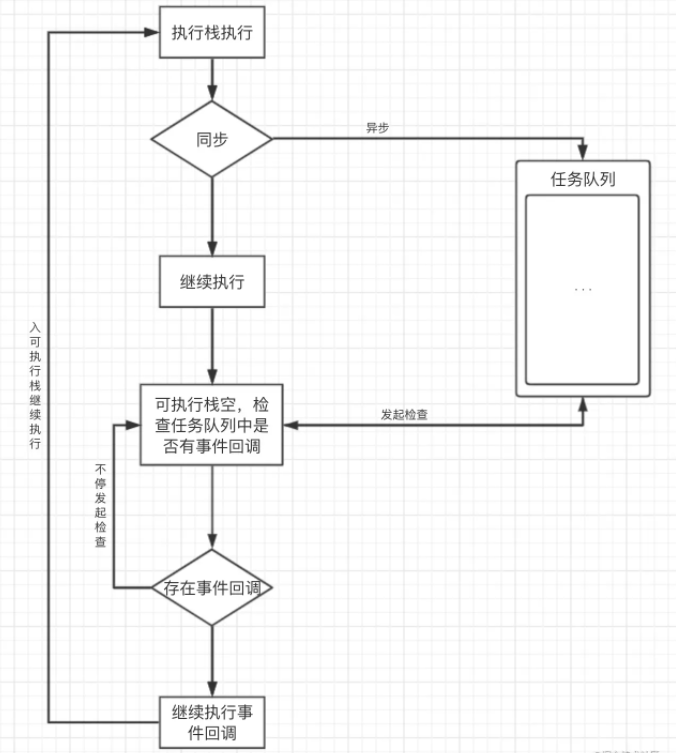
javaScriptBOM
1.1、BOM概述 1.1.1、BOM简介 BOM(browser Object)即浏览器对象模型,它提供了独立于内容而与浏览器窗口进行交互的对象,其核心对象是window。 BOM由一系列的对象构成,并且每个对象都提供了很多方法与属性 BOM缺乏标准…...

Godot RPG 游戏开发指南
Godot RPG 游戏开发指南 一、基础准备 1. 开发环境 下载并安装最新版 Godot 4.x选择使用 GDScript 或 C# 作为开发语言准备基础美术资源(角色、地图、道具等) 2. 项目结构 project/ ├── scenes/ # 场景文件 ├── scripts/ # 脚…...

目标检测数据集图片及标签同步旋转角度
前言 在深度学习领域,尤其是目标检测任务中,数据集的质量直接影响模型的性能。为了提升模型的鲁棒性和对各种场景的适应能力,数据增强技术被广泛应用于图像数据集处理。旋转角度是常见的数据增强方法,通过对图像及其对应的标签&am…...

2025前端面试热门题目——计算机网络篇
计算机网络篇——面试 1. 到底什么是 TCP 连接? TCP 连接的定义 TCP(传输控制协议)是一个面向连接的传输层协议。TCP 连接是通过 三次握手 确立的可靠数据通信链路,保证了在不可靠网络(如互联网)上的数据传输的准确…...

LEAST-TO-MOST PROMPTING ENABLES COMPLEX REASONING IN LARGE LANGUAGE MODELS---正文
题目 最少到最多的提示使大型语言模型能够进行复杂的推理 论文地址:https://arxiv.org/abs/2205.10625 摘要 思路链提示在各种自然语言推理任务中表现出色。然而,它在需要解决比提示中显示的示例更难的问题的任务上表现不佳。为了克服这种由易到难的概括…...
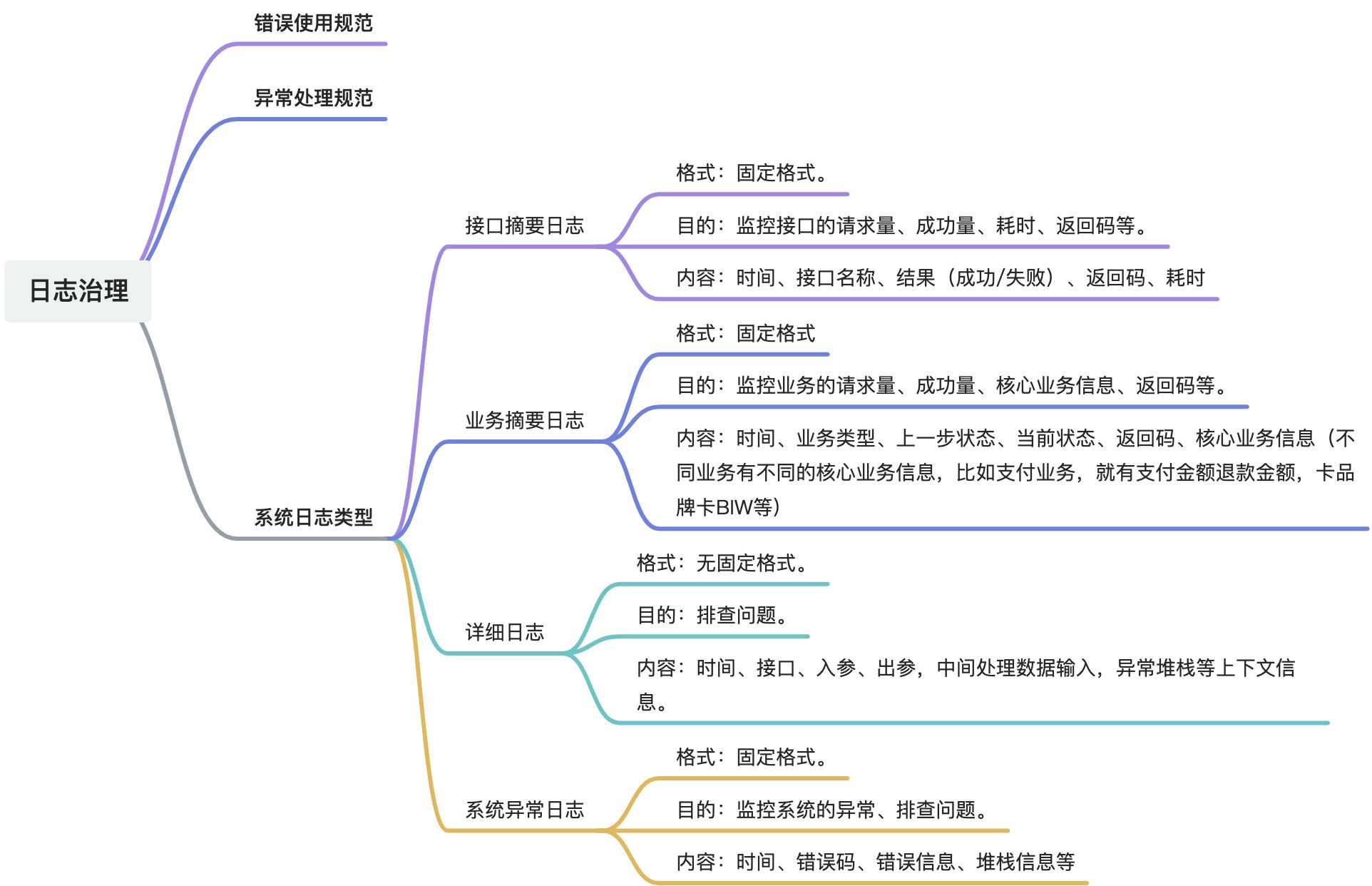
Java开发经验——日志治理经验
摘要 本文主要介绍了Java开发中的日志治理经验,包括系统异常日志、接口摘要日志、详细日志和业务摘要日志的定义和目的,以及错误码规范和异常处理规范。强调了日志治理的重要性和如何通过规范化错误码和日志格式来提高系统可观测性和问题排查效率。 1. …...
使用复数类在C#中轻松绘制曼德布洛集分形
示例在 C# 中绘制曼德布洛特集分形解释了如何通过迭代以下方程来绘制曼德布洛特集: 其中 Z(n) 和 C 是复数。程序迭代此方程,直到 Z(n) 的大小至少为 2 或程序执行最大迭代次数。 该示例在单独的变量中跟踪数字的实部和虚部。此示例使用Complex类来更轻松…...
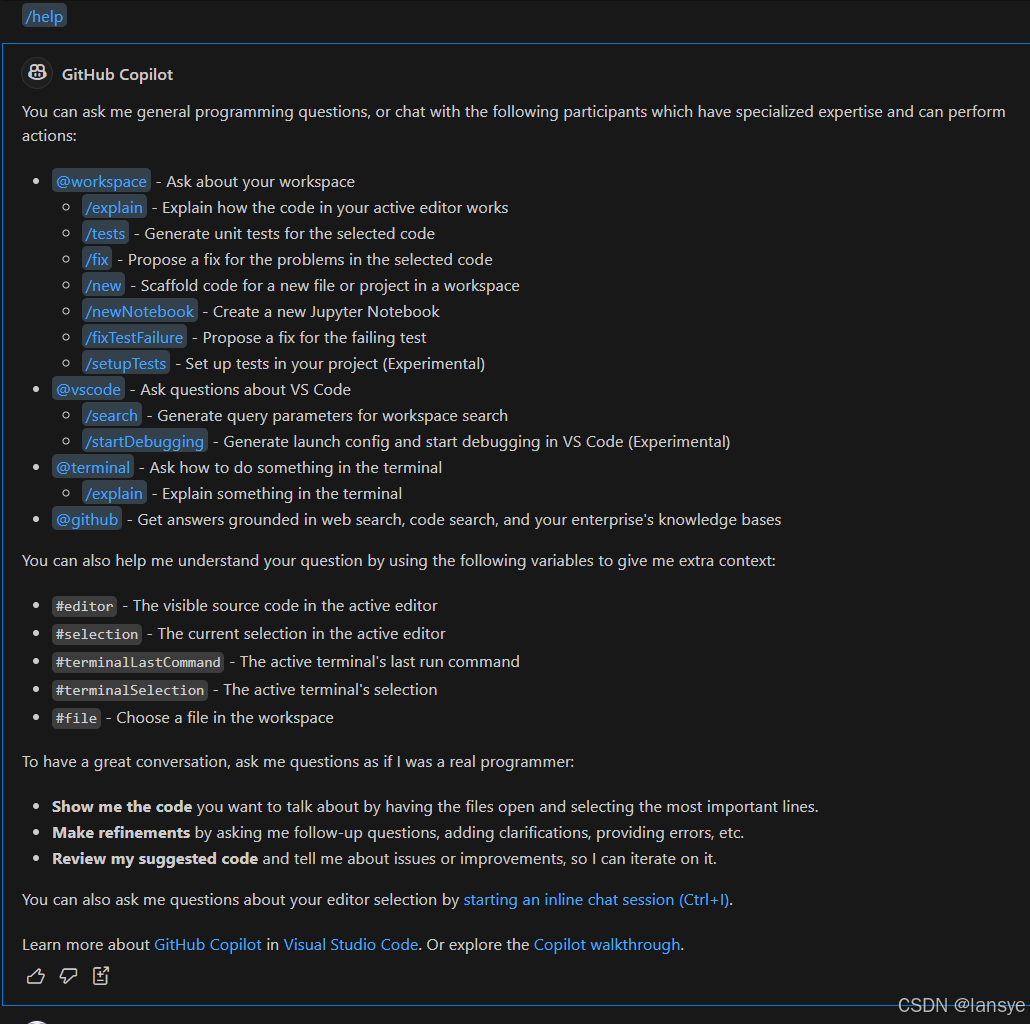
VSCode 启用免费 Copilot
升级VSCode到 1.96版本,就可以使用每个月2000次免费额度了,按照工作日每天近80次免费额度,满足基本需求。前两天一直比较繁忙,今天周六有时间正好体验一下。 引导插件安装GitHub Copilot - Visual Studio Marketplace Extension f…...

常见问题整理
DevOps 和 CICD DevOps 全称Development & Operation 一种实现开发和运维一体化的协同模式,提供快速交付应用和服务的能力 用于协作:开发,部署,质量测试 整体生命周期工作内容,最终实现持续继承,持续部…...

使用Vue创建前后端分离项目的过程(前端部分)
前端使用Vue.js作为前端开发框架,使用Vue CLI3脚手架搭建项目,使用axios作为HTTP库与后端API交互,使用Vue-router实现前端路由的定义、跳转以及参数的传递等,使用vuex进行数据状态管理,后端使用Node.jsexpress…...

【Springboot知识】Redis基础-springboot集成redis相关配置
文章目录 1. 添加依赖2. 配置Redis连接3. 配置RedisTemplate(可选)4. 使用RedisTemplate或StringRedisTemplate5. 测试和验证 集群配置在application.properties中配置在application.yml中配置 主从配置1. 配置Redis服务器使用配置文件使用命令行 2. 配置…...

网络安全概论——身份认证
一、身份证明 身份证明可分为以下两大类 身份验证——“你是否是你所声称的你?”身份识别——“我是否知道你是谁?” 身份证明系统设计的三要素: 安全设备的系统强度用户的可接受性系统的成本 实现身份证明的基本途径 所知:个…...

OpenHarmony-4.HDI 框架
HDI 框架 1.HDI介绍 HDI(Hardware Device Interface,硬件设备接口)是HDF驱动框架为开发者提供的硬件规范化描述性接口,位于基础系统服务层和设备驱动层之间,是连通驱动程序和系统服务进行数据流通的桥梁,是…...

leecode494.目标和
这道题目第一眼感觉就不像是动态规划,可以看出来是回溯问题,但是暴力回溯超时,想要用动态规划得进行一点数学转换 class Solution { public:int findTargetSumWays(vector<int>& nums, int target) {int nnums.size(),bagWeight0,s…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...
