【Java】二叉树
一、树形结构
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
- 有一个特殊的节点,称为根节点,根节点没有前驱节点;
- 除根节点外,其余节点被分成M(M > 0)个互不相交的集合T1、T2、…、Tm,其中每一个集合 Ti (1 <= i<= m)又是一棵与树类似的子树。
- 每棵子树的根节点有且只有一个前驱,可以有0个或多个后继;
- 树是递归定义的。
相关概念
- 节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的度为3;
- 树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为3;
- 叶子节点或终端节点:度为0的节点称为叶节点; 如上图:E、F、I…等节点为叶节点;
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点;
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点;
- 根结点:一棵树中,没有双亲结点的结点;如上图:A
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
- 非终端节点或分支节点:度不为0的节点; 如上图:B、C、D、G节点为分支节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C、D是兄弟节点;
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、J互为兄弟节点;
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先;
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙;
- 森林:由m(m>=0)棵互不相交的树的集合称为森林。
二、二叉树
2.1 概念
一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
2.2 二叉树的特点:
- 每个结点最多有两棵子树,即二叉树不存在度大于2的结点。
- 二叉树的子树有左右之分,其子树的次序不能颠倒。
2.3 特殊的二叉树
(1)满二叉树:
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
(2)完全二叉树:
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
PS:完全二叉树的底部是连续的,满二叉树一定是完全二叉树
2.4 二叉树的性质
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2i-1 (i>0)个结点;
- 若规定只有根节点的二叉树的深度为1,则深度为K的二叉树的最大结点数是2k-1 (k>=0); 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1;
- 具有n个结点的完全二叉树的深度k为log2(n+1) 上取整;
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i的结点有:
- 若i>0,双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点;
- 若2i+1<n,左孩子序号:2i+1,否则无左孩子;
- 若2i+2<n,右孩子序号:2i+2,否则无右孩子;
如:假设一棵完全二叉树中总共有1000个节点,则该二叉树中__500___个叶子节点,__500___个非叶子节点,__1___个节点只有左孩子,__0___个只有右孩子。
题解:将该二叉树节点缩小100倍,变为该完全二叉树中总共有10个节点,由性质2可得深度K为:4,前三层共有7个节点,则最后一层有10-7=3个节点,由性质1的第三层有4个节点,其中有2个节点上面有子节点,剩余2个为叶子结点,则该二叉树共有3+2=5个叶子结点,扩大100倍为500个叶子结点,则剩余的就位非叶子结点。有相关分析可知该二叉树有1个节点只有左孩子,0个节点只有右孩子。
2.5 二叉树的存储
二叉树的存储结构分为:顺序存储和类似于链表的链式存储。
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式,具体如下:
// 孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}// 孩子双亲表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
Node parent; // 当前节点的根节点
}2.6 二叉树的遍历
遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题(比如:打印节点内容、节点内容加1)。
遍历是二叉树上最重要的操作之一,是二叉树上进行其它运算之基础。
在遍历二叉树时,如果没有进行某种约定,每个人都按照自己的方式遍历,得出的结果就比较混乱,如果按照某种规则进行约定,则每个人对于同一棵树的遍历结果肯定是相同的。
如果N代表根节点,L代表根节点的左子树,R代表根节点的右子树,则根据遍历根节点的先后次序有以下遍历方式:
NLR:前序遍历(Preorder Traversal亦称先序遍历)——访问根结点—>根的左子树—>根的右子树。LNR:中序遍历(Inorder Traversal)——根的左子树—>根节点—>根的右子树。LRN:后序遍历(Postorder Traversal)——根的左子树—>根的右子树—>根节点。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
前序遍历:先输出父节点,再遍历左子树和右子树
中序遍历:先遍历左子树,再输出父节点,再遍历右子树
后序遍历:先遍历左子树,再遍历右子树,最后输出父节点
public class BinaryTree {class TreeNode{public char val;public TreeNode left;public TreeNode right;public TreeNode(char val){this.val = val;}}//创建一个二叉树public TreeNode createTree() {TreeNode A = new TreeNode('a');TreeNode B = new TreeNode('b');TreeNode C = new TreeNode('c');TreeNode D = new TreeNode('d');TreeNode E = new TreeNode('e');TreeNode F = new TreeNode('f');TreeNode G = new TreeNode('g');TreeNode H = new TreeNode('h');A.left = B;A.right = C;B.left = D;B.right = E;E.right = H;C.left = F;C.right = G;return A;}//前序遍历void preOrderTraversal(TreeNode root){if(root == null){return;}System.out.print(root.val + " ");preOrderTraversal(root.left);preOrderTraversal(root.right);}// 中序遍历void inOrderTraversal(TreeNode root){if(root == null){return;}inOrderTraversal(root.left);System.out.print(root.val + " ");inOrderTraversal(root.right);}// 后序遍历void postOrderTraversal(TreeNode root){if(root == null){return;}postOrderTraversal(root.left);postOrderTraversal(root.right);System.out.print(root.val + " ");}public static void main(String[] args) {BinaryTree binaryTree = new BinaryTree();TreeNode root = binaryTree.createTree();System.out.println();binaryTree.preOrderTraversal(root);//前序遍历System.out.println();binaryTree.inOrderTraversal(root);// 中序遍历System.out.println();binaryTree.postOrderTraversal(root);// 后序遍历System.out.println();}
}
结果:

相关文章:

【Java】二叉树
一、树形结构 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点: 有一个特殊…...

C++学习记录——구 模板初阶
文章目录1、泛型编程和函数模板1、函数模板的实例化2、模板参数的匹配原则2、类模板1、泛型编程和函数模板 泛型编程顾名思义,泛用性很高。之前C可以用重载来对付同名函数,但还是麻烦,有一个类型的变量就得写一个类型的函数。C对此创建了库这…...

筑基五层 —— 位运算看这篇就行了
目录 一.修炼必备 二. 位运算 二.移位运算符 三.位运算综合使用 恭喜你,成功突破至筑基五层!!! 一.修炼必备 1.入门必备:VS2019社区版,下载地址:Visual Studio 较旧的下载 - 2019、2017、201…...
windows安装proget实现nuget私有包部署
下载proget 官网 下载地址 免费下载 安装proget 下载完成之后双击安装 选择ProGet 默认选择即可 也可以指定数据库,SQL Server数据库 Server服务器名;Database数据库名;User Id用户名;Password密码 Serverlocalhost;DatabaseProGet2;User Idsa;Passwordxxxx…...

SpringBoot简单集成OpenFeign
问题 在SpringBoot中简单集成Feign,不想使用Rest Temple了。 步骤 Maven <properties><spring.cloud-version>2022.0.1</spring.cloud-version></properties> <dependencyManagement><dependencies><dependency><g…...
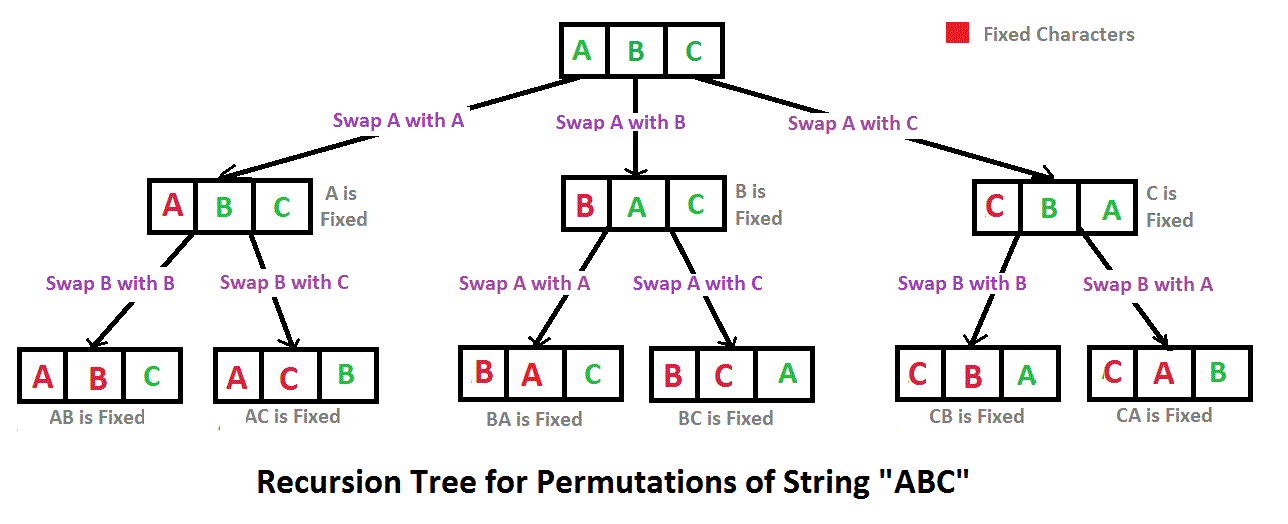
dfs(九)字符串的全排列
字符串的排列_牛客题霸_牛客网【牛客题霸】收集各企业高频校招笔面试题目,配有官方题解,在线进行百度阿里腾讯网易等互联网名企笔试面试模拟考试练习,和牛人一起讨论经典试题,全面提升你的技术能力https://www.nowcoder.com/practice/fe6b651b66ae47d7ac…...

别具一格,原创唯美浪漫情人节表白专辑,(复制就可用)(html5,css3,svg)表白爱心代码(1)
别具一格,原创唯美浪漫情人节表白专辑, (复制就可用)(html5,css3,svg)表白爱心代码(1) 一、 前言 回眸之间,丰盈了岁月,涟漪了思绪,轻轻落笔,不写伤痕,不写仇怨,只写岁月…...

Hudi-集成Spark之spark-sql方式
Hudi集成Spark之spark-sql方式 启动spark-sql # 启动spark-sql之前需要先启动Hive的Metastore nohup hive --service metastore & #针对Spark 3.2 spark-sql \--conf spark.serializerorg.apache.spark.serializer.KryoSerializer \--conf spark.sql.catalog.spark_catal…...

快速排序基本原理
快速排序基本原理1.快速排序1.1 基本原理1.2 快速排序执行步骤1.2.1 分区包含步骤1.2.1 分区步骤1.3 快速排序大O记法表示2. 将[0,5,2,1,6,3]进行快速排序 【实战】2.1 第一次分区步骤2.2 第二次分区步骤2.3 第三次分区步骤2.4 第四次分区步骤3.快速排序代码实现1.快速排序 1.…...
)
Android开发笔记-提纲(连载中....)
文章目录Android概述Android开发学习笔记提纲1. 认识AS开发Android的基础入门知识2. 认识Activity的生命周期和基础使用3. 认识Activity之间的跳转和传值4. 认识Intent以及全局Activity的属性的共享5. 认识Service6. 学习跨应用服务【AIDL通信】Android概述 Android系统框架的四…...
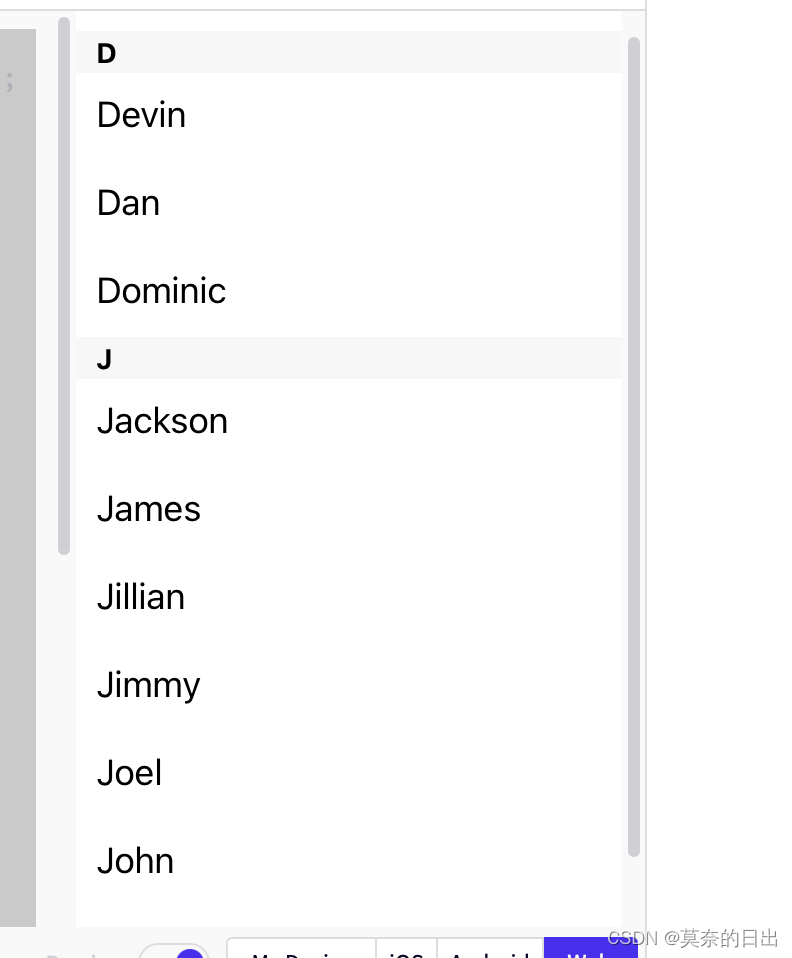
React Native(一)
移动端触摸事件example1:<ButtononPress{() > {Alert.alert(你点击了按钮!);}}title"点我!" />Touchable 系列组件TouchableHighlight 此组件的背景会在用户手指按下时变暗TouchableNativeFeedback 会在用户手指按下时形成类似墨水涟…...

Kotlin 26. Kotlin 如何播放音频文件
Kotlin 如何播放音频文件 文章目录Kotlin 如何播放音频文件1 下载并放置音频文件2 activity_main.xml3 MainActivity.kt1 下载并放置音频文件 我们可以随便下载一个音频文件,比如 alarm.mp3,需要将其放置在 /res/raw/ 路径下。 2 activity_main.xml 这…...
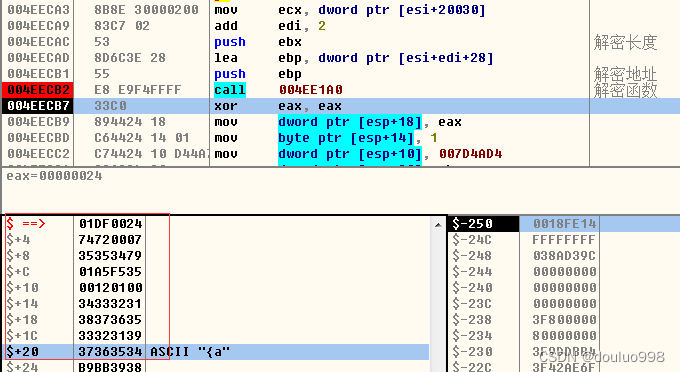
recv和明文收包分析
我们CTRLg 跳到recv 分析收包函数 发现函数会断并且收包函数返回值(收包包长)也会不断变化 那么证明recv是真正的收包函数,游戏没有重新实现该函数 我们只要分析该函数即可 在recv函数执行完毕以后下断 eax是包长,esi28是包指针 我们上2个号,让另外…...
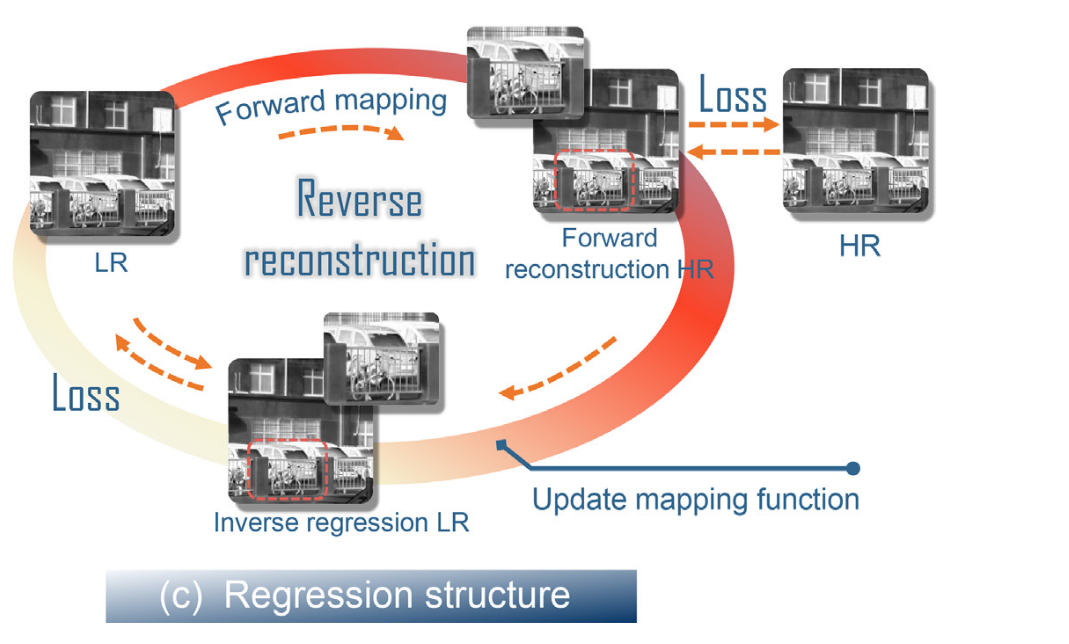
【IVIF的超分重建】
Multimodal super-resolution reconstruction of infrared and visible images via deep learning (基于深度学习的红外和可见光图像多模态超分辨率重建) 提出了一种基于编解码器结构的红外-可见光图像融合方法。图像融合任务被重新表述为保持红外-可见…...
“深度学习”学习日记。--加深网络
2023.2.13 深度学习 是加深了层的深度神经网络的学习过程。基于之前介绍的网络,只需要通过 叠加层, 就可以创建深度网络 之前的学习,已经学习到了很多东西,比如构成神经网络的各种层、参数优化方法、误差反向传播法,…...

2023前端面试总结含参考答案
文章目录1. 父子组件生命周期的执行顺序:2. 原型链:3. promise的理解:4. 数组循环,foreach,filter,map,reduce5. 数组去重,set6. 组件通信方式7. 路由钩子8. 首页首屏加载优化:9. th…...
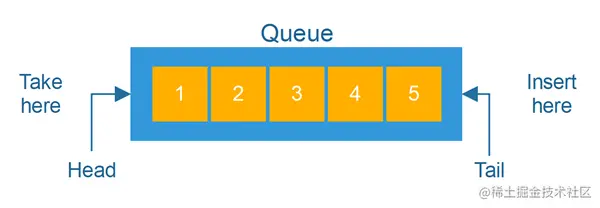
总览 Java 容器--集合框架的体系结构
前言 我们在讲 Java 的数据类型的时候,单独介绍过数组,数组也确实是开发程序中常用的内存类型之一,不过 Java 内置的数组限制颇多,所以此后扩展出了List这种结构,与之类似的Set、Queue 这些内存中的容器都被放在了 Co…...

即便考分很好也不予录取的研究生复试红线,都是原则性问题
在浙大研究生招生录取政策文件中有这么一句话:坚持“按需招生、全面衡量、择优录取、宁缺毋滥”的原则,以提高人才选拔质量为核心,在确保安全性、公平性和科学性的基础上,做到统筹兼顾、精准施策、严格管理。字字体现出研究生招生…...

Android java创建子线程的几种方法
1.新建一个类继承自Thread,并重写run()方法,并在里面编写耗时逻辑。 1 2 3 4 5 6 7 class ThreadTest extends Thread { Override public void run() { //具体的耗时逻辑代码 } } new ThreadTest().st…...
UVa 11212 Editing a Book 编辑书稿 IDA* Iterative Deepening A Star 迭代加深搜剪枝
题目链接:Editing a Book 题目描述: 给定nnn个(1<n<10)1<n<10)1<n<10)数字,数字分别是1,2,3,...,n1, 2, 3, ...,n1,2,3,...,n,但是顺序是打乱的,你可以选择一个索引区间的数字进行剪切操作。问最少进…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
