障碍感知 | 基于KD树的障碍物快速处理(附案例分析与ROS C++仿真)

1 障碍处理与KD树

在机器人感知系统中，传感器（如激光雷达、摄像头等）会采集周围的环境数据，例如代价地图、八叉树地图等，都是环境数据的表现形式。机器人在移动过程中需要根据环境，确定当前路径上的潜在障碍物。然而，这些障碍物的数量通常非常庞大，直接遍历处理往往会产生非常高的延迟，在动态环境或高实时性任务中对下游算法非常不利。

KD树（K-Dimensional tree）是一种用于高维空间数据的高效数据结构，广泛应用于机器人障碍物感知与处理中。它的主要功能是提供快速的最近邻搜索、范围查询等操作，使机器人可以实时检测到路径上的障碍物，及时调整其运动轨迹，避免碰撞。对于复杂环境中的机器人，KD树的高效查询能力尤为重要。此外，KD树可以通过增量更新来适应这些变化，而不需要重新构建整个数据结构。这样，机器人可以持续感知并适应环境的变化，保持高效的障碍物检测和避障能力。

接下来通过一个案例分析KD树的原理，并展示基于ROS的实际应用效果

2 KD树核心原理

KD树是一棵空间二叉树，其中任意节点$\mathbf{x}\in {\mathbb{R}}^k$。所有非叶子节点包含一个把空间分成两个半空间的超平面。节点的左子树组织了位于其超平面左侧的点，右子树同理。KD树不仅应用于最近邻搜索，在多维键值搜索、范围搜寻等方面也有广泛应用。

2.1 KD树的构造

KD树构造的核心是超平面的选择与划分，经典方法是随着树深度加深，轮流选择特征维度作为超平面的法向量，二分空间时只考虑样本在该维度的取值。如图所示，KD树的每个节点是二维样本，则超平面轮流以$x$、$y$轴为法向量，划分时小于根节点法向特征值的样本被划分到左子树，反之划分到右子树。

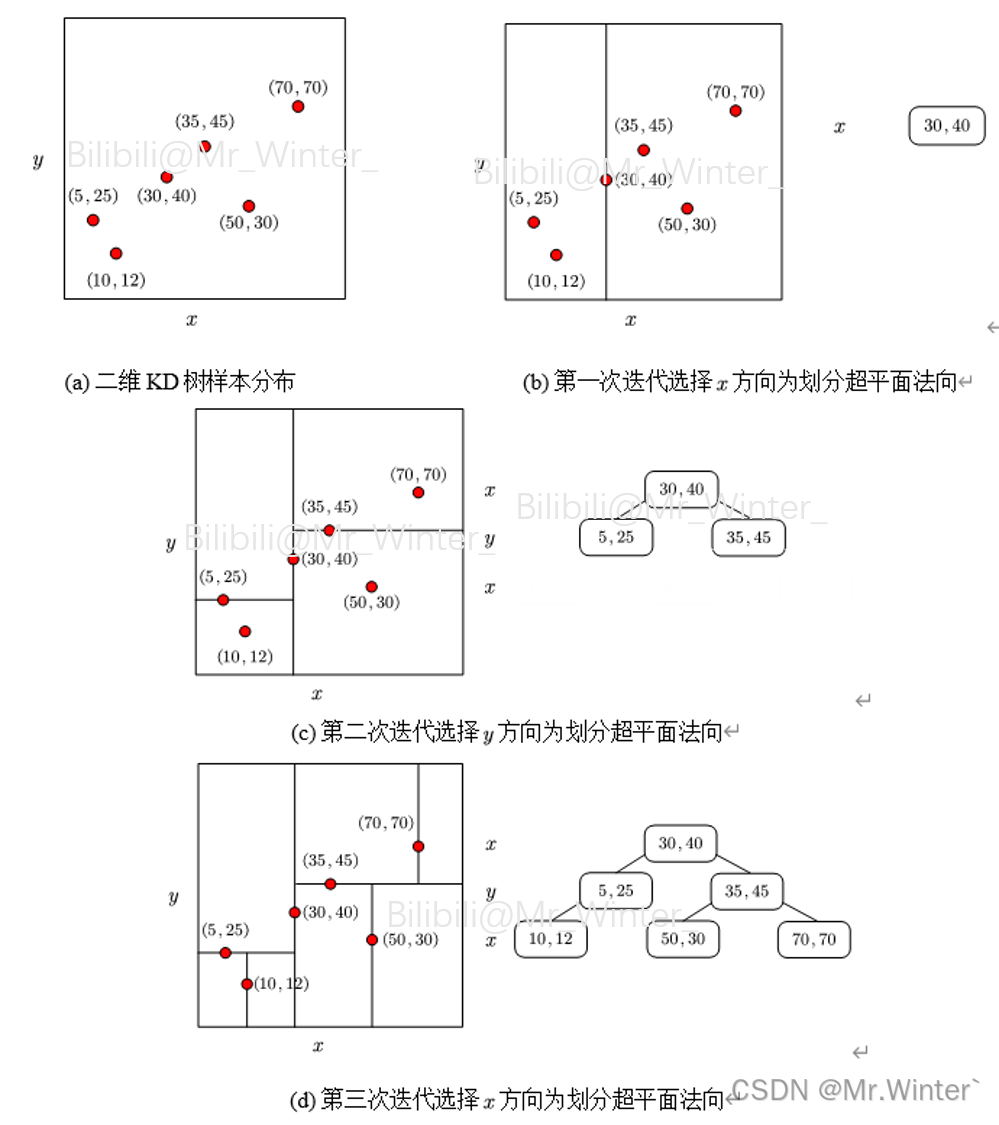
2.2 KD树的查找

KD树最近邻查找的核心是递归搜索。在一次迭代中，根据测试点与KD树当前节点相应特征维度的大小关系选择要搜索的子树并执行搜索。但是最近邻点不一定位于这个子树中，需要进行判断：每次查询测试点与KD树节点关系时，会更新一次最小距离${\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}}_{\min }$，最近邻点一定位于以测试点为圆心、${\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}}_{\min }$为半径的圆内；计算相应特征维距离${\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}}_{\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s}}$，若${\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}}_{\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s}}<{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}}_{\min }$，说明当前KD树节点包含的超平面穿过了最近邻圆域，则该节点的另一子树也需要递归搜索

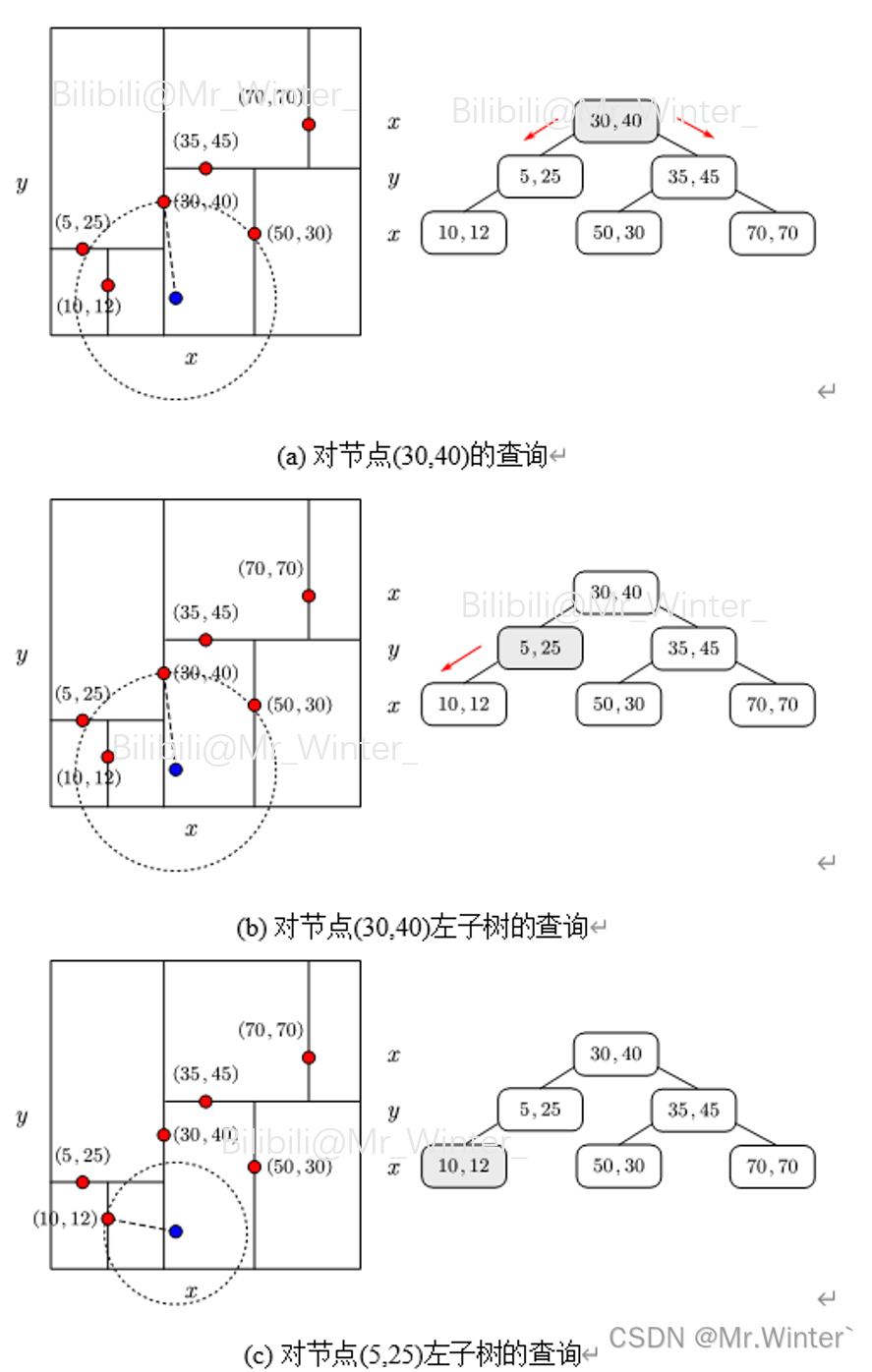
如图所示为KD树最近邻查找的实例。

如图(a)所示，第一次查找节点(30,40)并更新最近邻圆，由于测试点位于节点(30,40)右侧，因此需要继续查询右子树；同时最近邻圆被节点(30,40)包含的超平面$x=30$穿过，所以节点(30,40)的左侧也可能包含最近邻点，故左子树也被查询。

如图(b)所示是下一层递归时对节点(30,40)左子树根节点(5,25)的查询，由于测试点位于节点(5,25)下侧，因此需要继续查询左子树；此时最近邻圆没有更新，被节点(5,25)包含的超平面$y=25$穿过，所以节点(5,25)的上侧也可能包含最近邻点，但节点(5,25)不存在右子树，故其右子树查询退出递归。

如图(c)所示是下一层递归时对节点(5,25)左子树根节点(10,12)的查询，考虑到是叶节点，直接更新最近邻圆即可。

在节点(30,40)右子树的查询中，首先进入节点(35,45)，类似地应查询其左子树，但节点(35,45)包含的超平面$y=45$没穿过最近邻圆，说明节点(35,45)右子树的所有点都在最近邻圆外部，不可能是最近邻点，可以进行剪枝，提高计算效率。

3 仿真实现

3.1 KD树基本算法

KD树的查找主要分为以下三种模式

• 最近邻查找

  int nnSearch(const PointT& query, double* min_dist = nullptr) const
  {int guess;double _min_dist = std::numeric_limits<double>::max();_nnSearchRecursive(query, root_, &guess, &_min_dist);if (min_dist)*min_dist = _min_dist;return guess;
  }void _nnSearchRecursive(const PointT& query, const KDNode* node, int* guess, double* min_dist) const
  {if (node == nullptr)return;const PointT& train = points_[node->idx];const double dist = _distance(query, train);if (dist < *min_dist){*min_dist = dist;*guess = node->idx;}const int axis = node->axis;const int dir = query[axis] < train[axis] ? 0 : 1;_nnSearchRecursive(query, node->next[dir], guess, min_dist);// if the min distance crosses the axis, the nearest neighbor maybe exist// in the other side of axis, therefore another direction should be searchedconst double diff = fabs(query[axis] - train[axis]);if (diff < *min_dist)_nnSearchRecursive(query, node->next[!dir], guess, min_dist);
  }
  

• K近邻查找

  std::vector<int> knnSearch(const PointT& query, int k) const
  {KnnQueue queue(k);_knnSearchRecursive(query, root_, queue, k);std::vector<int> indices(queue.size());for (size_t i = 0; i < queue.size(); i++)indices[i] = queue[i].second;return indices;
  }void _knnSearchRecursive(const PointT& query, const KDNode* node, KnnQueue& queue, int k) const
  {if (node == nullptr)return;const PointT& train = points_[node->idx];const double dist = _distance(query, train);queue.push(std::make_pair(dist, node->idx));const int axis = node->axis;const int dir = query[axis] < train[axis] ? 0 : 1;_knnSearchRecursive(query, node->next[dir], queue, k);const double diff = fabs(query[axis] - train[axis]);if ((int)queue.size() < k || diff < queue.back().first)_knnSearchRecursive(query, node->next[!dir], queue, k);
  }
  

• 圆形近邻查找

  std::vector<int> radiusSearch(const PointT& query, double radius) const
  {std::vector<int> indices;_radiusSearchRecursive(query, root_, indices, radius);return indices;
  }void _radiusSearchRecursive(const PointT& query, const KDNode* node, std::vector<int>& indices, double radius) const
  {if (node == nullptr)return;const PointT& train = points_[node->idx];const double dist = _distance(query, train);if (dist < radius)indices.push_back(node->idx);const int axis = node->axis;const int dir = query[axis] < train[axis] ? 0 : 1;_radiusSearchRecursive(query, node->next[dir], indices, radius);const double diff = fabs(query[axis] - train[axis]);if (diff < radius)_radiusSearchRecursive(query, node->next[!dir], indices, radius);
  }
  

3.2 ROS C++仿真

首先在主节点中构造KD树对象，并将代价地图的障碍信息传入KD树

rmp::common::structure::KDTree<rmp::common::geometry::Point3d> obs_kd_tree;
rmp::common::geometry::Points3d obstacles;
auto grid2Index = [&](int x, int y) { return x + costmap_ros_->getCostmap()->getSizeInCellsX() * y; };
for (int x = 0; x < costmap_ros_->getCostmap()->getSizeInCellsX(); x++)
{for (int y = 0; y < costmap_ros_->getCostmap()->getSizeInCellsY(); y++){if (costmap_ros_->getCostmap()->getCharMap()[grid2Index(x, y)] == costmap_2d::INSCRIBED_INFLATED_OBSTACLE){double wx, wy;costmap_ros_->getCostmap()->mapToWorld(x, y, wx, wy);obstacles.emplace_back(wx, wy);}}
}obs_kd_tree.build(obstacles);
rmp::common::geometry::Point3d robot_pose(start.pose.position.x, start.pose.position.y, start.pose.position.z);

接着测试不同的KD树障碍物搜索算法

• 最近邻查找

  auto idx = obs_kd_tree.nnSearch(robot_pose);
  Visualizer::Lines2d knn;
  knn.emplace_back(std::make_pair<Visualizer::Point2d, Visualizer::Point2d>({ start.pose.position.x, start.pose.position.y }, { obs_kd_tree[idx].x(), obs_kd_tree[idx].y() }));
  visualizer->publishLines2d(knn, particles_pub_, frame_id_, "knn", Visualizer::PURPLE, 0.1);
  

  

• K近邻查找

  auto obs_idx = obs_kd_tree.knnSearch(robot_pose, 10);
  Visualizer::Lines2d knn;
  for (const int idx : obs_idx)
  {knn.emplace_back(std::make_pair<Visualizer::Point2d, Visualizer::Point2d>({ start.pose.position.x, start.pose.position.y }, { obs_kd_tree[idx].x(), obs_kd_tree[idx].y() }));
  }
  visualizer->publishLines2d(knn, particles_pub_, frame_id_, "knn", Visualizer::PURPLE, 0.1);
  

• 圆形近邻查找

  auto obs_idx = obs_kd_tree.radiusSearch(robot_pose, 2.0);
  Visualizer::Lines2d knn;
  for (const int idx : obs_idx)
  {knn.emplace_back(std::make_pair<Visualizer::Point2d, Visualizer::Point2d>({ start.pose.position.x, start.pose.position.y }, { obs_kd_tree[idx].x(), obs_kd_tree[idx].y() }));
  }
  visualizer->publishLines2d(knn, particles_pub_, frame_id_, "knn", Visualizer::PURPLE, 0.1);
  

  

完整工程代码请联系下方博主名片获取

---

🔥 更多精彩专栏：

• 《ROS从入门到精通》
• 《Pytorch深度学习实战》
• 《机器学习强基计划》
• 《运动规划实战精讲》
• …

👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇