二分查找题目:两球之间的磁力
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:两球之间的磁力
出处:1552. 两球之间的磁力
难度
5 级
题目描述
要求
在代号为地球 C-137 的世界中,Rick 发现如果他将两个球放在他新发明的篮子中,它们之间会形成特殊形式的磁力。Rick 有 n \texttt{n} n 个空的篮子,第 i \texttt{i} i 个篮子的位置在 position[i] \texttt{position[i]} position[i],Morty 想把 m \texttt{m} m 个球放到这些篮子中,使得任意两球间的最小磁力最大。
Rick 声明,两个位于 x \texttt{x} x 和 y \texttt{y} y 的球之间的磁力为 |x - y| \texttt{|x - y|} |x - y|。
给定一个整数数组 position \texttt{position} position 和一个整数 m \texttt{m} m,返回最小磁力的最大值。
示例
示例 1:
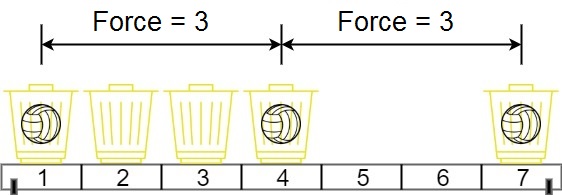
输入: position = [1,2,3,4,7], m = 3 \texttt{position = [1,2,3,4,7], m = 3} position = [1,2,3,4,7], m = 3
输出: 3 \texttt{3} 3
解释:将 3 \texttt{3} 3 个球分别放入位于 1 \texttt{1} 1、 4 \texttt{4} 4 和 7 \texttt{7} 7 的三个篮子,两球间的磁力分别为 [3, 3, 6] \texttt{[3, 3, 6]} [3, 3, 6]。最小磁力为 3 \texttt{3} 3。我们无法让最小磁力大于 3 \texttt{3} 3。
示例 2:
输入: position = [5,4,3,2,1,1000000000], m = 2 \texttt{position = [5,4,3,2,1,1000000000], m = 2} position = [5,4,3,2,1,1000000000], m = 2
输出: 999999999 \texttt{999999999} 999999999
解释:我们使用位于 1 \texttt{1} 1 和 1000000000 \texttt{1000000000} 1000000000 的篮子时最小磁力最大。
数据范围
- n = position.length \texttt{n} = \texttt{position.length} n=position.length
- 2 ≤ n ≤ 10 5 \texttt{2} \le \texttt{n} \le \texttt{10}^\texttt{5} 2≤n≤105
- 1 ≤ position[i] ≤ 10 9 \texttt{1} \le \texttt{position[i]} \le \texttt{10}^\texttt{9} 1≤position[i]≤109
- 所有 position \texttt{position} position 中的整数各不相同
- 2 ≤ m ≤ position.length \texttt{2} \le \texttt{m} \le \texttt{position.length} 2≤m≤position.length
解法
思路和算法
由于两个球之间的磁力等于两个球之间的距离,因此为了得到最小磁力,需要计算最小距离。以下将最小磁力的最大值对应的最小距离的最大值称为「临界距离」。
当 m m m 个球已经放入篮子时,最小距离一定是其中一对位置相邻的球之间的距离,因此需要将数组 position \textit{position} position 升序排序,在排序后的篮子位置之间计算放入的球的最小距离。
如果任意两个球之间的距离不超过临界距离,则可以放入至少 m m m 个球;如果存在两个球之间的距离大于临界距离,则不能放入 m m m 个球。因此,这道题是二分查找判定问题,需要找到可以放入 m m m 个球的最小距离的最大值。
用 low \textit{low} low 和 high \textit{high} high 分别表示二分查找的下界和上界。由于至少需要放入两个球,当最小距离最大时每个球放在不同的篮子中,因此 low \textit{low} low 的初始值等于 1 1 1;由于最大距离为两端的篮子之间的距离,因此 high \textit{high} high 的初始值等于 position \textit{position} position 中的最大值与最小值之差。
为了能放入 m m m 个球,当最小距离确定时,应该在确保相邻的球之间的距离不小于最小距离的前提下尽可能放入更多的球。因此,第一个球应该放到最左边的篮子中,后面的每个球应该放到与前一个球的距离大于等于最小距离的最近的篮子中。根据该规则,遍历排序后的数组 position \textit{position} position,判断每个球应该放到哪些篮子中,并计算放到篮子中的球的总数。
每次查找时,取 mid \textit{mid} mid 为 low \textit{low} low 和 high \textit{high} high 的平均数向上取整,将 mid \textit{mid} mid 作为最小距离,判断是否可以将 m m m 个球放到篮子中,执行如下操作。
-
如果最小距离是 mid \textit{mid} mid 时可以将 m m m 个球放到篮子中,则临界距离大于等于 mid \textit{mid} mid,因此在 [ mid , high ] [\textit{mid}, \textit{high}] [mid,high] 中继续查找。
-
如果最小距离是 mid \textit{mid} mid 时不能将 m m m 个球放到篮子中,则临界距离小于 mid \textit{mid} mid,因此在 [ low , mid − 1 ] [\textit{low}, \textit{mid} - 1] [low,mid−1] 中继续查找。
当 low = high \textit{low} = \textit{high} low=high 时,查找结束,此时 low \textit{low} low 即为临界距离。
得到临界距离之后,临界距离对应的磁力即为最小磁力的最大值。
代码
class Solution {public int maxDistance(int[] position, int m) {Arrays.sort(position);int n = position.length;int low = 1, high = position[n - 1] - position[0];while (low < high) {int mid = low + (high - low + 1) / 2;if (canPutMBalls(position, m, mid)) {low = mid;} else {high = mid - 1;}}return low;}public boolean canPutMBalls(int[] position, int m, int force) {int count = 1;int prev = position[0];int n = position.length;for (int i = 1; i < n; i++) {if (position[i] - prev >= force) {count++;if (count == m) {return true;}prev = position[i];}}return false;}
}
复杂度分析
-
时间复杂度: O ( n log ( n p ) ) O(n \log (np)) O(nlog(np)),其中 n n n 是数组 position \textit{position} position 的长度, p p p 是数组 position \textit{position} position 中的最大值。排序需要 O ( n log n ) O(n \log n) O(nlogn) 的时间,排序之后需要执行 O ( log p ) O(\log p) O(logp) 次二分查找,每次二分查找需要 O ( n ) O(n) O(n) 的时间遍历数组 position \textit{position} position 判断是否可以将 m m m 个球放到篮子中,二分查找共需要 O ( n log p ) O(n \log p) O(nlogp) 的时间,因此时间复杂度是 O ( n log n + n log p ) = O ( n log ( n p ) ) O(n \log n + n \log p) = O(n \log (np)) O(nlogn+nlogp)=O(nlog(np))。
-
空间复杂度: O ( log n ) O(\log n) O(logn),其中 n n n 是数组 position \textit{position} position 的长度。排序需要 O ( log n ) O(\log n) O(logn) 的递归调用栈空间。
相关文章:

二分查找题目:两球之间的磁力
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法思路和算法代码复杂度分析 题目 标题和出处 标题:两球之间的磁力 出处:1552. 两球之间的磁力 难度 5 级 题目描述 要求 在代号为地球 C-137 的世界中,Rick 发现如果他将两个…...
估计两个三维点集之间的最优平移变换函数estimateTranslation3D()的使用)
OpenCV相机标定与3D重建(28)估计两个三维点集之间的最优平移变换函数estimateTranslation3D()的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 计算两个3D点集之间的最优平移。 它计算 [ x y z ] [ X Y Z ] [ b 1 b 2 b 3 ] \begin{bmatrix} x\\ y\\ z\\ \end{bmatrix} \begin{bmatri…...

UE5仿漫威争锋灵蝶冲刺技能
这两天玩了一下漫威争锋Marvel Rivals,发现是UE5做的,对里面一些角色技能挺感兴趣的,想简单复刻一下技能功能,顺便复习一下学过的知识 首先把摄像机设置调整一下 CameraBoom里搜索lag 把摄像机延迟关掉 ,这样摄像机就…...

CSS盒子模型(溢出隐藏,块级元素和行级元素的居中对齐,元素样式重置)
overflow:值 规定了内容溢出元素框时所发生的事情 visible:内容不会被修剪,会显示在元素框之外,默认值 overflow: visible; hidden:内容会被修剪,溢出内容不可见 overflow: hidden; scroll:内…...

语音增强的损失函数选择
一、最优尺度不变信噪比(OSISNR)损失函数 参考:论文解读 --Optimal scale-invariant signal-to-noise ratio and curriculum learning for monaural multi-spea 最优尺度不变信噪比(OSI-SNR)是一种用于评估信号质量…...
【python自动化六】UI自动化基础-selenium的使用
selenium是目前用得比较多的UI自动化测试框架,支持java,python等多种语言,目前我们就选用selenium来做UI自动化。 1.selenium安装 安装命令 pip install selenium2.selenium的简单使用 本文以chrome浏览器为例,配套selenium中c…...

【习题答案】让您的应用拥有领先的位置服务能力
判断题 1.在使用(逆)地理编码前,需要使用isGeocoderAvailable检查服务状态。 正确(True) 错误(False) 2.当同时配置定位场景和优先级策略时,会优先使用优先级策略。 正确(True) 错误(False) 单选题 1.获取精准定位需要申请哪个权…...

java中list和map区别
在Java中,List和Map是两种不同类型的集合接口,它们用于不同的场景并且具有不同的特性和用途。以下是List和Map的主要区别: 1. 数据结构 List:是一个有序的集合,允许重复元素。它实现了Collection接口,并且…...

java后端传时间戳给前端的三种方式
一. 后端传时间戳给前端的几种方式 使用System.currentTimeMillis() 这是最简单的方式,返回自1970年1月1日(UTC)以来的毫秒数,可以直接传递给前端。 long timestamp1 System.currentTimeMillis();使用java.time.Instant Java…...

【机器学习与数据挖掘实战】案例06:基于Apriori算法的餐饮企业菜品关联分析
【作者主页】Francek Chen 【专栏介绍】 ⌈ ⌈ ⌈机器学习与数据挖掘实战 ⌋ ⌋ ⌋ 机器学习是人工智能的一个分支,专注于让计算机系统通过数据学习和改进。它利用统计和计算方法,使模型能够从数据中自动提取特征并做出预测或决策。数据挖掘则是从大型数据集中发现模式、关联…...

oracle: create new database
用database configuration Assistant 引导创建数据库。记得给system,sys 设置自己的口令,便于添加新操作用户。 创建操作用户: -- 别加双引号,否则,无法用 create user geovindu identified by 888888; create user geovin identi…...

混合开发环境---使用编程AI辅助开发Qt
文章目录 [toc]1、说明2、演示视频 1、说明 新时代的浪潮早就已经来临,上不了船的人终将被抛弃,合理使用AI辅助开发、提升效率是大趋势 注意:不要被AI奴隶 合理使用AI辅助编程,十倍提升效率。 大部分的编程AI都有vs code插件&…...

Sigrity SystemSI仿真分析教程文件路径
为了方便读者能够快速上手和学会Sigrity SystemSI 的功能,将Sigrity SystemSI仿真分析教程专栏所有文章对应的实例文件上传至以下路径 https://download.csdn.net/download/weixin_54787054/90171488?spm1001.2014.3001.5503...

【YashanDB知识库】Oracle pipelined函数在YashanDB中的改写
本文内容来自YashanDB官网,原文内容请见 https://www.yashandb.com/newsinfo/7802940.html?templateId1718516 【问题分类】功能使用 【关键字】pipelined 【问题描述】 Oracle PL/SQL中包含pipelined函数的对象迁移到YashanDB会出现不兼容现象。 【问题原因分…...
【开发实战】QT5+ 工业相机 + OpenCV工作流集成演示
学习《OpenCV应用开发:入门、进阶与工程化实践》一书 做真正的OpenCV开发者,从入门到入职,一步到位! 概述 基于OpenCV工作流引擎SDK Qt5 海康工业相机实现了从图像采集到OpenCV工作流运行的完整流程。其中工业相机采图是一个单…...
各种电机原理介绍
1,直流电机 (1)基本原理 直流电动机由直流电驱动电池或外部电源为其供电。在最简单的直流电动机中,定子为永磁体(即红蓝磁体外壳),转子是一个电磁体(即线圈),电流通过碳刷和一个换向器作用于转动的线圈。…...

深入了解 React:从入门到高级应用
深入了解 React:从入门到高级应用 React 是由 Facebook 开发并维护的一个开源 JavaScript 库,用于构建用户界面。自2013年发布以来,React 在前端开发领域迅速崛起,成为最受欢迎的 UI 构建工具之一。无论是小型的单页应用…...

Cglib代理简单案例
Cglib代理简单案例 前言: 1,实现对目标类的增强 2,源码后期补齐 步骤 1,添加cglib依赖 2,编写目标类,书写里面的方法 3,实现MethodInterceptor 接口,重写intercept方法 4ÿ…...

FreeMarker语法
1. 查找转移 <#function getSubSlot x > <#return (x) ? switch( "1", "L", "2", "R", "" )> </#function> 2. 转换数字 ?number ${mergedMap[placement.sequence].material.subs…...
)
DP动态规划(装箱问题)
# [NOIP2001 普及组] 装箱问题 ## 题目描述 有一个箱子容量为 $V$,同时有 $n$ 个物品,每个物品有一个体积。 现在从 $n$ 个物品中,任取若干个装入箱内(也可以不取),使箱子的剩余空间最小。输出这个最小值。…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
