编译原理复习---正则表达式+有穷自动机
适用于电子科技大学编译原理期末考试复习。
1. 正则表达式
正则表达式(Regular Expression,简称regex或regexp)是一种用于描述、匹配和操作文本模式的强大工具。它由一系列字符和特殊符号组成,这些字符和符号定义了一种搜索模式,可以用来检查一个字符串是否包含某个子串、将匹配的子串进行替换或者从字符串中提取符合条件的子串等。
总结来说,正则表达式就是通过特定字符与文法符号的组合来描述一种语言的方式。
正则语言 == 上下文无关文法 == 正则表达式,三者之间可以相互转换
编译原理这门课中,正则表达式所使用的符号与标准的定义好像不太相同,我只能凭借做题的经验列举出大致的用法:
:表示集合{
,
,...,
}中的任意一个字符。
每一个单元(正则表达式中的一个字符或用括号包围起来的一组符号)后可加上" * "(克林闭包)、" + "(正闭包)。
" . "表示字母表中的任意字符。
例如:
2. 有穷自动机
有穷自动机(Finite Automaton, FA),也称为有限状态机,是一种计算模型,用于描述和识别特定类型的语言。它由以下几个基本组成部分构成:
状态集合(Q):有限个状态的集合。
字母表(Σ):有限个输入符号的集合。
转移函数(δ):定义了从一个状态和一个输入符号到另一个状态的映射,即 δ: Q × Σ → Q。
初始状态(q0):自动机开始处理输入前所在的状态,q0 ∈ Q。
接受状态集(F):状态集合的一个子集,表示当自动机停止时可以处于的状态,这些状态表明输入字符串被接受,F ⊆ Q。
通常,我们使用状态转换图来表示有穷自动机:

有穷自动机可以分为确定型有穷自动机(Deterministic Finite Automaton, DFA)和非确定型有穷自动机(Nondeterministic Finite Automaton, NFA)。
DFA的每一步操作都是确定的,即对于一个状态和一个输入符号,有唯一确定的下一个状态。

而NFA在某些状态下,对于一个输入符号可能有多个可能的下一个状态。
相对于DFA,NFA更加直观,但是对于计算机来说,DFA才方便其使用。
我们要将正则表达式转换为DFA并不好转换,可以先将其转换为更加直观的NFA,然后再将NFA转换为DFA。
3. 正则表达式转换为NFA
3.1 单个符号的NFA

3.2 (a|b)的NFA,并联
 3.3 ab的NFA,串联
3.3 ab的NFA,串联

3.4 a*的NFA
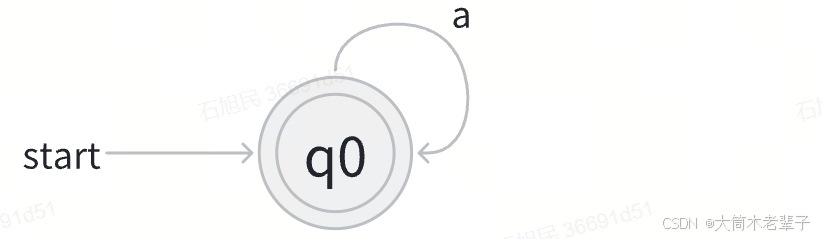
通过以上四种方式,我们可以逐步将一个正则表达式转换为NFA。
4. NFA转化为DFA
初始状态在遇到某个输入符号时能进入的所有状态的集合定义为一个新的状态,在DFA的状态图中,初始状态指向该新状态。
对每个输入符号都进行检查,定义出一系列新的状态。
对于每个新状态,将其当作初始状态并重复上面两步,直到不再有新状态产生。
注意,当通过某个输入符号到达某一状态时,新到达的状态如果可以通过空边到达其他状态,那么也视为在遇到该输入符号时能到达这些状态。
如果初始状态可以通过空边到达其他状态,那么应该把这几个状态连同初始状态当作DFA中的初始状态。
举例子太费劲了,就不举了。
相关文章:

编译原理复习---正则表达式+有穷自动机
适用于电子科技大学编译原理期末考试复习。 1. 正则表达式 正则表达式(Regular Expression,简称regex或regexp)是一种用于描述、匹配和操作文本模式的强大工具。它由一系列字符和特殊符号组成,这些字符和符号定义了一种搜索模式…...
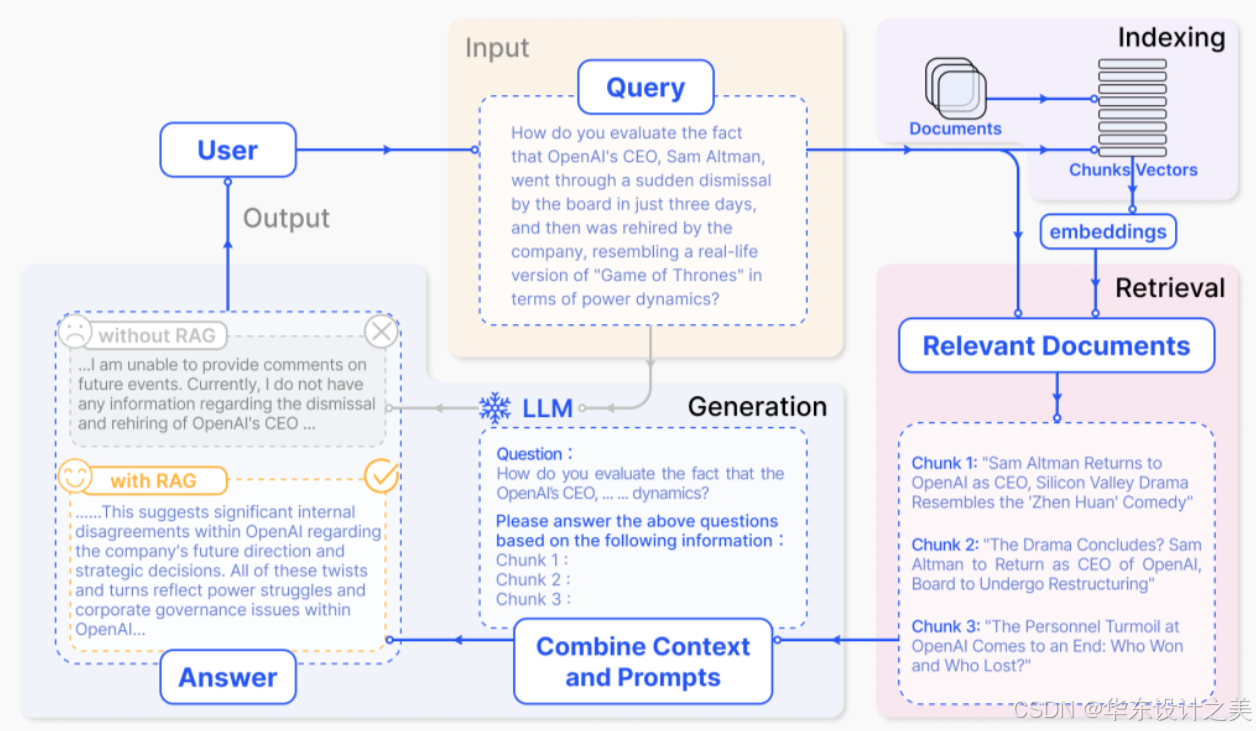
知识图谱+RAG学习
GraphRAG(Graph-based Retrieval-Augmented Generation)是微软在2024年推出的一项开源技术,旨在通过结合知识图谱和检索增强生成(RAG)方法,为大型语言模型(LLM)的数据处理提供全新解…...
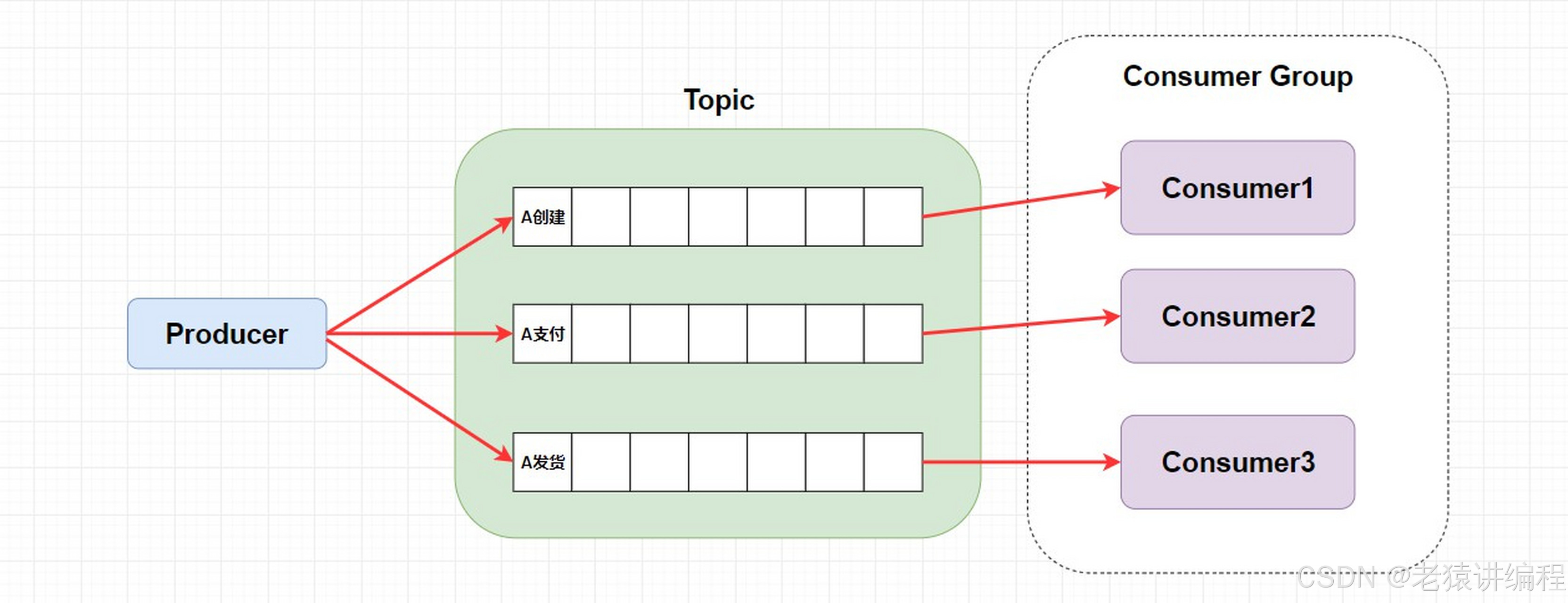
消息队列技术的发展历史
消息队列技术的演进历程宛如一幅波澜壮阔的科技画卷,历经多个标志性阶段,各阶段紧密贴合不同的技术需求与市场风向,下面为您详细道来。 第一阶段:消息中间件的起源(1970 年代末期 - 1980 年代中期) 在计算…...

每天40分玩转Django:Django部署
Django部署 一、今日学习内容概述 学习模块重要程度主要内容生产环境配置⭐⭐⭐⭐⭐settings配置、环境变量WSGI服务器⭐⭐⭐⭐⭐Gunicorn配置、性能优化Nginx配置⭐⭐⭐⭐反向代理、静态文件安全设置⭐⭐⭐⭐⭐SSL证书、安全选项 二、生产环境配置 2.1 项目结构调整 mypr…...
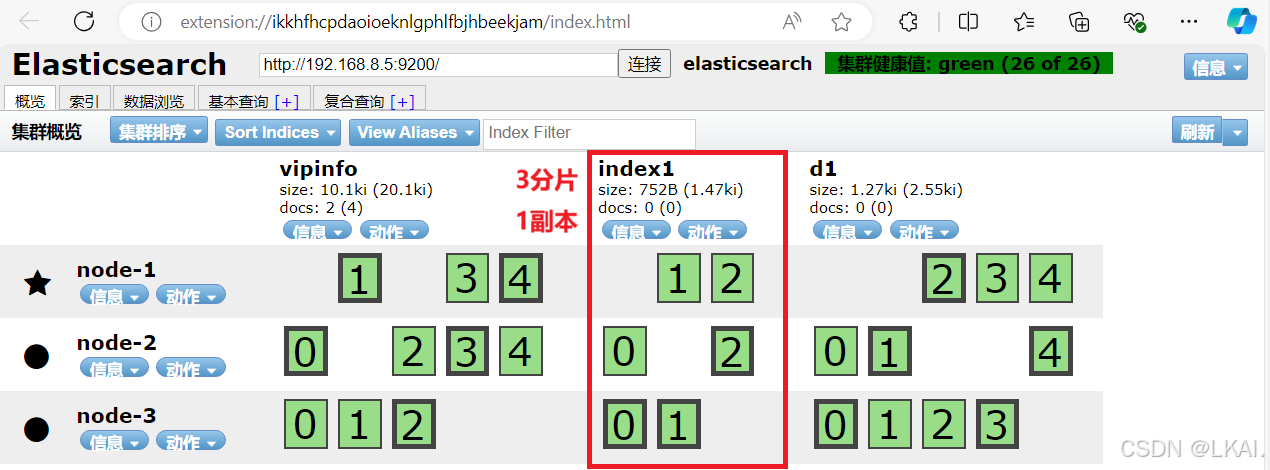
搭建Elastic search群集
一、实验环境 二、实验步骤 Elasticsearch 是一个分布式、高扩展、高实时的搜索与数据分析引擎Elasticsearch目录文件: /etc/elasticsearch/elasticsearch.yml#配置文件 /etc/elasticsearch/jvm.options#java虚拟机 /etc/init.d/elasticsearch#服务启动脚本 /e…...
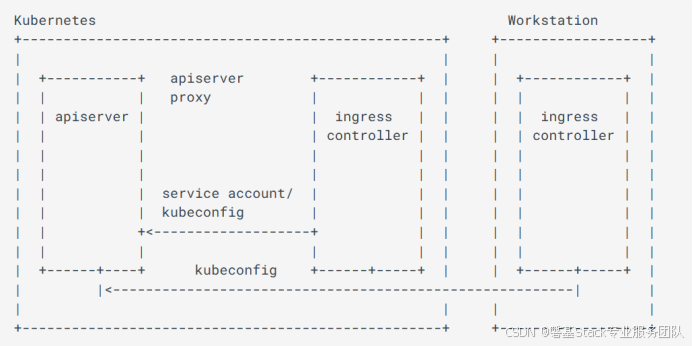
解析 Ingress-Nginx 故障:排查思路与方法
文章目录 一、什么是Ingress-Nginx二、故障排除1.1Ingress-Controller日志和事件检查 Ingress 资源事件检查 Nginx 配置检查使用的服务是否存在调试日志 1.2对 Kubernetes API 服务器的认证服务认证服务账户Kube-Config 1.3使用GDB和Nginx1.4在 Nginx 4.2.5 或其他版本…...

2024 楚慧杯 re wp
go_bytes 附件拖入ida 输入长度为0x28,每两位字符的4bit拼接 与一个常量值经过运算后的值进行异或,并且判断是否相等 脚本 bouquet 附件拖入ida。简单去一下花 构建了一个二叉树,然后递归调用函数 重新排列一下再层序遍历读出即可 zistel 附件…...

【物联网技术与应用】实验10:蜂鸣器实验
实验10 蜂鸣器实验 【实验介绍】 蜂鸣器是音频信号装置。蜂鸣器可分为有源蜂鸣器和无源蜂鸣器。 【实验组件】 ● Arduino Uno主板* 1 ● USB数据线* 1 ● 有源蜂鸣器* 1 ● 无源蜂鸣器* 1 ● 面包板* 1 ● 9V方型电池* 1 ● 跳线若干 【实验原理】 如图所示&#x…...
)
单片机:实现矩阵键盘控制LCD屏幕(附带源码)
单片机实现矩阵键盘控制LCD屏幕 矩阵键盘(Matrix Keypad)是一种常用的输入设备,广泛应用于嵌入式系统中。在许多嵌入式应用中,我们常常需要通过按键输入来控制系统的功能。结合LCD显示屏,我们可以实现一个简单的界面&…...

鸿蒙Next之包体积极限优化
鸿蒙应用包大小优化全解析 在鸿蒙应用开发中,减小应用包大小对于提升应用下载和安装体验起着关键作用。通过压缩、精简或复用应用中的代码与资源,能有效降低包体积,减少空间占用并加快下载与安装速度。下面详细介绍一下鸿蒙应用包大小优化的…...

Android实战经验篇-log工具
详细代码实现及系列文章请转如下链接 Android实战经验篇-系列文章汇总 Android Display Graphics系列文章-汇总 一、基础知识 1.1 Logging简述 我们写的第一个计算机C程序一般是printf(“Hello world!”);这就是一个log输出。Linux内核有Kernel log以及配套的Log工具&#x…...

DPU编程技术解析与实践应用
一、引言 1.1 研究背景与目的 随着信息技术的飞速发展,数据中心在现代社会中的地位日益凸显,成为支撑各行业数字化转型的关键基础设施。在数据中心内部,数据的处理速度、效率和安全性成为了影响整体性能的核心要素。为了应对不断增长的数据…...
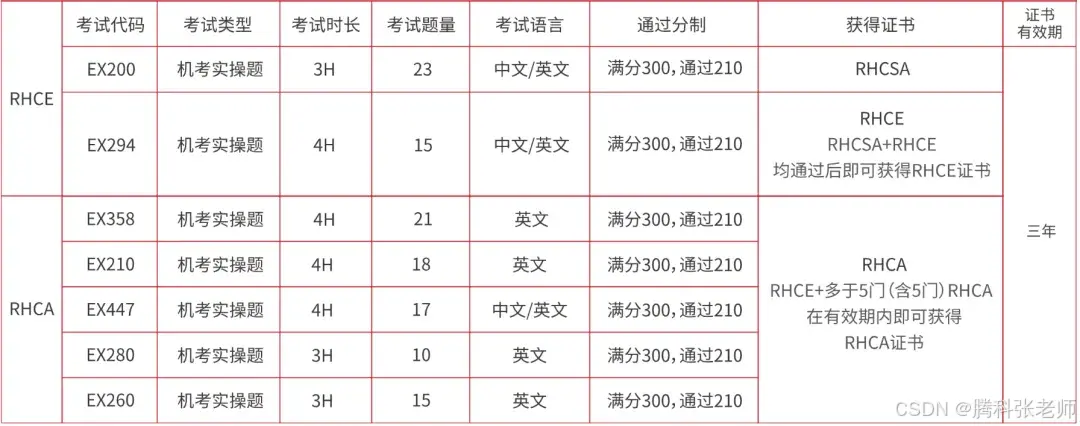
红帽认证的含金量和价值如何?怎么报名红帽认证考试?
红帽企业 Linux(RHEL)是由红帽公司提供的一款商业支持、专为生产环境设计的Linux发行版。随着IT系统和工作负载日益复杂化,底层基础设施及操作系统必须兼具可靠性、可扩展性,并能有效促进性能提升。红帽认证在全球范围享有盛誉&am…...

VS Code Copilot 与 Cursor 对比
选手简介 VS Code Copilot:算是“老牌”编程助手了,虽然Copilot在别的编辑器上也有扩展,不过体验最好的还是VS Code,毕竟都是微软家的所以功能集成更好一些;主要提供的是Complete和Chat能力,也就是代码补全…...

蓝桥杯嵌入式备赛教程(1、led,2、lcd,3、key)
一、工程模版创建流程 第一步 创建新项目 第二步 选择型号和管脚封装 第三步 RCC使能 外部时钟,高速外部时钟 第四步晶振时钟配置 由数据手册7.1可知外部晶振频率为24MHz 最后一项设置为80 按下回车他会自动配置时钟 第五步,如果不勾选可能程序只会…...

取多个集合的交集
1.我们取多个集合的交集,先把各个集合放入list中 List < Set < String > > listnew ArrayList<>();HashSet<String> set1new HashSet<>();set1.add( "A" );set1.add("B" );set1.add("C" );HashSet<…...

如何实现电子发票XML文件的合规性存档?
随着国家税务改革的推进,企业对电子发票的管理和存档要求越来越高。尤其是《财政部 国家税务总局关于进一步深化增值税发票管理改革的通知》(财会〔2023〕18号文)的发布,明确规定了电子发票的存档要求。这为企业在财务管理中的电子…...

IOT、MES、WMS、MOM 和 EPMS 系统综合技术与业务文档
IOT、MES、WMS、MOM 和 EPMS 系统综合技术与业务文档 一、引言 在现代制造业和工业管理领域,IOT(物联网)、MES(制造执行系统)、WMS(仓库管理系统)、MOM(制造运营管理系统ÿ…...

IntelliJ IDEA Docker集成
一、概述 Docker是一种用于在隔离和可复制环境中部署和运行可执行文件的工具。这可能很有用,例如,在与生产相同的环境中测试代码。 IntelliJ IDEA集成了Docker功能,并为创建Docker映像、运行Docker容器、管理Docker Compose应用程序、使用公…...

【react项目】从零搭建react项目[nodejs安装]
〇、模板git下载地址 下载即用的模板地址: http:https://e.coding.net/uijiio/init_app/react_init_app.git ssh:gite.coding.net:uijiio/init_app/react_init_app.git 目前更新至:登录与主页跳转,主页包含菜单和容器区 一、搭建基础空白React项目 1.准备…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...
