n阶Legendre多项式正交性的证明
前言
在《n次Legendre(勒让德)多项式在区间(-1, 1)上根的分布及证明》这篇文章中,我们阐述了Legendre多项式在 [ − 1 , 1 ] [-1,1] [−1,1]上的根分布情况并给出了证明。本文将证明Legendre多项式在 [ − 1 , 1 ] [-1,1] [−1,1]上的正交性质。
正交多项式的定义
设 f n ( x ) , n ∈ N f_n(x),n\in \mathbb N fn(x),n∈N是定义在 [ a , b ] [a,b] [a,b]上的一列函数,若对于任意的自然数 m , n m,n m,n, f m ( x ) f n ( x ) f_m(x)f_n(x) fm(x)fn(x)在 [ a , b ] [a,b] [a,b]上可积,且满足:
∫ a b f m ( x ) f n ( x ) d x = { 0 , m ≠ n ∫ a b f n 2 ( x ) d x > 0 , m = n \int_{a}^{b}f_m(x)f_n(x) \mathrm{d}x=\begin{cases}0, &m\neq n \\\displaystyle \int_{a}^{b} f^2_n(x)\mathrm{d}x>0, &m=n\end{cases} ∫abfm(x)fn(x)dx=⎩ ⎨ ⎧0,∫abfn2(x)dx>0,m=nm=n
则称 { f n ( x ) } \{f_n(x)\} {fn(x)}是 [ a , b ] [a,b] [a,b]上的正交函数列。当 { f n ( x ) } \{f_n(x)\} {fn(x)}是 n n n次多项式时,则称 { f n ( x ) } \{f_n(x)\} {fn(x)}是 [ a , b ] [a,b] [a,b]上的正交多项式列。
n阶Legendre多项式在 [ − 1 , 1 ] [-1,1] [−1,1]上的正交性证明
n次Legendre多项式的定义如下:
p n ( x ) = 1 2 n n ! d n d x n ( x 2 − 1 ) n , n ∈ N p_{n}(x)=\frac{1}{2^n n!}\frac{\mathrm d^n}{\mathrm{d} x^n}(x^2-1)^n, n\in \mathbb{N} pn(x)=2nn!1dxndn(x2−1)n,n∈N
不妨设 n ≥ m n \geq m n≥m。首先构造如下函数
I m n = m ! n ! 2 m 2 n ∫ − 1 1 p m ( x ) p n ( x ) d x = ∫ − 1 1 d m d x m ( x 2 − 1 ) m ⋅ d n d x n ( x 2 − 1 ) n d x \begin{equation} I_{mn}=m!n!2^m2^n\int_{-1}^{1}p_{m}(x)p_{n}(x) \mathrm{d}x =\int_{-1}^{1}\frac{\mathrm d^m}{\mathrm{d} x^m}(x^2-1)^m \cdot \frac{\mathrm d^n}{\mathrm{d} x^n}(x^2-1)^n \mathrm{d}x \end{equation} Imn=m!n!2m2n∫−11pm(x)pn(x)dx=∫−11dxmdm(x2−1)m⋅dxndn(x2−1)ndx
用分部积分法对 ( 1 ) (1) (1)式进行积分,可以得到
I m n = ∫ − 1 1 d m d x m ( x 2 − 1 ) m d ( d n − 1 d x n − 1 ( x 2 − 1 ) n ) = d m d x m ( x 2 − 1 ) m ⋅ d n − 1 d x n − 1 ( x 2 − 1 ) n ∣ − 1 1 − ∫ − 1 1 d n − 1 d x n − 1 ( x 2 − 1 ) n ⋅ d m + 1 d x m + 1 ( x 2 − 1 ) m d x \begin{equation} \begin{align} I_{mn} &=\int_{-1}^{1}\frac{\mathrm d^m}{\mathrm{d} x^m}(x^2-1)^m \mathrm{d}(\frac{\mathrm d^{n-1}}{\mathrm{d} x^{n-1}}(x^2-1)^n) \nonumber \\ &=\left.\frac{\mathrm d^m}{\mathrm{d} x^m}(x^2-1)^m \cdot \frac{\mathrm d^{n-1}}{\mathrm{d} x^{n-1}}(x^2-1)^n \right |_{-1}^{1} \nonumber -\int_{-1}^{1}\frac{\mathrm d^{n-1}}{\mathrm{d} x^{n-1}}(x^2-1)^n \cdot \frac{\mathrm d^{m+1}}{\mathrm{d} x^{m+1}}(x^2-1)^m\mathrm{d}x \nonumber \\ \end{align} \end{equation} Imn=∫−11dxmdm(x2−1)md(dxn−1dn−1(x2−1)n)=dxmdm(x2−1)m⋅dxn−1dn−1(x2−1)n −11−∫−11dxn−1dn−1(x2−1)n⋅dxm+1dm+1(x2−1)mdx
这里引用《n次Legendre(勒让德)多项式在区间(-1, 1)上根的分布及证明》这篇文章里的结论:
当 k < n k<n k<n时, f k ( x ) = [ ( x 2 − 1 ) n ] ( k ) f_{k}(x)=[(x^2-1)^n]^{(k)} fk(x)=[(x2−1)n](k)的每一项都包含因式 x − 1 x-1 x−1与 x + 1 x+1 x+1
因此 d m d x m ( x 2 − 1 ) m ⋅ d n − 1 d x n − 1 ( x 2 − 1 ) n ∣ − 1 1 = 0 \displaystyle \left.\frac{\mathrm d^m}{\mathrm{d} x^m}(x^2-1)^m \cdot \frac{\mathrm d^{n-1}}{\mathrm{d} x^{n-1}}(x^2-1)^n \right |_{-1}^{1}=0 dxmdm(x2−1)m⋅dxn−1dn−1(x2−1)n −11=0。于是 ( 2 ) (2) (2)式可以写成:
I m n = − ∫ − 1 1 d n − 1 d x n − 1 ( x 2 − 1 ) n ⋅ d m + 1 d x m + 1 ( x 2 − 1 ) m d x \begin{equation} I_{mn}=-\int_{-1}^{1}\frac{\mathrm d^{n-1}}{\mathrm{d} x^{n-1}}(x^2-1)^n \cdot \frac{\mathrm d^{m+1}}{\mathrm{d} x^{m+1}}(x^2-1)^m\mathrm{d}x \end{equation} Imn=−∫−11dxn−1dn−1(x2−1)n⋅dxm+1dm+1(x2−1)mdx
继续用分部积分法对 ( 3 ) (3) (3)式重复上述过程,执行 n n n次后,得到
I m n = ( − 1 ) n ∫ − 1 1 d m + n d x m + n ( x 2 − 1 ) m ⋅ ( x 2 − 1 ) n d x \begin{equation} I_{mn}=(-1)^n\int_{-1}^{1} \frac{\mathrm d^{m+n}}{\mathrm{d} x^{m+n}}(x^2-1)^m \cdot (x^2-1)^n \mathrm{d}x \end{equation} Imn=(−1)n∫−11dxm+ndm+n(x2−1)m⋅(x2−1)ndx
下面分情况讨论。
- 若 n > m n>m n>m, d m + n d x m + n ( x 2 − 1 ) m = 0 \displaystyle \frac{\mathrm d^{m+n}}{\mathrm{d} x^{m+n}}(x^2-1)^m =0 dxm+ndm+n(x2−1)m=0,即 I m n = 0 I_{mn}=0 Imn=0,因此有
∫ − 1 1 p m ( x ) p n ( x ) d x = 0 \begin{equation} \int_{-1}^{1}p_{m}(x)p_{n}(x) \mathrm{d}x =0 \end{equation} ∫−11pm(x)pn(x)dx=0
- 若 n = m n=m n=m,根据高阶导数的Leibniz公式可以得到:
d m + n d x m + n ( x 2 − 1 ) m = ∑ i = 0 2 n C 2 n i [ ( x + 1 ) n ] ( i ) [ ( x − 1 ) n ] ( 2 n − i ) = C 2 n n [ ( x + 1 ) n ] ( n ) [ ( x − 1 ) n ] ( n ) = ( 2 n ) ! \begin{equation} \displaystyle \frac{\mathrm d^{m+n}}{\mathrm{d} x^{m+n}}(x^2-1)^m =\displaystyle \sum_{i=0}^{2n} C_{2n}^{i}[(x+1)^n]^{(i)}[(x-1)^n]^{(2n-i)}=C_{2n}^{n}[(x+1)^n]^{(n)}[(x-1)^n]^{(n)}=(2n)! \end{equation} dxm+ndm+n(x2−1)m=i=0∑2nC2ni[(x+1)n](i)[(x−1)n](2n−i)=C2nn[(x+1)n](n)[(x−1)n](n)=(2n)!
将 ( 6 ) (6) (6)式代入 ( 4 ) (4) (4)式,不断使用分部积分法后可以得到
I n n = ( 2 n ) ! ( − 1 ) n ∫ − 1 1 ( x − 1 ) n ( x + 1 ) n d x = ( 2 n ) ! ∫ − 1 1 ( 1 − x ) n d ( ( 1 + x ) n + 1 n + 1 ) = ( 2 n ) ! n + 1 ( 1 − x ) n ( 1 + x ) n + 1 ∣ − 1 1 + ( 2 n ) ! n n + 1 ∫ − 1 1 ( 1 − x ) n − 1 ( 1 + x ) n + 1 d x = ( 2 n ) ! n n + 1 ∫ − 1 1 ( 1 − x ) n − 1 ( 1 + x ) n + 1 d x = ( 2 n ) ! n ( n − 1 ) ( n + 1 ) ( n + 2 ) ∫ − 1 1 ( 1 − x ) n − 2 ( 1 + x ) n + 2 d x = . . . = ( n ! ) 2 ∫ − 1 1 ( 1 + x ) 2 n d x = ( n ! ) 2 2 2 n + 1 2 n + 1 \begin{equation} \begin{align} I_{nn} &= (2n)!(-1)^n\int_{-1}^{1} (x-1)^n (x+1)^n \mathrm{d}x \nonumber \\ &=(2n)!\int_{-1}^{1}(1-x)^n \mathrm{d}\left(\dfrac{(1+x)^{n+1}} {n+1}\right)\nonumber \\ &=\left.\dfrac{(2n)!}{n+1}(1-x)^n(1+x)^{n+1}\right|_{-1}^{1}+\dfrac{(2n)!n}{n+1}\int_{-1}^{1}(1-x)^{n-1}(1+x)^{n+1}\mathrm{d}x \nonumber \\ &=\dfrac{(2n)!n}{n+1}\int_{-1}^{1}(1-x)^{n-1}(1+x)^{n+1}\mathrm{d}x \nonumber \\ &=\dfrac{(2n)!n(n-1)}{(n+1)(n+2)}\int_{-1}^{1}(1-x)^{n-2}(1+x)^{n+2}\mathrm{d}x \nonumber \\ &=... \nonumber \\ &=(n!)^2\int_{-1}^{1}(1+x)^{2n}\mathrm{d}x =\dfrac{(n!)^2 2^{2n+1}}{2n+1}\nonumber \\ \end{align} \end{equation} Inn=(2n)!(−1)n∫−11(x−1)n(x+1)ndx=(2n)!∫−11(1−x)nd(n+1(1+x)n+1)=n+1(2n)!(1−x)n(1+x)n+1 −11+n+1(2n)!n∫−11(1−x)n−1(1+x)n+1dx=n+1(2n)!n∫−11(1−x)n−1(1+x)n+1dx=(n+1)(n+2)(2n)!n(n−1)∫−11(1−x)n−2(1+x)n+2dx=...=(n!)2∫−11(1+x)2ndx=2n+1(n!)222n+1
将 ( 7 ) (7) (7)式代入 ( 1 ) (1) (1)式,可得
∫ − 1 1 p m ( x ) p n ( x ) d x = I n n ( n ! ) 2 2 n = 2 2 n + 1 > 0 \begin{equation} \int_{-1}^{1}p_{m}(x)p_{n}(x) \mathrm{d}x =\dfrac{I_{nn}}{(n!)2^{2n}}=\dfrac{2}{2n+1}>0 \end{equation} ∫−11pm(x)pn(x)dx=(n!)22nInn=2n+12>0
结合 ( 5 ) , ( 8 ) (5),(8) (5),(8)式,我们得到了如下结论
∫ − 1 1 p m ( x ) p n ( x ) d x = { 0 , m ≠ n 2 2 n + 1 > 0 , m = n \int_{-1}^{1}p_{m}(x)p_{n}(x) \mathrm{d}x=\begin{cases}0, &m\neq n \\\displaystyle\dfrac{2}{2n+1}>0, &m=n\end{cases} ∫−11pm(x)pn(x)dx=⎩ ⎨ ⎧0,2n+12>0,m=nm=n
根据定义,我们得到 n n n次Legendre多项式列 { p n ( x ) } \{p_n(x)\} {pn(x)}是 [ − 1 , 1 ] [-1,1] [−1,1]上的正交多项式列。证毕。
相关文章:

n阶Legendre多项式正交性的证明
前言 在《n次Legendre(勒让德)多项式在区间(-1, 1)上根的分布及证明》这篇文章中,我们阐述了Legendre多项式在 [ − 1 , 1 ] [-1,1] [−1,1]上的根分布情况并给出了证明。本文将证明Legendre多项式在 [ − 1 , 1 ] [-1,1] [−1,1]上的正交性质。 正交多项式的定义…...
HarmonyOS NEXT - Dialog 和完全自定义弹框
demo 地址: https://github.com/iotjin/JhHarmonyDemo 组件对应代码实现地址 代码不定时更新,请前往github查看最新代码 在demo中这些组件和工具类都通过module实现了,具体可以参考HarmonyOS NEXT - 通过 module 模块化引用公共组件和utils HarmonyOS NE…...

内容与资讯API优质清单
作为开发者,拥有一套API合集是必不可少的。这个开发者必备的API合集汇集了各种实用的API资源,为你的开发工作提供了强大的支持!无论你是在构建网站、开发应用还是进行数据分析,这个合集都能满足你的需求。你可以通过这些免费API获…...
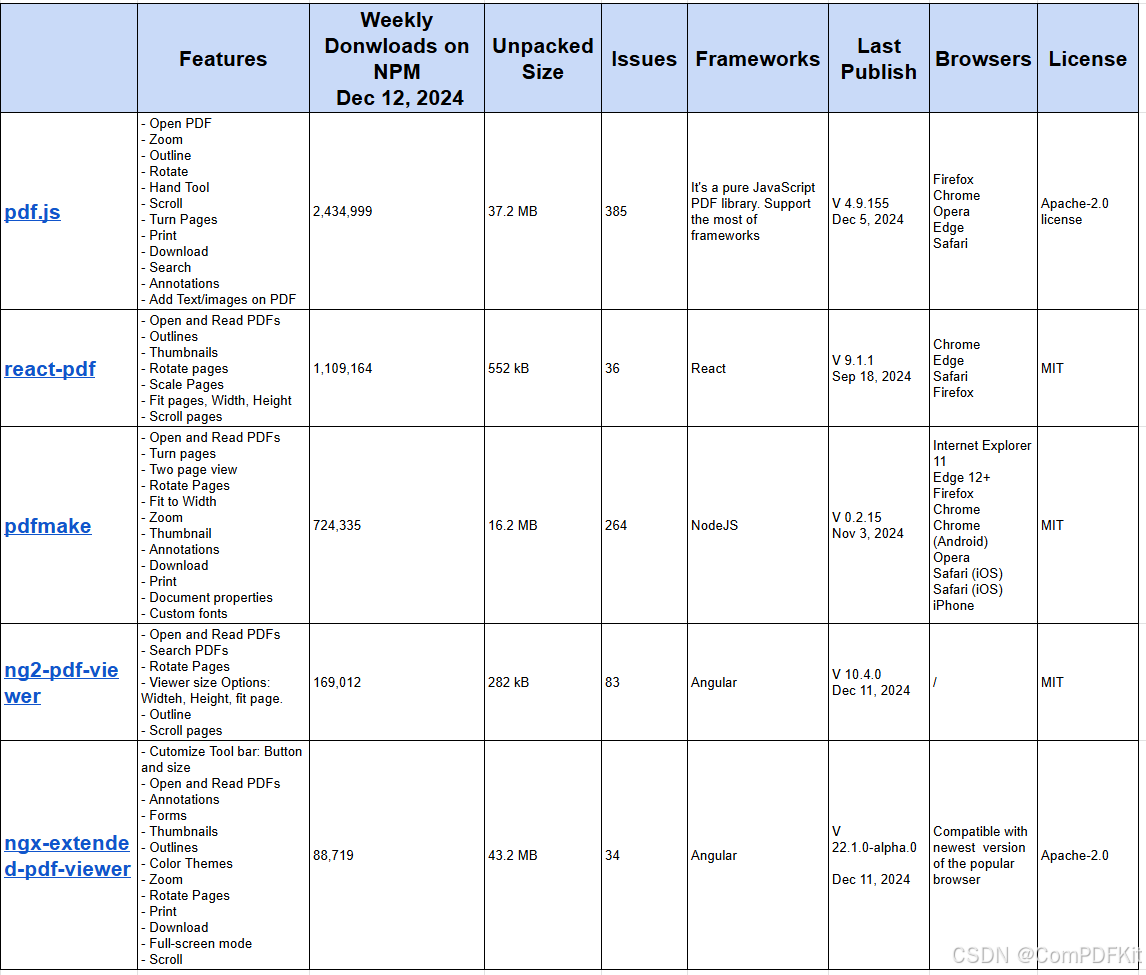
开源 JS PDF 库比较
原文查看:开源JavaScript PDF Library对比 对于需要高性能、复杂功能或强大支持处理复杂 PDF 的项目,建议选择商业 PDF 库, 如ComPDFKit for Web。但是,如果您的目标只是在 Web 应用程序中显示 PDF,则可以使用几个可靠的开源…...
AnaPico信号源在通信测试中的应用案例
AnaPico信号源在通信测试中的应用案例广泛,涉及多种通信技术和测试需求。以下是一些具体的应用实例: 1. APPH系列信号源分析仪(相位噪声分析仪) APPH系列是一款高性能相位噪声分析仪和VCO测试仪,其不同型号的频率范围…...

《智启新材:人工智能重塑分子结构设计蓝图》
在当今科技飞速发展的时代,新材料的研发宛如一场激烈的竞赛,而人工智能(AI)作为一匹黑马,正以前所未有的速度和力量驰骋于这片赛场,为新材料的分子结构设计带来了革命性的突破,成为推动行业发展…...
进阶岛-L2G5000
茴香豆:企业级知识库问答工具 茴香豆本地标准版搭建 环境搭建 安装茴香豆 知识库创建 测试知识助手 Gradio UI 界面测试...

单点登录平台Casdoor搭建与使用,集成gitlab同步创建删除账号
一,简介 一般来说,公司有很多系统使用,为了实现统一的用户名管理和登录所有系统(如 GitLab、Harbor 等),并在员工离职时只需删除一个主账号即可实现权限清除,可以采用 单点登录 (SSO) 和 集中式…...
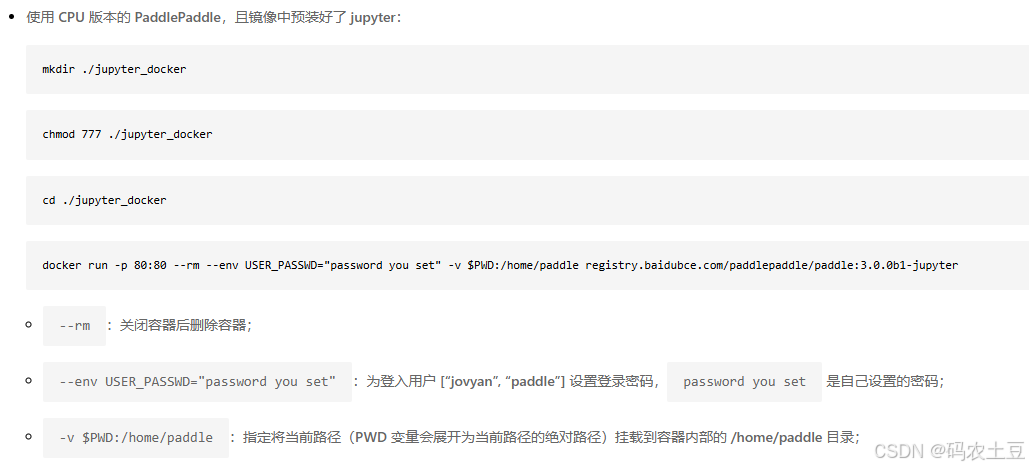
PaddlePaddle飞桨Linux系统Docker版安装
PaddlePaddle飞桨Linux系统Docker版安装 最近学习和了解PP飞桨,一切从安装开始。官网的安装教程很详细: https://www.paddlepaddle.org.cn/install/quick?docurl/documentation/docs/zh/install/docker/linux-docker.html 记录我在安装过程中遇到的问题…...

一款基于.NET开发的简易高效的文件转换器
前言 今天大姚给大家分享一款基于.NET开发的免费(GPL-3.0 license)、简易、高效的文件转换器,允许用户通过Windows资源管理器的上下文菜单来转换和压缩一个或多个文件:FileConverter。 使用技术栈 ffmpeg:作为文件转换…...

Spring Boot教程之三十一:入门 Web
Spring Boot – 入门 Web 如今,大多数应用程序都需要模型-视图-控制器(MVC) 架构来满足各种需求,例如处理用户数据、提高应用程序效率、为应用程序提供动态特性。它主要用于构建桌面图形用户界面 (GUI),但现在越来越流行用于构建基于 Web 的…...

青少年编程与数学 02-004 Go语言Web编程 20课题、单元测试
青少年编程与数学 02-004 Go语言Web编程 20课题、单元测试 一、单元测试(Unit Testing)二、集成测试(Integration Testing)三、区别四、Go Web单元测试使用testing包使用testify框架使用GoConvey框架 五、应用示例步骤 1: 创建HTT…...

概率论 期末 笔记
第一章 随机事件及其概率 利用“四大公式”求事件概率 全概率公式与贝叶斯公式 伯努利概型求概率 习题 推导 一维随机变量及其分布 离散型随机变量(R.V)求分布律 利用常见离散型分布求概率 连续型R.V相关计算 利用常见连续型分布的计算 均匀分布 正态…...

Typesense:开源的高速搜索引擎
在当今数据驱动的世界中,高效、快速且智能的搜索能力是任何应用程序和网站成功的关键因素之一。无论是电商平台、内容管理系统还是社交媒体,用户都希望能够迅速找到所需信息。Typesense,作为一款优秀的开源搜索引擎,旨在通过其卓越…...

【vue】圆环呼吸灯闪烁效果(模拟扭蛋机出口处灯光)
效果图先发: 页面部分: <div ref"round" class"round"><div class"light" ref"light"/><div class"box"></div></div>js部分(控制圆环生成); setRound…...
飞牛 fnos 使用docker部署 Watchtower 自动更新 Docker 容器
Watchtower 简介 Watchtower 是一款开源的 Docker 容器管理工具,主要功能为自动更新运行中的 Docker 容器,支持自动拉取镜像并更新容器、配置邮件通知以及定时执行容器更新任务。 用 compose 搭建 Watchtower 的步骤 新建文件夹:在任意位置…...
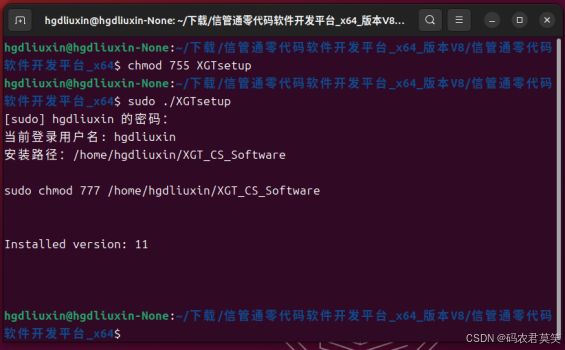
《信管通低代码信息管理系统开发平台》Linux环境安装说明
1 简介 信管通低代码信息管理系统应用平台提供多环境软件产品开发服务,包括单机、局域网和互联网。我们专注于适用国产硬件和操作系统应用软件开发应用。为事业单位和企业提供行业软件定制开发,满足其独特需求。无论是简单的应用还是复杂的系统ÿ…...
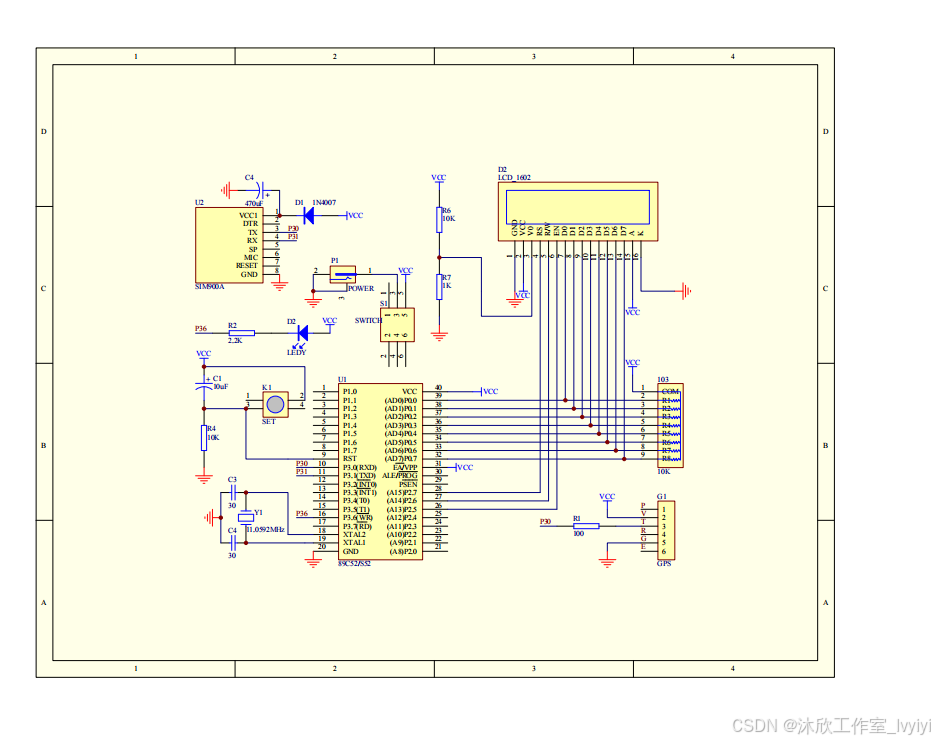
基于物联网的车辆定位和防盗报警系统(论文+源码)
1 系统概述 本文的主要内容是设计一个基于物联网的车辆定位和防盗报警系统,主要是利用STC89C52单片机来作为整体的核心控制元件,主要的核心控制模块主要由GSM通信模块,GPS定位模块,热释电红外检测模块,报警模块以及其他…...
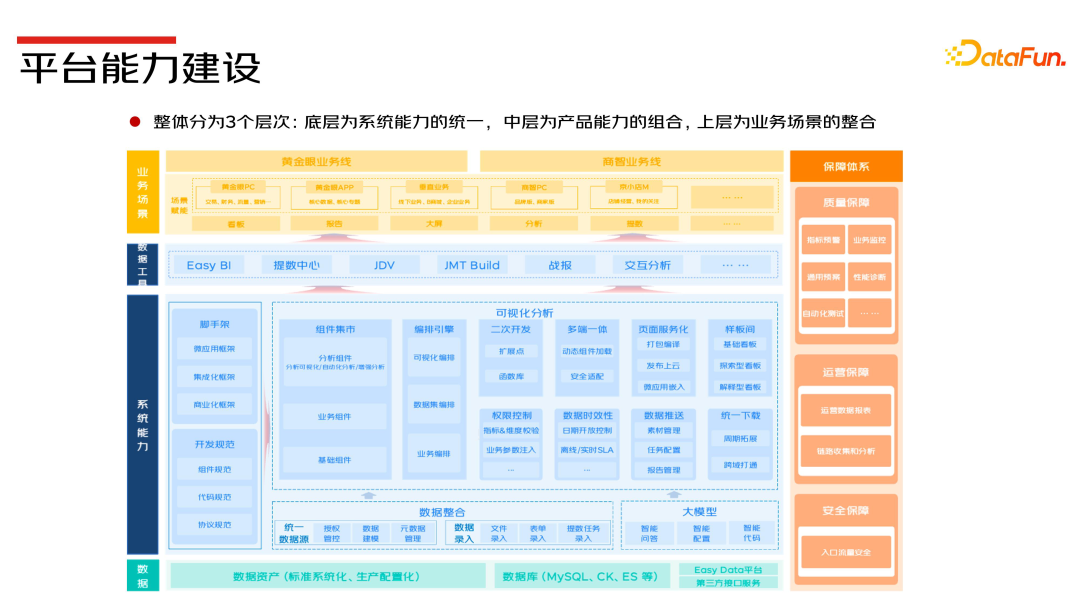
京东零售数据可视化平台产品实践与思考
导读 本次分享题目为京东零售数据可视化平台产品实践与思考。 主要包括以下四个部分: 1. 平台产品能力介绍 2. 业务赋能案例分享 3. 平台建设挑战与展望 作者:梁臣 京东 数据产品架构师 01平台产品能力介绍 1. 产品矩阵 数据可视化产品是一种利用…...
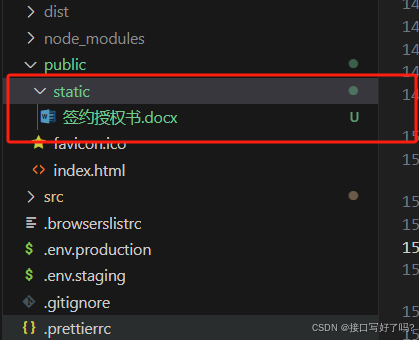
Vue中使用a标签下载静态资源文件(比如excel、pdf等),纯前端操作
第一步,public文件夹下新建static文件夹存放静态资源 我存放了一个 .docx文件,当然,你可以存放pdf/word 等文件都可以。 第二步,模拟a标签下载 //html部分<el-button type"primary" plain click"download&quo…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
