3DMAX镂空星花球建模插件FloralStarBall使用方法
3DMAX镂空星花球建模插件FloralStarBall使用教程

就是那个3DMAX镂空星花球建模,再也不用手动做了,使用3DMAX镂空星花球建模FloralStarBall插件可以一键生成!
3DMAX镂空星花球建模插件FloralStarBall,经典星形球体的美丽变体。星形图案以花卉风格排列,赋予物体独特的视觉美感。它将成为任何Math Art收藏、桌面展品甚至柔性塑料印刷的应力释放器的绝佳补充。 一键生成竟然不费吹灰之力!
【适用版本】
建议版本3dMax2015及更高版本(不仅限于此范围)
【安装方法】
FloralStarBall插件无需安装,使用时直接拖动插件脚本文件到3dmax视口中打开即可。
【使用方法】
FloralStarBall插件使用方法非常简单,基本是一键生成!
1.打开FloralStarBall插件,设置参数。

①选择生成星花球的类型(样式)。
②设置球体参数。
半径:星花球的半径。
宽度:球体框架的宽度。
厚度:球体框架的厚度。
扭曲1、扭曲2、扭曲3:设置球体框架的弯曲程度。这3个参数大多数情况下不建议调节。调节时需多尝试3者组合,设置不当可能出现生成球体变形或“破面”。
2.点击“创建”按钮,生成!

下面是3种类型图示:

综上所述,3DMAX镂空星花球建模插件FloralStarBall,以其经典星形球体的优雅变体,结合花卉风格的独特排列,不仅为视觉艺术领域带来了耳目一新的美感体验,更是Math Art收藏、桌面装饰乃至柔性塑料印刷应力释放器的理想之选。其一键生成的便捷性,让创作过程变得轻松愉悦,真正实现了艺术与技术的完美融合。
感谢大家阅读,本次3dmax插件教程就分享到这里,下期再会!
相关文章:

3DMAX镂空星花球建模插件FloralStarBall使用方法
3DMAX镂空星花球建模插件FloralStarBall使用教程 就是那个3DMAX镂空星花球建模,再也不用手动做了,使用3DMAX镂空星花球建模FloralStarBall插件可以一键生成! 3DMAX镂空星花球建模插件FloralStarBall,经典星形球体的美丽变体。星形…...

window 安装 nodejs
方式一:使用 fnm 可能会出现 cmd 找不到 nodejs 和 npm 的情况,并且包也可能不知道哪一个 参考链接 Node.js — Download Node.js 使用 powershell 操作,要不然可能有些执行不了 # 安裝 fnm (快速 Node 管理器) winget install Schniz.fnm# …...

Autoware Universe 安装记录
前提: ubuntu20.04,英伟达显卡。 ROS2-Galactic安装 wget http://fishros.com/install -O fishros && . fishros 选择galactic(ROS2)版本,桌面版 ROS2-dev-tools安装 sudo apt install python3-testresources sudo apt update …...

每天40分玩转Django:Django部署概述
一、Django部署概述 在开发阶段,我们通常使用Django内置的轻量级开发服务器runserver。但在生产环境中,为了应对大量并发请求,需要使用高性能的WSGI服务器,如Gunicorn、uWSGI等。同时还要配置Nginx等Web服务器作为反向代理,实现负载均衡、静态文件处理等。下面是Django部署的整…...

使用VS Code开发ThinkPHP项目
【图书介绍】《ThinkPHP 8高效构建Web应用》-CSDN博客 《ThinkPHP 8高效构建Web应用 夏磊 编程与应用开发丛书 清华大学出版社》【摘要 书评 试读】- 京东图书 ThinkPHP 8开发环境安装-CSDN博客 安装ThinkPHP项目的IDE 常用的集成开发环境(IDE)包括P…...

基于深度可分离卷积的MNIST手势识别
基于深度可分离膨胀卷积的MNIST手写体识别 Github链接 项目背景: MNIST手写体数据集是深度学习领域中一个经典的入门数据集,包含了从0到9的手写数字图像,用于评估不同模型在图像分类任务上的性能。在本项目中,我们通过设计一种基…...

Linux服务器pm2 运行chatgpt-on-wechat,搭建微信群ai机器人
安装 1.拉取项目 项目地址: chatgpt-on-wechat 2.安装依赖 pip3 install -r requirements.txt pip3 install -r requirements-optional.txt3、获取API信息 当前免费的有百度的文心一言,讯飞的个人认证提供500万token的额度。 控制台-讯飞开放平台 添加链接描述…...

Word批量更改题注
文章目录 批量更改批量去除空格 在写文章的时候,往往对图片题注有着统一的编码要求,例如以【图 1- xx】。一般会点击【引用】->【插入题注】来插入题注,并且在引用的时候,点击【引用】->【交叉引用】,并且在交叉…...

Springboot配置嵌入式服务器
一.如何定制和修改Servlet容器的相关配置 修改和server有关的配置(ServerProperties); server.port8081 server.context‐path/tx server.tomcat.uri‐encodingUTF‐8 在yml配置文件的写法: server:port: 8081servlet:context-pa…...
正交三角函数全面阐述
目录 1. 正交性定义 2. 正交三角函数 常见的正交三角函数 3. 正交三角函数的特性 4. 正交三角函数在傅里叶分析中的应用 5. 正交三角函数的应用领域 6. 总结 正交三角函数是指在特定条件下,三角函数之间的内积为零。更具体地说,在数学分析、信号处…...

《Vue3 四》Vue 的组件化
组件化:将一个页面拆分成一个个小的功能模块,每个功能模块完成自己部分的独立的功能。任何应用都可以被抽象成一棵组件树。 Vue 中的根组件: Vue.createApp() 中传入对象的本质上就是一个组件,称之为根组件(APP 组件…...
)
linux中,mysql数据库分片(分库分表)
1.mysql分库分表:解决单个mysql存储上限问题1.实现方法:存储层面:利用分布式存储解决方案分库分表:拆分库和表到其它服务器2.常用设计思路:垂直分库(库里面的表分开)水平分表(表里面的数据分开)分库:数据库分为多个,每个数据库里面都有表,数据均匀存储分库分表:在分的每库里面,…...

springboot503基于Sringboot+Vue个人驾校预约管理系统(论文+源码)_kaic
摘 要 传统办法管理信息首先需要花费的时间比较多,其次数据出错率比较高,而且对错误的数据进行更改也比较困难,最后,检索数据费事费力。因此,在计算机上安装个人驾校预约管理系统软件来发挥其高效地信息处理的作用&am…...
Docker应用-项目部署及DockerCompose
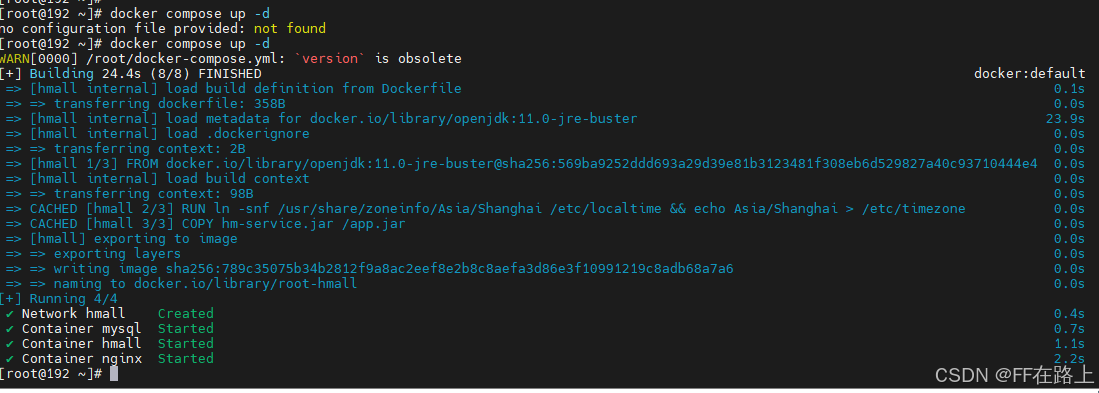
文章目录 Docker应用-项目部署1. 项目部署-后端1.1 修改配置1.2 项目打包1.3 编写Dockerfile1.4 创建镜像1.5 创建并运行容器1.6 测试 2. 项目部署-前端2.1 html前端静态目录2.2 nginx.config编写2.3 部署宿主机服务器2.4 创建容器并挂载2.5 测试 3. DockerCompose3.1 基本语法…...

从0入门自主空中机器人-2-1【无人机硬件框架】
关于本课程: 本次课程是一套面向对自主空中机器人感兴趣的学生、爱好者、相关从业人员的免费课程,包含了从硬件组装、机载电脑环境设置、代码部署、实机实验等全套详细流程,带你从0开始,组装属于自己的自主无人机,并让…...

Kafka高性能设计
高性能设计概述 Kafka高性能是多方面协同的结果,包括集群架构、分布式存储、ISR数据同步及高效利用磁盘和操作系统特性等。主要体现在消息分区、顺序读写、页缓存、零拷贝、消息压缩和分批发送六个方面。 消息分区 存储不受单台服务器限制,能处理更多数据…...

Redis字符串底层结构对数值型的支持常用数据结构和使用场景
字符串底层结构 SDS (Simple Dynamic Strings) 是 Redis 中用于实现字符串类型的一种数据结构。SDS 的设计目标是提供高效、灵活的字符串操作,同时避免传统 C 字符串的一些缺点。 struct sdshdr {int len; // 已使用的长度int free; // 未使用的长度char bu…...

uniapp 微信小程序 数据空白展示组件
效果图 html <template><view class"nodata"><view class""><image class"nodataimg":src"$publicfun.locaAndHttp()?localUrl:$publicfun.httpUrlImg(httUrl)"mode"aspectFit"></image>&l…...

在vscode的ESP-IDF中使用自定义组件
以hello-world为例,演示步骤和注意事项 1、新建ESP-IDF项目 选择模板 从hello-world模板创建 2、打开项目 3、编译结果没错 正在执行任务: /home/azhu/.espressif/python_env/idf5.1_py3.10_env/bin/python /home/azhu/esp/v5.1/esp-idf/tools/idf_size.py /home…...

目标检测,语义分割标注工具--labelimg labelme
1 labelimg labelimg可以用来标注目标检测的数据集, 提供多种格式的输出, 如Pascal Voc, YOLO等。 1.1 安装 pip install labelimg1.2 使用 命令行直接输入labelimg即可打开软件主界面进行操作。 使用非常简单, 不做过细的介绍࿰…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...
