【机器学习】分类
文章目录
- 1. 能否用回归解决分类问题
- 2. 生成模型(概率生成)
- 3. 判别模型(逻辑回归)
- 4. 多分类问题
1. 能否用回归解决分类问题
二元分类
- 数据分布不规律,回归函数会尽量减少误差,导致不合理的偏移
- 离分界较远的点会影响划分
- 决策边界偏移:难以找到回归函数,使大部分样本点集中在离散点附近
多元分类
- 使用数值描述类别时,存在问题:相近的数值之间可能有联系,但实际分类之间没有隐含关系
2. 生成模型(概率生成)
确定模型
- 贝叶斯公式:根据先验概率求后验概率
P ( C 1 ∣ x ) = P ( C 1 ) P ( x ∣ C 1 ) P ( C 1 ) P ( x ∣ C 1 ) + P ( C 2 ) P ( x ∣ C 2 ) P(C_1|x) = \frac{P(C_1)P(x|C_1)}{P(C_1)P(x|C_1) + P(C_2)P(x|C_2)} P(C1∣x)=P(C1)P(x∣C1)+P(C2)P(x∣C2)P(C1)P(x∣C1)
-
对于二分类问题,只需判断是否属于分类 1,分类 2 即确定
-
目标是找到拟合分布 P ( x ∣ C 1 ) P(x|C_1) P(x∣C1)和 P ( x ∣ C 2 ) P(x|C_2) P(x∣C2)
评估函数
- 高斯分布:寻找 μ \mu μ 和 Σ \Sigma Σ,使得高斯分布与 x 在 C 中的分布最大匹配
- 分别寻找两个分布 C 1 C1 C1, C 2 C2 C2
找到最优的函数
- 极大似然估计法
- 通过代入所有的 x x x 到高斯分布,计算概率的连乘结果,最大化此结果,确定最优的 μ \mu μ 和 Σ \Sigma Σ。
如何实现分类
- 找到高斯分布后,代入问题模型中,确定后验概率函数,输入 x x x 就能得到分类结果。
优化
- 共用协方差 Σ \Sigma Σ:减少参数,防止过拟合。
- 这时找到的函数将会是一条直线。
3. 判别模型(逻辑回归)
说明
- 当共用协方差时,可以得到如下公式:
P ( C 1 ∣ x ) = σ ( w x + b ) P(C_1|x) = \sigma(wx + b) P(C1∣x)=σ(wx+b)
-
其中, σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1 + e^{-x}} σ(x)=1+e−x1 为 Sigmoid 函数。
-
直接训练 w w w 和 b b b,无需假设高斯分布。
做法
-
确定模型:
f ( x ) = P ( C 1 ∣ x ) = σ ( w x + b ) f(x) = P(C_1|x) = \sigma(wx + b) f(x)=P(C1∣x)=σ(wx+b)
目标是直接找 w w w 和 b b b 来确定后验概率。
-
评估函数:
L ( w , b ) = f w , b ( x 1 ) f w , b ( x 2 ) ( 1 − f w , b ( x 3 ) ) . . . L(w,b)=f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3))... L(w,b)=fw,b(x1)fw,b(x2)(1−fw,b(x3))...
此时目标是最大化评估函数。引入交叉熵(Cross-Entropy):
H ( p , q ) = − ∑ p ( x ) ln ( q ( x ) ) H(p,q) = - \sum p(x) \ln(q(x)) H(p,q)=−∑p(x)ln(q(x))- 交叉熵越小,表示两个分布越接近。
进一步损失函数:
− ln L ( w , b ) = − ∑ [ y n ln f w , b ( x n ) + ( 1 − y n ) ln ( 1 − f w , b ( x n ) ) ] -\ln L(w,b) = - \sum \left[ y^n \ln f_{w,b}(x^n) + (1 - y^n) \ln(1 - f_{w,b}(x^n)) \right] −lnL(w,b)=−∑[ynlnfw,b(xn)+(1−yn)ln(1−fw,b(xn))]
- 目标是最小化损失函数。
-
寻找最优函数
- 使用梯度下降法更新参数:
w t + 1 = w t − η ∑ n [ − ( y n − f w , b ( x n ) ) x n ] w_{t+1} = w_t - \eta \sum_n \left[ -(y^n - f_{w,b}(x^n)) x^n \right] wt+1=wt−ηn∑[−(yn−fw,b(xn))xn]
与线性回归比较
- 逻辑回归中引入了 Sigmoid 函数,输出值范围为 0 到 1。
- 线性回归输出可能是任意实数。
- 逻辑回归的损失函数是交叉熵,而线性回归使用平方误差。
与生成模型比较
- 生成模型假设数据分布符合某个高斯分布。
- 判别模型不做假设,直接学习分类边界(求 w w w 和 b b b)。
- 判别模型通常比生成模型表现好,但在数据不足的情况下,生成模型更为实用。
逻辑回归缺陷
- 逻辑回归无法解决线性不可分问题,需要通过特征转换来处理,这通常是深度学习的核心。
为什么不用平方误差?
-
若用平方误差,损失函数为:
L ( w , b ) = 1 2 ∑ ( y n − f w , b ( x n ) ) 2 L(w,b) = \frac{1}{2} \sum (y^n - f_{w,b}(x^n))^2 L(w,b)=21∑(yn−fw,b(xn))2
梯度为:
d L d w = 2 ( y n − f w , b ( x n ) ) f w , b ( x n ) ( 1 − f w , b ( x n ) ) x n \frac{dL}{dw} = 2(y^n - f_{w,b}(x^n)) f_{w,b}(x^n) (1 - f_{w,b}(x^n)) x^n dwdL=2(yn−fw,b(xn))fw,b(xn)(1−fw,b(xn))xn
-
当 y n = 1 y^n = 1 yn=1 且 f ( x n ) = 1 f(x^n) = 1 f(xn)=1 时,梯度为 0(正常)。
-
当 y n = 1 y^n = 1 yn=1 且 f ( x n ) = 0 f(x^n) = 0 f(xn)=0 时,梯度也为 0(不正常,训练非常缓慢)。
-
结论:使用平方误差损失函数,梯度会在边界附近为零,导致训练速度非常慢。交叉熵的损失函数更适合分类问题。
4. 多分类问题
- 使用 逻辑回归 计算每个类别的概率值,然后通过 Softmax 函数选择最大概率的类别。
- Softmax ( x i ) = e x i ∑ j e x j \text{Softmax}(x_i) = \frac{e^{x_i}}{\sum_j e^{x_j}} Softmax(xi)=∑jexjexi
相关文章:

【机器学习】分类
文章目录 1. 能否用回归解决分类问题2. 生成模型(概率生成)3. 判别模型(逻辑回归)4. 多分类问题 1. 能否用回归解决分类问题 二元分类 数据分布不规律,回归函数会尽量减少误差,导致不合理的偏移离分界较远…...

5.若依的角色权限控制
RBAC 基于角色的访问控制,通过角色来分配和管理用户的菜单权限。 修改课程管理的菜单到主类目下 新建角色并分配菜单 新建用户并分配角色 添加一个根菜单,父级为主类目...

Lumos学习王佩丰Excel第二十三讲:饼图美化与PPT图表
一、双坐标柱形图的补充知识 1、主次坐标设置 2、主次坐标柱形避让(通过增加两个系列,挤压使得两个柱形挨在一起) 增加两个系列 将一个系列设置成主坐标轴,另一个设成次坐标轴 调整系列位置 二、饼图美化 1、饼图美化常见设置 …...

安装winserver2008R2虚拟机步骤
一、服务器系统介绍 1.1什么是服务器? 服务器英文名称为“Server”,指的是网络环境下为客户机(Client)提供某种服务的专用计算机,服务器安装有网络操作系统(如Windows 2000 Server、Linux、Unix等)和各种服务器应用系统软件(如Web服务、电子…...

ACPI PM Timer
ACPI PM Timer 概述: ACPI PM Timer是一个非常简单的计时器,它以 3.579545 MHz 运行,在计数器溢出时生成系统控制中断(SCI)。它精度较低,建议使用其他定时器,如HPET或APIC定时器。 检测ACPI P…...

Linux 和设备树
“开放固件设备树”,简称 Devicetree (DT),是一种用于描述硬件的数据结构和语言。更具体地说,它是操作系统可读取的硬件描述,因此操作系统无需对机器的详细信息进行硬编码。 从结构上看,DT 是一棵树,或具有…...

Qt仿音乐播放器:QFileDialog添加本地文件
一、套路 QFileDialog fileDialog(this);// 创建对话框,并设置父元素;fileDialog.setWindowTitle("添加本地下载的音乐");//设置窗口标题//设置文件对话框的默认打开路径 QString projectPathQDir::currentPath();//获取当前目录 QDir dir(pr…...

Odoo 引用字段 fields.Reference:动态关系的选择器
在 Odoo 模型开发中,关系型字段是构建复杂应用的基础。 然而,传统的 m2o、o2m 和 m2m 字段需要在模型定义时就明确指定关系的目标模型,这在某些场景下会显得不够灵活。 为了解决这个问题,Odoo 提供了 fields.Reference 引用字段&a…...

Android笔试面试题AI答之Android基础(6)
Android入门请看《Android应用开发项目式教程》 文章目录 1.Android Studio版本与Gradle版本有什么关联?**1. Gradle 的作用****2. Android Studio 与 Gradle 的关系****3. 版本对应关系****4. 如何查看和修改版本****查看当前版本****修改版本** **5. 版本不兼容的…...

C# 中的记录类型简介 【代码之美系列】
🎀🎀🎀代码之美系列目录🎀🎀🎀 一、C# 命名规则规范 二、C# 代码约定规范 三、C# 参数类型约束 四、浅析 B/S 应用程序体系结构原则 五、浅析 C# Async 和 Await 六、浅析 ASP.NET Core SignalR 双工通信 …...

利用Java爬虫速卖通按关键字搜索AliExpress商品
在这个信息爆炸的时代,数据的价值日益凸显。对于电商领域的从业者来说,能够快速获取商品信息成为了一项重要的技能。速卖通(AliExpress)作为全球领先的跨境电商平台,拥有海量的商品数据。本文将介绍如何使用Java语言编…...

gitlab runner 实现 微信小程序自动化部署
微信小程序多人开发的情况下,开发人员都只能在本机上发布体验版,且需要到小程序管理后台自行切换到自己发布的版本,会出现体验版本覆盖的问题。给开发测试带来问题。 miniprogram-ci 的发布,使得开发人员可以通过命令行上传小程序…...

Playwright爬虫xpath获取技巧
示例一 <button class"MuiButtonBase-root MuiButton-root MuiLoadingButton-root MuiButton-contained MuiButton-containedPrimary MuiButton-sizeLarge MuiButton-containedSizeLarge MuiButton-colorPrimary MuiButton-fullWidth MuiButton-root MuiLoadingButton…...

总结TCP/IP四层模型
总结TCP/IP四层模型 阅读目录(Content) 一、TCP/IP参考模型概述 1.1、TCP/IP参考模型的层次结构二、TCP/IP四层功能概述 2.1、主机到网络层 2.2、网络互连层 2.3、传输层 2.3、应用层 三、TCP/IP报文格式 3.1、IP报文格式3.2、TCP数据段格式3.3、UDP数据段格式3.4、套…...

netcat和nmap的区别
Netcat 和 Nmap 是两种广泛使用的网络工具,但它们的功能和使用场景有所不同。下面是这两种工具的对比: Netcat(nc) 用途和功能: 网络连接: Netcat 是一个功能强大的网络工具,用于创建 TCP 或 UDP 连接。可以用来进行网…...
)
MinIO服务器文件复制(Windows环境Linux环境)
一、下载 Windows环境:https://dl.min.io/server/minio/release/windows-amd64/minio.exe Linux环境: > curl https://dl.min.io/client/mc/release/linux-amd64/mc \ --create-dirs \ -o $HOME/minio/mc > chmod x $HOME/minio/mc > expo…...

【机器学习】【朴素贝叶斯分类器】从理论到实践:朴素贝叶斯分类器在垃圾短信过滤中的应用
🌟 关于我 🌟 大家好呀!👋 我是一名大三在读学生,目前对人工智能领域充满了浓厚的兴趣,尤其是机器学习、深度学习和自然语言处理这些酷炫的技术!🤖💻 平时我喜欢动手做实…...

无监督学习算法
K-均值聚类(K-means clustering)是一种常用的无监督学习算法,用于将数据集划分成 K 个不同的组或簇。该算法主要通过计算数据点之间的欧几里得距离来确定数据点之间的相似性,并根据相似性将数据点分配到不同的簇中,使得…...

【Compose multiplatform教程17】【组件】BoxWithConstraints组件
查看全部组件 https://blog.csdn.net/b275518834/article/details/144751353 BoxWithConstraints 功能说明:它是 Jetpack Compose 中的关键布局组件,能够精准捕捉自身所在容器的尺寸约束信息,通过获取最大宽度和最大高度这两个关键属性&…...

银河麒麟操作系统安装达梦数据库(超详细)
目录 引言1. 前期准备1.1 安装麒麟系统1.2 下载达梦数据库安装包(DM8)1.3 上传安装包到麒麟系统1.4 挂载安装包(iso)文件1.5 配置安装用户和组1.6 创建安装路径及修改权限1.7 设置临时安装目录 2. 安装达梦数据库(DM8&…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...
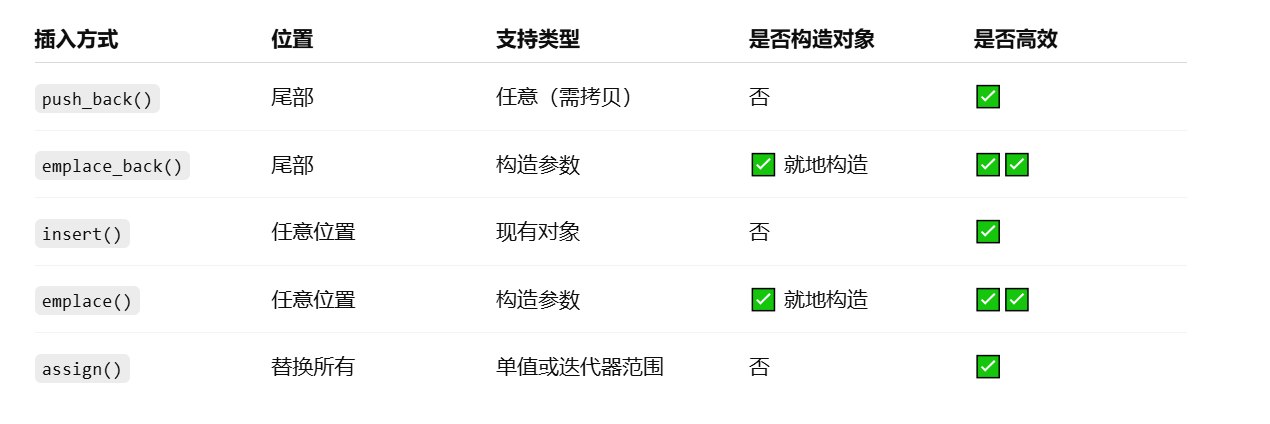
C++中vector类型的介绍和使用
文章目录 一、vector 类型的简介1.1 基本介绍1.2 常见用法示例1.3 常见成员函数简表 二、vector 数据的插入2.1 push_back() —— 在尾部插入一个元素2.2 emplace_back() —— 在尾部“就地”构造对象2.3 insert() —— 在任意位置插入一个或多个元素2.4 emplace() —— 在任意…...
OPENCV图形计算面积、弧长API讲解(1)
一.OPENCV图形面积、弧长计算的API介绍 之前我们已经把图形轮廓的检测、画框等功能讲解了一遍。那今天我们主要结合轮廓检测的API去计算图形的面积,这些面积可以是矩形、圆形等等。图形面积计算和弧长计算常用于车辆识别、桥梁识别等重要功能,常用的API…...

若依项目部署--传统架构--未完待续
若依项目介绍 项目源码获取 #Git工具下载 dnf -y install git #若依项目获取 git clone https://gitee.com/y_project/RuoYi-Vue.git项目背景 随着企业信息化需求的增加,传统开发模式存在效率低,重复劳动多等问题。若依项目通过整合主流技术框架&…...
