无监督学习算法
K-均值聚类(K-means clustering)是一种常用的无监督学习算法,用于将数据集划分成 K 个不同的组或簇。该算法主要通过计算数据点之间的欧几里得距离来确定数据点之间的相似性,并根据相似性将数据点分配到不同的簇中,使得簇内的数据点相似度尽可能高,而簇间的数据点相似度尽可能低。
K-均值聚类算法的步骤如下:
1. 随机选择 K 个中心点作为初始的聚类中心。
2. 对于每个数据点,计算其与每个聚类中心的距离,并将其分配到最近的聚类中心所代表的簇中。
3. 更新每个簇的聚类中心,计算该簇中所有数据点的均值,并将其作为新的聚类中心。
4. 重复步骤2和3,直到达到停止条件(如聚类中心不再改变或达到指定的迭代次数)。
K-均值聚类算法的优点:
1. 简单易实现:K-均值算法的实现相对简单,易于理解和编程。
2. 可扩展性:适用于大规模数据集,并且可以通过调整 K 的值来控制聚类的数量。
3. 对于球状簇效果好:对于数据分布为球状的数据集,K-均值算法可以得到较好的聚类效果。
K-均值聚类算法的缺点:
1. 对于非球状簇效果差:当数据集中存在非球状的簇时,K-均值算法的聚类效果会变差,因为它假设每个簇都是以聚类中心为中心的球形。
2. 对初始聚类中心敏感性:K-均值算法对初始聚类中心的选择非常敏感,不同的初始选择可能导致不同的聚类结果。
3. 需要提前确定 K 的值:K-均值算法需要提前确定聚类的数量 K,但在实际应用中,我们通常无法事先准确地知道应该选择多少个聚类。
总结一下,K-均值聚类算法是一种简单而可扩展的聚类算法,适用于球形簇的数据集,但对非球状簇的数据集效果差。它还对初始聚类中心的选择敏感,并且需要事先确定聚类的数量 K。
相关文章:

无监督学习算法
K-均值聚类(K-means clustering)是一种常用的无监督学习算法,用于将数据集划分成 K 个不同的组或簇。该算法主要通过计算数据点之间的欧几里得距离来确定数据点之间的相似性,并根据相似性将数据点分配到不同的簇中,使得…...

【Compose multiplatform教程17】【组件】BoxWithConstraints组件
查看全部组件 https://blog.csdn.net/b275518834/article/details/144751353 BoxWithConstraints 功能说明:它是 Jetpack Compose 中的关键布局组件,能够精准捕捉自身所在容器的尺寸约束信息,通过获取最大宽度和最大高度这两个关键属性&…...

银河麒麟操作系统安装达梦数据库(超详细)
目录 引言1. 前期准备1.1 安装麒麟系统1.2 下载达梦数据库安装包(DM8)1.3 上传安装包到麒麟系统1.4 挂载安装包(iso)文件1.5 配置安装用户和组1.6 创建安装路径及修改权限1.7 设置临时安装目录 2. 安装达梦数据库(DM8&…...

Spring源码_05_IOC容器启动细节
前面几章,大致讲了Spring的IOC容器的大致过程和原理,以及重要的容器和beanFactory的继承关系,为后续这些细节挖掘提供一点理解基础。掌握总体脉络是必要的,接下来的每一章都是从总体脉络中, 去研究之前没看的一些重要…...

科大讯飞在线语音合成(流式版)python版
1、进入自己的项目 复制APPID、APISecret、APIKey 2、添加好听发音人 复制vcn参数 3、需要替换代码部分: 换自己喜欢的发声人的参数 换上自己的APPID、APISecret、APIKey 4、完整代码: # -*- coding:utf-8 -*- import _thread as thread import base…...

常见搜索算法汇总
常见搜索算法总结 搜索算法是人工智能和计算机科学中用于解决问题、优化路径或发现数据模式的关键技术。本文将对常见的搜索算法进行总结,包括A*算法、D*算法、模拟退火(Simulated Annealing)、爬山法(Hill Climbing)、…...

vue 中 ref 详解
一、定义与基本用法 1. 定义 在 Vue.js 中,ref是一个用于在组件中获取 DOM 元素或者子组件实例引用的属性。它提供了一种直接访问元素或组件的方式,使得我们可以在 JavaScript 代码中对它们进行操作。 2. 基本使用 在模板中,可以通过给元…...

探索开源项目 kernel:技术的基石与无限可能
在开源的广袤世界中,有一颗璀璨的明星——kernel(https://gitee.com/openeuler/kernel),它宛如一座技术的宝藏,蕴含着无数的智慧与创新,为众多开发者所瞩目和敬仰。 一、初窥 kernel 项目 当我第一次接触…...

C 实现植物大战僵尸(二)
C 实现植物大战僵尸(二) 前文链接,C 实现植物大战僵尸(一) 五 制作启动菜单 启动菜单函数 void startUI() {IMAGE imageBg, imgMenu1, imgMenu2;loadimage(&imageBg, "res/menu.png");loadimage(&am…...

Vivado - TCL 命令(DPU脚本、v++命令、impl策略)
目录 1. 简介 2. TCL 示例 2.1 DPU TCL 脚本 2.1.1 源码-精简 2.1.2 依赖关系 2.1.3 查 v 步骤列表 2.1.4 生成 DPU.XO 2.2 CPU 示例 2.2.1 源码-框架 2.2.2 示例设计详解 2.3 创建运行脚本 2.3.1 Generate scripts 2.3.2 runme.sh 文件 2.3.3 design_1_wrapper…...

【JDBC】数据库连接的艺术:深入解析数据库连接池、Apache-DBUtils与BasicDAO
文章目录 前言🌍 一.连接池❄️1. 传统获取Conntion问题分析❄️2. 数据库连接池❄️3.连接池之C3P0技术🍁3.1关键特性🍁3.2配置选项🍁3.3使用示例 ❄️4. 连接池之Druid技术🍁 4.1主要特性🍁 4.2 配置选项…...

hadoop-common的下载位置分享
1.GitHub - steveloughran/winutils: Windows binaries for Hadoop versions (built from the git commit ID used for the ASF relase) 2.GitHub - cdarlint/winutils: winutils.exe hadoop.dll and hdfs.dll binaries for hadoop windows 3.winutils: hadoop winutils 镜像...

【机器学习】SVM支持向量机(一)
介绍 支持向量机(Support Vector Machine, SVM)是一种监督学习模型,广泛应用于分类和回归分析。SVM 的核心思想是通过找到一个最优的超平面来划分不同类别的数据点,并且尽可能地最大化离该超平面最近的数据点(支持向量…...

Spring Boot介绍、入门案例、环境准备、POM文件解读
文章目录 1.Spring Boot(脚手架)2.微服务3.环境准备3.1创建SpringBoot项目3.2导入SpringBoot相关依赖3.3编写一个主程序;启动Spring Boot应用3.4编写相关的Controller、Service3.5运行主程序测试3.6简化部署 4.Hello World探究4.1POM文件4.1.1父项目4.1.2父项目的父…...

基于Spring Boot + Vue3实现的在线商品竞拍管理系统源码+文档
前言 基于Spring Boot Vue3实现的在线商品竞拍管理系统是一种现代化的前后端分离架构的应用程序,它结合了Java后端框架Spring Boot和JavaScript前端框架Vue.js的最新版本(Vue 3)。该系统允许用户在线参与商品竞拍,并提供管理后台…...
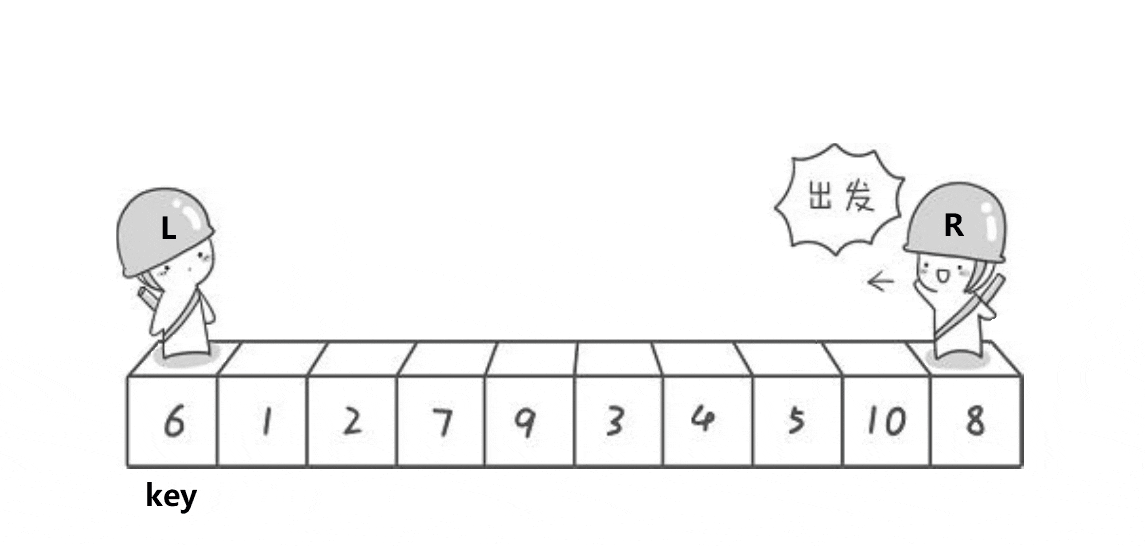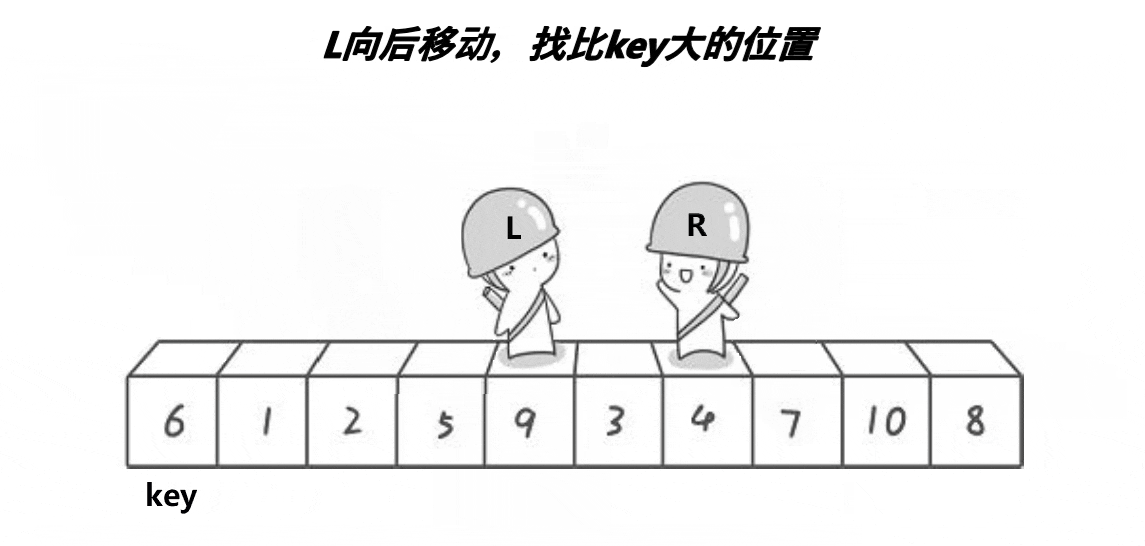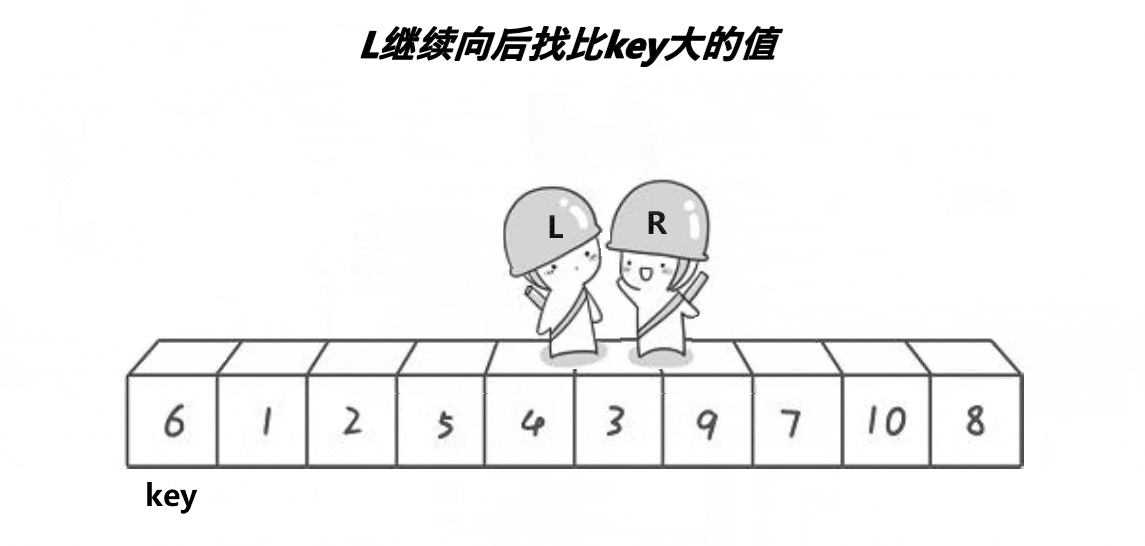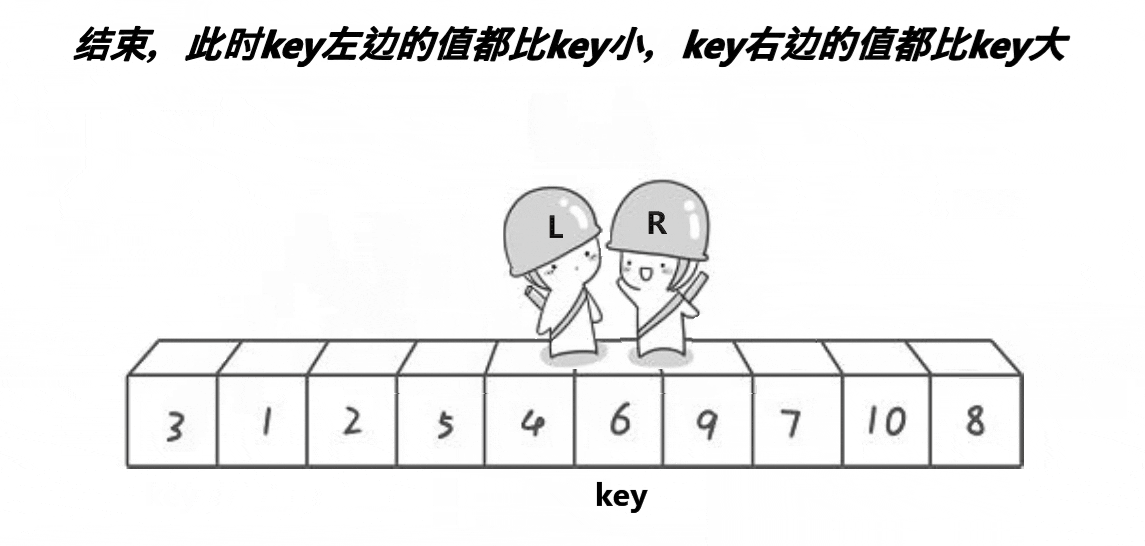
LeetCode--排序算法(堆排序、归并排序、快速排序)
排序算法 归并排序算法思路代码时间复杂度 堆排序什么是堆?如何维护堆?如何建堆?堆排序时间复杂度 快速排序算法思想代码时间复杂度 归并排序 算法思路 归并排序算法有两个基本的操作,一个是分,也就是把原数组划分成…...

华诺星空 Java 开发工程师笔试题 - 解析
单选题 1.Math.round(-11.5)等于多少?(B) A.-11.5 B.-11 C.-12 D.11.5 2.下列哪个没有继承自Collection接口。( C ) A.List B.Set C.Map D.全部 3.下列说法正确的有(B) A.在类方法中可用this来调用本类的类方法 B.在类方法中调用本类的类方法时可直接调用 C.在类…...

QT:一个TCP客户端自动连接的测试模型
版本 1:没有取消按钮 测试效果: 缺陷: 无法手动停止 测试代码 CMakeLists.txt cmake_minimum_required(VERSION 3.19) project(AutoConnect LANGUAGES CXX)find_package(Qt6 6.5 REQUIRED COMPONENTS Core Widgets Network)qt_standard_project_setup(…...

关于启动vue项目,出现:Error [ERR_MODULE_NOT_FOUND]: Cannot find module ‘xxx‘此类错误
目录 一、问题报错 二、原因分析 三、解决方法 一、问题报错 node环境变量配置有问题: (base) xxxM73H-15:~/VueProject/pproject-vue$ npm run dev /usr/bin/env: “node”: 没有那个文件或目录vue项目启动有问题: (base) xxx:~/VueProject/pproj…...

电路元件与电路基本定理
电流、电压和电功率 电流 1 定义: 带电质点的有序运动形成电流 。 单位时间内通过导体横截面的电量定义为电流强度, 简称电流,用符号 i 表示,其数学表达式为:(i单位:安培(A&#x…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...
