《机器学习》——线性回归模型
文章目录
- 线性回归模型简介
- 一元线性回归模型
- 多元线性回归模型
- 误差项分析
- 一元线性模型实例
- 完整代码
- 多元线性模型实例
- 完整代码
线性回归模型简介
- 线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
- 相关关系:包含因果关系和平行关系
- 因果关系:回归分析【原因引起结果,需要明确自变量和因变量】
- 平行关系:相关关系【无因果关系,不区分自变量和因变量】
一元线性回归模型

多元线性回归模型

误差项分析
- 误差项满足高斯分布:




- 求解

- 一元线性回归模型与多元线性回归模型的区别
- 自变量数量:一元线性回归只涉及一个自变量,而多元线性回归涉及两个或更多自变量。
- 模型复杂度:由于包含更多的自变量,多元线性回归模型能够捕捉更复杂的数据关系,但也面临过拟合和变量选择等挑战。
- 解释性:在多元线性回归中,每个自变量的回归系数表示在保持其他自变量不变的情况下,该自变量每增加一个单位对因变量的平均影响。而在一元线性回归中,这个解释更为直接和简单。
- 应用场景:当数据集中只有一个自变量时,使用一元线性回归;当数据集包含多个可能相关的自变量时,使用多元线性回归。
一元线性模型实例
- 安装scikit-learn
python中执行线性回归的一个非常流行和强大的库是scikit-learn。scikit-learn提供了丰富的工具来进行数据挖掘和数据分析,包括简单和复杂的线性回归模型。
pip install scikit-learn
-
准备数据集

- 数据集文件:通过网盘分享的文件:data.csv
链接: https://pan.baidu.com/s/119pHKJu0ZPGYUfQA6_hYfg 提取码: i3vf
- 数据集文件:通过网盘分享的文件:data.csv
-
实例步骤
-
导入数据
-
绘制数据的散点图
-
求特征之间的相关系数
-
估计模型参数,建立回归模型
-
训练模型
-
测试模型
-
求出线性回归模型
- 导入数据
通过导入pandas模块,使用pandas的读取csv文件的方法进行导入数据集。
data = pd.read_csv('data.csv')- 绘制散点图
plt.scatter(data.广告投入,data.销售额) plt.show()
- 求特征之间的相关系数
在Python中,特别是在使用pandas库处理数据时,corr()函数是一个非常有用的方法,它用于计算DataFrame中列与列之间的相关系数。
相关系数越接近1,说明它们之间受相互的影响越大。corr = data.corr()
- 估计模型参数,建立回归模型
分别用变量接收数据中的值,后面传入模型中训练
这里直接调用 scikit-learn 库中的 LinearRegression() 模型lr = LinearRegression() x = data[["广告投入"]] y = data[["销售额"]]- 训练模型
使用sklearn模块中的fit()方法进行训练
lr.fit(x,y)- 测试模型
这里取两个例子进行测试预测,score()方法用于评估模型对给定数据(x, y)的拟合优度,其中x是自变量数据,y是真实的因变量数据。对于线性回归模型,score 方法默认计算的是决定系数(R2 score),它表示模型预测值与实际值之间的拟合程度。R2 score的值越接近1,说明模型的拟合效果越好;如果为0,则表示模型的表现和简单预测平均值一样;如果小于0,则表示模型的表现甚至不如简单预测平均值。
score = lr.score(x,y) # print(lr.predict([[50]])) print(lr.predict([[70]]))- 求出线性回归模型
分别求出回归的模型的截距和斜率,.coef_方法用来求斜率而.intercept_方法用来求截距
b = lr.coef_ c = lr.intercept_ print("一元线性回归模型为:y={:.2f}x1 + {:.2f}.".format(b[0][0],c[0]))- 结果

-
完整代码
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegressiondata = pd.read_csv('data.csv')
a = data.广告投入
# 绘制散点图
plt.scatter(data.广告投入,data.销售额)
plt.show()corr = data.corr()# 求x和y的相关系数
print(corr)
# 估计模型参数,建立回归模型
lr = LinearRegression()
x = data[["广告投入"]]
y = data[["销售额"]]lr.fit(x,y)# 训练模型score = lr.score(x,y)
#
print(lr.predict([[50]]))
print(lr.predict([[70]]))
b = lr.coef_
c = lr.intercept_
print("一元线性回归模型为:y={:.2f}x1 + {:.2f}.".format(b[0][0],c[0]))
多元线性模型实例
多元线性模型与一元线性模型结构差不多相同,有些许差别。
- 导入数据

本次使用的数据为糖尿病的数据,共有10个特征变量的自变量和最后一列的因变量。
通过网盘分享的文件:糖尿病数据.csv
链接: https://pan.baidu.com/s/1lO8IshYhgmkGlNYMBMIK4w 提取码: mh94
完整代码
import pandas as pd
from sklearn.linear_model import LinearRegressiondata = pd.read_csv("糖尿病数据.csv")corr = data[['age','sex','bmi','bp','s1','s2','s3','s4','s5','s6','target']].corr()lr_model = LinearRegression()
x = data[['age','sex','bmi','bp','s1','s2','s3','s4','s5','s6']]
y = data[['target']]lr_model.fit(x,y)score = lr_model.score(x,y)print(lr_model.predict([[-0.0926954778032799,-0.044641636506989,-0.0406959404999971,-0.0194420933298793,-0.0689906498720667,-0.0792878444118122,0.0412768238419757,-0.076394503750001,-0.0411803851880079,-0.0963461565416647]]))
print(lr_model.predict([[-0.0963280162542995,-0.044641636506989,-0.0838084234552331,0.0081008722200108,-0.103389471327095,-0.0905611890362353,-0.0139477432193303,-0.076394503750001,-0.0629129499162512,-0.0342145528191441]]))a = lr_model.coef_
b = lr_model.intercept_print("糖尿病线性回归模型为:y ={:.2f}x1 + {:.2f}x2 + {:.2f}x3 + {:.2f}x4 + {:.2f}x5 + {:.2f}x6 + {:.2f}x7 + {:.2f}x8 + {:.2f}x9 + {:.2f}x10 + {:.2f}.".format(a[0][0],a[0][1],a[0][2],a[0][3],a[0][4],a[0][5],a[0][6],a[0][7],a[0][8],a[0][9],b[0]))
- 结果

可以看到一元线性回归模型和多元线性回归模型的结果只是多元线性回归模型有多个自变量,来控制因变量,且多元线性回归模型要导入多个特征数据,数据处理阶段并无太大区别。
相关文章:

《机器学习》——线性回归模型
文章目录 线性回归模型简介一元线性回归模型多元线性回归模型误差项分析一元线性模型实例完整代码 多元线性模型实例完整代码 线性回归模型简介 线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。 相关关系&…...
网卡信息没有了问题处理)
Linux(Centos 7.6)网卡信息没有了问题处理
1.问题现象 虚拟机打开后,使用ifconfig查看IP信息,虚拟机默认的网卡名称是ens33,ifconfig没有看到相关问题,远程连接工具Xshell也不能正常访问该虚拟机。 [rootnode1 ~]# ifconfig lo: flags73<UP,LOOPBACK,RUNNING> mtu…...

WEB攻防-通用漏洞-文件上传-js验证-MIME验证-user.ini-语言特征
目录 定义 1.前端验证 2.MIME验证 3.htaccess文件和.user. ini 4.对内容进行了过滤,做了内容检测 5.[ ]符号过滤 6.内容检测php [] {} ; 7.()也被过滤了 8.反引号也被过滤 9.文件头检测 定义 文件上传漏洞是指攻击者上传了一个可执行文件(如木马…...

mybatis-plus代码生成器
<!--mybatis-plus--><dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus-boot-starter</artifactId><version>3.5.2</version></dependency><!--mybatis-plus-generator 生成器--><depende…...

12.24-12.28Mysql锁阅读笔记
1.Mysql的锁有哪些种类 全局锁, 通过flush tables with read lock 应用场景是全局备份,备份的时候如果有两个表,备份 先备份了用户表,然后用户了商品,再备份商品表 那么商品表库存减少了,然而用户表的育儿…...

支持最新 mysql9的workbench8.0.39 中文汉化教程来了
之前在 B 站上发布了 mysql8 workbench 汉化教程,一年多来帮助很多初学者解决了不熟悉英文的烦恼。 汉化视频可以访问: 2024最新版mysql8.0.39中文版mysql workbench汉化 中文升级 旧版汉化报错解决_哔哩哔哩_bilibili MySql Workbench汉化_哔哩哔哩_…...

golang连接jenkins构建build
1.安装jenkins依赖 go get github.com/bndr/gojenkins2.代码 import ("context""file/utils/logs""github.com/bndr/gojenkins""github.com/gin-gonic/gin""net/http""time" )// 接收单个静态文件上线参数 type…...
)
SCAU高程进阶题(自用)
18711 字符串去重 Description 一个完全由小写字母组成的长度为n的字符串,现在要求你去除所有重复的字母,并将剩下的字母按从小到大的次序输出。 如输入baaadccaab,输出abcd。 输入格式 第一行一个整数n,表示字符串长度(0<n&…...

基于STM32F103控制L298N驱动两相四线步进电机
文章目录 前言一、模块参数二、接口说明三、准备工作四、直流电机驱动引脚接线效果展示 五、两相四线步进电机驱动步进电机相关概念拍数驱动时序引脚接线效果展示 六、参考示例 前言 L298N 是一种常见的双 H 桥电机驱动模块,广泛用于驱动直流电机和步进电机。它基于…...

libreoffice在Windows和Linux环境的安装和结合Springboot使用教程
前言: 在公司做开发时,遇到一个需求,要求上传的文件有图片,也有word和pdf。预览信息时,既要求能水印展示出来,又要求能大图水印预览。思索许久,我决定采取全部打水印然后转成图片Base64&#x…...

前端开发 -- 自动回复机器人【附完整源码】
一:效果展示 本项目实现了一个简单的网页聊天界面,用户可以在输入框中输入消息,并点击发送按钮或按下回车键来发送消息。机器人会根据用户发送的消息内容,通过关键字匹配来生成自动回复。 二:源代码分享 <!DOCTYP…...
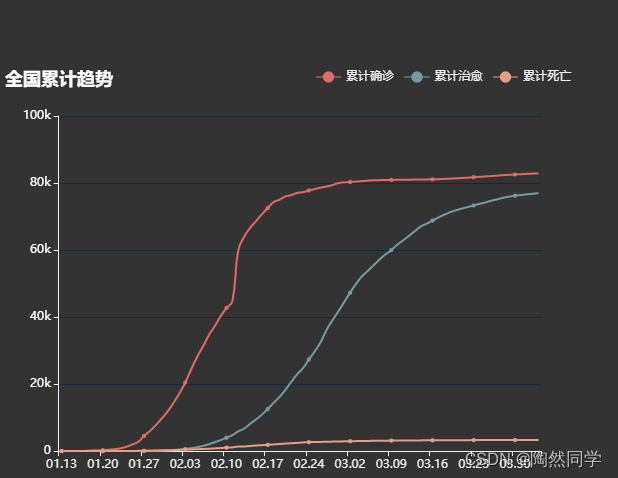
vue+echarts实现疫情折线图
效果: 代码: <<template><div><div id"left1" style "height:800px;width:100%"></div></div> </template><script> //疫情数据//export default {data() {return {data:{//疫情数据…...

服务器nfs文件共享
1. 配置 NFS 服务器(NFS Server) 在 Ubuntu/Debian 上: sudo apt update sudo apt install nfs-kernel-server在 CentOS/RHEL 上: sudo yum install nfs-utils1.2 创建共享目录 选择一个要共享的目录,并确保该目录的权限正确设置。例如,假设我们要共享 /srv/nfs 目录…...
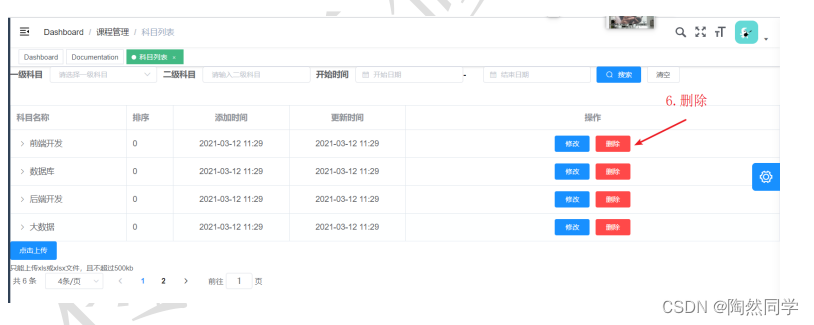
基于Vue+SSM+SpringCloudAlibaba的科目课程管理系统
功能1:科目列表 功能2:条件查询 功能3:分页查询 功能4:excel批量导入 功能5:修改 功能6:删除...

vue3配置caddy作为静态服务器,在浏览器地址栏刷新出现404
vue3配置caddy作为静态服务器,在浏览器地址栏刷新出现404 1 情况描述2 原因3 配置 1 情况描述 在vue打包之后,形成dist文件,采用caddy作为静态资源服务器。在浏览器中输入域名时可以访问网站,但是,进过路由导航栏内部…...

深入理解委托:C# 编程中的强大工具
在面向对象编程中,委托(Delegate) 是一个非常强大且灵活的概念,特别是在 C# 编程语言中。它不仅仅是函数指针的替代品,还提供了更高层次的抽象,使得代码更加简洁、灵活和可维护。在这篇博客中,我…...
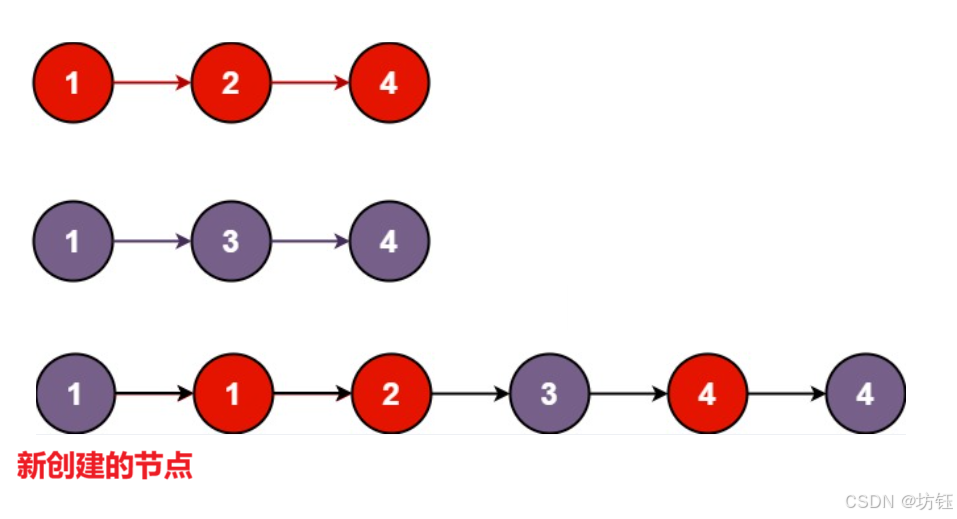
【Java 数据结构】合并两个有序链表
🔥博客主页🔥:【 坊钰_CSDN博客 】 欢迎各位点赞👍评论✍收藏⭐ 目录 1. 题目 2. 解析 3. 代码实现 4. 小结 1. 题目 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 示…...
基于微信小程序的校园访客登记系统
基于微信小程序的校园访客登记系统 功能列表 用户端功能 注册与登录 :支持用户通过手机号短信验证码注册和登录。个人资料管理 :允许用户编辑和更新个人信息及其密码。站内信消息通知:通知公告。来访预约:提交来访预约支持车牌…...
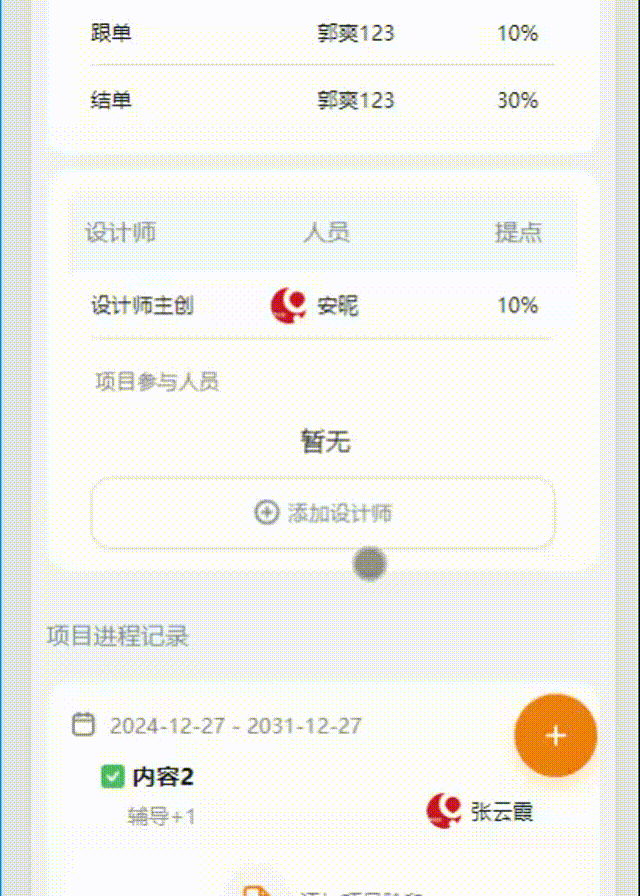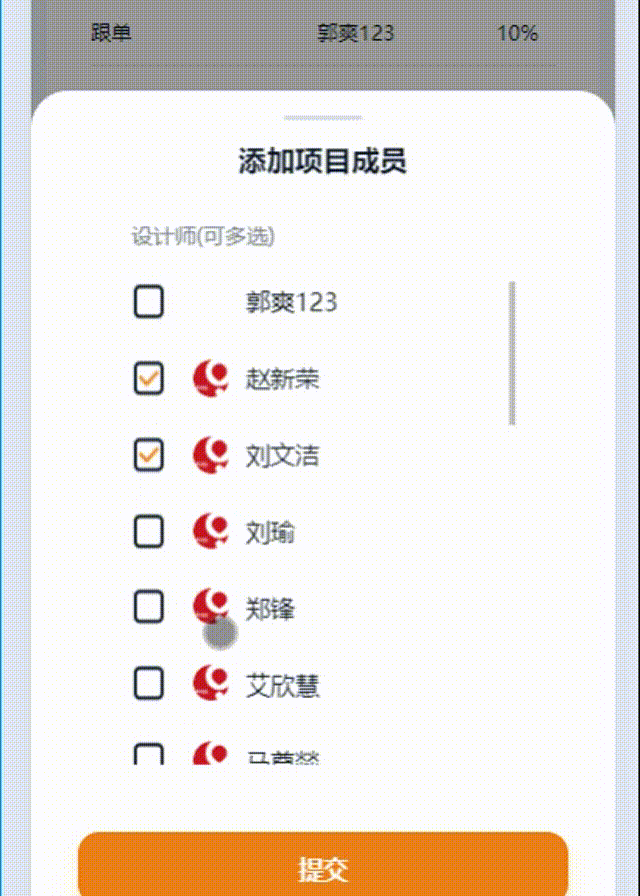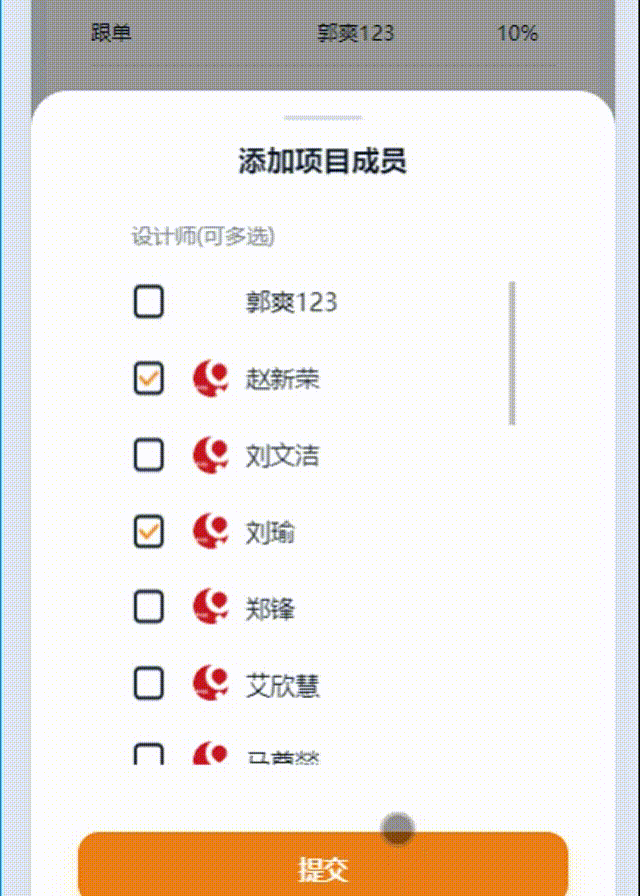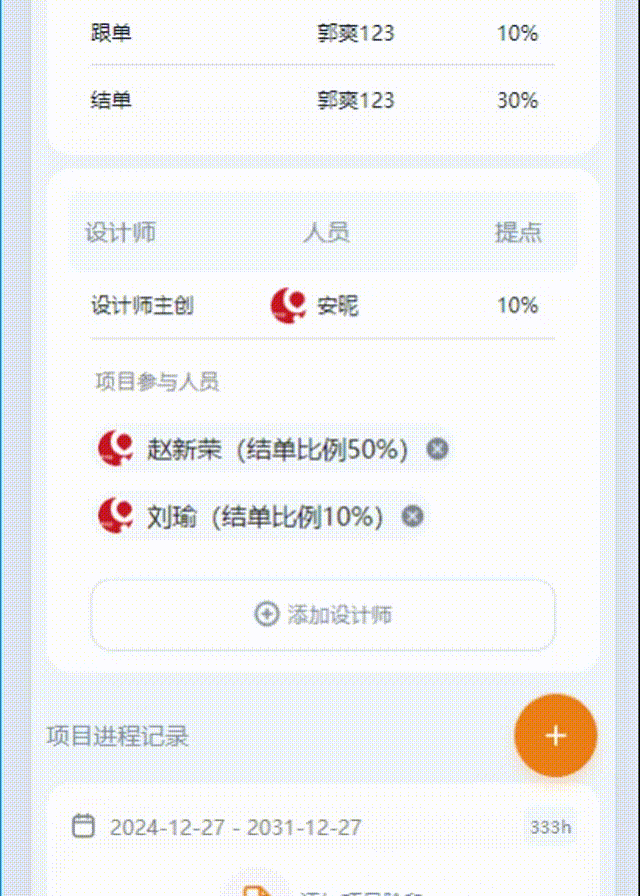
uniapp 判断多选、选中取消选中的逻辑处理
一、效果展示 二、代码 1.父组件: :id=“this.id” : 给子组件传递参数【id】 @callParentMethod=“takeIndexFun” :给子组件传递方法,这样可以在子组件直接调用父组件的方法 <view @click="$refs.member.open()"...

php8.0版本更新了哪些内容
PHP 8.0版本是PHP语言的一个重要更新,它引入了许多新特性和改进,旨在提高性能、增强代码的可读性和可维护性。以下是PHP 8.0版本更新的主要内容: 一、性能提升 JIT编译器:PHP 8.0引入了Just-In-Time(JIT)…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...

Django RBAC项目后端实战 - 03 DRF权限控制实现
项目背景 在上一篇文章中,我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统,为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...

【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...

Java中HashMap底层原理深度解析:从数据结构到红黑树优化
一、HashMap概述与核心特性 HashMap作为Java集合框架中最常用的数据结构之一,是基于哈希表的Map接口非同步实现。它允许使用null键和null值(但只能有一个null键),并且不保证映射顺序的恒久不变。与Hashtable相比,Hash…...

【阅读笔记】MemOS: 大语言模型内存增强生成操作系统
核心速览 研究背景 研究问题:这篇文章要解决的问题是当前大型语言模型(LLMs)在处理内存方面的局限性。LLMs虽然在语言感知和生成方面表现出色,但缺乏统一的、结构化的内存架构。现有的方法如检索增强生成(RA…...
