【漫话机器学习系列】029.累积分布函数(Cumulative Distribution Function)

累积分布函数(Cumulative Distribution Function, CDF)
累积分布函数(CDF)是概率论和统计学中的一个基本概念,用于描述随机变量取值的累积概率分布情况。它在理论研究和实际应用中广泛使用。
定义
给定随机变量 X,其累积分布函数 F(x) 定义为:
说明
- F(x):表示随机变量 X 的值小于或等于某个值 x 的概率。
- P:表示概率。
性质
- 单调不减性:
,当
时。
- 取值范围:
。
- 极限性质:
- 连续性:对于连续型随机变量,F(x) 是连续函数;对于离散型随机变量,F(x) 是阶梯函数。
类型
-
连续型随机变量:
其中,f(x) 是概率密度函数(PDF)。
-
离散型随机变量:
其中,
是随机变量在离散点
的概率。
图示
累积分布函数通常表现为一个逐步上升或连续上升的曲线,随着 x 的增加,曲线趋向于 1。
- 离散型随机变量:阶梯状。
- 连续型随机变量:平滑曲线。
示例
1. 离散型随机变量
假设 X 为投掷一个骰子的点数,其可能值为 1, 2, 3, 4, 5, 6,每个值的概率为 。累积分布函数为:
2. 连续型随机变量
假设 X 服从标准正态分布,其概率密度函数为:
其累积分布函数为:
由于无法用初等函数表示,通常使用数值积分或标准正态分布表计算。
Python 实现
1. 连续型随机变量
使用 SciPy 计算正态分布的累积分布函数:
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt# 定义随机变量
x = np.linspace(-4, 4, 1000)
# 标准正态分布的CDF
cdf = norm.cdf(x)# 绘图
plt.plot(x, cdf, label='CDF of Standard Normal Distribution')
plt.xlabel('x')
plt.ylabel('F(x)')
plt.title('Cumulative Distribution Function')
plt.grid()
plt.legend()
plt.show()
运行结果

plt.legend() plt.show()
2. 离散型随机变量
计算骰子点数的累积分布函数:
import numpy as np
import matplotlib.pyplot as plt# 假设 x 是 [1, 2, 3, 4, 5, 6]
x = np.arange(1, 7)
cdf = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6]) # 示例 CDF 数据# 调整 y 的长度以匹配 x
y_adjusted = np.concatenate(([0], cdf))[:-1]plt.step(x, y_adjusted, where='post', label='CDF of Dice')
plt.legend()
plt.show()运行结果

应用
- 概率计算:通过 F(x),可以快速计算任意区间内的概率:
- 随机数生成:通过反向变换法生成符合特定分布的随机数。
- 统计分析:用于描述数据分布及模型拟合效果。
总结
累积分布函数是随机变量概率分布的重要工具,能够直观地描述随机变量的累积概率分布。通过 CDF,既可以快速计算概率,又能用于随机数生成和分布分析。无论是离散型还是连续型随机变量,CDF 都在理论研究和实际应用中扮演着重要角色。
相关文章:
【漫话机器学习系列】029.累积分布函数(Cumulative Distribution Function)
累积分布函数(Cumulative Distribution Function, CDF) 累积分布函数(CDF)是概率论和统计学中的一个基本概念,用于描述随机变量取值的累积概率分布情况。它在理论研究和实际应用中广泛使用。 定义 给定随机变量 X&am…...

设计模式之访问者模式:一楼千面 各有玄机
~犬📰余~ “我欲贱而贵,愚而智,贫而富,可乎? 曰:其唯学乎” 一、访问者模式概述 \quad 江湖中有一个传说:在遥远的东方,有一座神秘的玉楼。每当武林中人来访,楼中的各个房…...

AI 编程的世界:用Cursor编写评分项目
AI 编程的世界:用Cursor编写评分项目 今天是2024年的最后一天,祝大家在新的一年,健康开心快乐! 岁末之际,星辰为伴,灯火长明,我终于在 2024 年的最后一天成功上线了 AI 编程项目。回首这一年&am…...
Cesium教程(二十三):Cesium实现下雨场景
文章目录 实现效果代码引入js文件创建容器创建视图定义下雨场景完整代码下载实现效果 代码 在 Cesium 中利用PostProcessStageLibrary实现下雪场景,你可以按照以下步骤进行: 创建一个 PostProcessStage:首先,你需要创建一个PostProcessStage对象,它将用于定义下雪效果的渲…...
SpringCloudAlibaba技术栈-Higress
1、什么是Higress? 云原生网关,干啥的?用通俗易懂的话来说,微服务架构下Higress 就像是一个智能的“交通警察”,它站在你的网络世界里,负责指挥和调度所有进出的“车辆”(也就是数据流量)。它的…...

uniapp 微信小程序开发使用高德地图、腾讯地图
一、高德地图 1.注册高德地图开放平台账号 (1)创建应用 这个key 第3步骤,配置到项目中locationGps.js 2.下载高德地图微信小程序插件 (1)下载地址 高德地图API | 微信小程序插件 (2)引入项目…...
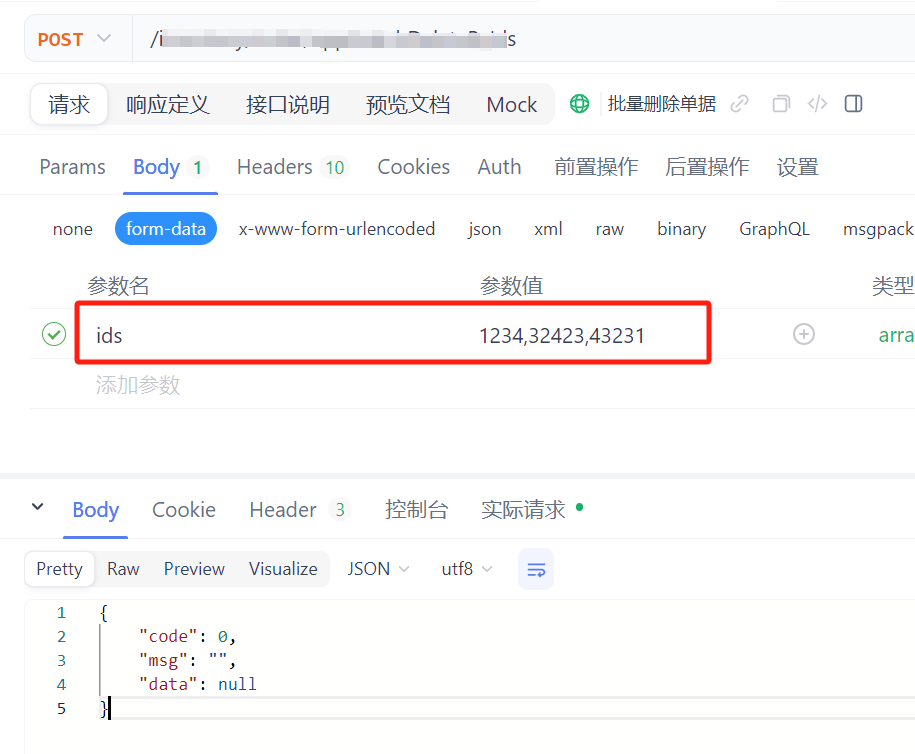
Springboot:后端接收数组形式参数
1、接收端写法 PermissionAnnotation(permissionName "",isCheckToken true)PostMapping("/batchDeleteByIds")public ReturnBean webPageSelf( NotNull(message "请选择要删除的单据!") Long[] ids) {for (Long string : ids) {l…...
Postman[2] 入门——界面介绍
可参考官方 文档 Postman 导航 | Postman 官方帮助文档中文版Postman 拥有各种工具、视图和控件,帮助你管理 API 项目。本指南是对 Postman 主要界面区域的高级概述:https://postman.xiniushu.com/docs/getting-started/navigating-postman 1. Header&a…...

1月第四讲:Java Web学生自习管理系统
一、项目背景与需求分析 随着网络技术的不断发展和学校规模的扩大,学生自习管理系统的需求日益增加。传统的自习管理方式存在效率低下、资源浪费等问题,因此,开发一个智能化的学生自习管理系统显得尤为重要。该系统旨在提高自习室的利用率和…...

【Redis】Redis 典型应用 - 缓存 (cache)
目录 1. 什么是缓存 2. 使用 Redis 作为缓存 3. 缓存的更新策略 3.1 定期生成 3.2 实时生成 4. 缓存的淘汰策略 5. 缓存预热, 缓存穿透, 缓存雪崩 和 缓存击穿 关于缓存预热 (Cache preheating) 关于缓存穿透 (Cache penetration) 关于缓存雪崩 (Cache avalanche) 关…...
HTML——38.Span标签和字符实体
<!DOCTYPE html> <html><head><meta charset"UTF-8"><title>span标签和字符实体</title><style type"text/css">h1{text-align: center;}p{text-indent: 2em;}span{color: red;}</style></head><…...

ROS2+OpenCV综合应用--10. AprilTag标签码追踪
1. 简介 apriltag标签码追踪是在apriltag标签码识别的基础上,增加了小车摄像头云台运动的功能,摄像头会保持标签码在视觉中间而运动,根据这一特性,从而实现标签码追踪功能。 2. 启动 2.1 程序启动前的准备 本次apriltag标签码使…...

python Celery 是一个基于分布式消息传递的异步任务队列系统
Celery 是一个基于分布式消息传递的异步任务队列系统,主要用于处理耗时任务、定时任务和周期性任务。它能够将任务分配到多个工作节点(Worker)上执行,从而提高应用程序的性能和可扩展性。Celery 是 Python 生态中最流行的任务队列…...
嵌入式硬件杂谈(七)IGBT MOS管 三极管应用场景与区别
引言:在现代嵌入式硬件设计中,开关元件作为电路中的重要组成部分,起着至关重要的作用。三种主要的开关元件——IGBT(绝缘栅双极型晶体管)、MOSFET(金属氧化物半导体场效应晶体管)和三极管&#…...

麒麟信安云在长沙某银行的应用入选“云建设与应用领航计划(2024)”,打造湖湘金融云化升级优质范本
12月26日,2024云计算产业和标准应用大会在北京成功召开。大会汇集政产学研用各方专家学者,共同探讨云计算产业发展方向和未来机遇,展示云计算标准化工作重要成果。 会上,云建设与应用领航计划(2024)建云用…...

好用的随机生成图片的网站
官网: Lorem Picsum 获取自定义大小的随机图像 https://picsum.photos/200/300 获取正方形图像 https://picsum.photos/200 获取特定类型的图像 通过添加到 /id/{image} url 的开头来获取特定图像。 https://picsum.photos/id/237/200/300 获取静态随机图像…...

添加 env 配置,解决import路径问题
添加 env 配置,解决import路径问题 { // 使用 IntelliSense 了解相关属性。 // 悬停以查看现有属性的描述。 // 欲了解更多信息,请访问: https://go.microsoft.com/fwlink/?linkid830387 “version”: “0.2.0”, “configurations”: [ {"name&q…...

Go work stealing 机制
Go语言的Work Stealing(工作窃取)机制是一种用于调度Goroutines(协程)的策略,其核心目的是最大化CPU使用率,减少任务调度的开销,并提高并发性能和吞吐量。以下是Go Work Stealing机制的详细解释…...

基础数据结构--二叉树
一、二叉树的定义 二叉树是 n( n > 0 ) 个结点组成的有限集合,这个集合要么是空集(当 n 等于 0 时),要么是由一个根结点和两棵互不相交的二叉树组成。其中这两棵互不相交的二叉树被称为根结点的左子树和右子树。 如图所示&am…...

《C++设计模式》策略模式
文章目录 1、引言1.1 什么是策略模式1.2 策略模式的应用场景1.3 本文结构概览 2、策略模式的基本概念2.1 定义与结构2.2 核心角色解析2.2.1 策略接口(Strategy)2.2.2 具体策略实现(ConcreteStrategy)2.2.3 上下文(Cont…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
