论文实现:Reactive Nonholonomic Trajectory Generation via Parametric Optimal Control
1. 多项式螺旋
曲率:
κ ( s ) = a 0 + a 1 s + a 2 s 2 + a 3 s 3 + a 4 s 4 + a 5 s 5 \begin{align} \kappa(s) = a_0 + a_1s + a_2s^2 + a_3s^3 + a_4s^4 + a_5s^5 \end{align} κ(s)=a0+a1s+a2s2+a3s3+a4s4+a5s5
机器人朝向:
θ ( s ) = a 0 s + a 1 s 2 2 + a 2 s 3 3 + a 3 s 4 4 + a 4 s 5 5 + a 5 s 6 6 \begin{align} \theta(s) = a_0s + \frac{a_1s^2}{2} + \frac{a_2s^3}{3} + \frac{a_3s^4}{4} + \frac{a_4s^5}{5} + \frac{a_5s^6}{6} \end{align} θ(s)=a0s+2a1s2+3a2s3+4a3s4+5a4s5+6a5s6
轨迹:
x ( s ) = ∫ 0 s cos ( θ ( s ) ) d s \begin{align} x(s) = \int_0^s{\cos(\theta(s))ds} \end{align} x(s)=∫0scos(θ(s))ds
y ( s ) = ∫ 0 s sin ( θ ( s ) ) d s \begin{align} y(s) = \int_0^s{\sin(\theta(s))ds} \end{align} y(s)=∫0ssin(θ(s))ds
2. 边界条件
初始条件: s = 0 , x = 0 , y = 0 , θ = 0 s = 0,x = 0, y = 0, \theta = 0 s=0,x=0,y=0,θ=0
结束条件: s = s f , x = x f , y = y f , θ = θ f s = s_f, x = x_f, y = y_f, \theta = \theta_f s=sf,x=xf,y=yf,θ=θf
x b = [ x f y f θ f ] T \begin{align} \bf{x_b} = \left[ x_f \ y_f \ \theta_f \right]^T \end{align} xb=[xf yf θf]T
参数:
q = [ a 0 a 1 a 2 a 3 a 4 a 5 s f ] T \begin{align} \bf{q} = \left[a_0 \ a_1 \ a_2 \ a_3 \ a_4 \ a_5 \ s_f \right]^T \end{align} q=[a0 a1 a2 a3 a4 a5 sf]T
边界条件:
g ( q ) = h ( q ) − x b = { x ( s f ) − x f = 0 y ( s f ) − y f = 0 θ ( s f ) − θ f = 0 \begin{align} \bf{g(q)} = \bf{h(q)} - \bf{x_b} = \begin{cases} x(s_f) - x_f = 0 \\ y(s_f) - y_f = 0 \\ \theta(s_f) - \theta_f = 0 \end{cases} \end{align} g(q)=h(q)−xb=⎩ ⎨ ⎧x(sf)−xf=0y(sf)−yf=0θ(sf)−θf=0
待续…
相关文章:

论文实现:Reactive Nonholonomic Trajectory Generation via Parametric Optimal Control
1. 多项式螺旋 曲率: κ ( s ) a 0 a 1 s a 2 s 2 a 3 s 3 a 4 s 4 a 5 s 5 \begin{align} \kappa(s) a_0 a_1s a_2s^2 a_3s^3 a_4s^4 a_5s^5 \end{align} κ(s)a0a1sa2s2a3s3a4s4a5s5 机器人朝向: θ ( s ) a 0 s a 1 …...

基于单片机中药存放环境监测系统的实现
基于单片机中药存放环境监测系统的实现 项目开发背景 随着现代中药的广泛应用,中药材的存储环境对其质量有着至关重要的影响。温湿度、烟雾、火灾等环境因素,若不加以控制,将会导致中药材失效或变质。因此,设计一个基于单片机的…...

九垠赢+商业管理系统 Common.ashx 文件上传致RCE漏洞复现
0x01 产品简介 九垠赢+商业管理系统是基于互联网技术的进销存管理软件,适用于新零售背景下各种业态的线上线下一体化的商超经营管理。赢+ERP以商业管理系统为底座,融合了多种软、硬件解决方案,实现了从企业、供应商、三方平台到顾客等日常管理的全线数字化、智能化和移动化…...

速盾:服务器CDN加速解析的好处有哪些呢?
随着互联网应用的普及,越来越多的企业开始关注如何提升网站的访问速度和用户体验。为了实现这一目标,许多企业选择使用CDN(内容分发网络)来加速网站的内容分发。CDN通过在全球范围内分布多个节点,将内容缓存到离用户最…...
)
C++ 设计模式:备忘录模式(Memento Pattern)
链接:C 设计模式 链接:C 设计模式 - 状态模式 备忘录模式(Memento Pattern)是一种行为设计模式,它允许在不破坏封装性的前提下捕获和恢复对象的内部状态。这个模式在需要保存和恢复对象状态的场景中非常有用ÿ…...

Android 系统 Activity 系统层深度定制的方法、常见问题以及解决办法
Android 系统 Activity 系统层深度定制的方法、常见问题以及解决办法 目录 引言Activity 系统层概述Activity 系统架构图Activity 系统层深度定制的方法 4.1 自定义 Activity 生命周期4.2 自定义 Activity 启动流程4.3 自定义 Activity 转场动画4.4 自定义 Activity 窗口管理4…...

PDF怎么压缩得又小又清晰?5种PDF压缩方法
PDF 文件在日常办公与学习中使用极为频繁,可想要把它压缩得又小又清晰却困难重重。一方面,PDF 格式本身具有高度兼容性,集成了文字、图像、矢量图等多样元素,压缩时难以兼顾不同元素特性,稍不注意,文字就会…...

YK人工智能(三)——万字长文学会torch深度学习
2.1 张量 本节主要内容: 张量的简介PyTorch如何创建张量PyTorch中张量的操作PyTorch中张量的广播机制 2.1.1 简介 几何代数中定义的张量是基于向量和矩阵的推广,比如我们可以将标量视为零阶张量,矢量可以视为一阶张量,矩阵就是…...

关于CISP报名费用详情
CISP即“注册信息安全专业人员”,是中国信息安全测评中心实施的国家认证项目,旨在培养信息安全领域的专业人才。对于有意报考CISP的考生而言,了解报名考试费用是备考过程中不可或缺的一环。 CISP的报名考试费用主要包括培训费用、考试费用、…...

vim 按下esc后取消高亮
配置 ideavimrc文件 " 按下 Esc 键时自动取消高亮 " 在普通模式下按下 Esc 键取消高亮 nnoremap <Esc> :nohlsearch<CR> " 在插入模式下按下 Esc 键取消高亮 inoremap <Esc> <Esc>:nohlsearch<CR>" 额外:当退出…...

SwiftUI:多语言实现富文本插值
实现的UI需求: 要求: 英文显示:3068 people have joined this plan today! 中文显示:今日有 3068 人已加入此计划! 实现代码: Text(AttributedString(localized:"**\(payPeoples)** people have joi…...

操作系统基础
概念 控制和管理操作系统软件和硬件 用户观点:用户和计算机之间的接口 基本概念 特征 并发,共享,虚拟,异步 功能 处理机管理,存储器管理,文件管理,设备管理 作为用户和硬件接口 命令接口&am…...

函数调用流程可用工具
方法 1、gdb,这个网上很多找找就有 2、tcmalloc,直接在调用的地方调一个malloc就可以看到调用的流程,具体见tcmalloc 3、backtrace,个人感觉这么最方便,具体见backtrace...

UniApp 页面布局基础
一、UniApp 页面布局简介 在当今的移动应用开发领域,跨平台开发已成为一种主流趋势。UniApp作为一款极具影响力的跨平台开发框架,凭借其“一套代码,多端运行”的特性,为开发者们提供了极大的便利,显著提升了开发效率。…...
2D图像测量到3D点云之物体三维尺寸测量!!!!
0,引言 本文将从双目采集的2D图像到3D点云进行转化,并进行物体尺寸测量,旨在为读者展示2D图像如何关联3D点云,并进行相关工业应用。 将2D图像转化为3D点云,并进行物体尺寸测量的技术,在工业领域有着广泛的…...
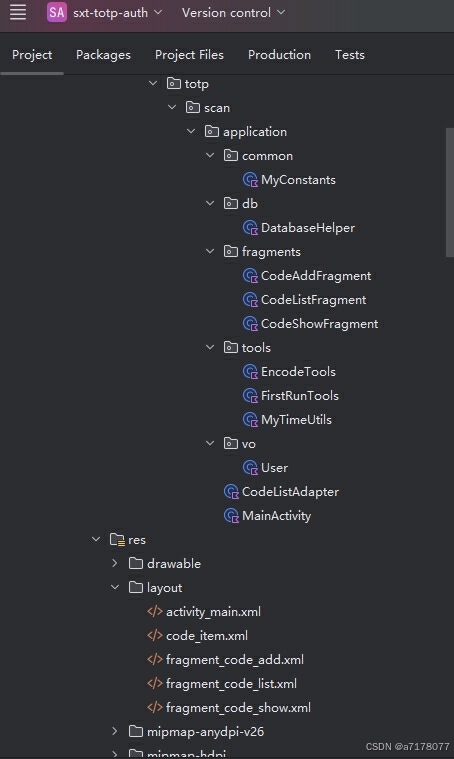
[TOTP]android kotlin实现 totp身份验证器 类似Google身份验证器
背景:自己或者公司用一些谷歌身份验证器或者microsoft身份验证器,下载来源不明,或者有广告,使用不安全。于是自己写一个,安全放心使用。 代码已开源:shixiaotian/sxt-android-totp: android totp authenti…...
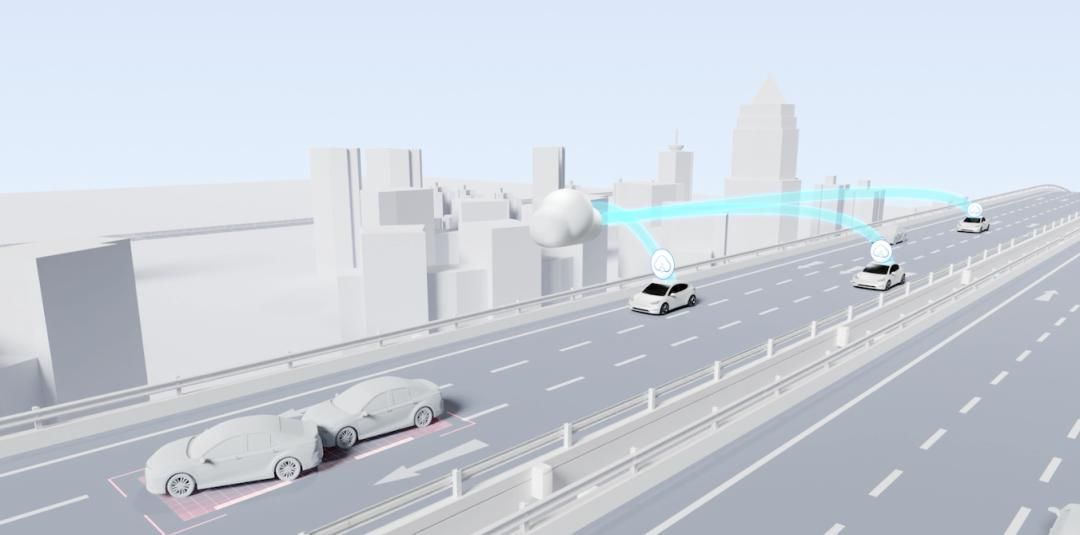
2025决战智驾:从中阶卷到L3,车企需要抓好一个数据闭环
作者 |王博 编辑 |德新 全国都能开之后,智驾继续走向哪里? 2024年末,大部分主流车企已经实现了无(高精度)图全国都能开。而第一梯队的玩家,从以规则为主的算法框架,向神经网络模型为主的新架构…...

电子电气架构 --- 汽车电子电器设计概述
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 所谓鸡汤,要么蛊惑你认命,要么怂恿你拼命,但都是回避问题的根源,以现象替代逻辑,以情绪代替思考,把消极接受现实的懦弱,伪装成乐观面对不幸的…...
SpringAI从入门到熟练
学习SpringAI的记录情况 文章目录 前言 因公司需要故而学习SpringAI文档,故将自己所见所想写成文章,供大佬们参考 主要是为什么这么写呢,为何不抽出来呢,还是希望可以用的时候更加方便一点,如果大家有需求可以自行去…...

[算法] [leetcode-20] 有效的括号
20 有效的括号 给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。 有效字符串需满足: 左括号必须用相同类型的右括号闭合。 左括号必须以正确的顺序闭合…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...
