人工智能知识分享第四天-线性回归
线性回归
线性回归介绍
线性回归概念
- 线性回归(Linear regression)是利用 回归方程(函数) 对 一个或多个自变量(特征值)和因变量(目标值)之间 关系进行建模的一种分析方式。

注意事项:
1 为什么叫线性模型?因为求解的w,都是w的零次幂(常数项)所以叫成线性模型
2 在线性回归中,从数据中获取的规律其实就是学习权重系数w
3 某一个权重值w越大,说明这个权重的数据对房子价格影响越大
线性回归分类
-
一元线性回归
y = kx +b
目标值只与一个因变量有关系 -
多元线性回归

线性回归问题的求解
预测6号体重
已知数据:

需求:6号身高是176,请预测体重?

损失函数
需要设置一个评判标准
误差概念:用预测值y – 真实值y就是误差
损失函数:衡量每个样本预测值与真实值效果的函数
“红色直线能更好的拟合所有点”也就是误差最小,误差和最小
损失函数数学如何表达呢?又如何求损失函数的最小值呢?



当损失函数取最小值时,得到k就是最优解



想求一条直线更好的拟合所有点 y = kx + b
-
引入损失函数(衡量预测值和真实值效果) Loss(k, b)
-
通过一个优化方法,求损失函数最小值,得到K最优解
-

-
回归的损失函数:
-
均方误差 (Mean-Square Error, MSE)
-

-
平均绝对误差 (Mean Absolute Error , MAE)
-


多元线性回归的解析解-正规方程法


梯度下降算法
梯度下降算法思想
什么是梯度下降法
• 求解函数极值还有更通用的方法就是梯度下降法。顾名思义:沿着梯度下降的方向求解极小值 • 举个例子:坡度最陡下山法

- 输入:初始化位置S;每步距离为a 。输出:从位置S到达山底
- 步骤1:令初始化位置为山的任意位置S
- 步骤2:在当前位置环顾四周,如果四周都比S高返回S;否则执行步骤3
- 步骤3: 在当前位置环顾四周,寻找坡度最陡的方向,令其为x方向
- 步骤4:沿着x方向往下走,长度为a,到达新的位置S‘
- 步骤5:在S‘位置环顾四周,如果四周都比S‘高,则返回S‘。否则转到步骤3
小结:通过循环迭代的方法不断更新位置S (相当于不断更新权重参数w)
最终找到最优解 这个方法可用来求损失函数最优解, 比正规方程更通用
梯度下降过程就和下山场景类似
可微分的损失函数,代表着一座山
寻找的函数的最小值,也就是山底

正规方程和梯度下降算法的对比

回归评估方法
为什么要进行线性回归模型的评估
我们希望衡量预测值和真实值之间的差距,
会用到MAE、MSE、RMSE多种测评函数进行评价
平均绝对误差
Mean Absolute Error (MAE)

- 上面的公式中:n 为样本数量, y 为实际值, y ^ \hat{y} y^ 为预测值
- MAE 越小模型预测约准确
Sklearn 中MAE的API
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test,y_predict)
均方误差
Mean Squared Error (MSE)

- 上面的公式中:n 为样本数量, y 为实际值, y ^ \hat{y} y^ 为预测值
- MSE 越小模型预测约准确
Sklearn 中MSE的API
from sklearn.metrics import mean_squared_error
mean_squared_error(y_test,y_predict)
均方根误差
Root Mean Squared Error (RMSE)

- 上面的公式中:n 为样本数量, y 为实际值, y ^ \hat{y} y^ 为预测值
- RMSE 越小模型预测约准确
三种指标的比较
我们绘制了一条直线 y = 2x +5 用来拟合 y = 2x + 5 + e. 这些数据点,其中e为噪声

从上图中我们发现 MAE 和 RMSE 非常接近,都表明模型的误差很低(MAE 或 RMSE 越小,误差越小!)。 但是MAE 和 RMSE 有什么区别?为什么MAE较低?
-
对比MAE 和 RMSE的公式,RMSE的计算公式中有一个平方项,因此:大的误差将被平方,因此会增加 RMSE 的值
-
可以得出结论,RMSE 会放大预测误差较大的样本对结果的影响,而 MAE 只是给出了平均误差
-
由于 RMSE 对误差的 平方和求平均 再开根号,大多数情况下RMSE>MAE
举例 (1+3)/2 = 2 ( 1 2 + 3 2 ) / 2 = 10 / 2 = 5 = 2.236 \sqrt{(1^2+3^2)/2 }= \sqrt{10/2} = \sqrt{5} = 2.236 (12+32)/2=10/2=5=2.236
我们再看下一个例子

橙色线与第一张图中的直线一样:y = 2x +5
蓝色的点为: y = y + sin(x)*exp(x/20) + e 其中 exp() 表示指数函数
我们看到对比第一张图,所有的指标都变大了,RMSE 几乎是 MAE 值的两倍,因为它对预测误差较大的点比较敏感
我们是否可以得出结论: RMSE是更好的指标? 某些情况下MAE更有优势,例如:
- 假设数据中有少数异常点偏差很大,如果此时根据 RMSE 选择线性回归模型,可能会选出过拟合的模型来
- 在这种情况下,由于数据中的异常点极少,选择具有最低 MAE 的回归模型可能更合适
- 除此之外,当两个模型计算RMSE时数据量不一致,也不适合在一起比较
今天先分享到这里
坚持分享 共同进步
相关文章:

人工智能知识分享第四天-线性回归
线性回归 线性回归介绍 线性回归概念 线性回归(Linear regression)是利用 回归方程(函数) 对 一个或多个自变量(特征值)和因变量(目标值)之间 关系进行建模的一种分析方式。 注意事项: 1 为什么叫线性模型?因为求解的w,都是w的零次幂&am…...

Appium 2.0:移动自动化测试的革新之旅
关注开源优测不迷路 大数据测试过程、策略及挑战 测试框架原理,构建成功的基石 在自动化测试工作之前,你应该知道的10条建议 在自动化测试中,重要的不是工具 在移动应用开发的领域中,Appium 作为一款强大的自动化测试工具…...

牛客网最新1129道 Java 面试题及答案整理
前言 面试,跳槽,每天都在发生,而对程序员来说"金三银四"更是面试和跳槽的高峰期,跳槽,更是很常见的,对于每个人来说,跳槽的意义也各不相同,可能是一个人更向往一个更大的…...
:自定义 Publisher 和 Subscriber)
Swift Combine 学习(六):自定义 Publisher 和 Subscriber
Swift Combine 学习(一):Combine 初印象Swift Combine 学习(二):发布者 PublisherSwift Combine 学习(三):Subscription和 SubscriberSwift Combine 学习(四&…...

Vue-router知识点汇总
import Vue from vue import Router from vue-router Vue.use(Router) import Layout from /layout export const constantRoutes [{path: /forgetpsd,name: forgetPsd,// 命名路由 ,跳转<router-link :to"{ name: forgetPsdr, params: { userId: 123 }}&q…...
java AQS
什么是AQS AQS(AbstractQueuedSynchronizer,抽象队列同步器)是 Java 中并发控制的一种机制,位于 java.util.concurrent.locks 包下,它为构建锁、信号量等同步工具提供了一个框架。AQS 通过 队列 来管理多个线程之间的…...
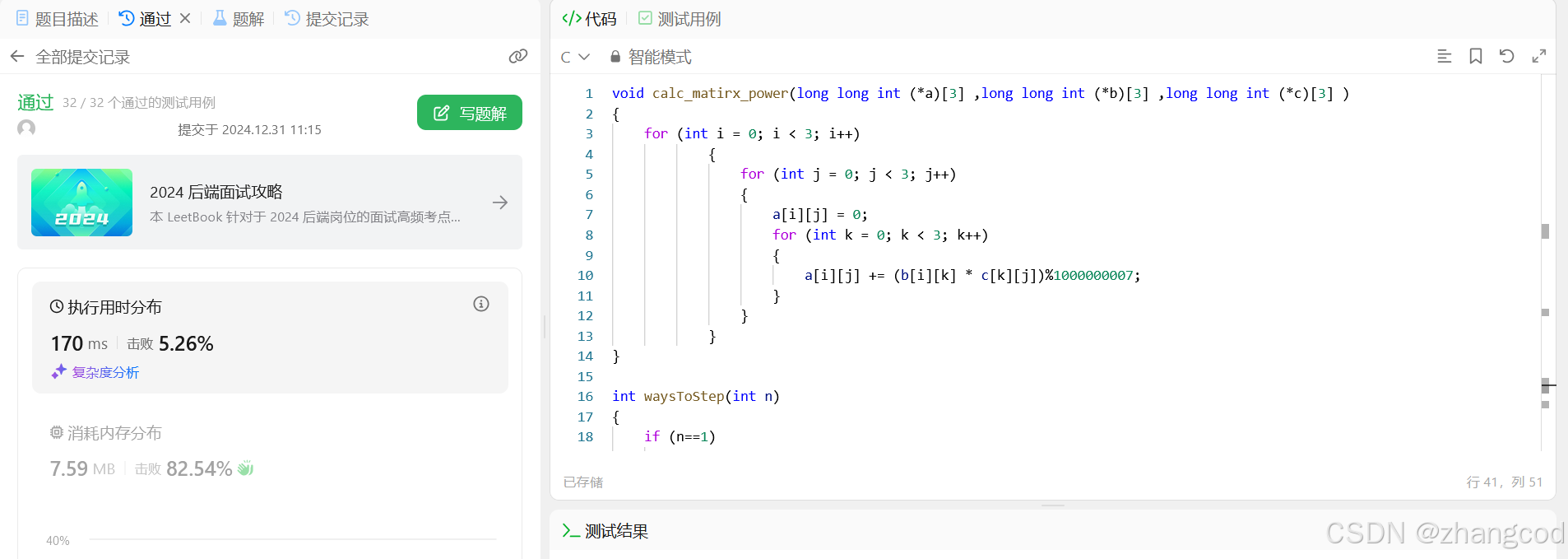
L25.【LeetCode笔记】 三步问题的四种解法(含矩阵精彩解法!)
目录 1.题目 2.三种常规解法 方法1:递归做 编辑 方法2:改用循环做 初写的代码 提交结果 分析 修改后的代码 提交结果 for循环的其他写法 提交结果 方法3:循环数组 提交结果 3.方法4:矩阵 算法 代码实践 1.先计算矩阵n次方 2.后将矩阵n次方嵌入递推式中 提…...

sdut-C语言实验-合数分解
sdut-C语言实验-合数分解 分数 12 全屏浏览 切换布局 作者 马新娟 单位 山东理工大学 合数是指在大于1的整数中,除了1和本身外,还能被其他数整除的数。例如,4、6、8、9、10等都是合数。把一个合数分解成若干个质因数乘积的形式(即求质因…...

深入理解 pytest Fixture 方法及其应用
在 Python 自动化测试领域,pytest 是当之无愧的王者。提到 pytest,不得不说它的一大核心功能——Fixture。Fixture 的强大,让复杂的测试流程变得井井有条,让测试代码更加灵活和可复用。 那么,pytest 的 Fixture 究竟是…...

在Linux上获取MS(如Media Server)中的RTP流并录制为双轨PCM格式的WAV文件
在Linux上获取MS(如Media Server)中的RTP流并录制为双轨PCM格式的WAV文件 一、RTP流与WAV文件格式二、实现步骤三、伪代码示例四、C语言示例代码五、关键点说明六、总结在Linux操作系统上,从媒体服务器(如Media Server,简称MS)获取RTP(Real-time Transport Protocol)流…...
Midjourney技术浅析(八):交互与反馈
Midjourney 的用户交互与反馈通过用户输入(User Input)和用户反馈(User Feedback)机制,不断优化和改进图像生成的质量和用户满意度。 一、用户交互与反馈模块概述 用户交互与反馈模块的主要功能包括: 1.…...
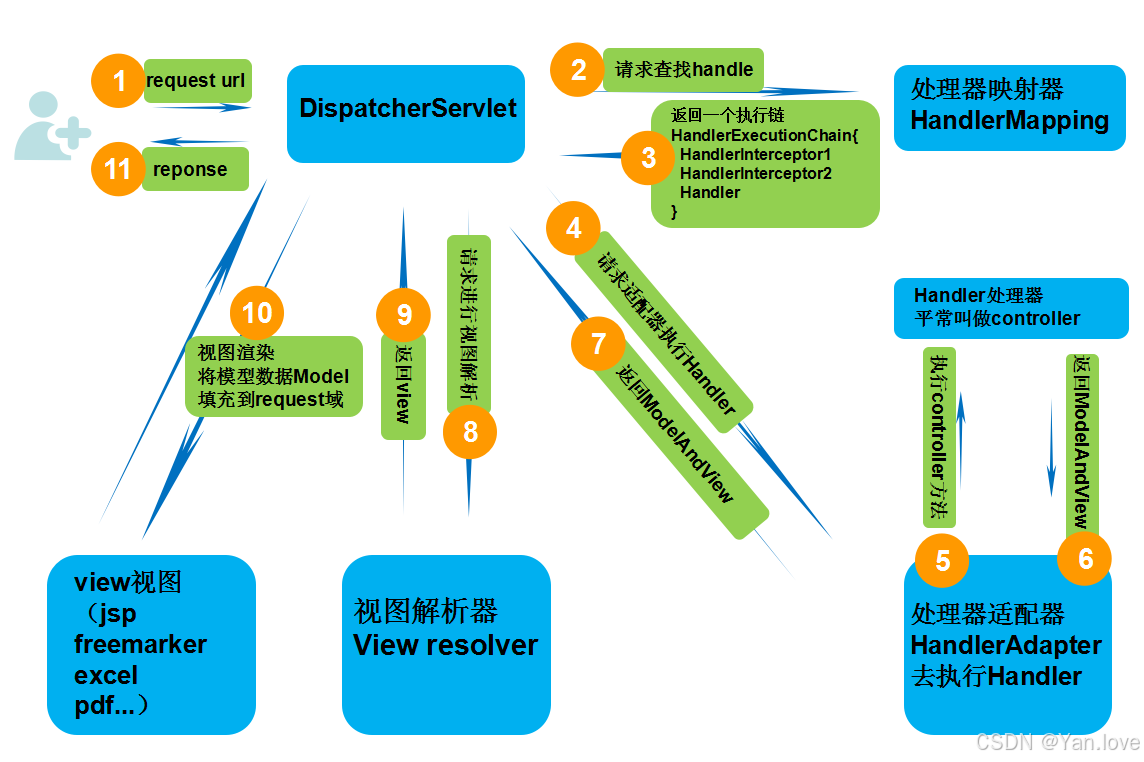
【Spring MVC 核心机制】核心组件和工作流程解析
在 Web 应用开发中,处理用户请求的逻辑常常会涉及到路径匹配、请求分发、视图渲染等多个环节。Spring MVC 作为一款强大的 Web 框架,将这些复杂的操作高度抽象化,通过组件协作简化了开发者的工作。 无论是处理表单请求、生成动态页面&#x…...
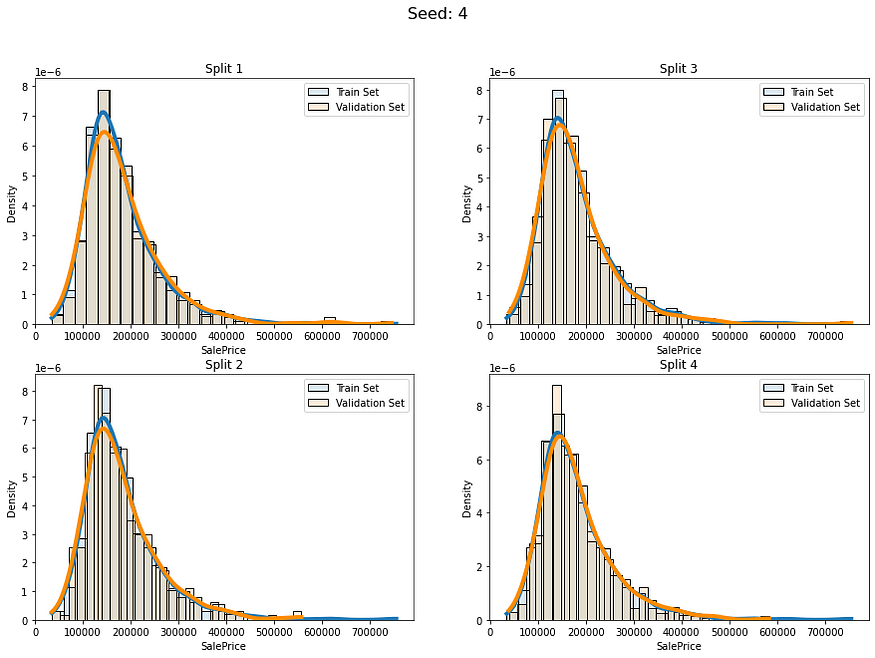
回归问题的等量分层
目录 一、说明 二、什么是分层抽样? 三、那么回归又如何呢? 四、回归分层(Stratification on Regression) 一、说明 在同一个数据集中,我们可以看成是一个抽样体。然而,我们如果将这个抽样体分成两份&#…...
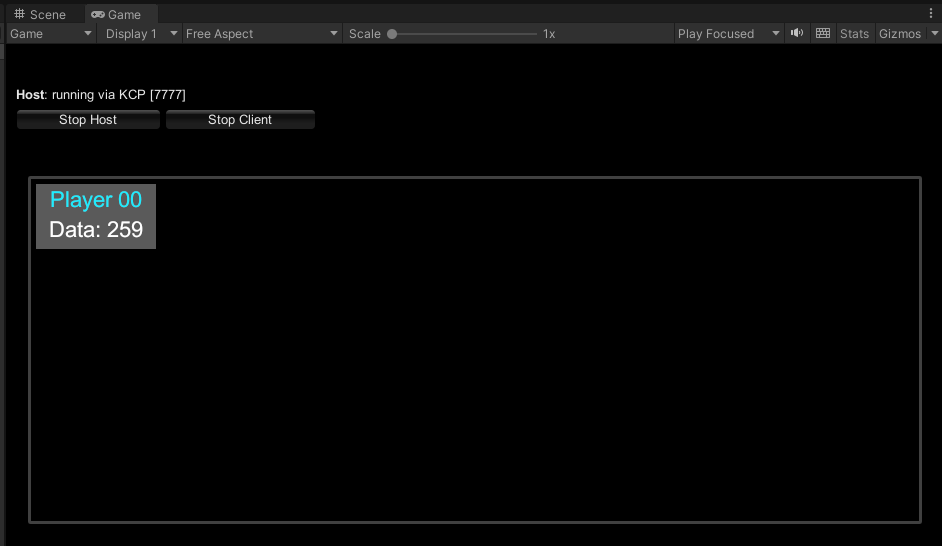
Unity-Mirror网络框架-从入门到精通之Basic示例
文章目录 前言Basic示例场景元素预制体元素代码逻辑BasicNetManagerPlayer逻辑SyncVars属性Server逻辑Client逻辑 PlayerUI逻辑 最后 前言 在现代游戏开发中,网络功能日益成为提升游戏体验的关键组成部分。Mirror是一个用于Unity的开源网络框架,专为多人…...

CSS 图片廊:网页设计的艺术与技巧
CSS 图片廊:网页设计的艺术与技巧 引言 在网页设计中,图片廊是一个重要的组成部分,它能够以视觉吸引的方式展示图片集合,增强用户的浏览体验。CSS(层叠样式表)作为网页设计的主要语言之一,提供…...

AI 发展的第一驱动力:人才引领变革
在科技蓬勃发展的当下,AI 成为了时代的焦点,然而其发展并非一帆风顺,究竟什么才是推动 AI 持续前行的关键力量呢? 目录 AI 发展现状剖析 期望与现实的落差 落地困境根源 人才:AI 发展的核心动力编辑 技术突破的…...
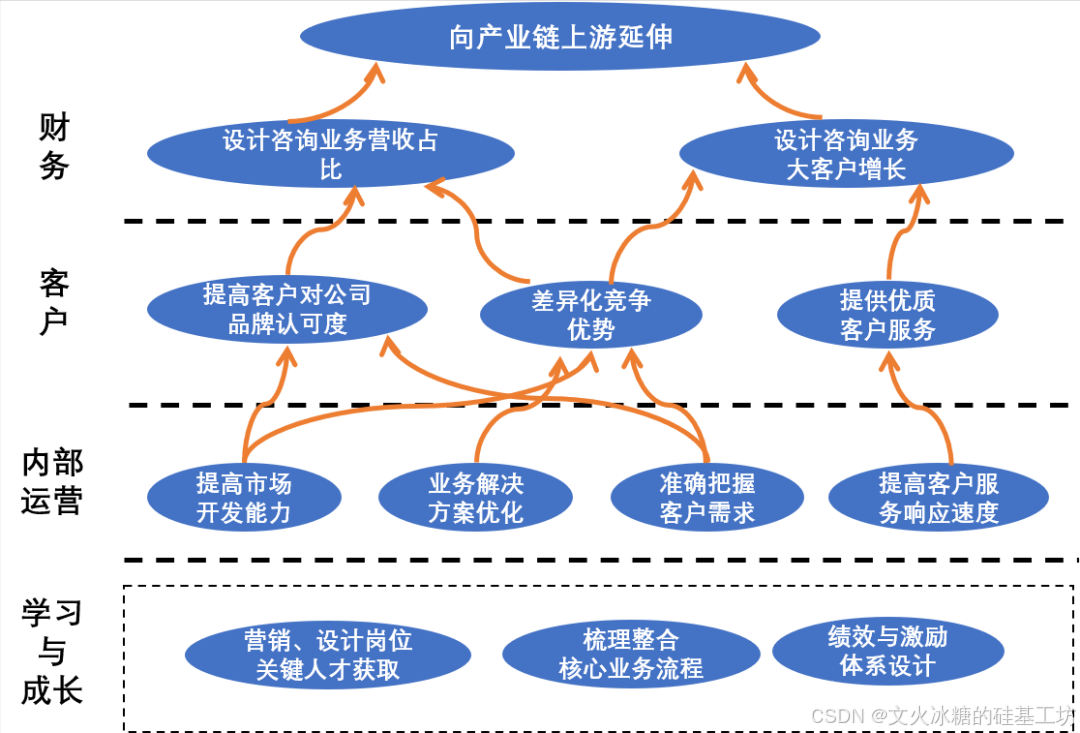
[创业之路-229]:《华为闭环战略管理》-5-平衡记分卡与战略地图
目录 一、平衡记分卡 1. 财务角度: 2. 客户角度: 3. 内部运营角度: 4. 学习与成长角度: 二、BSC战略地图 1、核心内容 2、绘制目的 3、绘制方法 4、注意事项 一、平衡记分卡 平衡记分卡(Balanced Scorecard&…...
用uniapp写一个播放视频首页页面代码
效果如下图所示 首页有导航栏,搜索框,和视频列表, 导航栏如下图 搜索框如下图 视频列表如下图 文件目录 视频首页页面代码如下 <template> <view class"video-home"> <!-- 搜索栏 --> <view class…...

【视觉SLAM:八、后端Ⅰ】
视觉SLAM的后端主要解决状态估计问题,它是优化相机轨迹和地图点的过程,从数学上看属于非线性优化问题。后端的目标是结合传感器数据,通过最优估计获取系统的状态(包括相机位姿和场景结构),在状态估计过程中…...

PaddleOCROCR关键信息抽取训练过程
步骤1:python版本3.8.20 步骤2:下载代码,安装依赖 git clone https://gitee.com/PaddlePaddle/PaddleOCR.git pip uninstall opencv-python -y # 安装PaddleOCR的依赖 ! pip install -r requirements.txt # 安装关键信息抽取任务的依赖 !…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...
