期末算法分析程序填空题
目录
5-1 最小生成树(普里姆算法)
5-2 快速排序(分治法)
输入样例:
输出样例:
5-3 归并排序(递归法)
输入样例:
输出样例:
5-4 求解编辑距离问题(动态规划法)
输入格式:
输出格式:
输入样例1:
输出样例1:
5-5 求解会议安排问题(动态规划)
输入格式:
输出格式:
输入样例1:
输出样例1:
5-6 求解n皇后问题(递归回溯法)
输入格式:
输出格式:
输入样例1:
输出样例1:
5-7 0/1背包问题(回溯法)
输入格式:
输出格式:
输入样例1:
输出样例1:
5-8 0/1背包问题(分支限界法)
输入格式:
输出格式:
输入样例1:
输出样例1:
输入样例2:
输出样例2:
5-9 部分背包问题(贪心法)
输入格式:
输出格式:
输入样例1:
输出样例1:
5-10 两个字符串的最长公共子序列长度
5-1 最小生成树(普里姆算法)
最小生成树(普里姆算法)。
#include <iostream> #define MVNum 100 #define MaxInt 32767 using namespace std;struct edge{char adjvex;int lowcost; }closedge[MVNum];typedef struct{ char vexs[MVNum]; int arcs[MVNum][MVNum]; int vexnum,arcnum; }AMGraph;int LocateVex(AMGraph G , char v);//实现细节隐藏 int CreateUDN(AMGraph &G);//实现细节隐藏int Min(AMGraph G){int i;int index = -1;int min = MaxInt;for(i = 0 ; i < G.vexnum ; ++i){if(){min = closedge[i].lowcost;index = i;}}return index; }void MiniSpanTree_Prim(AMGraph G, char u){ int k , j , i;char u0 , v0;k =LocateVex(G, u);for(j = 0; j < G.vexnum; ++j){ if(j != k){ closedge[j].adjvex = ;closedge[j].lowcost = ;}}closedge[k].lowcost = ;for(i = 1; i < G.vexnum; ++i){k = ; u0 = closedge[k].adjvex;v0 = G.vexs[k]; cout << u0 << "->" << v0 << endl;closedge[k].lowcost = ; for(j = 0; j < G.vexnum; ++j) if(G.arcs[k][j] < closedge[j].lowcost){closedge[j].adjvex = ;closedge[j].lowcost = ;}} }int main(){AMGraph G;CreateUDN(G);char u;cin >> u;MiniSpanTree_Prim(G , u);return 0; }
第一空:min > closedge[i].lowcost && closedge[i].lowcost != 0
第二空:u
第三空:G.arcs[k][j]
第四空:0
第五空:Min(G)
第六空:0
第七空:G.vexs[k]
第八空:G.arcs[k][j]
5-2 快速排序(分治法)
快速排序。
#include <iostream> #define MAXSIZE 1000 using namespace std;typedef struct {int key;char *otherinfo; }ElemType;typedef struct {ElemType *r;int length; }SqList;int Partition(SqList &L,int low,int high) { int pivotkey;L.r[0]=L.r[low]; pivotkey=L.r[low].key;while(){while() --high;L.r[low]=L.r[high]; while() ++low;L.r[high]=L.r[low];}L.r[low]=L.r[0];return low; }void QSort(SqList &L,int low,int high) {int pivotloc;if(low<high){ pivotloc=;;;} }void QuickSort(SqList &L) {QSort(L,1,L.length); }void Create_Sq(SqList &L) {int i,n;cin>>n; //输入的值不大于 MAXSIZEfor(i=1;i<=n;i++){cin>>L.r[i].key;L.length++;} } void show(SqList L) {int i;for(i=1;i<=L.length;i++)if(i==1) cout<<L.r[i].key;elsecout<<" "<<L.r[i].key; }int main() {SqList L;L.r=new ElemType[MAXSIZE+1];L.length=0;Create_Sq(L);QuickSort(L);show(L);return 0; }输入样例:
第一行输入一个数n(输入的值不大于 MAXSIZE),接下来输入n个数。
7 24 53 45 45 12 24 90输出样例:
输出按升序排序的结果。
12 24 24 45 45 53 90
第一空:low < high
第二空:low < high && L.r[high].key >= pivotkey
第三空:low < high && L.r[low].key <= pivotkey
第四空:Partition(L,low,high)
第五空:QSort(L,low,pivotloc-1)
第六空:QSort(L,pivotloc+1,high)
5-3 归并排序(递归法)
归并排序(递归法)。
#include <iostream> #define MAXSIZE 1000 using namespace std;typedef struct {int key;char *otherinfo; }ElemType;typedef struct {ElemType *r;int length; }SqList;void Create_Sq(SqList &L) {int i,n;cin>>n; //输入的值不大于 MAXSIZEfor(i=1;i<=n;i++){cin>>L.r[i].key;L.length++;} } void show(SqList L) {int i;for(i=1;i<=L.length;i++)if(i==1) cout<<L.r[i].key;elsecout<<" "<<L.r[i].key; }void Merge(ElemType R[],ElemType T[],int low,int mid,int high) { int i,j,k;i=low; j=mid+1;k=low; while(i<=mid&&j<=high){ if(R[i].key<=R[j].key) T[k++]=R[i++]; else T[k++]=R[j++]; } while(i<=mid)T[k++]=R[i++]; while(j<=high)T[k++]=R[j++]; } void MSort(ElemType R[],ElemType T[],int low,int high) { int mid;ElemType *S=new ElemType[MAXSIZE];if(low==high) ; else{ mid=(low+high)/2;;; ;} } void MergeSort(SqList &L) { MSort(L.r,L.r,1,L.length); } int main() {SqList R;R.r=new ElemType[MAXSIZE+1];R.length=0;Create_Sq(R);MergeSort(R);show(R);return 0; }输入样例:
第一行输入一个数n,接下来输入n个数。
7 24 53 45 45 12 24 90输出样例:
输出排序结果。
12 24 24 45 45 53 90
第一空:T[low]=R[low]
第二空:MSort(R,S,low,mid)
第三空:MSort(R,S,mid+1,high)
第四空:Merge(S,T,low,mid,high)
5-4 求解编辑距离问题(动态规划法)
设A和B是两个字符串。现在要用最少的字符操作次数,将字符串A转换为字符串B。这里所说的字符操作共有3种:
(1)删除一个字符。
(2)插入一个字符。
(3)将一个字符替换另一个字符。#include<stdio.h> #include<string> #include<iostream> #include<algorithm> using namespace std; #define MAX 201 //问题表示 string a; string b; //求解结果表示 int dp[MAX][MAX]; void solve() //求dp {int i,j;for (i=1;i<=a.length();i++) dp[i][0]=i; //把a的i个字符全部删除转换为bfor (j=1; j<=b.length(); j++)dp[0][j]=j; //在a中插入b的全部字符转换为bfor (i=1; i<=a.length(); i++)for (j=1; j<=b.length(); j++){if (a[i-1]==b[j-1]);elsedp[i][j]=;} } int main() { cin>>a>>b;solve();printf("%d",dp[a.length()][b.length()]);return 0; }输入格式:
第一行输入A字符串,第二行输入B字符串。
输出格式:
输出最少的字符操作次数。
输入样例1:
sfdqxbw gfdgw输出样例1:
4
第一空:dp[i][j]=dp[i-1][j-1]
第二空: min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1
5-5 求解会议安排问题(动态规划)
陈老师是一个比赛队的主教练。有一天,他想与团队成员开会,应该为这次会议安排教室。教室非常缺乏,所以教室管理员必须接受订单和拒绝订单以优化教室的利用率。如果接受一个订单,该订单的开始时间和结束时间成为一个活动。每个时间段只能安排一个订单(即假设只有一个教室)。请你找出一个最大化的总活动时间的方法。你的任务是这样的:读入订单,计算所有活动(接受的订单)占用时间的最大值。
#include <stdio.h> #include <string.h> #include <vector> #include <algorithm> #include <iostream> using namespace std; #define MAX 101 //问题表示 struct NodeType {int b; //开始时间int e; //结束时间int length; //订单的执行时间 };bool cmp(const NodeType &a,const NodeType &b) { //用于排序的运算符重载函数return a.e<b.e; //按结束时间递增排序 }int n; //订单个数 NodeType A[MAX]; //存放订单 //求解结果表示 int dp[MAX]; //动态规划数组 int pre[MAX]; //pre[i]存放前驱订单编号 void solve();int main() {cin>>n;for(int i=0;i<n;i++)cin>>A[i].b>>A[i].e;for (int i=0; i<n; i++)A[i].length=A[i].e-A[i].b;solve();cout<<dp[n-1]; return 0; }void solve() //求dp和pre {memset(dp,0,sizeof(dp)); //dp数组初始化stable_sort(A,A+n,cmp); //采用稳定的排序算法dp[0]=A[0].length;pre[0]=-1;for (int i=1;i<n;i++){int low=0, high=i-1;while(low<=high) //在A[0..i-1]中查找结束时间早于A[i]开始时间的最晚订单A[low-1]{int mid=(low+high)/2;if(A[mid].e<=A[i].b)low=mid+1;elsehigh=mid-1;}if (low==0) //特殊情况{if(dp[i-1]>=A[i].length){dp[i]=;pre[i]=-2; //不选中订单i}else{dp[i]=;pre[i]=-1; //没有前驱订单}}else //A[i]前面最晚有兼容订单A[low-1]{if (dp[i-1]>=dp[low-1]+A[i].length){dp[i]=;pre[i]=-2; //不选中订单i}else{dp[i]=;pre[i]=low-1; //选中订单i}}} }输入格式:
第一行是一个整数n,接着的n行中每一行包括两个整数b和e,其中b是一个订单开始时间,e是的结束时间。。
输出格式:
输出一行包括所有活动占用时间的最大值。
输入样例1:
11 1 4 3 5 0 6 5 7 3 8 5 9 6 10 8 11 8 12 2 13 12 15输出样例1:
13
第一空:dp[i-1]
第二空:A[i].length
第三空:dp[i-1]
第四空:dp[low-1]+A[i].length
5-6 求解n皇后问题(递归回溯法)
在n×n的方格棋盘上,放置n个皇后,要求每个皇后不同行、不同列、不同左右对角线。如下图所示是6皇后问题的一个解。
#include <stdio.h> #include <stdlib.h> #define N 20 //最多皇后个数 int q[N]; //存放各皇后所在的列号,即(i,q[i])为一个皇后位置void dispasolution(int n) //输出n皇后问题的一个解 {for (int i=1;i<=n;i++)printf("(%d,%d)",i,q[i]);printf("\n"); }bool place(int i,int j) //测试(i,j)位置能否摆放皇后 {if (i==1) return true; //第一个皇后总是可以放置int k=1;while (k<i) //k=1~i-1是已放置了皇后的行{ if ((q[k]==j) || (abs(q[k]-j)==abs(i-k)));k++;}; }void queen(int i,int n) //放置1~i的皇后 { if (i>n) dispasolution(n); //所有皇后放置结束else{for (int j=1;j<=n;j++) //在第i行上试探每一个列jif () //在第i行上找到一个合适位置(i,j){ q[i]=j;;}} }int main() { int n; //n为存放实际皇后个数scanf("%d",&n);if (n<=20)queen(1,n); //放置1~i的皇后return 0; }输入格式:
输入n。
输出格式:
按行输出每组解。
输入样例1:
6输出样例1:
(1,2)(2,4)(3,6)(4,1)(5,3)(6,5) (1,3)(2,6)(3,2)(4,5)(5,1)(6,4) (1,4)(2,1)(3,5)(4,2)(5,6)(6,3) (1,5)(2,3)(3,1)(4,6)(5,4)(6,2)
第一空:return false
第二空:return true
第三空:place(i,j)
第四空:queen(i+1,n)
5-7 0/1背包问题(回溯法)
0/1背包问题。给定一载重量为W的背包及n个重量为wi、价值为vi的物体,1≤i≤n,要求而且重量和恰好为W具有最大的价值。
#include <stdio.h> #include <string.h> #include <iostream> #define MAXN 20 //最多物品数 using namespace std; int n; //物品数 int W; //限制重量 int w[MAXN]={0}; //存放物品重量,不用下标0元素 int v[MAXN]={0}; //存放物品价值,不用下标0元素 int x[MAXN]; //存放最终解 int maxv; //存放最优解的总价值 void dfs(int i,int tw,int tv,int rw,int op[]) //求解0/1背包问题 {int j;if (i>n) //找到一个叶子结点{ if () //找到一个满足条件的更优解,保存它{ maxv=tv;for () //复制最优解x[j]=op[j];}}else //尚未找完所有物品{ if () //左孩子结点剪枝:满足条件时才放入第i个物品{op[i]=1; //选取第i个物品dfs();}op[i]=0; //不选取第i个物品,回溯if () //右孩子结点剪枝dfs();} } void dispasolution() //输出最优解 { int i;for (i=1;i<=n;i++)if (x[i]==1)printf("%d ",i);printf("\n%d %d",W,maxv); } int main() {int i;cin>>n>>W; //输入物体个数及背包载重量 for(int i=1;i<=n;i++)//输入各物体重量及价值 cin>>w[i]>>v[i];int op[MAXN]; //存放临时解memset(op,0,sizeof(op));int rw=0;for (int i=1;i<=n;i++)rw+=w[i];dfs(1,0,0,rw,op);dispasolution();return 0; }输入格式:
第一行输入背包载重量W及背包个数n,再依次输入n行,每行为背包重量wi和价值vi。
输出格式:
第一行输出输出装入背包内的物体编号(末尾有空格),第二行输出背包内的物体总重量和总价值。
输入样例1:
5 10 2 6 2 3 6 5 5 4 4 6输出样例1:
1 2 3 10 14
第一空:tw==W && tv>maxv
第二空:j=1;j<=n;j++
第三空:tw+w[i]<=W
第四空:i+1,tw+w[i],tv+v[i],rw-w[i],op
第五空:tw+rw>W
第六空:i+1,tw,tv,rw-w[i],op
5-8 0/1背包问题(分支限界法)
0/1背包问题。给定一载重量为m的背包及n个重量为wi、价值为vi的物体,1≤i≤n,要求把物体装入背包,使背包的物体价值最大。
输入格式:
第一行输入背包载重量m及背包个数n,再依次输入n行,每行为背包重量wi和价值vi。
输出格式:
第一行输出输出所求X[n]数组,第二行输出装入背包内的物体的最大价值。
输入样例1:
5 10 2 6 2 3 6 5 5 4 4 6输出样例1:
11001 15输入样例2:
5 10 11 2 13 10 12 5 13 3 11 6输出样例2:
00 0#include <stdio.h> #include <queue> #include <iostream> using namespace std; #define MAXN 20 //最多可能物品数 //问题表示 int n,W; int w[MAXN+1]; //重量,下标0不用 int v[MAXN+1]; //价值,下标0不用 //求解结果表示 int maxv=-9999; //存放最大价值,初始为最小值 int bestx[MAXN+1]; //存放最优解,全局变量 int total=1; //解空间中结点数累计,全局变量 struct NodeType //队列中的结点类型 { int no; //结点编号int i; //当前结点在搜索空间中的层次int w; //当前结点的总重量int v; //当前结点的总价值int x[MAXN+1]; //当前结点包含的解向量double ub; //上界 };void bound(NodeType &e) //计算分枝结点e的上界 {int i=e.i+1;int sumw=e.w;double sumv=e.v;while (){ sumw+=w[i]; //计算背包已装入载重sumv+=v[i]; //计算背包已装入价值i++;}if (i<=n) e.ub=;elsee.ub=sumv; }void EnQueue(NodeType e,queue<NodeType> &qu) //结点e进队qu {if (e.i==n) //到达叶子结点{if (e.v>maxv) //找到更大价值的解{;for (int j=1;j<=n;j++);}}else qu.push(e); //非叶子结点进队 } void bfs() //求0/1背包的最优解 {int j;NodeType e,e1,e2; //定义3个结点queue<NodeType> qu; //定义一个队列e.i=0; //根结点置初值,其层次计为0e.w=0; e.v=0;e.no=total++; for (j=1;j<=n;j++)e.x[j]=0;bound(e); //求根结点的上界qu.push(e); //根结点进队while (!qu.empty()) //队不空循环{e=qu.front(); qu.pop(); //出队结点ee1.no=total++; e1.i=e.i+1; //建立左孩子结点e1.w=e.w+w[e1.i];e1.v=e.v+v[e1.i];for (j=1;j<=n;j++) //复制解向量e1.x[j]=e.x[j];e1.x[e1.i]=1;bound(e1); //求左孩子结点的上界 if () //剪枝:检查左孩子结点{EnQueue(e1,qu); //左孩子结点进队操作}e2.no=total++; //建立右孩子结点e2.i=e.i+1;e2.w=; e2.v=;for (j=1;j<=n;j++) //复制解向量e2.x[j]=e.x[j];e2.x[e2.i]=;bound(e2); //求右孩子结点的上界if () //若右孩子结点可行,则进队,否则被剪枝EnQueue(e2,qu);} } int main() {cin>>n>>W; //输入物体个数及背包载重量 for(int i=1;i<=n;i++)//输入各物体重量及价值 cin>>w[i]>>v[i]; bfs(); //调用队列式分枝限界法求0/1背包问题for(int i=1;i<=n;i++)printf("%d",bestx[i]);printf("\n%d",maxv);return 0; }
第一空:(sumw+w[i]<=W) && i<=n
第二空:sumv+(W-sumw)*v[i]/w[i]
第三空:maxv=e.v
第四空:bestx[j]=e.x[j]
第五空:e.w+w[e.i+1]<=W&&e1.ub>maxv
第六空:e.w
第七空:e.v
第八空:0
第九空:e2.ub>maxv
5-9 部分背包问题(贪心法)
设有编号为1、2、…、n的n个物品,它们的重量分别为w1、w2、…、wn,价值分别为v1、v2、…、vn,其中wi、vi(1≤i≤n)均为正数。
有一个背包可以携带的最大重量不超过W。求解目标:在不超过背包负重的前提下,使背包装入的总价值最大。#include <stdio.h> #include <string.h> #include <iostream> #include <algorithm> using namespace std; #define MAXN 51 //问题表示 int n; double W; //限重 struct NodeType { int no;double w;double v;double p; //p=v/wfloat x;bool operator<(const NodeType &s) const{return p>s.p; //按p递减排序} }; NodeType A[MAXN]={{0}}; //下标0不用 //求解结果表示 double V; //最大价值 bool cmp(const NodeType &a,const NodeType &b) {return a.no<b.no; }void Knap() //求解背包问题并返回总价值 {V=0; //V初始化为0double weight=W; //背包中能装入的余下重量int i=1;while () { A[i].x=1; //装入物品i; V+=A[i].v; //累计总价值; }if (weight>0) //当余下重量大于0{ A[i].x=;V+=A[i].x*A[i].v; //累计总价值} }int main() { cin>>n>>W;for(int i=1;i<=n;i++){cin>>A[i].no>>A[i].w>>A[i].v;A[i].x=0;}for (int i=1;i<=n;i++) //求v/wA[i].p=A[i].v/A[i].w;sort(A+1,A+n+1); //排序Knap();sort(A+1,A+n+1,cmp);for(int j=1;j<=n;j++)cout<<A[j].no<<" "<<A[j].x*A[j].v<<endl;cout<<V;return 0; }输入格式:
第一行物品数n和背包容量W,接着的n行中输入每个物品的编号,重量和价值。
输出格式:
输出装入背包的物品信息,共n行,按物品编号递增排序的物品编号及重量(物品编号从1开始)。最后一行输出总价值。
输入样例1:
5 100 1 10 20 2 20 30 3 30 66 4 40 40 5 50 60输出样例1:
1 20 2 30 3 66 4 0 5 48 164
第一空:A[i].w<=weight
第二空:weight-=A[i].w
第三空:i++
第四空:weight/A[i].w
5-10 两个字符串的最长公共子序列长度
下面程序完成最长公共子序列的长度计算。
#include<stdio.h> #include<string.h> #define N 80 int C[N][N]; // 记录最长公共子序列 int rec[N][N]; // 记录轨迹 int LCSLength(char *X, char *Y) { int i,j,m=strlen(X),n=strlen(Y);for(i = 1; i <=m ; i++) {for(j = 1; j <= n; j++) {if() {C[i][j] = C[i-1][j-1] + 1;rec[i][j] = 1; //LU}else if() {C[i][j] = C[i-1][j]; rec[i][j] = 2; //U}else {C[i][j] = ;rec[i][j] = 3; //L}}}return C[m][n]; }
第一空:X[i]==Y[j]
第二空:C[i-1][j]>=C[i][j-1]
第三空:C[i][j-1]
相关文章:

期末算法分析程序填空题
目录 5-1 最小生成树(普里姆算法) 5-2 快速排序(分治法) 输入样例: 输出样例: 5-3 归并排序(递归法) 输入样例: 输出样例: 5-4 求解编辑距离问题(动态规划法)…...

搭建android开发环境 android studio
1、环境介绍 在进行安卓开发时,需要掌握java,需要安卓SDK,需要一款编辑器,还需要软件的测试环境(真机或虚拟机)。 早起开发安卓app,使用的是eclipse加安卓SDK,需要自行搭建。 目前开…...

R语言6种将字符转成数字的方法,写在新年来临之际
咱们临床研究中,拿到数据后首先要对数据进行清洗,把数据变成咱们想要的格式,才能进行下一步分析,其中数据中的字符转成数字是个重要的内容,因为字符中常含有特殊符号,不利于分析,转成数字后才能…...

RocketMQ学习笔记(持续更新中......)
目录 1. 单机搭建 2. 测试RocketMQ 3. 集群搭建 4. 集群启动 5. RocketMQ-DashBoard搭建 6. 不同类型消息发送 1.同步消息 2. 异步消息发送 3. 单向发送消息 7. 消费消息 1. 单机搭建 1. 先从rocketmq官网下载二进制包,ftp上传至linux服务器,…...
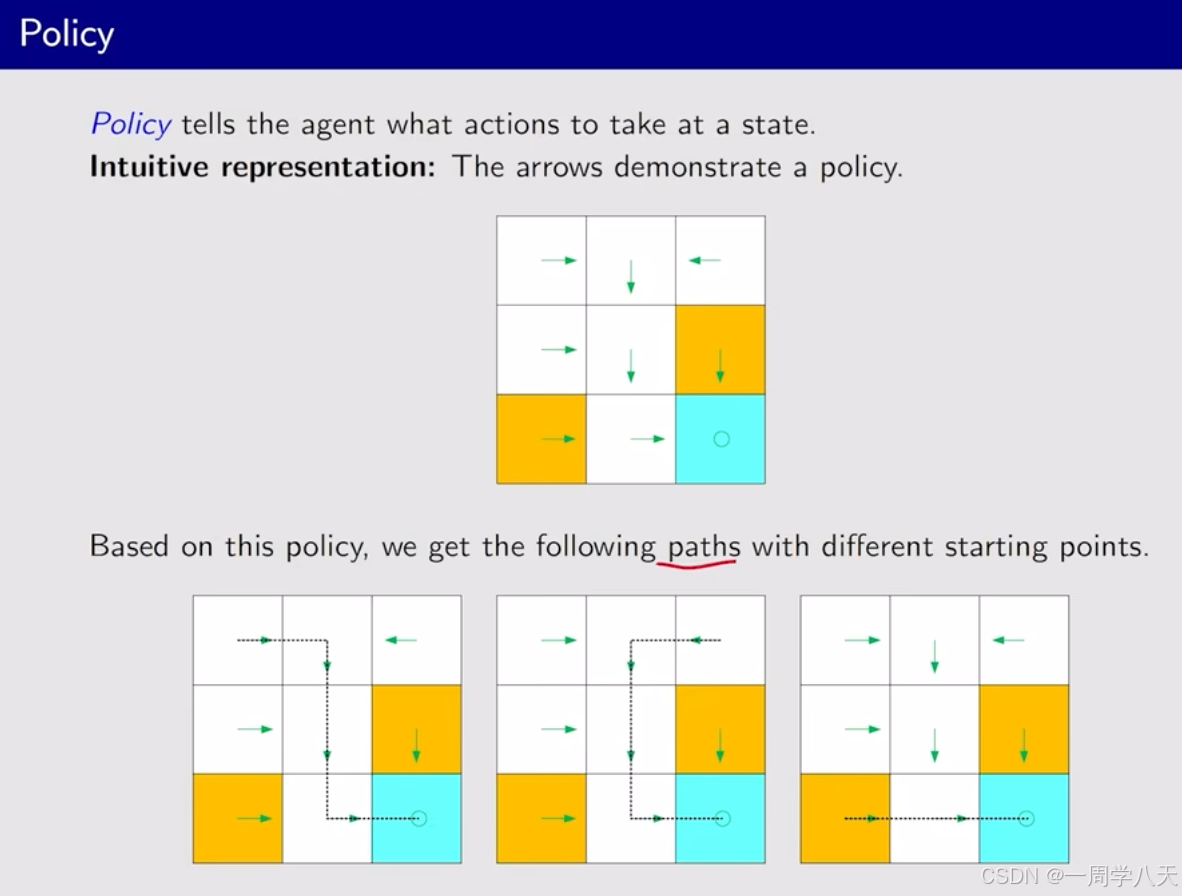
强化学习的基础概念
这节课会介绍一些基本的概念,并结合例子讲解。 在马尔科夫决策框架下介绍这些概念 本博客是基于西湖大学强化学习课程的视屏进行笔记的,这是链接: 课程链接 目录 强化学习的基本概念 state和state space Action和Action Space State transiti…...
)
excel怎么删除右边无限列(亲测有效)
excel怎么删除右边无限列(亲测有效) 网上很多只用第1步的,删除了根本没用,还是存在,但是隐藏后取消隐藏却是可以的。 找到右边要删除的列的第一个空白列,选中整个列按“ctrlshift>(向右的小箭头)”&am…...

STM32-笔记23-超声波传感器HC-SR04
一、简介 HC-SR04 工作参数: • 探测距离:2~600cm • 探测精度:0.1cm1% • 感应角度:<15 • 输出方式:GPIO • 工作电压:DC 3~5.5V • 工作电流:5.3mA • 工作温度:-40~85℃ 怎么…...

Linux | Ubuntu零基础安装学习cURL文件传输工具
目录 介绍 检查安装包 下载安装 手册 介绍 cURL是一个利用URL语法在命令行下工作的文件传输工具,首次发行于1997年12。cURL支持多种协议,包括FTP、FTPS、HTTP、HTTPS、TFTP、SFTP、Gopher、SCP、Telnet、DICT、FILE、LDAP、LDAPS、IMAP、POP3…...

什么是 GPT?Transformer 工作原理的动画展示
大家读完觉得有意义记得关注和点赞!!! 目录 1 图解 “Generative Pre-trained Transformer”(GPT) 1.1 Generative:生成式 1.1.1 可视化 1.1.2 生成式 vs. 判别式(译注) 1.2 Pr…...
)
SpringCloudAlibaba实战入门之路由网关Gateway过滤器(十三)
承接上篇,我们知道除了断言,还有一个重要的功能是过滤器,本节课我们就讲一下常见的网关过滤器及其一般使用。 一、Filter介绍 类似SpringMVC里面的的拦截器Interceptor,Servlet的过滤器。“pre”和“post”分别会在请求被执行前调用和被执行后调用,用来修改请求和响应信…...

电路仿真软件PSIM简介
在从事开关电源相关产品开发的工程师或者正在学习开关电源的学习者,常常会用到各种仿真软件进行电路的仿真,不仅可以快速验证电路参数,还能清楚知道各器件的工作状态。 现在的电路仿真软件很多,例如matlab、Multisim、Simplis&…...
C语言:调试的概念和调试器的选择
所谓调试(Dubug),就是跟踪程序的运行过程,从而发现程序的逻辑错误(思路错误),或者隐藏的缺陷(Bug)。 在调试的过程中,我们可以监控程序的每一个细节ÿ…...

25. C++继承 1 (继承的概念与基础使用, 继承的复制兼容规则,继承的作用域)
⭐上篇模板文章:24. C模板 2 (非类型模板参数,模板的特化与模板的分离编译)-CSDN博客 ⭐本篇代码:c学习 橘子真甜/c-learning-of-yzc - 码云 - 开源中国 (gitee.com) ⭐标⭐是比较重要的部分 目录 一. 继承的基础使用 1.1 继承的格式 1.2 …...

git 退出编辑模式
在使用 Git 时,有时需要进入编辑器来输入提交信息或进行其他编辑操作。不同的系统和配置可能会导致使用不同的编辑器。以下是几种常见 Git 编辑器的退出方法: Vim 编辑器: 保存并退出: 按下 Esc 键退出编辑模式。输入 :w…...

内容营销与传统营销方式有哪些差别?
在互联网高度发达的当下,碎片化的信息接收方式,让用户对于营销信息拥有较高的敏感度。这一现状,也使得众多传统营销方式正在逐渐失效。想要稳定推广效率,内容营销是当下不少品牌的共同选择。接下来,就让我们来了解下内…...

EasyExcel(读取操作和填充操作)
文章目录 1.准备Read.xlsx(具有两个sheet)2.读取第一个sheet中的数据1.模板2.方法3.结果 3.读取所有sheet中的数据1.模板2.方法3.结果 EasyExcel填充1.简单填充1.准备 Fill01.xlsx2.无模版3.方法4.结果 2.列表填充1.准备 Fill02.xlsx2.模板3.方法4.结果 …...
】)
【华为OD-E卷 - 机房布局 100分(python、java、c++、js、c)】
【华为OD-E卷 - 机房布局 100分(python、java、c、js、c)】 题目 小明正在规划一个大型数据中心机房,为了使得机柜上的机器都能正常满负荷工作,需要确保在每个机柜边上至少要有一个电箱。 为了简化题目,假设这个机房…...

【竞技宝】LOL:IG新赛季分组被质疑
北京时间2024年12月31日,今天已经2024年的最后一天,在进入一月之后,英雄联盟将迎来全新的2025赛季。而目前新赛季第一阶段的抽签结果已经全部出炉,其中人气最高的IG战队在本次抽签中抽到了“绝世好签”引来了网友们的质疑。 首先介…...

ChatBI来啦!NBAI 正式上线 NL2SQL 功能
NebulaAI 现已正式上线 NL2SQL 功能,免费开放使用! 什么是 NL2SQL?NL2SQL 即通过自然语言交互,用户可以轻松查询、分析和管理数据库中的数据(ChatBI),从此摆脱传统复杂的数据库操作。 欢迎免费…...
)
8. Web应用程序(Web)
8. Web应用程序(Web) Spring Boot 非常适用于Web应用程序开发。你可以使用嵌入式 Tomcat、Jetty、Undertow或Netty创建一个独立的HTTP服务器。大多是Web应用程序都会使用 spring-boot-starter-web 依赖模块来快速启动和运行项目。你也可以选择使用 spri…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...
