Levenshtein 距离的原理与应用
引言
在文本处理和自然语言处理(NLP)中,衡量两个字符串相似度是一项重要任务。Levenshtein 距离(也称编辑距离)是一种常见的算法,用于计算将一个字符串转换为另一个字符串所需的最少编辑操作次数。这些操作包括插入、删除和替换。
本文将详细介绍 Levenshtein 距离的原理,并通过 Python 代码示例展示其实际应用。
什么是 Levenshtein 距离?
Levenshtein 距离定义为两个字符串之间的最小编辑操作次数,使得一个字符串可以变为另一个字符串。允许的三种操作为:
- 插入一个字符;
- 删除一个字符;
- 替换一个字符。
例如:
"kitten"和"sitting"的 Levenshtein 距离为 3,因为可以通过以下三步完成转换:- 替换
'k'为's'; - 替换
'e'为'i'; - 在末尾插入
'g'。
- 替换
Levenshtein 距离的计算原理
Levenshtein 距离使用动态规划(Dynamic Programming)实现,其核心思想是将问题分解为多个子问题,通过递归公式逐步计算解决。
假设字符串 AA 长度为 mm,字符串 BB 长度为 nn,则动态规划表 dp[i][j]dp[i][j] 表示将 A[0:i]A[0:i] 转换为 B[0:j]B[0:j] 的最小编辑距离。
Levenshtein 距离的 Python 实现
我们用一个简单的 Python 函数实现 Levenshtein 距离:
def levenshtein_distance(a, b):m, n = len(a), len(b)# 初始化动态规划表dp = [[0] * (n + 1) for _ in range(m + 1)]# 填充边界条件for i in range(m + 1):dp[i][0] = ifor j in range(n + 1):dp[0][j] = j# 计算动态规划表for i in range(1, m + 1):for j in range(1, n + 1):cost = 0 if a[i - 1] == b[j - 1] else 1dp[i][j] = min(dp[i - 1][j] + 1, # 删除dp[i][j - 1] + 1, # 插入dp[i - 1][j - 1] + cost # 替换)return dp[m][n]# 示例
a = "kitten"
b = "sitting"
distance = levenshtein_distance(a, b)
print(f"'{a}' 和 '{b}' 的 Levenshtein 距离为: {distance}")
运行结果:
'kitten' 和 'sitting' 的 Levenshtein 距离为: 3
Levenshtein 距离的应用场景
-
拼写纠错
- Levenshtein 距离可用于计算用户输入与正确单词之间的相似度,从而推荐正确的单词。
- 例如输入
"recieve",通过计算与候选词的距离,可以推荐"receive"。
-
模糊匹配
- 在数据库中模糊查找类似记录,比如搜索
"Jon"时匹配"John"。 - 使用 Python 的 TheFuzz 库可以轻松实现。
- 在数据库中模糊查找类似记录,比如搜索
-
文本去重
- 用于检测相似文本并去重,例如处理社交媒体内容或产品描述。
-
DNA 序列比对
- Levenshtein 距离在生物信息学中也有重要应用,用于比较 DNA 或 RNA 序列的相似性。
使用 Python 库快速计算 Levenshtein 距离
除了手动实现外,我们还可以使用开源库 Levenshtein 或 TheFuzz 快速计算。
安装:
pip install python-Levenshtein
示例代码:
import Levenshteina = "kitten"
b = "sitting"
distance = Levenshtein.distance(a, b)
print(f"'{a}' 和 '{b}' 的 Levenshtein 距离为: {distance}")
结果:
'kitten' 和 'sitting' 的 Levenshtein 距离为: 3
总结
Levenshtein 距离是一种高效且实用的字符串相似度度量方法。通过动态规划算法实现,它在拼写纠错、模糊匹配和文本去重等领域得到了广泛应用。无论是从学习算法原理,还是通过现有库快速应用,Levenshtein 距离都能为开发者带来极大帮助。
其它
多个字符串比较的例子 (比较字符串(i love you )和(love he))
我们利用动态规划的方式,逐步计算字符串 "i love you " 和 "love he " 的 Levenshtein 距离,以下是详细的过程。
1. 初始化动态规划表
假设:
- A="iloveyou"A = "i love you "(长度为 10,包括空格)
- B="lovehe"B = "love he "(长度为 8,包括空格)
动态规划表 dpdp 大小为 (10+1)×(8+1)=11×9(10+1) \times (8+1) = 11 \times 9。
初始状态如下:
- 第一行填充列索引(从空字符串到
B的编辑距离) - 第一列填充行索引(从空字符串到
A的编辑距离)
| l | o | v | e | h | e | |||
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| i | 1 | |||||||
| 2 | ||||||||
| l | 3 | |||||||
| o | 4 | |||||||
| v | 5 | |||||||
| e | 6 | |||||||
| 7 | ||||||||
| y | 8 | |||||||
| o | 9 | |||||||
| u | 10 |
2. 填充动态规划表
根据递归公式:
dp[i][j]=min{dp[i−1][j]+1,删除dp[i][j−1]+1,插入dp[i−1][j−1]+cost,替换dp[i][j] = \min \begin{cases} dp[i-1][j] + 1, & \text{删除} \\ dp[i][j-1] + 1, & \text{插入} \\ dp[i-1][j-1] + \text{cost}, & \text{替换} \end{cases}
其中:
- 如果 A[i−1]=B[j−1]A[i-1] = B[j-1],则 cost=0\text{cost} = 0,否则 cost=1\text{cost} = 1。
填充过程:
-
i=1,j=1i = 1, j = 1(比较
'i'和'l'):- 插入:dp[1][0]+1=2dp[1][0] + 1 = 2
- 删除:dp[0][1]+1=2dp[0][1] + 1 = 2
- 替换:dp[0][0]+1=1dp[0][0] + 1 = 1
所以 dp[1][1]=1dp[1][1] = 1。
-
i=1,j=2i = 1, j = 2(比较
'i'和'o'):- 插入:dp[1][1]+1=2dp[1][1] + 1 = 2
- 删除:dp[0][2]+1=3dp[0][2] + 1 = 3
- 替换:dp[0][1]+1=2dp[0][1] + 1 = 2
所以 dp[1][2]=2dp[1][2] = 2。
... 依此类推。
最终动态规划表填充完成后如下:
| l | o | v | e | h | e | |||
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| i | 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 2 | 2 | 3 | 4 | 4 | 5 | 6 | |
| l | 3 | 2 | 3 | 3 | 4 | 5 | 5 | 6 |
| o | 4 | 3 | 2 | 3 | 4 | 5 | 6 | 6 |
| v | 5 | 4 | 3 | 2 | 3 | 4 | 5 | 6 |
| e | 6 | 5 | 4 | 3 | 2 | 3 | 4 | 5 |
| 7 | 6 | 5 | 4 | 3 | 2 | 3 | 4 | |
| y | 8 | 7 | 6 | 5 | 4 | 3 | 3 | 4 |
| o | 9 | 8 | 7 | 6 | 5 | 4 | 4 | 4 |
| u | 10 | 9 | 8 | 7 | 6 | 5 | 5 | 5 |
3. 结果
表格右下角的值 dp[10][8]=5dp[10][8] = 5,表示将 "i love you " 转换为 "love he " 需要 5次编辑操作。
4. 操作过程
通过回溯动态规划表,我们可以得到具体的编辑操作:
- 删除
'i'(从'i love you '中删除第一个字符) - 替换
'y'为'h' - 替换
'o'为'e' - 删除
' '(去掉额外的空格) - 删除
'u'
最终,得到字符串 "love he "。
相关文章:

Levenshtein 距离的原理与应用
引言 在文本处理和自然语言处理(NLP)中,衡量两个字符串相似度是一项重要任务。Levenshtein 距离(也称编辑距离)是一种常见的算法,用于计算将一个字符串转换为另一个字符串所需的最少编辑操作次数。这些操作…...
)
解决json.decoder.JSONDecodeError: Expecting value: line 1 column 1 (char 0)
前言 作者在读取json文件的时候出现上述报错,起初以为是自己json文件有问题,但借助在线工具查看后发现没问题,就卡住了,在debug的过程中发现了json文件读取的一个小坑,在此分享一下 解决过程 原代码 with open(anno…...

hive中的四种排序类型
1、Order by 全局排序 ASC(ascend): 升序(默认) DESC(descend): 降序 注意 :只有一个 Reducer,即使我们在设置set reducer的数量为多个,但是在执行了order by语句之后,当前此次的运算还是只有…...

Spring-AI讲解
Spring-AI langchain(python) langchain4j 官网: https://spring.io/projects/spring-ai#learn 整合chatgpt 前置准备 open-ai-key: https://api.xty.app/register?affPuZD https://xiaoai.plus/ https://eylink.cn/ 或者淘宝搜: open ai key魔法…...

【brew安装失败】DNS 查询 raw.githubusercontent.com 返回的是 0.0.0.0
从你提供的 nslookup 输出看,DNS 查询 raw.githubusercontent.com 返回的是 0.0.0.0,这通常意味着无法解析该域名或该域名被某些 DNS 屏蔽了。这种情况通常有几个可能的原因: 可能的原因和解决方法 本地 DNS 问题: 有可能是你的本…...

HTML——29. 音频引入二
<!DOCTYPE html> <html><head><meta charset"UTF-8"><title>音频引入</title></head><body><!--audio:在网页中引入音频IE8以及之前版本不支持属性名和属性值一样,可以只写属性名src属性:指定音频文件…...

代码随想录训练营第三十四天| 62.不同路径 63. 不同路径 II
62.不同路径 题目链接:62. 不同路径 - 力扣(LeetCode) 讲解链接:代码随想录 动态规划五步走 1 定义dp数组是到dp[i][j]时有dp[i][j]条路径 dp[i][j] :表示从(0 ,0)出发…...

V90伺服PN版组态配置<一>
1、添加PLC之后,继续博图中网络视图中添加新设备,添加伺服驱动器组态设备 2、SINAMICS V90 PN V1.0 3、修改驱动器的IP地址。 【注意】 在项目中提前做好项目规划,如PLC设备从192.168.0.1开始,顺序递增------个位数都是CPU设备…...

又一年。。。。。。
2024,浑浑噩噩的一年。 除了100以内的加减法(数据,数据,还是数据。。。。。。),似乎没做些什么。 脸盲症越来越重的,怕是哪天连自己都不认得自己的了。 看到什么,听到什…...

xterm + vue3 + websocket 终端界面
xterm.js 下载插件 // xterm npm install --save xterm// xterm-addon-fit 使终端适应包含元素 npm install --save xterm-addon-fit// xterm-addon-attach 通过websocket附加到运行中的服务器进程 npm install --save xterm-addon-attach <template><div :…...

医疗数仓业务数据采集与同步
业务数据采集与同步 业务采集组件配置业务数据同步概述数据同步策略选择数据同步工具概述1.1.4 全量表数据同步DataX配置文件生成全量表数据同步脚本增量表数据同步 MySQL - Maxwell - Kafka - Flume - HDFSMaxwell配置增量表首日全量同步 业务采集组件配置 Maxwell将业务采集到…...

数字孪生智慧水利与水务所包含的应用场景有哪些?二者有何区别
水利和水务是两个密切相关但有所区别的概念,它们在水资源管理和保护方面各自承担着不同的职责和功能。 定义 智慧水务:智慧水务是指通过物联网、大数据、云计算、人工智能等新一代信息技术,对城市供水、排水、污水处理、水质监测等水务系统…...

Qt Creator项目构建配置说明
QT安装好之后,在安装目录的Tools\QtCreator\bin下找到qtcreator.exe文件并双击打开 点击文件-新建文件或项目 选择Qt Widgets Application 设置项目名称以及路径 make工具选择qmake(cmake还未尝试过) 设置主界面对应类的名称、父类&#…...

进程间通信的“五大武器”
😄作者简介: 小曾同学.com,一个致力于测试开发的博主⛽️,主要职责:测试开发、CI/CD 如果文章知识点有错误的地方,还请大家指正,让我们一起学习,一起进步。 😊 座右铭:不…...
备考实战之循环结构(for循环语句)(六))
全国青少年信息学奥林匹克竞赛(信奥赛)备考实战之循环结构(for循环语句)(六)
实战训练1—输出九九乘法表 问题描述: 在学校里学过九九乘法表,编程实现打印九九乘法表。 输入格式: 无输入 输出格式: 1*11 2*12 2*24 3*13 3*26 3*39 4*14 4*28 4*312 4*416 5*15 5*210 5*315 5*420 5*525 6*16 6*212 6*318 6*424 6*5…...

封装echarts成vue component
封装echarts成vue component EChartsLineComponent 文章目录 封装echarts成vue component EChartsLineComponent封装说明重写重点EChartsLineComponent的源码 使用说明调用EChartsLineComponent示例源码 封装说明 为了减少一些公共代码和方便使用echarts的line图形,…...

uniapp Stripe 支付
引入 Stripe npm install stripe/stripe-js import { loadStripe } from stripe/stripe-js; Stripe 提供两种不同类型组件 Payment Element 和 Card Element:如果你使用的是 Payment Element,它是一个更高级别的组件,能够自动处理多种支…...

Windows onnxruntime编译openvino
理论上来说,可以直接访问 ONNXRuntime Releases 下载 dll 文件,然后从官方文档中下载缺少的头文件以直接调用,但我没有尝试过。 1. 下载 OpenVINO 包 从官网下载 OpenVINO 的安装包并放置在 C:\Program Files (x86) 路径下,例如…...
vue3+TS+vite中Echarts的安装与使用
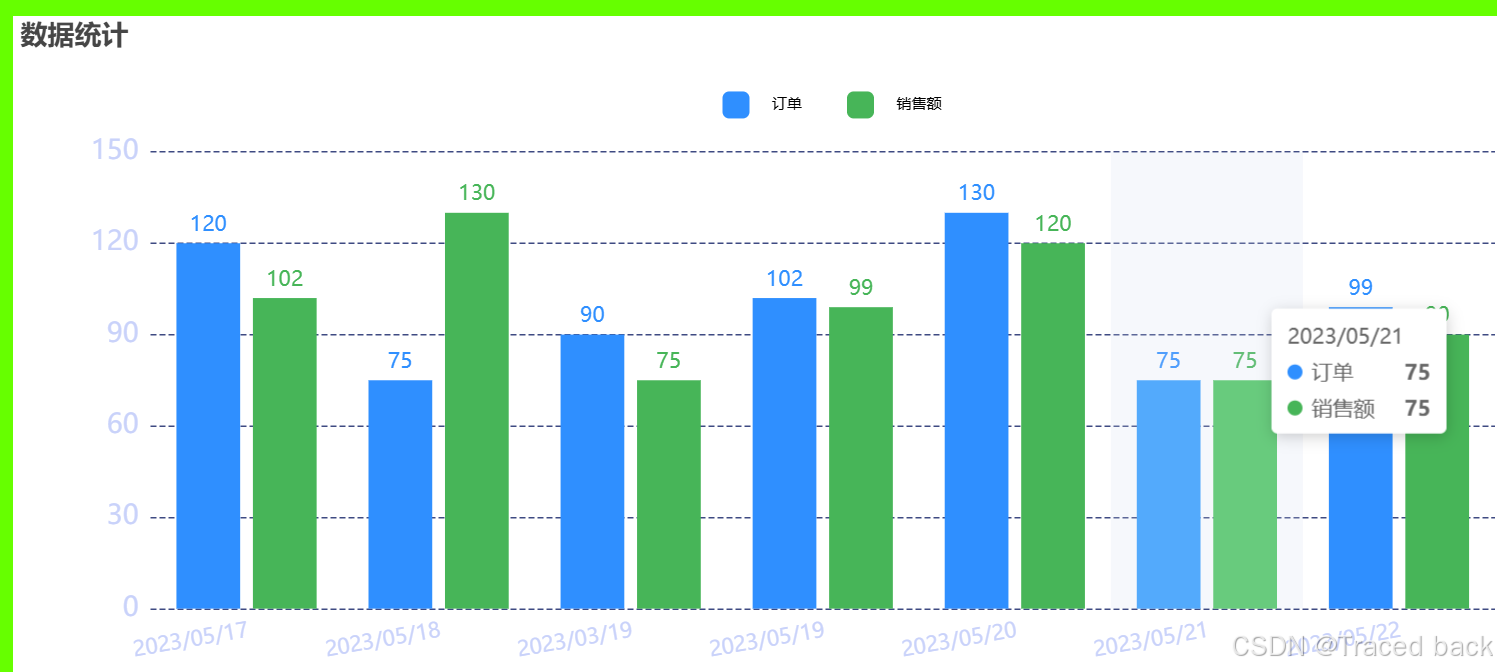
概述 技术栈:Vue3TsViteEcharts 简述:图文详解,教你如何在Vue项目中引入Echarts,封装Echarts组件,并实现常用Echats图列 文章目录 一,效果图 二,引入Echarts 2.1安装Echarts 2.2main.ts中引…...

期末算法分析程序填空题
目录 5-1 最小生成树(普里姆算法) 5-2 快速排序(分治法) 输入样例: 输出样例: 5-3 归并排序(递归法) 输入样例: 输出样例: 5-4 求解编辑距离问题(动态规划法)…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
