Docker新手:在tencent云上实现Python服务打包到容器
1 使用docker的原因
一致性和可移植性:Docker 容器可以在任何支持 Docker 的环境中运行,无论是开发者的笔记本电脑、测试服务器还是生产环境。这确保了应用在不同环境中的行为一致,减少了“在我的机器上可以运行”的问题。
隔离性:每个 Docker 容器都是独立的,拥有自己的文件系统、网络接口和进程空间。这使得不同应用之间不会互相干扰,提高了系统的稳定性和安全性。
资源效率:Docker 容器共享宿主机的操作系统内核,因此它们比虚拟机更轻量,启动速度更快,占用的资源更少。这使得在相同的硬件资源下可以运行更多的应用实例。
快速部署和扩展:Docker 容器可以快速启动和停止,这使得应用的部署和扩展变得非常容易。通过 Docker Compose 或 Kubernetes 等工具,可以轻松管理多个容器和服务。
2 docker与docker-compose的关系
Docker 用于管理单个容器,而 Docker Compose 用于管理多容器应用。
使用 Docker Compose 需要三个步骤:
- 用 Dockerfile 定义应用环境。
- 在
docker-compose.yml文件中定义应用服务。 - 运行
docker-compose up命令来启动和运行应用。
环境准备
ubuntu 22.04 LTS(腾讯云),python 3.10
文件目录结构是这样的
project/
├── app/
│ ├─ __init__.py
│ ├── app.py
│ └── requirements.txt
├── docker-compose.yml
└── Dockerfile
其中app.py的内容如下:
from app import app# 使用内存存储来替代 Redis
cache = {}def get_hit_count():# 检查 'hits' 键是否存在,如果不存在则初始化为 0if 'hits' not in cache:cache['hits'] = 0# 增加计数cache['hits'] += 1return cache['hits']@app.route('/')
def hello():count = get_hit_count()return f'Hello World! I have been seen {count} times.\n'# 只有直接运行此文件时才执行
if __name__ == '__main__':app.run(host='0.0.0.0', port=5000, debug=True)
init.py的代码如下:
from flask import Flaskapp = Flask(__name__)# 导入路由
from app.app import *
以下是创建一个基本的Python服务Dockerfile的步骤:
- 选择基础镜像:通常我们会选择官方提供的Python镜像作为基础。
- 设置工作目录:使用
WORKDIR指令设置容器内的工作目录。 - 复制文件:使用
COPY指令将本地文件复制到容器中。 - 安装依赖:使用
RUN pip install -r requirements.txt安装Python依赖。 - 暴露端口:使用
EXPOSE指令指定应用运行时需要暴露的端口。 - 定义启动命令:使用
CMD或ENTRYPOINT指令定义容器启动时执行的命令。
其中我的Dockerfile是这样的
# syntax=docker/dockerfile:1
FROM python:3.10-slim
WORKDIR /app
COPY app/requirements.txt .
RUN pip install --no-cache-dir -r requirements.txt
COPY . .
ENV FLASK_APP=app
ENV FLASK_ENV=development
EXPOSE 5000
CMD ["flask", "run", "--host=0.0.0.0"]
我的docker-compose.yml是这样的
version: '3.10'
services:web:build: .ports:- "5000:5000"volumes:- .:/appenvironment:- FLASK_APP=app.py- FLASK_ENV=development 如果Dockerfile和docker-compose不会写,可以找官网上的例子进行仿写。
备注:Dockerfile 是一个文本文件,它没有文件扩展名。它就是名为 “Dockerfile” 的文件(注意 D 是大写的)。这里Dockerfile是约定俗成的,当然也可以改名字,但是需要加参数-f
然后在腾讯云上输入:sudo docker-compose up
然后等待一段时间,会出现

这时候你的服务就部署成功了,访问http://ip:5000就可以看到web已经成功执行。

对于有些第一次访问不成功的,可以在安全组里放出5000端口
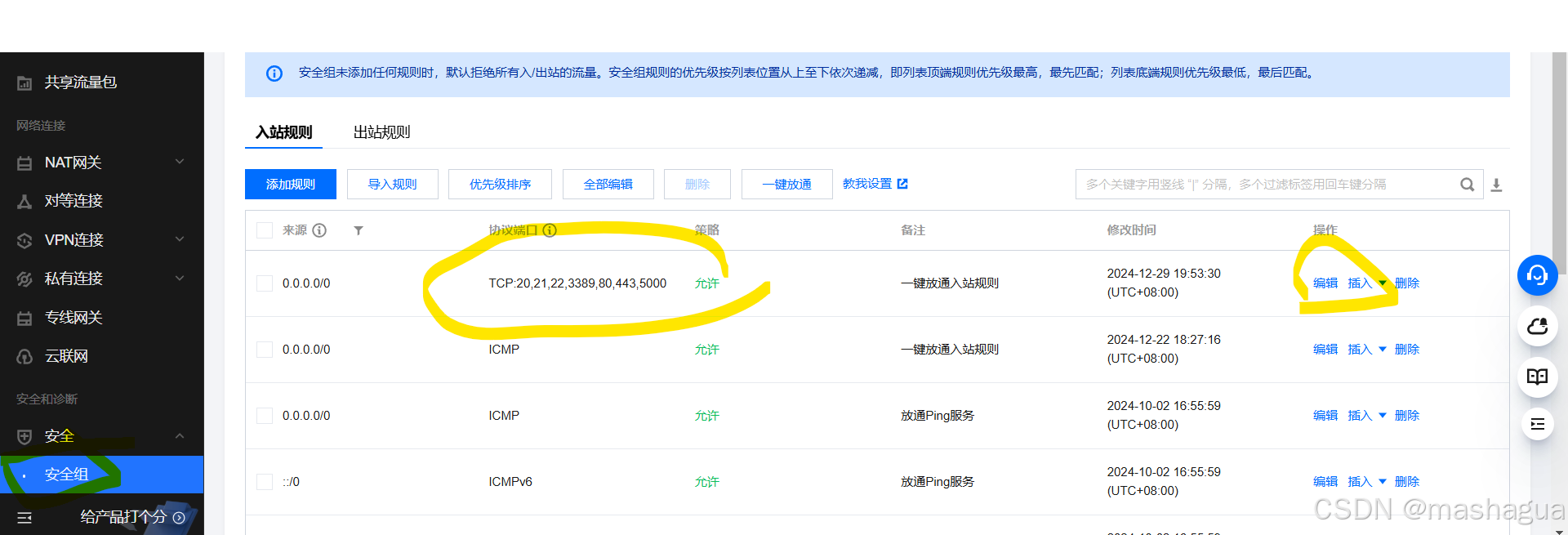
然后刷新网页就可以访问了。
一些常用的docker 命令:
-
列出所有容器(包括停止的):
docker ps -a -
列出正在运行的容器:
docker ps -
启动一个已停止的容器:
docker start my_container -
停止一个正在运行的容器:
docker stop my_container -
删除一个容器:
docker rm my_container -
进入一个正在运行的容器:
docker exec -it my_container /bin/bash -
查看容器的日志:
docker logs my_container镜像操作
-
列出所有镜像:
docker images -
拉取一个镜像:
docker pull nginx -
删除一个镜像:
docker rmi nginx -
构建一个镜像:
docker build -t my_image:latest .-t my_image:latest:指定镜像名称和标签.:Dockerfile 所在的目录
-
查看镜像的历史记录:
docker history my_image:latest
网络操作
-
列出所有网络:
docker network ls -
创建一个新的网络:
docker network create my_network -
删除一个网络:
docker network rm my_network -
查看网络的详细信息:
docker network inspect my_network卷操作
-
列出所有卷:
docker volume ls -
创建一个新的卷:
docker volume create my_volume -
删除一个卷:
docker volume rm my_volume -
查看卷的详细信息:
docker volume inspect my_volume
系统操作
-
清理未使用的资源:
docker system prune- 删除所有未被使用的容器、网络、卷和镜像。
- 加上
-a或--all选项可以删除所有资源(包括正在使用的):docker system prune -a
-
查看 Docker 信息:
docker info -
查看 Docker 版本:
docker version
其他常用命令
-
查看 Docker 帮助文档:
docker --help -
查看某个 Docker 命令的帮助文档:
docker run --help
相关文章:

Docker新手:在tencent云上实现Python服务打包到容器
1 使用docker的原因 一致性和可移植性:Docker 容器可以在任何支持 Docker 的环境中运行,无论是开发者的笔记本电脑、测试服务器还是生产环境。这确保了应用在不同环境中的行为一致,减少了“在我的机器上可以运行”的问题。 隔离性ÿ…...

React基础知识学习
学习React前端框架是一个系统而深入的过程,以下是一份详细的学习指南: 一、React基础知识 React简介 React是一个用于构建用户界面的JavaScript库,由Facebook开发和维护。它强调组件化和声明式编程,使得构建复杂的用户界面变得更…...
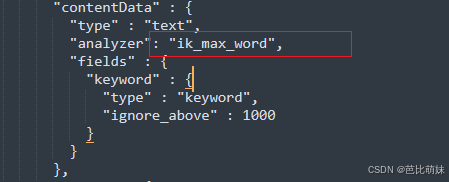
ES IK分词器插件
前言 ES中默认了许多分词器,但是对中文的支持并不友好,IK分词器是一个专门为中文文本设计的分词工具,它不是ES的内置组件,而是一个需要单独安装和配置的插件。 Ik分词器的下载安装(Winows 版本) 下载地址:…...

二十三种设计模式-抽象工厂模式
抽象工厂模式(Abstract Factory Pattern)是一种创建型设计模式,它提供了一种方式,用于创建一系列相关或相互依赖的对象,而不需要指定它们具体的类。这种模式主要用于系统需要独立于其产品的创建逻辑时,并且…...
python opencv的orb特征检测(Oriented FAST and Rotated BRIEF)
官方文档:https://docs.opencv.org/4.10.0/d1/d89/tutorial_py_orb.html SIFT/SURF/ORB对比 https://www.bilibili.com/video/BV1Yw411S7hH?spm_id_from333.788.player.switch&vd_source26bb43d70f463acac2b0cce092be2eaa&p80 ORB代码 import numpy a…...
高阶数据结构----布隆过滤器和位图
(一)位图 位图是用来存放某种状态的,因为一个bit上只能存0和1所以一般只有两种状态的情况下适合用位图,所以非常适合判断数据在或者不在,而且位图十分节省空间,很适合于海量数据,且容易存储&…...
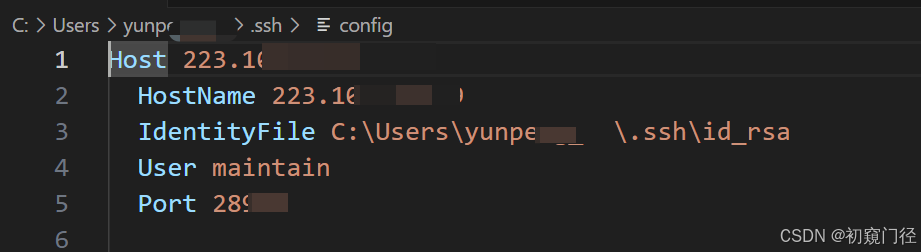
VScode使用密钥进行ssh连接服务器方法
如何正常连接ssh的方式可以看我原来那篇文章:Windows上使用VSCode连接远程服务器ssh 1.连接 点击ssh加号,然后关键点在第2步的书写上 2.命令 2的位置写命令: ssh -i "C:\Users\userName\.ssh\id_rsa" usernameIP -p 端口号 端…...
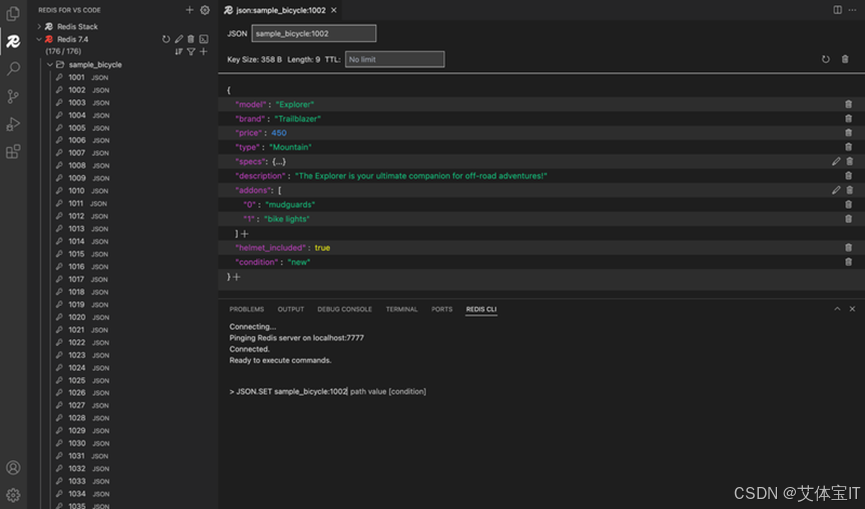
艾体宝产品丨加速开发:Redis 首款 VS Code 扩展上线!
Redis 宣布推出其首款专为 VS Code 设计的 Redis 扩展。这一扩展将 Redis 功能直接整合进您的集成开发环境(IDE),旨在简化您的工作流程,提升工作效率。 我们一直致力于构建强大的开发者生态系统,并在您工作的每一步提…...
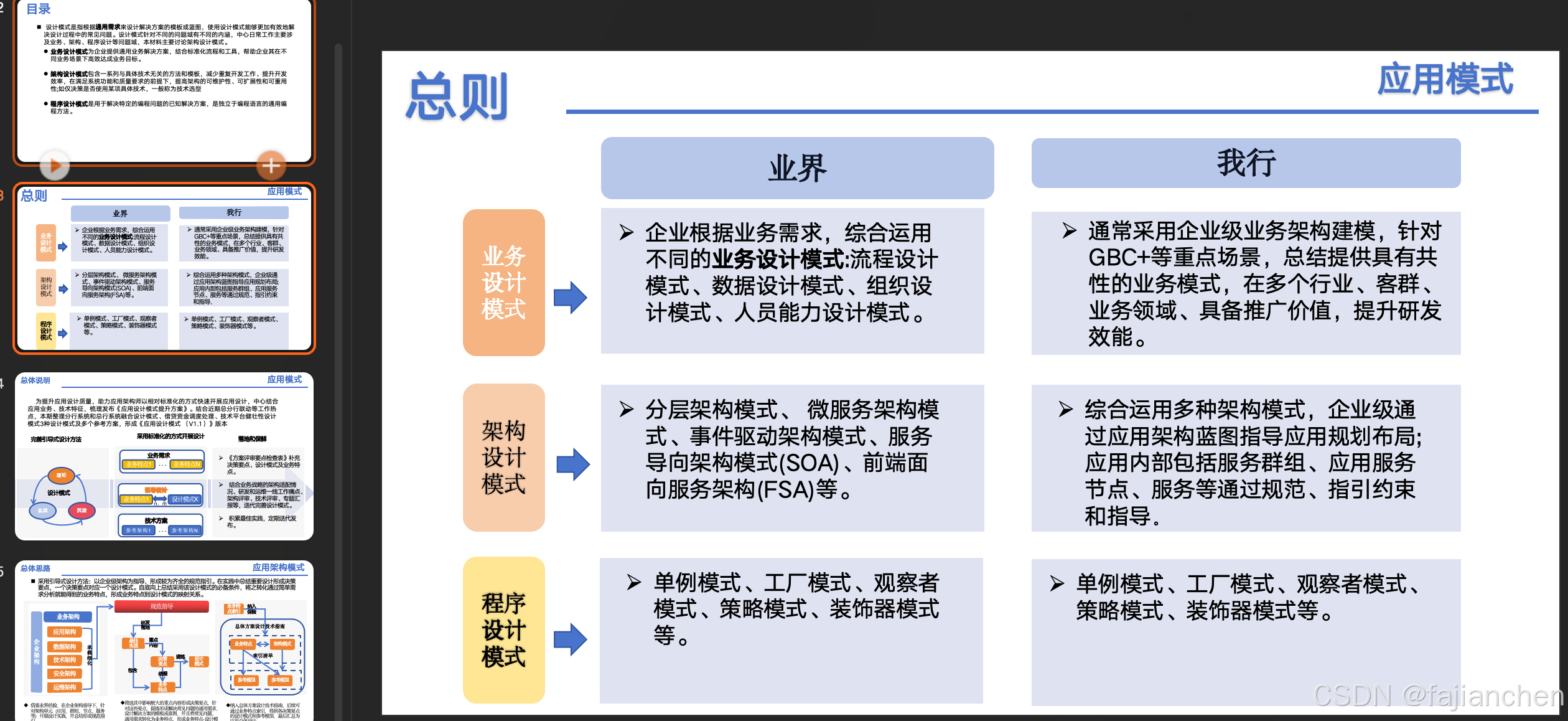
应用架构模式
设计模式 设计模式是指根据通用需求来设计解决方案的模板或蓝图,使用设计模式能够更加有效地解决设计过程中的常见问题。设计模式针对不同的问题域有不同的内涵,主要涉及业务、架构、程序设计等问题域,本文主要讨论架构设计模式。 业务设计模…...

注入少量可学习的向量参数: 注入适配器IA3
注入少量可学习的向量参数: 注入适配器IA3 简介:IA3通过学习向量来对激活层加权进行缩放,从而获得更强的性能,同时仅引入相对少量的新参数。它的诞生背景是为了改进LoRA,与LoRA不同的是,IA3直接处理学习向量,而不是学习低秩权重矩阵,这使得可训练参数的数量更少,并且原…...

【C++】B2076 球弹跳高度的计算
博客主页: [小ᶻ☡꙳ᵃⁱᵍᶜ꙳] 本文专栏: C 文章目录 💯前言💯题目描述输入格式输出格式输入输出示例 💯两种代码实现及其对比我的代码实现代码分析优点与不足 老师的代码实现代码分析优点与不足 💯两种实现的对…...
)
【Python】selenium结合js模拟鼠标点击、拦截弹窗、鼠标悬停方法汇总(使用 execute_script 执行点击的方法)
我们在写selenium获取网络信息的时候,有时候我们会受到对方浏览器的监控,对方通过分析用户行为模式,如点击、滚动、停留时间等,网站可以识别出异常行为,进而对Selenium爬虫进行限制。 这里我们可以加入JavaScript的使…...

CatBoost算法详解与PyTorch实现
CatBoost算法详解与PyTorch实现 目录 CatBoost算法详解与PyTorch实现@[TOC](目录)1. CatBoost算法概述1.1 梯度提升树(GBDT)1.2 CatBoost的优势2. CatBoost的核心技术2.1 类别特征处理2.2 对称树结构2.3 有序提升技术2.4 正则化技术3. PyTorch实现CatBoost3.1 环境准备3.2 Py…...

“TypeScript版:数据结构与算法-初识算法“
引言 在算法与编程的广阔世界里,总有一些作品以其独特的魅力和卓越的设计脱颖而出,成为我们学习和研究的典范。今天,我非常荣幸地向大家分享一个令人印象深刻的算法——Hello算法。 Hello算法不仅展现了作者深厚的编程功底,更以…...

mysql中递归的使用 WITH RECURSIVE
MySQL递归查询的基本语法和用法 MySQL 8.0及以上版本支持使用WITH RECURSIVE来进行递归查询。WITH RECURSIVE定义了一个递归的公用表表达式(CTE),它包含两个部分:递归的基础部分(非递归部分)和递归部分。 …...

点击取消按钮,console出来数据更改了,页面视图没有更新
点击取消按钮,console出来数据更改了,页面视图没有更新 前言 实现效果:点击取消按钮,页面视图全部为空, 遇到的问题: 点击取消按钮,console出来数据更改了,SchemaJson 都是默认值啦…...

web框架在什么程度上受限 ?
Web框架提供了开发网站和Web应用的基础结构和工具,但它们也有一些限制。了解这些限制有助于选择合适的框架或决定何时可能需要寻找或开发替代方案。 1、问题背景 提问者计划构建一个 RESTful web 服务,该服务将只使用 JSON/XML 接口,不包含 …...

实践:事件循环
实践:事件循环 代码示例 console.log(1); setTimeout(() > console.log(2), 0); Promise.resolve(3).then(res > console.log(res)); console.log(4);上述的代码的输出结果是什么 1和4肯定优先输出,因为他们会立即方式堆栈的执行上下文中执行&am…...
)
C++ 设计模式:建造者模式(Builder Pattern)
链接:C 设计模式 链接:C 设计模式 - 工厂方法 链接:C 设计模式 - 抽象工厂 链接:C 设计模式 - 原型模式 建造者模式(Builder Pattern)是一种创建型设计模式,它允许你分步骤创建复杂对象。与其他…...

SQL偏移类窗口函数—— LAG()、LEAD()用法详解
SQL偏移类窗口函数:LAG() 和 LEAD() 用法详解 在 SQL 中,偏移类窗口函数 LAG() 和 LEAD() 用于访问当前行的前几行或后几行的值。 1. LAG() 函数 LAG() 函数返回当前行的前几行的数据。 LAG(Expression, OffSetValue, DefaultVar) OVER (PARTITION BY …...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
