概率论与数理统计
概率论占比更多,三分之二左右
数理统计会少一些
事件之间的概率

![]() ab互斥,不是ab独立
ab互斥,不是ab独立


古典概型吃高中基础,考的不会很多
条件概率公式,要记


公式不要全记,很多有名称的公式是通过基础公式转换而来的
目的在于解决一些问题的解决经常需要相同的一套流程
所以干脆在这个基础上直接转换出流程的公式


随机变量X的分布
一维随机变量及其分布,,这一章很重要,而且是后续学习的理论基础


有很多的离散分布类型,重点部分为二项分布和泊松分布




均匀分布和指数分布


连续这一块有正态分布,正态分布很重要,贯穿后面的数理统计

对于这个公式的考察,概率不大

正态分布使用之前要先转换为标准化变量,才方便计算

离散型函数

一般还是考连续型

单调函数y=g(x)

二维随机变量分布
联合密度函数,两个随机变量之间满足的二重积分关系
正则性,联合密度函数的区域面积为1,求出k的未知数
求出k之后,f(x,y)这个二维随机变量的函数就确认了,然后就用x+y<=4限制的区间对函数的积分范围进行限制

边缘分布,则是只观察这个二维随机变量函数的其中一个是怎么变化的



条件分布


二维联合分布、密度函数的独立性


卷积公式,z=x+y,密度函数的相加

最值的函数,即在该点的情况下,max的值为多个随机变量中最大或最小的那个F()概率

(各个随机变量互相独立,而且同概率分布函数)

随机变量的数字特征

对于概率密度连续函数--期望的求解

对于方差,一维连续分布


---切比雪夫不等式,游离知识体系外(考察较少,如果要使用也一般会直接说明)


***背***常用分布的期望和方差(连续型中的各种概率分布)

告诉一个具体的分布类型,然后求期望和方差,运用上面的公式

--二项分布中的npq算连续型方差,p是成功的概率,q是失败的概率,p+q=1
<<<<<<<<<
二维分布的特征数


协方差(只在二维的随机变量情况下)

相关系数底下的两个是标准差的意思,是两个随机变量的方差的根号相乘,

相比于协方差的求法,协方差的性质更重要

方差,协方差都是可以乘法分配律使用的


<<<<<<<<<<<<<<<<<<
大数定律与中心极限定理(过于数学化,反而考察内容较少)但出题是会出题的
大数定理--记形,变量均值->期望均值(求)

中心极限定理


<<<<<<<<<<<<<<<<<6、7、8章
数理统计
(至少是三四十分的情况)
统计量的概念,,对于一个统计量,最常见的就是这个统计量的均值和方差

多个样本共同的均值和方差


三大抽样分布的出题>>给你一个奇奇怪怪的统计量,然后可以变成三大抽样分布
>>>>>>>>>>>>>>>>>>>>>>>>>.

配出常数c,使得c*统计量Y结果服从卡方分布

t分布,参与构成t分布,需要x和y两个统计量一个满足标准正态分布,一个满足卡方分布
然后这两个分布里用的数据尽量不要重合--为了可以让两个统计量有独立的信息提供

F分布---F(1,2)两个数是两个独立统计量x和y的自由度
t分布是一个标准正态一个卡方
f分布是一个卡方加另一个一个卡方

对于标准正态分布的xi,均值和方差s方,可以满足另一些式子
在其中抽样,配凑

<<<<<<<<<<<<<<<<<<<<
数理统计,第七章,参数估计
是估计,也就是说是一种数据量稀少的情况下,要用什么方法还可以得出下一个未知量的结果
包括的知识点----点估计,估计优良性标准,区间估计
矩估计
![]() 是已给的常数,不是一个新的变量
是已给的常数,不是一个新的变量


写个 ^ 是为了表示这是估计出来的量
最大似然估计


例题

优良性标准

这个例题,第一问利用了样本量估计的无偏估计量等于期望
第二问利用了有效性的方差比较,(对于相合性一般不考察)

区间估计

在第一步,统计量的选择是一个小步骤
如何选择呢

对例题的解

这里的T分布,因为标准差未知,所以使用
判断已知哪些量----选择合适的代换式t,还是卡方,还是标准正态
额外的练习---区间估计也差不多只考这种题了

<<<<<<<<<<<<<<<<
终于也是来到了最后一章,假设检验,但这章似乎只考一个式子,好像是个大题
和上一章的参数估计有着千丝万缕的联系
--
随机变量X的分布函数中含有未知参数θ
--建立假设H0,--背择假设H1
“检验![]() 是否等于10”----不等于则为背择假设
是否等于10”----不等于则为背择假设


对于假设,会抽多个样本出来进行判断,
原假设正确,但是样本量计算结果在拒绝域
原假设错误,拒绝域的假设正确,但样本量计算结果在原假设的区间
第一类错误的概率更常用一些,显著性水平(but no care)




总体 X 不一定要服从正态分布才能使用置信区间

置信度,是只要处在 相信的可能数值区间,就算相信,的概率
先设置区间,然后才得出了这个区间的置信度

置信区间的估计是针对某个统计量(如样本均值、样本比例等),目的是为了估计总体参数的可能范围。

在 X 的正态概率密度曲线 中,从均值到置信的边界的那一段距离,而这段距离有表可以查出来,一一对应

z可以说是概率密度曲线中的一个特殊的点,而这个点减去均值,才是置信区间的长度

无偏估计量是指通过样本数据(如样本均值、样本方差等)对总体参数进行估计时,所得到的估计量的期望值恰好等于总体参数的真实值。

 两个无偏估计。。。。
两个无偏估计。。。。
、





指数分布的期望和方差



先定义了分布类型,再讲述概率分布和概率密度函数两种曲线形式
最大似然估计的目的是估计统计模型中的未知参数。具体来说,给定某种假设的统计模型和一组样本数据,最大似然估计通过最大化似然函数来估计模型中的参数。


对数似然函数:为了便于计算和优化,通常我们使用似然函数的对数,即对数似然函数(log-likelihood function)。对数似然函数是似然函数的自然对数:

假设检验需要选择统计量

需要先建立统计量模型
满足t分布之后,具体的信息会给表
--------
显著性水平(α)是指在零假设 H0H_0H0 为真的情况下,拒绝零假设的概率。具体来说,α代表的是发生第一类错误(即错误地拒绝了正确的零假设)的概率。通常,显著性水平设为 0.05 意味着,如果零假设 H0 为真,那么有 5% 的概率会错误地拒绝 H0。

相关文章:

概率论与数理统计
概率论占比更多,三分之二左右 数理统计会少一些 事件之间的概率 ab互斥,不是ab独立 古典概型吃高中基础,考的不会很多 条件概率公式,要记 公式不要全记,很多有名称的公式是通过基础公式转换而来的 目的在于解决一…...

统信系统设置代理的问题
统信系统设置代理的问题 问题表现方式一方式二 问题表现 统信系统下有系统代理和应用代理两个代理。设置系统代理时,git不能经过代理拉取代码。但是设置应用代理时,可以用git通过代理拉代码。 这是系统代理,在这里设置 ip 端口,…...

TCP 为什么采用三次握手和四次挥手以及 TCP 和 UDP 的区别
1. TCP 为什么采用三次握手和四次挥手 采用三次握手的原因: 确认双方的收发能力。第一次握手,客户端发送 SYN 报文,告诉服务器自身具备发送数据的能力,第二次握手,服务器回应 SYN ACK 报文,表名自己既能…...

springboot配置并使用RestTemplate
目录 一、RestTemplate配置 1、将RestTemplate初始化为Bean 2、使用HttpClient作为RestTemplate客户端 (1)引入HttpClient依赖 (2)修改RestTemplate配置类 3、设置拦截器 (1)新增拦截器类 …...

人工智能-Python网络编程-TCP
1 TCP-概念版 服务端 import socket # 1 创建服务端套接字对象 # socket.AF_INET IPV4 # socket.SOCK_STREAM TCP # socket.SOCK_DGRAM UDP tcp_server_socket socket.socket(socket.AF_INET, socket.SOCK_STREAM) # 2 绑定端口号 tcp_server_socket.bind((192.…...

【Java回顾】Day3 继承|Override/Ovverload|多态|抽象类|封装|接口|枚举
学习资料 菜鸟教程 https://www.runoob.com/java/java-interfaces.html 继承|Override/Ovverload|多态|抽象类|封装|接口|枚举 继承 创建分等级层次的类,子类继承父类的特征、行为、方法 class 父类{ } class 子类 extends 父类{ super(); }一些性质 Java 不支持…...

SpringMVC(四)响应
目录 数据处理及跳转 1. 结果跳转方式 ①.ModelAndView ②.ServletAPI 1、通过HttpServletResponse进行输出 2、通过HttpServletResponse实现请求转发 3、通过HttpServletResponse实现重定向 ③.SpringMVC 1.直接输出 2.请求转发 3.重定向 2.ResponseBody响应json数…...

vim 的基础使用
目录 一:vim 介绍二:vim 特点三:vim 配置四:vim 使用1、vim 语法格式2、vim 普通模式(1)保存退出(2)光标跳转(3)文本删除(4)文本查找&…...

关于flinkCDC监控mysql binlog时,datetime类型自动转换成时间戳类型问题
flinkCDC监控mysql binlog时,datetime类型自动转换成时间戳类型 问题解决1.自定义转换器类2.代码引用 结果 问题 flink版本:1.18.1,mysql版本:8.0.40 使用FlinkCDC的MySqlSource 连接mysql,对于datetime 类型字段&…...

基于Springboot校园失物招领系统【附源码】
基于Springboot校园失物招领系统 效果如下: 系统登陆页面 物品页面 系统首页面 失物招领管理页面 失物认领页面 宣传视频页面 物品挂失留言管理页面 宣传视频类型管理页面 研究背景 在校园环境中,失物招领是一个常见的问题。传统的失物招领方式主要依…...

单片机端口操作和独立引脚操作
单片机端口操作和独立引脚操作 在单片机编程中,控制I/O端口是最基础的操作之一。通过控制端口,我们可以实现对外设(如LED、按键、继电器等)的控制。在51单片机中,有两种常见的端口操作方式:整体控制&#…...

【Vim Masterclass 笔记03】S03L10 + S03L11:Vim 中的文本删除操作以及 Vim 思维习惯的培养(含 DIY 拓展知识点)
文章目录 Section 3:Vim Essentials(Vim 核心知识)S03L10 Vim 核心浏览命令同步练习点评课S03L11 Deleting Text and "Thinking in Vim" 文本的删除及 Vim 思维习惯的培养1 删除单个字符2 删除一个单词2.1 推广1:D HJK…...

ARM200~500部署
前提:数据库已经安装好,并且正常运行 1.修改hostname,将里面的AR-A 改为hzx vi /etc/hostname 2.重启网络服务 sudo systemctl restart NetworkManager 3.修改community-admin.service 文件,更改小区名称和IP,并将文件上传到/…...

word中插入zotero引用
1、参考文献末尾没有文献? 在文献条目要显示的地方点击“refresh” 2、参考文献条目没有悬挂缩进? 把“书目”添加到样式库中,修改样式为悬挂缩进1.5字符 3、交叉引用? 宏 新建一个宏 粘贴下面代码 Public Sub ZoteroLinkCita…...

需求上线,为什么要刷缓存?
在需求上线的过程中,刷缓存主要有以下几个重要原因: 一、保证数据的准确性 旧数据残留问题 缓存是为了加快数据访问速度而存储的数据副本。在需求更新后,之前缓存中的数据可能已经不符合新的业务逻辑。例如,一个电商网站修改了商…...

TVS二极管选型【EMC】
TVS器件并联在电路中,当电路正常工作时,他处于截止状态(高阻态),不影响线路正常工作,当线路处于异常过压并达到其击穿电压时,他迅速由高阻态变为低阻态,给瞬间电流提供一个低阻抗导通…...

《从入门到精通:蓝桥杯编程大赛知识点全攻略》(一)-递归实现指数型枚举、递归实现排列型枚举
本篇博客将聚焦于通过递归来实现两种经典的枚举方法:指数型枚举和排列型枚举。这两种枚举方式在计算机科学和算法竞赛中都有广泛应用,无论是在解题中,还是在实际工作中都极具价值。 目录 前言 斐波那契数列递归 递归实现指数型枚举 算法思…...

C#对线程同步的应用
什么是线程同步?线程同步的应用场景有哪些?在C#中有哪些线程同步方式?下面对这些问题做一个总结,让大家在面试的时候遇到这些问题能够游刃有余。 线程同步是指在多线程环境下,多个线程同时访问共享资源时,确…...

基于微信小程序的面部动作检测系统
引言 本技术文档旨在详细阐述一个基于微信小程序的面部动作检测系统的技术路线、实现方法及关键技术框架。系统的核心功能包括检测用户的左右转头、眨眼和张嘴动作,并根据检测结果逐步引导用户完成任务。为确保系统的安全性和准确性,特别是防止用户通过…...
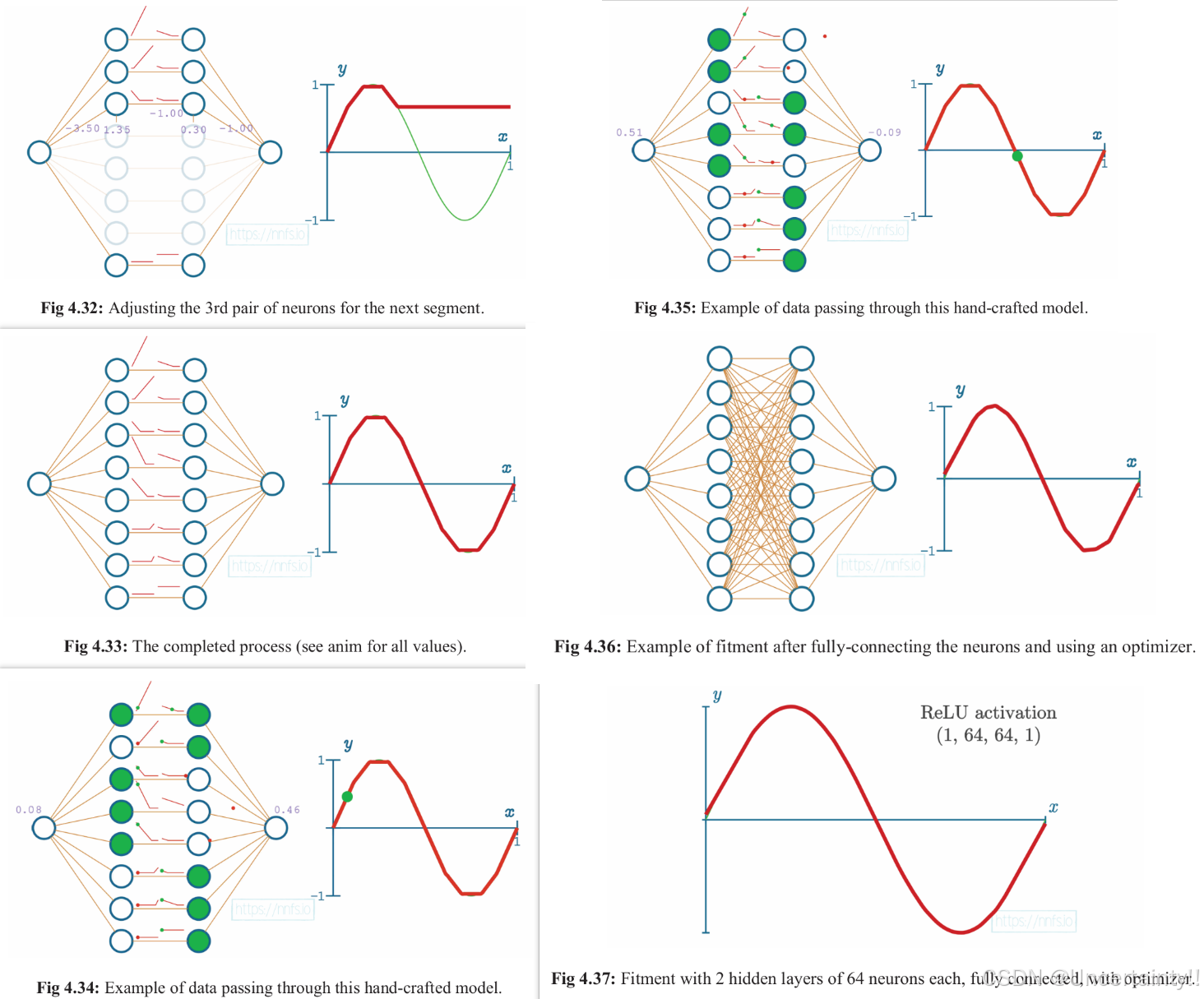
Activation Functions
Chapter4:Activation Functions 声明:本篇博客笔记来源于《Neural Networks from scratch in Python》,作者的youtube 其实关于神经网络的入门博主已经写过几篇了,这里就不再赘述,附上链接。 1.一文窥见神经网络 2.神经…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
