《从入门到精通:蓝桥杯编程大赛知识点全攻略》(一)-递归实现指数型枚举、递归实现排列型枚举
本篇博客将聚焦于通过递归来实现两种经典的枚举方法:指数型枚举和排列型枚举。这两种枚举方式在计算机科学和算法竞赛中都有广泛应用,无论是在解题中,还是在实际工作中都极具价值。
目录
前言
斐波那契数列递归
递归实现指数型枚举
算法思路
代码如下
递归实现排列型枚举
算法思路
代码如下
总结
前言
在编程的世界里,递归是一种优雅且强大的技术,它能让复杂问题变得更加简洁和易于理解。无论是数学中的公式推导,还是计算机科学中的算法设计,递归都扮演着不可或缺的角色。在数据结构与算法中,递归不仅能帮助我们高效地解决问题,还能展现出代码的简洁性和表达力。
本篇博客将聚焦于通过递归来实现两种经典的枚举方法:指数型枚举和排列型枚举。这两种枚举方式在计算机科学和算法竞赛中都有广泛应用,无论是在解题中,还是在实际工作中都极具价值。
斐波那契数列递归

递归最经典的就是斐波那契数列,其中第1个数是1,第2个数是2,第3个数是前两个数字之和。

java代码如下:
package AcWingLanQiao;import java.util.*;public class 递归 {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();System.out.println(f(n));}public static int f(int n){if(n==1){ return 1;}if(n==2){ return 2;}return f(n-1)+f(n-2);}
}

递归实现指数型枚举
从 1∼n 这 n 个整数中随机选取任意多个,输出所有可能的选择方案。
输入格式
输入一个整数 n。
输出格式
每行输出一种方案。
同一行内的数必须升序排列,相邻两个数用恰好 1 个空格隔开。
对于没有选任何数的方案,输出空行。
数据范围
1≤n≤15
输入样例
3输出样例
3
2
2 3
1
1 3
1 2
1 2 3算法思路

每一个位置都有两种情况,分别是选和不选。
当有n个数时,结果就有中情况。

当n为对的时候,上述对应的是递归搜索树。从第一个位置开始分两种情况,选和不选,后续每个位置一次类推。
我们用一个数组flag,数组下标表示从1到n,flag[i]表示该值在每个位置的状态,0表示还未考虑,1表示选,2表示这个位置不选;通过dfs深度优先搜索,用u来表示当前在哪个位置,先思考递归的出口,当当前位置u要大于n时(即u > n),就说明n个位置每个位置的情况都处理好了,就说明最后flag[i] = 1对应的下标就是结果所需的序列。
当u <= n时,我们只需处理两种情况,一种是选,一种是不选。当选时,将flag[u] = 1,然后递归的处理下一个位置dfs(u+1),最后再恢复现场flag[u] = 0,即相当于是当前的位置都处理完了,将位置恢复为未处理,然后再走另一种情况;当不选时,将flag[u] = 2,后递归的处理下一个位置dfs(u+1),最后再恢复现场flag[u] = 0。
代码如下
package AcWingLanQiao;
import java.io.*;
import java.util.*;public class 递归实现指数型枚举 {static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static StreamTokenizer st = new StreamTokenizer(br);static int N = 16;/*状态数据,记录每个位置的当前状态0表示还未考虑1表示选它2表示不选它*/static int[] flag = new int[N];static int n;public static void main(String[] args)throws Exception {n = nextInt();dfs(1);pw.flush();}public static void dfs(int u){if(u > n){for(int i = 1;i <= n;i++){if(flag[i] == 1){pw.print(i+" ");}}pw.println();pw.flush();return;}flag[u] = 2;dfs(u+1); //第一个分支不选flag[u] = 0;//恢复现场flag[u] = 1;dfs(u+1); //第二个分支选flag[u] = 0;}public static int nextInt() throws Exception {st.nextToken();return (int)st.nval;}
}
递归实现排列型枚举
把 1∼n 这 n 个整数排成一行后随机打乱顺序,输出所有可能的次序。
输入格式
一个整数 n。
输出格式
按照从小到大的顺序输出所有方案,每行 1 个。
首先,同一行相邻两个数用一个空格隔开。
其次,对于两个不同的行,对应下标的数一一比较,字典序较小的排在前面。
数据范围
1≤n≤9
输入样例
3输出样例
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1注:字典序排序是一种按照字典中单词出现的顺序来排列元素的方法。在计算机科学中,它被用来比较两个字符串的大小关系,即比较它们从左到右第一个不同字符的ASCII值的大小关系。这种排序方式不仅适用于英文单词,也适用于任意字符串的比较。
算法思路


用整型数组arr来存储数列的结果,布尔类型数组flag,其中flag[i]若为true表示数字i已被使用,若为false表示数字i未被使用。使用深度优先搜索dfs来解决此问题。我们可以通过每个位置放置哪个数字来进行思考。
我们先来思考递归的出口,当当前位置u大于n时(即u > n),说明所有的位置上数字都以排好,所以此时只需打印arr数组,就可以得到结果。当n为3时,说明一个位置有3种情况,所以要有一个外层循环,然后来判断flag[i]是否被使用,未被使用则将当前位置复制为i即arr[u] = i,还需将该数字对应的flage数组设置为已使用即flag[i] = true,然后递归的处理下一个位置即dfs(u+1),最后再进行回溯操作flag[i] = false。如果flag[i]已经被使用,则接着进行下一次数字进行判断,n个数字都被使用,也可说明数列已被排完序。
算法时间复杂度为O(n*n!)
代码如下
import java.io.*;public class Main {static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static StreamTokenizer st = new StreamTokenizer(br);static int N = 10;static int[] arr = new int[N];static boolean[] flag = new boolean[N]; //true表示用过 false表示未被用过static int n;public static void main(String[] args) throws IOException {n = nextInt();dfs(1);pw.flush();}public static void dfs(int u) {if(u > n){ //边界for(int i = 1; i<= n;i++){pw.print(arr[i]+" ");}pw.println();return;}//枚举每个分支for(int i = 1; i<= n;i++){if(!flag[i]){arr[u] = i;flag[i] = true;dfs(u+1);//恢复现场flag[i] = false;}}}public static int nextInt() throws IOException {st.nextToken();return (int) st.nval;}
}
代码输入
4代码输出结果
1 2 3 4
1 2 4 3
1 3 2 4
1 3 4 2
1 4 2 3
1 4 3 2
2 1 3 4
2 1 4 3
2 3 1 4
2 3 4 1
2 4 1 3
2 4 3 1
3 1 2 4
3 1 4 2
3 2 1 4
3 2 4 1
3 4 1 2
3 4 2 1
4 1 2 3
4 1 3 2
4 2 1 3
4 2 3 1
4 3 1 2
4 3 2 1 总结
通过本篇博客的学习,我们可以看到递归作为一种经典的编程技巧,不仅能够简化问题的解决过程,还能提高代码的可读性和执行效率。递归在指数型枚举和排列型枚举中的应用,展示了它在不同场景中的灵活性与强大功能。
无论是初学者还是有一定编程经验的开发者,理解并掌握递归的精髓对于解决实际问题都有很大的帮助。希望通过这篇博客,能够带给大家一些启发,并鼓励大家在实际编程过程中善于运用递归,解锁更多的编程奥秘。
相关文章:

《从入门到精通:蓝桥杯编程大赛知识点全攻略》(一)-递归实现指数型枚举、递归实现排列型枚举
本篇博客将聚焦于通过递归来实现两种经典的枚举方法:指数型枚举和排列型枚举。这两种枚举方式在计算机科学和算法竞赛中都有广泛应用,无论是在解题中,还是在实际工作中都极具价值。 目录 前言 斐波那契数列递归 递归实现指数型枚举 算法思…...

C#对线程同步的应用
什么是线程同步?线程同步的应用场景有哪些?在C#中有哪些线程同步方式?下面对这些问题做一个总结,让大家在面试的时候遇到这些问题能够游刃有余。 线程同步是指在多线程环境下,多个线程同时访问共享资源时,确…...

基于微信小程序的面部动作检测系统
引言 本技术文档旨在详细阐述一个基于微信小程序的面部动作检测系统的技术路线、实现方法及关键技术框架。系统的核心功能包括检测用户的左右转头、眨眼和张嘴动作,并根据检测结果逐步引导用户完成任务。为确保系统的安全性和准确性,特别是防止用户通过…...
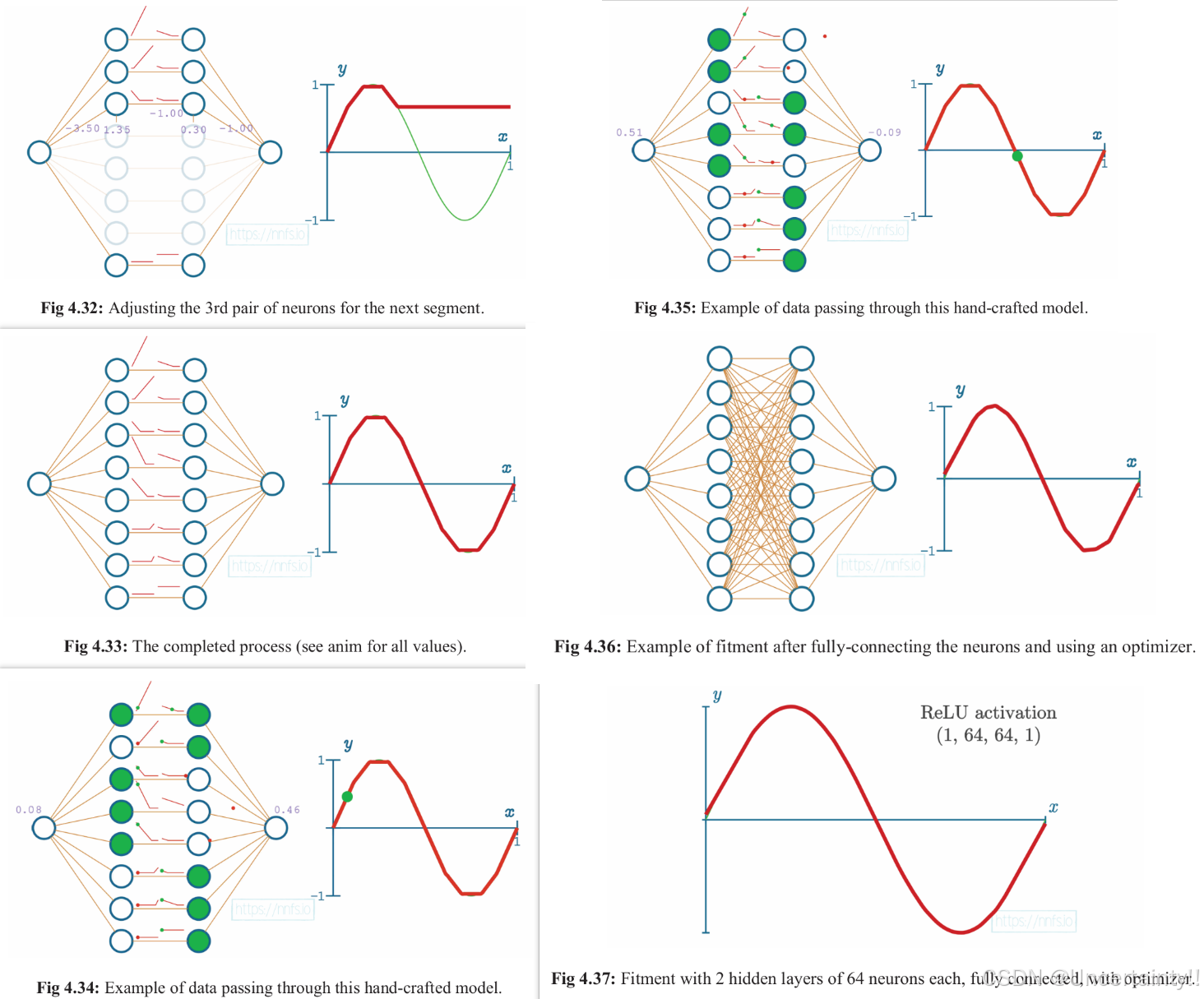
Activation Functions
Chapter4:Activation Functions 声明:本篇博客笔记来源于《Neural Networks from scratch in Python》,作者的youtube 其实关于神经网络的入门博主已经写过几篇了,这里就不再赘述,附上链接。 1.一文窥见神经网络 2.神经…...

《Vue3实战教程》37:Vue3生产部署
如果您有疑问,请观看视频教程《Vue3实战教程》 生产部署 开发环境 vs. 生产环境 在开发过程中,Vue 提供了许多功能来提升开发体验: 对常见错误和隐患的警告对组件 props / 自定义事件的校验响应性调试钩子开发工具集成 然而ÿ…...

Linux:各发行版及其包管理工具
相关阅读 Linuxhttps://blog.csdn.net/weixin_45791458/category_12234591.html?spm1001.2014.3001.5482 Debian 包管理工具:dpkg(低级包管理器)、apt(高级包管理器,建立在dpkg基础上)包格式:…...
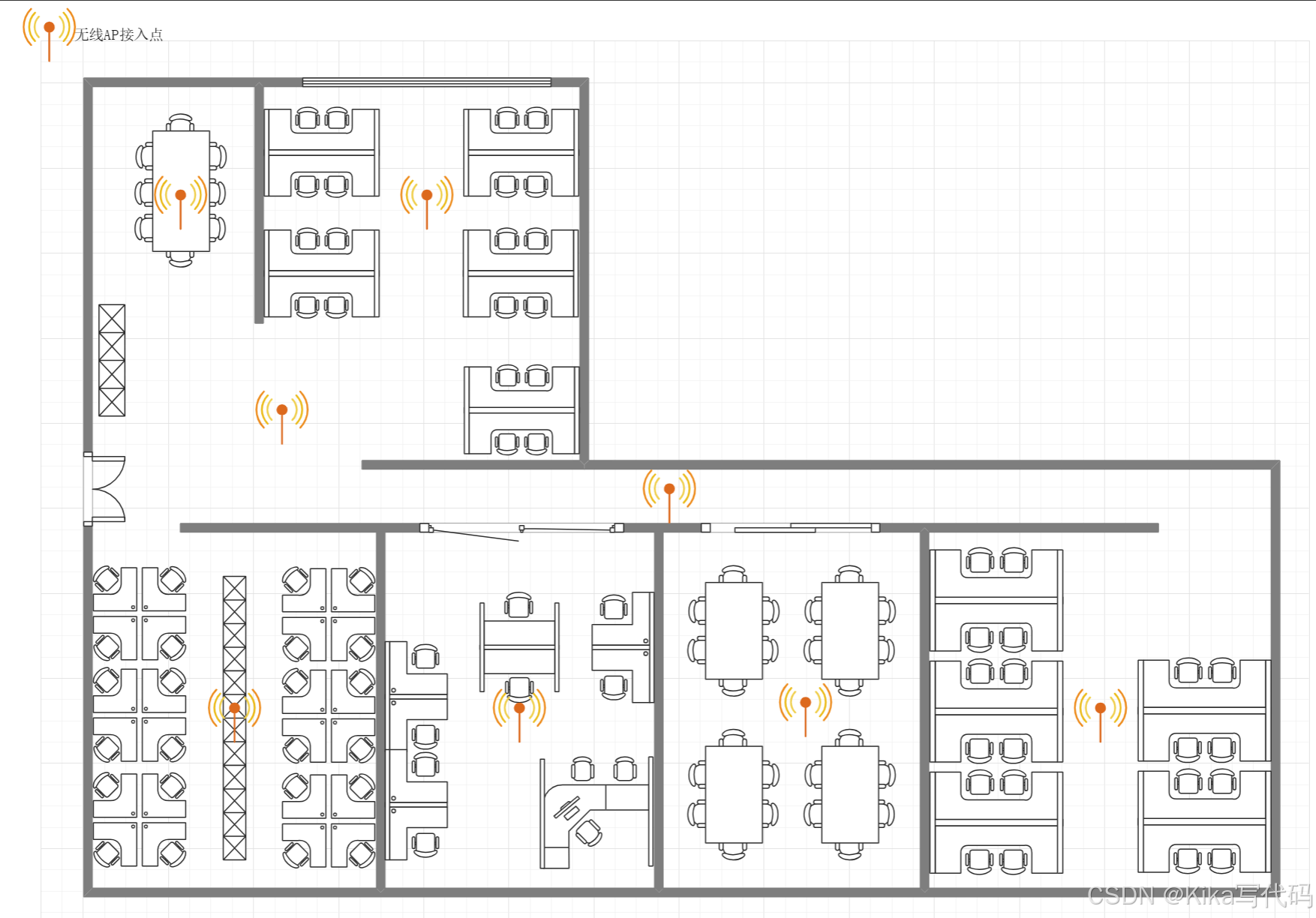
【计算机网络】课程 作业一 搭建连续覆盖的办公网络
作业一 搭建连续覆盖的办公网络 题目:论述题(共1题,100分) 充分利用所学习的数据链路层局域网知识,加上物理层的基础知识,请给一个办公场所(三层,每层约100平方)…...
)
C++ 设计模式:单例模式(Singleton Pattern)
链接:C 设计模式 链接:C 设计模式 - 享元模式 单例模式(Singleton Pattern)是创建型设计模式,它确保一个类只有一个实例,并提供一个全局访问点来访问这个实例。单例模式在需要全局共享资源或控制实例数量的…...

OpenCV调整图像亮度和对比度
【欢迎关注编码小哥,学习更多实用的编程方法和技巧】 1、基本方法---线性变换 // 亮度和对比度调整 cv::Mat adjustBrightnessContrast(const cv::Mat& src, double alpha, int beta) {cv::Mat dst;src.convertTo(dst, -1, alpha, beta);return dst; }// 使用…...
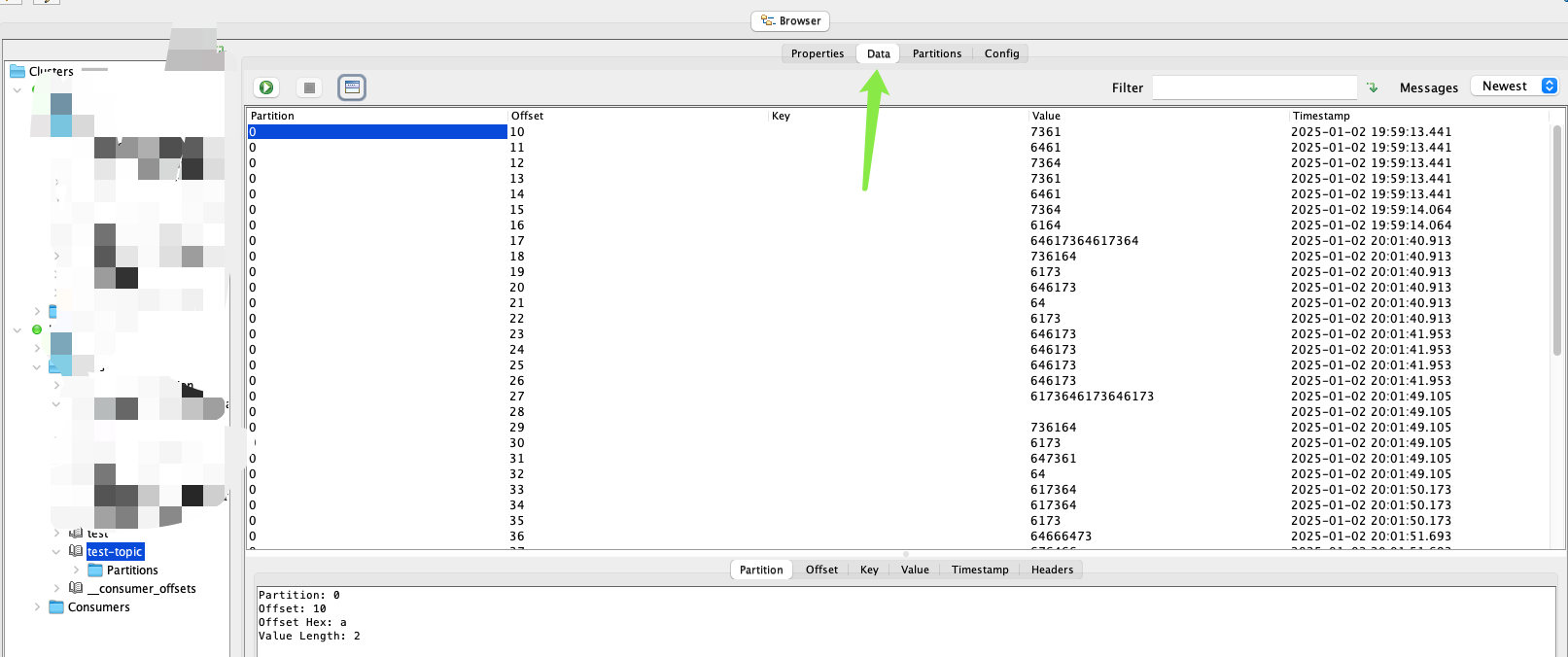
Kafka Offset explorer使用
Kafka集群配置好以后以后运维这边先用工具测试一下,便于rd展开后续的工作,本地调试时一般使用Offset explorer工具进行连接 使用SASL(Simple Authentication and Security Layer)验证方式 使用SCRAM-SHA-256(Salted Challenge Response Authentication…...
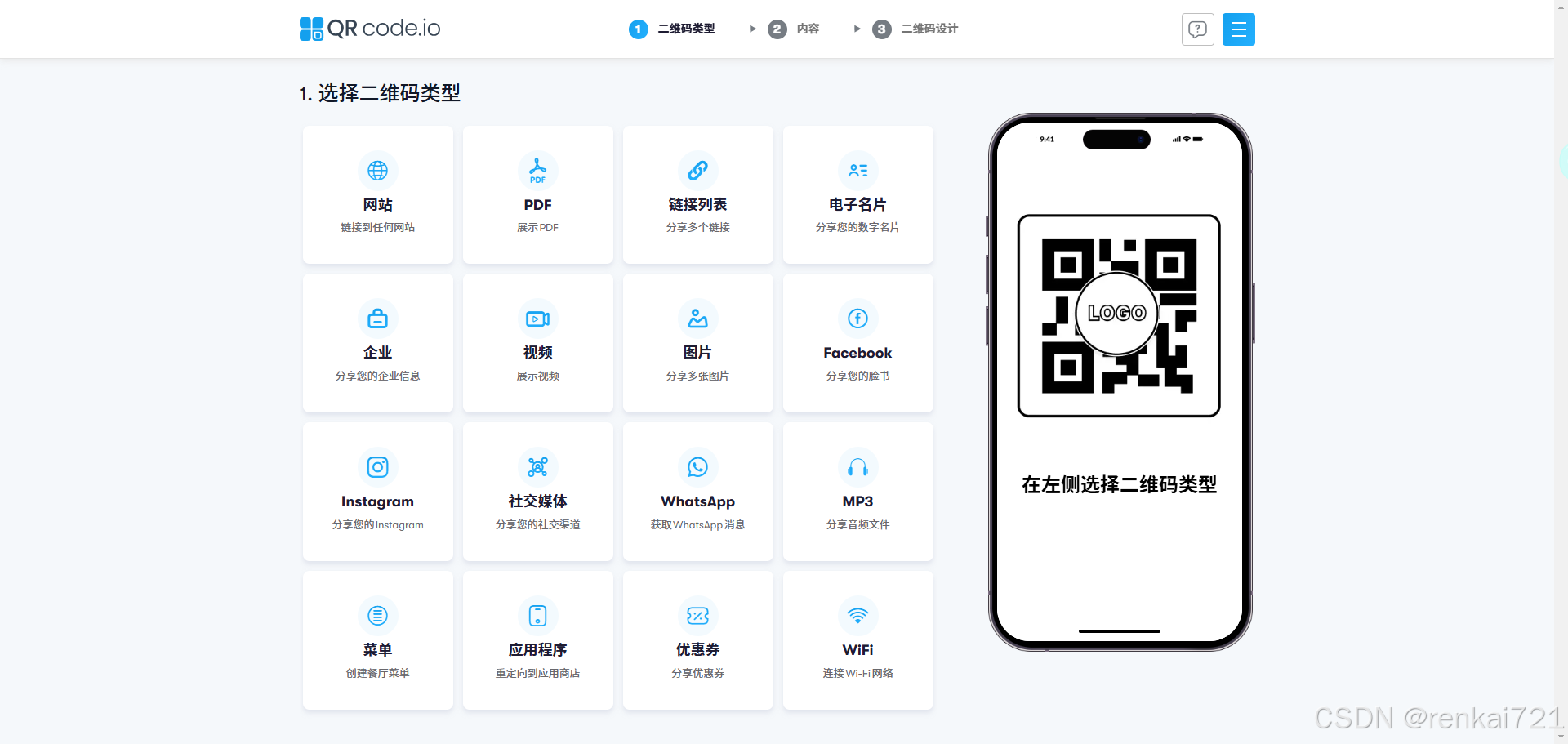
二维码文件在线管理系统-收费版
需求背景 如果大家想要在网上管理自己的文件,而且需要生成二维码,下面推荐【草料二维码】,这个系统很好。特别适合那些制造业,实体业的使用手册,你可以生成一个二维码,贴在设备上,然后这个二维码…...

UE4.27 Android环境下获取手机电量
获取电量方法 使用的方法时FAndroidMisc::GetBatteryLevel(); 出现的问题 但是在电脑上编译时发现,会发现编译无法通过。 因为安卓环境下编译时,包含 #include "Android/AndroidPlatformMisc.h" 头文件是可以正常链接的,但在电…...

vue-i18n报错
1. 开发环境报错Uncaught (in promise) TypeError: ‘set’ on proxy: trap returned falsish for property ‘$t’ legacy需要设置为false const i18n createI18n({legacy: false,// 默认语言locale: lang,// 设置语言环境messages, })2. 打包配置tsc --noEmit时报错&#…...
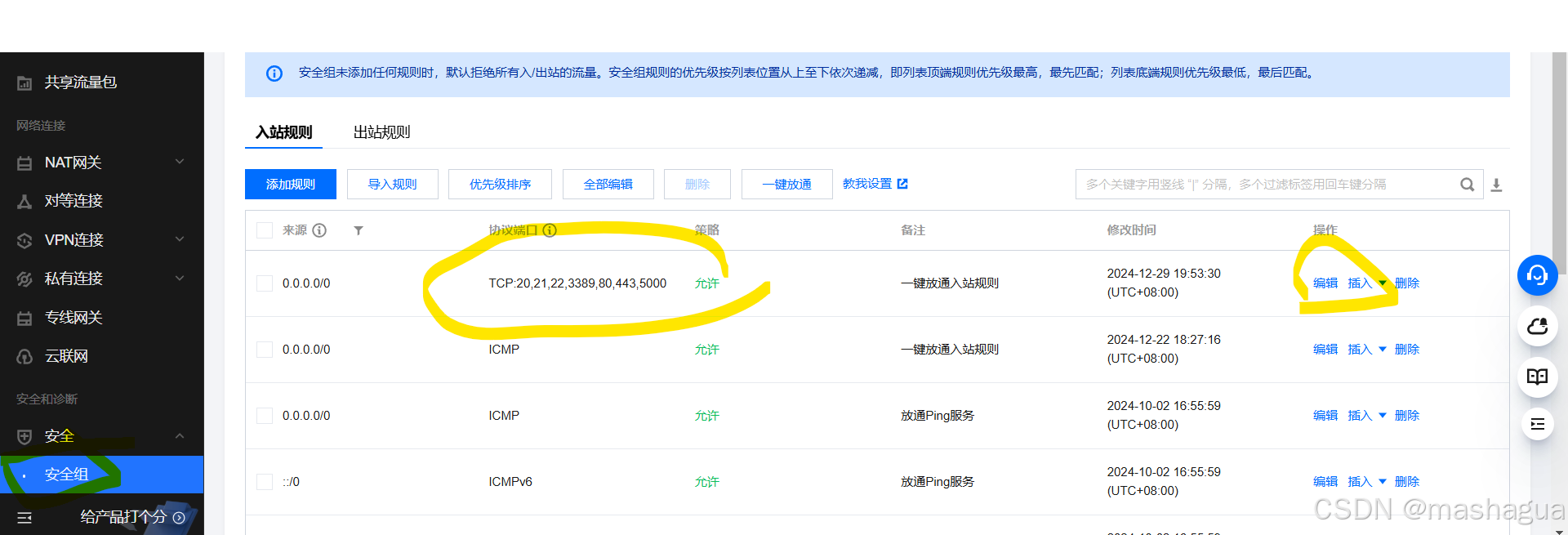
Docker新手:在tencent云上实现Python服务打包到容器
1 使用docker的原因 一致性和可移植性:Docker 容器可以在任何支持 Docker 的环境中运行,无论是开发者的笔记本电脑、测试服务器还是生产环境。这确保了应用在不同环境中的行为一致,减少了“在我的机器上可以运行”的问题。 隔离性ÿ…...

React基础知识学习
学习React前端框架是一个系统而深入的过程,以下是一份详细的学习指南: 一、React基础知识 React简介 React是一个用于构建用户界面的JavaScript库,由Facebook开发和维护。它强调组件化和声明式编程,使得构建复杂的用户界面变得更…...
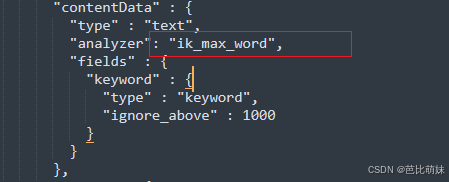
ES IK分词器插件
前言 ES中默认了许多分词器,但是对中文的支持并不友好,IK分词器是一个专门为中文文本设计的分词工具,它不是ES的内置组件,而是一个需要单独安装和配置的插件。 Ik分词器的下载安装(Winows 版本) 下载地址:…...

二十三种设计模式-抽象工厂模式
抽象工厂模式(Abstract Factory Pattern)是一种创建型设计模式,它提供了一种方式,用于创建一系列相关或相互依赖的对象,而不需要指定它们具体的类。这种模式主要用于系统需要独立于其产品的创建逻辑时,并且…...
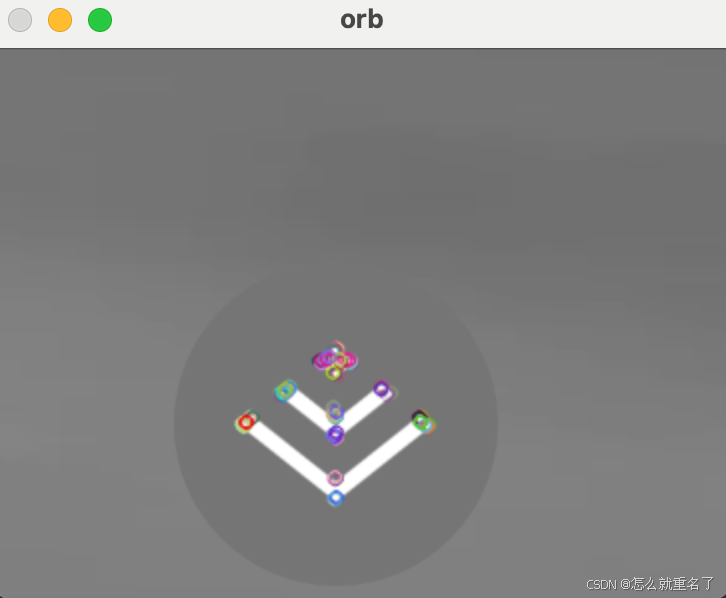
python opencv的orb特征检测(Oriented FAST and Rotated BRIEF)
官方文档:https://docs.opencv.org/4.10.0/d1/d89/tutorial_py_orb.html SIFT/SURF/ORB对比 https://www.bilibili.com/video/BV1Yw411S7hH?spm_id_from333.788.player.switch&vd_source26bb43d70f463acac2b0cce092be2eaa&p80 ORB代码 import numpy a…...
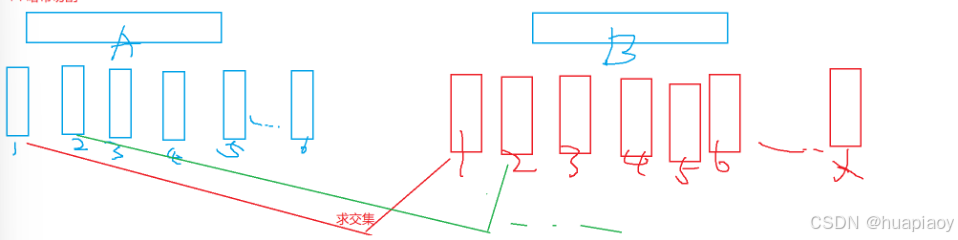
高阶数据结构----布隆过滤器和位图
(一)位图 位图是用来存放某种状态的,因为一个bit上只能存0和1所以一般只有两种状态的情况下适合用位图,所以非常适合判断数据在或者不在,而且位图十分节省空间,很适合于海量数据,且容易存储&…...
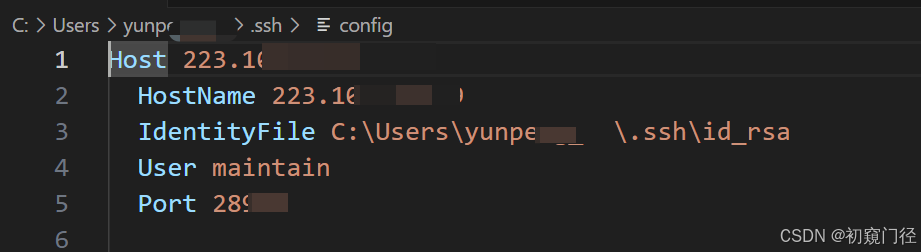
VScode使用密钥进行ssh连接服务器方法
如何正常连接ssh的方式可以看我原来那篇文章:Windows上使用VSCode连接远程服务器ssh 1.连接 点击ssh加号,然后关键点在第2步的书写上 2.命令 2的位置写命令: ssh -i "C:\Users\userName\.ssh\id_rsa" usernameIP -p 端口号 端…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
