Python贪心
贪心
- 贪心:把整体问题分解成多个步骤,在每个步骤都选取当前步骤的最优方案,直至所有步骤结束;每个步骤不会影响后续步骤
- 核心性质:每次采用局部最优,最终结果就是全局最优
- 如果题目满足上述核心性质,则可以采用贪心进行求解
如何判断是否能用贪心?
- 最优子结构性质:当一个问题的最优解包含子问题的最优解,则称之为具有最优子结构性质。
- 贪心性质选择:可以通过局部最优的选择得到全局最优
具体问题如何做?
- 经验性积累各种类型的贪心
- 举反例
经典贪心
石子合并问题
石子合并问题:每次选择最小的两个
利用堆:heapq
题目描述
在很久很久以前,有 n n n 个部落居住在平原上,依次编号为 1 1 1 到 n n n。第 i i i 个部落的人数为 t i t_i ti。
有一年发生了灾荒。年轻的政治家小蓝想要说服所有部落一同应对灾荒,他能通过谈判来说服部落进行联合。
每次谈判,小蓝只能邀请两个部落参加,花费的金币数量为两个部落的人数之和,谈判的效果是两个部落联合成一个部落(人数为原来两个部落的人数之和)。
输入描述
输入的第一行包含一个整数 n n n,表示部落的数量。
第二行包含 n n n 个正整数,依次表示每个部落的人数。
其中, 1 ≤ n ≤ 1000 , 1 ≤ t i ≤ 1 0 4 1≤n≤1000,1≤t_i≤10^4 1≤n≤1000,1≤ti≤104。
输出描述
输出一个整数,表示最小花费。
import heapq
n = int(input())
a = list(map(int, input().split()))# 把a转化为堆
heapq.heapify(a)
ans = 0
while len(a) >= 2:x = heapq.heappop(a)y = heapq.heappop(a)heapq.heappush(a, x + y)ans += x + y
print(ans)
分箱问题
每组最多两件,价值之和不超过 w w w
尽可能不浪费空间:大的和小的凑在一起
题目描述
元旦快到了,校学生会让乐乐负责新年晚会的纪念品发放工作。为使得参加晚会的同学所获得的纪念品价值相对均衡,他要把购来的纪念品根据价格进行分组,但每组最多只能包括两件纪念品,并且每组纪念品的价格之和不能超过一个给定的整数。为了保证在尽量短的时间内发完所有纪念品,乐乐希望分组的数目最少。
你的任务是写一个程序,找出所有分组方案中分组数最少的一种,输出最少的分组数目。
输入描述
第 1 1 1 行包括一个整数 w ( 80 ≤ w ≤ 200 ) w (80≤w≤200) w(80≤w≤200),为每组纪念品价格之和的上限。
第 2 2 2 行为一个整数 n ( 1 ≤ n ≤ 30000 ) n (1≤n≤30000) n(1≤n≤30000),表示购来的纪念品的总件数。
第 3 3 3~ n + 2 n+2 n+2 行每行包含一个正整数 p i ( 5 ≤ p i ≤ w ) p_i (5≤p_i≤w) pi(5≤pi≤w),表示所对应纪念品的价格。
输出描述
输出一行,包含一个整数,即最少的分组数目。
w = int(input())
n = int(input())
a = []
for i in range(n):a.append(int(input()))a.sort()
l, r = 0, n - 1
ans = 0while True:if l == r:ans += 1breakif l > r:breakif a[l] + a[r] <= w:ans += 1l += 1r -= 1else:ans += 1r -= 1
print(ans)
翻硬币问题
题目描述
小明正在玩一个"翻硬币"的游戏。
桌上放着排成一排的若干硬币。我们用 ∗ * ∗ 表示正面,用 o o o 表示反面(是小写字母,不是零)。
比如,可能情形是: ∗ ∗ o o ∗ ∗ ∗ o o o o **oo***oooo ∗∗oo∗∗∗oooo;
如果同时翻转左边的两个硬币,则变为: o o o o ∗ ∗ ∗ o o o o oooo***oooo oooo∗∗∗oooo。
现在小明的问题是:如果已知了初始状态和要达到的目标状态,每次只能同时翻转相邻的两个硬币,那么对特定的局面,最少要翻动多少次呢?
我们约定:把翻动相邻的两个硬币叫做一步操作。
输入描述
两行等长的字符串,分别表示初始状态和要达到的目标状态。
每行的长度<1000。
输出描述
一个整数,表示最小操作步数。
s = list(input())
t = list(input())
n = len(s)
ans = 0
for i in range(n):if s[i] == t[i]:continueif s[i + 1] == '*':s[i + 1] = 'o'else:s[i + 1] = '*'ans += 1
print(ans)
数组乘积问题
给定两个长度为 n n n 的正整数数组 a a a 和 b b b,可以任意排序,求 ∑ i = 1 n a [ i ] ∗ b [ i ] \sum_{i=1}^{n}a[i]*b[i] ∑i=1na[i]∗b[i] 的最小值
思路: a a a 从小到大, b b b 从大到小,然后对应元素相乘结果最小
参考个人博客:贪心
相关文章:

Python贪心
贪心 贪心:把整体问题分解成多个步骤,在每个步骤都选取当前步骤的最优方案,直至所有步骤结束;每个步骤不会影响后续步骤核心性质:每次采用局部最优,最终结果就是全局最优如果题目满足上述核心性质…...

rk3568 内核态OOM内存泄漏kmemleak使用
1,配置,修改\kernel\arch\arm64\configs\rockchip_linux_defconfig,修改后查看.config. larkubuntu:~/Public/rk356x-linux/rk356x-linux/kernel$ cat .config | grep -i kmemleak CONFIG_HAVE_DEBUG_KMEMLEAKy CONFIG_DEBUG_KMEMLEAKy CONFI…...

ASP.NET Core - 日志记录系统(二)
ASP.NET Core - 日志记录系统(二) 2.4 日志提供程序2.4.1 内置日志提供程序2.4.2 源码解析 本篇接着上一篇 ASP.NET Core - 日志记录系统(一) 往下讲,所以目录不是从 1 开始的。 2.4 日志提供程序 2.4.1 内置日志提供程序 ASP.NET Core 包括…...

阿里云直播互动Web
官方文档:互动消息Web端集成方法_视频直播(LIVE)-阿里云帮助中心 以下是代码实现: <!-- 引入阿里云互动文件 --> <script src"https://g.alicdn.com/code/lib/jquery/3.7.1/jquery.min.js"></script> <script src&quo…...

解锁无证身份核验:开启便捷安全新征程
在当今快速发展的数字化时代,身份核验作为确保信息安全与交易诚信的基石,正经历着前所未有的变革。传统的身份核验方式,如携带身份证件进行现场验证,虽在一定程度上保障了安全,却也带来了诸多不便。随着科技的进步&…...

[DO374] Ansible 配置文件
[DO374] Ansible 配置文件 1. 配置文件位置2. 配置文件3. Ansible 配置4. Ansible的Ad-hoc5. Ansible 模块6. playbook段落7. 任务执行后续8. Ansible 变量8.1 ansible 变量的定义8.1.1 主机变量8.1.2 主机组变量 8.2 vars的循环 9. Ansible Collection10. Ansible-galaxy 安装…...

【杂谈】-50+个生成式人工智能面试问题(四)
7、生成式AI面试问题与微调相关 Q23. LLMs中的微调是什么? 答案:虽然预训练语言模型非常强大,但它们并不是任何特定任务的专家。它们可能对语言有惊人的理解能力,但仍需要一些LLMs微调过程,开发者通过这个过程提升它…...

RuoYi Cloud项目解读【四、项目配置与启动】
四、项目配置与启动 当上面环境全部准备好之后,接下来就是项目配置。需要将项目相关配置修改成当前相关环境。 1 后端配置 1.1 数据库 创建数据库ry-cloud并导入数据脚本ry_2024xxxx.sql(必须),quartz.sql(可选&…...

51c~Pytorch~合集5
我自己的原文哦~ https://blog.51cto.com/whaosoft/13059544 一、PyTorch DDP 正在郁闷呢 jetson nx 的torchvision安装~~ 自带就剩5g 想弄到ssd 项目中的 venv中又 cuda.h没有... 明明已经装好什么都对 算了说今天主题 啊对 还是搬运啊 学习之工具人而已 勿怪 Distrib…...

【芯片封测学习专栏 -- 什么是 Chiplet 技术】
请阅读【嵌入式开发学习必备专栏 Cache | MMU | AMBA BUS | CoreSight | Trace32 | CoreLink | ARM GCC | CSH】 文章目录 OverviewChiplet 背景UCIeChiplet 的挑战 Overview Chiplet 又称为小芯片。该技术通过将大型SoC划分为更小的芯片,使得每个部分都能采用不同…...
)
Java SpringBoot + Vue + Uniapp 集成JustAuth 最快实现多端三方登录!(QQ登录、微信登录、支付宝登录……)
注:本文基于 若依 集成just-auth实现第三方授权登录 修改完善,所有步骤仅代表本人如下环境亲测可用,其他环境需自辩或联系查看原因! 系统环境 运行系统:Windows10专业版、Linux Centos7.6 Java 版本:1.8.0_…...

支持向量回归(SVR:Support Vector Regression)用于A股数据分析、预测
简单说明 支持向量回归是一种用来做预测的数学方法,属于「机器学习」的一种。 它的目标是找到一条「最合适的线」,能够大致描述数据点的趋势,并允许数据点离这条线有一定的误差(不要求所有点都完全落在这条线上)。 可以把它想象成:找到一条「宽带」或「隧道」,大部分…...

ZYNQ初识10(zynq_7010)UART通信实验
基于bi站正点原子讲解视频: 系统框图(基于串口的数据回环)如下: 以下,是串口接收端的波形图,系统时钟和波特率时钟不同,为异步时钟,,需要先延时两拍,将时钟同…...

专题 - STM32
基础 基础知识 STM所有产品线(列举型号): STM产品的3内核架构(列举ARM芯片架构): STM32的3开发方式: STM32的5开发工具和套件: 若要在电脑上直接硬件级调试STM32设备,则…...

2 XDMA IP中断
三种中断 1. Legacy 定义:Legacy 中断是传统的中断处理方式,使用物理中断线(例如 IRQ)来传递中断信号。缺点: 中断线数量有限,通常为 16 条,限制了可连接设备的数量。中断处理可能会导致中断风…...
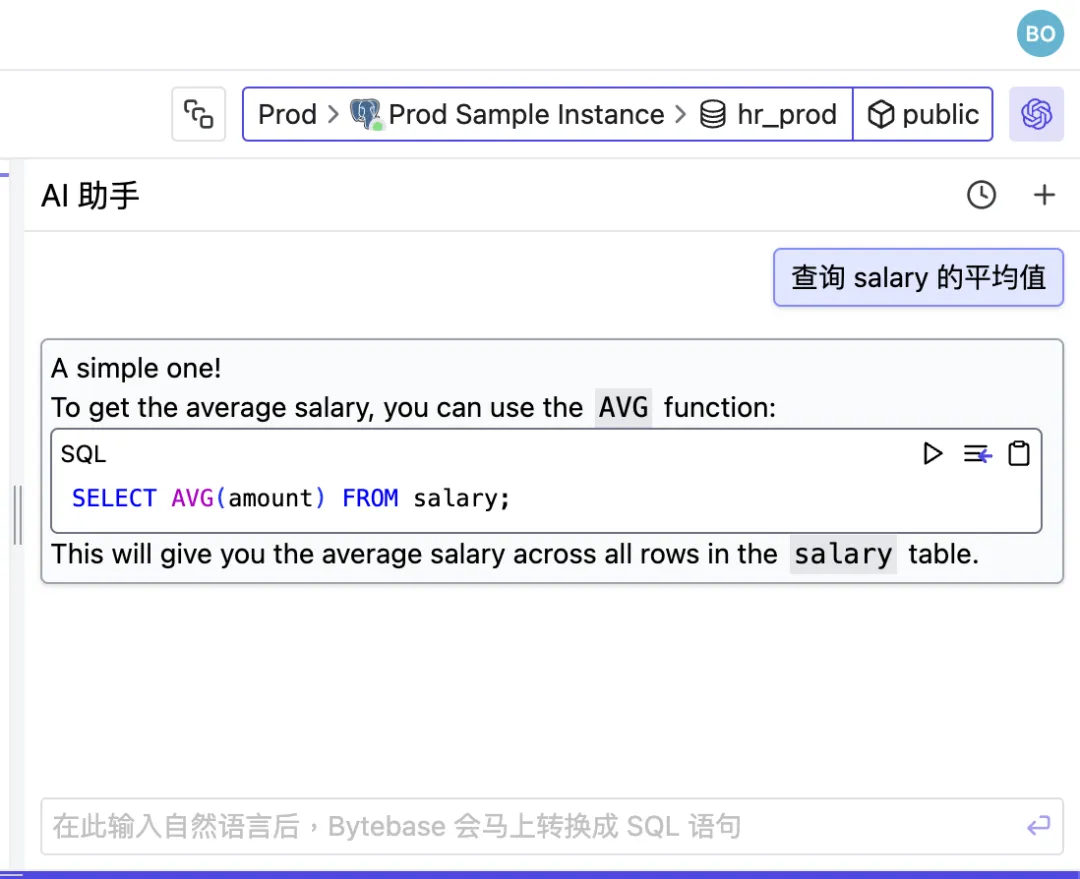
自然语言转 SQL:通过 One API 将 llama3 模型部署在 Bytebase SQL 编辑器
使用 Open AI 兼容的 API,可以在 Bytebase SQL 编辑器中使用自然语言查询数据库。 出于数据安全的考虑,私有部署大语言模型是一个较好的选择 – 本文选择功能强大的开源模型 llama3。 由于 OpenAI 默认阻止出站流量,为了简化网络配置&#…...

抖音矩阵是什么
抖音矩阵是指在同一品牌或个人IP下,通过创建多个不同定位的抖音账号(如主号、副号、子号等),形成一个有机的整体,以实现多维度、多层次的内容覆盖和用户互动。以下是关于抖音矩阵的详细介绍: 抖音矩阵的类…...

怎么抓取ios 移动app的https请求?
怎么抓取IOS应用程序里面的https? 这个涉及到2个问题 1.电脑怎么抓到IOS手机流量? 2.HTTPS怎么解密? 部分app可以使用代理抓包的方式,但是正式点的app用代理抓包是抓不到的,例如pin检测,证书双向校验等…...

pyqt鸟瞰
QApplication是Qt框架中的一个类,专门用于管理基于QWidget的图形用户界面(GUI)应用程序的控制流和主要设置。QApplication类继承自QGuiApplication,提供了许多与GUI相关的功能,如窗口系统集成、事件处理等。 QAppli…...
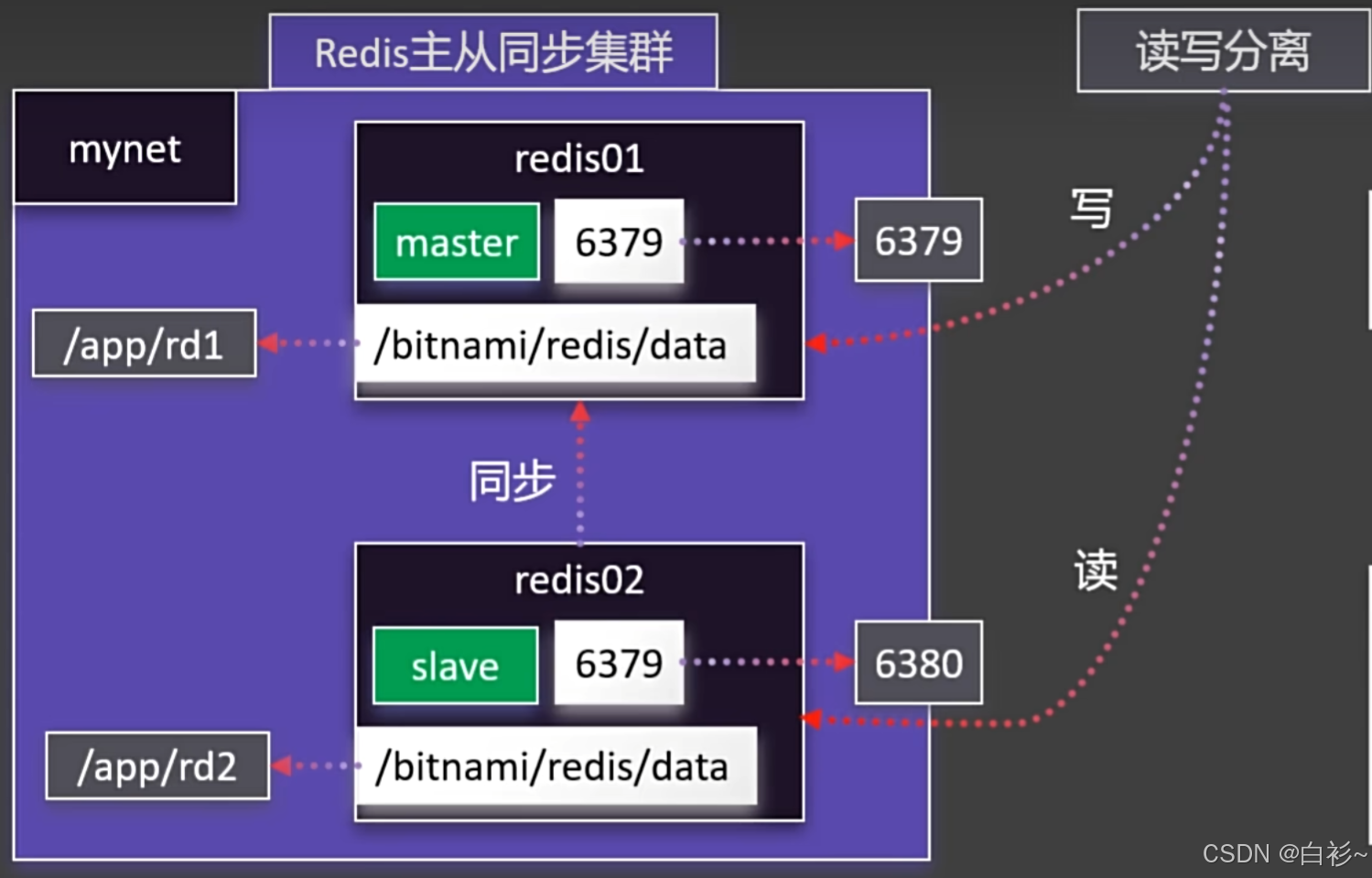
【Docker】入门教程
目录 一、Docker的安装 二、Docker的命令 Docker命令实验 1.下载镜像 2.启动容器 3.修改页面 4.保存镜像 5.分享社区 三、Docker存储 1.目录挂载 2.卷映射 四、Docker网络 1.容器间相互访问 2.Redis主从同步集群 3.启动MySQL 五、Docker Compose 1.命令式安装 …...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...
