Rust学习入门--【8】复合类型
复合类型(compound type)
可以将多个不同类型的值组合为一个类型。
Rust中提供了两种内置的复合数据类型:元组(tuple)和数组(array)。
元组类型
元组是一个具有 固定长度 的数据集合 —— 无法在声明结束后增加或减少其中的元素数量。
元素使用逗号分隔放入一对圆括号()中。元组每个位置的值都有一个类型,这些类型不需要是相同的。例如:
let tup: (i32, f64, u8) = (123, 6.5, 1);
// tup.0 等于 123
// tup.1 等于 6.5
// tup.2 等于 1
let (x, y, z) = tup;
// y 等于 6.5
由于一个元组被视作一个单独的复合元素,所以这里的变量tup被绑定到了整个元组上。为了从元组中获得单个的值,我们可以使用模式匹配来解构(destructuring)元组:
fn main() {let tup: (i32, f64, u8) = (123, 6.5, 1);let (x, y, z) = tup;println!("the value of y is: {}", y); // 输出 the value of y is: 6.6
}
除了解构,我们还可以通过索引并使用点号(.)来访问元组中的值:
fn main() {let tup: (i32, f64, u8) = (123, 6.5, 1);let x = tup.0;let y = tup.1;let z = tup.2;println!("x = {}, y = {}, z = {}", x, y, z); // 输出 x = 123, y = 6.5, z = 1
}
这段程序首先创建了一个元组tup,随后又通过索引访问元组的各个元素,并将它们的值绑定到新的变量上。元素的索引从 0 开始。
数组类型
Rust中的数组:
- 数组元素必须是相同的类型;
- 数组拥有固定的长度,一旦声明就不能随意更改大小。
在Rust中,将逗号分隔的值放置在一对**方括号[]**内来创建一个数组:
// arr 是一个长度为 5 的整型数组
let arr = [1, 2, 3, 4, 5];
定义数组是可以指定数组类型和大小,如:
//长度为 5 的 i32 数组
let arr: [i32; 5] = [1, 2, 3, 4, 5];
若声明的数组具有相同数值,可以按照如下形式定义:
// 等同于 let d = [3, 3, 3, 3, 3];
let arr = [3; 5];
对于一个数组 arr,可以通过索引访问其中的元素,比如 arr[2] 为数组 arr 中下标为 2 的元素。数组元素下标从 0 开始。例如下面的程序:
fn main() {let a = [1, 2, 3, 4, 5];println!("a[0] = {}, a[1] = {}", a[0], a[1]); // 输出 a[0] = 1, a[1] = 2
}
相关文章:

Rust学习入门--【8】复合类型
复合类型(compound type) 可以将多个不同类型的值组合为一个类型。 Rust中提供了两种内置的复合数据类型:元组(tuple)和数组(array)。 元组类型 元组是一个具有 固定长度 的数据集合 —— 无…...

【整理六】
1、props和state相同点和不同点?render方法在哪些情况下会执行? props是一个从外部传进组件的参数,由于React具有单向数据流的特性,所以他的主要作用是从父组件向子组件中传递数据,它是不可改变的,如果想要…...

Ubuntu20.04安装MySQL5.7与远程连接
一、安装MySQL5.7 1.更换镜像源 sudo cp /etc/apt/sources.list /etc/apt/sources.list.old #备份原来的文件 sudo vim /etc/apt/sources.list #修改sources.list文件配置文件内容如下所示: # 清华镜像源 deb https://mirrors.tuna.tsinghua.edu.cn/ubu…...
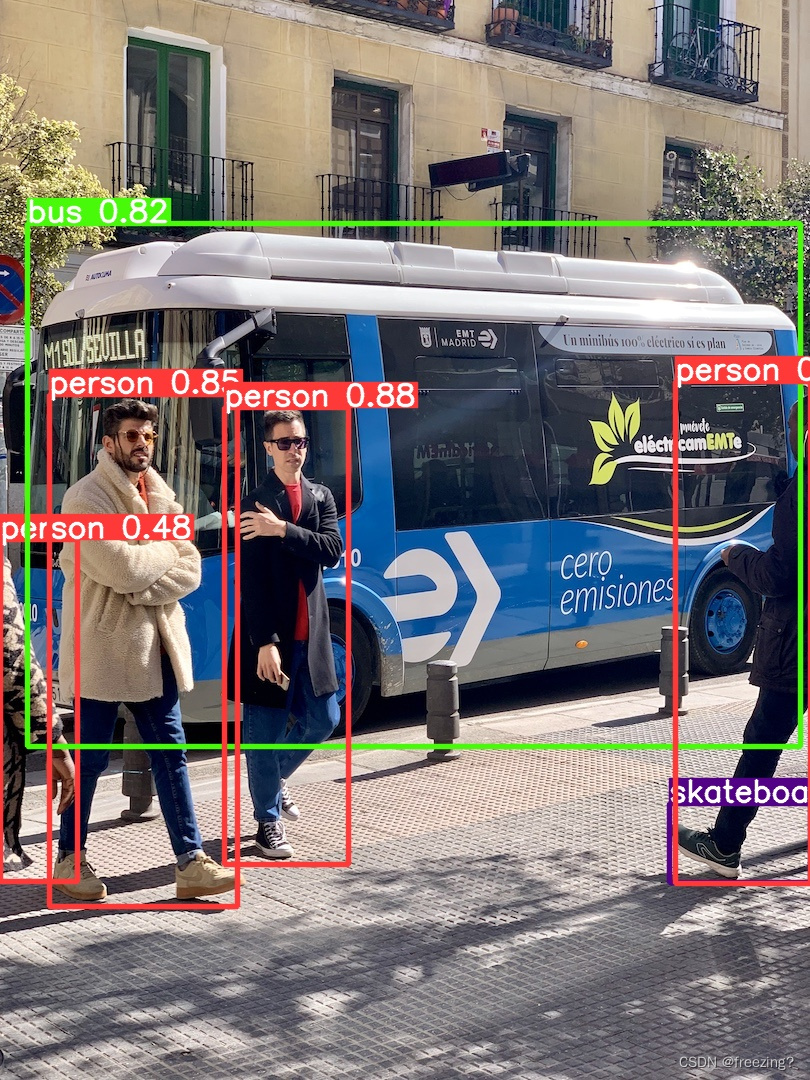
【yolov5】首次尝试目标检测利用prompt(完整操作流程)
1、打开prompt 2、切换到pytorch所在环境 conda activate freezing我的环境名是freezing,这里根据自己环境名去激活切换 3、进入到yolov5项目所在路径 激活完环境后立即执行指令当然是无效的,首先要进入到你的项目目录 首先看一下自己的项目在那个位…...

三大指标继续狂飙!重庆啤酒:不惧强弱分化加剧,深耕高端市场
十多年前,重庆啤酒因为9个跌停而被一片唱衰,资本市场经典的“关灯吃面”典故自此出现,被股民沿用至今。不过自2020年,重庆啤酒开始逆转走势,股价连续上涨。2021年重庆啤酒营收突破百亿大关,净赚11.66亿元&a…...

MySQL数据库14——更新和删除数据
SQL里面使用UPDATE更新数据,删除使用DELETE语句。 Mysql要修改一下设置,才能更新: 在左上角菜单栏里面选择偏好栏,取消下面这个红框的勾选 更新单个字段的数据 如果运行环境为MySQL 则使用以下语句进行备份。 CREATE TABLE stu…...

Java面试——MyBatis篇
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

C++的 new 和 delete
文章目录一、new 和 delete 的使用二、operator new 和 operator delete 函数三、new 和 delete 的实现原理四、申请空间和释放空间应配套使用五、定位 new 表达式六、malloc/free 和 new/delete 的区别C语言的动态内存管理函数(malloc、calloc、realloc、free) 虽然可以继续在…...

MySQL 事务原理
文章目录1、事务1.1、ACID 特性1.1.1、原子性undo log1.1.2、一致性1.1.3、* 隔离性1.1.4、持久性redo log1.2、事务控制语句2、隔离级别2.1、隔离级别的分类2.1.1、读未提交 RU2.1.2、读已提交 RC2.1.3、可重复读 RR2.1.4、串行化 SC2.2、并发事务读异常2.2.1、* 脏读2.2.2、*…...
软件测试面试自我介绍/项目介绍居然还有模板?我要是早点发现就好了
目录 1、自我介绍 2、项目介绍 2.1、最全电商项目介绍 2.2、电商项目介绍 2.3、在线教育项目介绍 2.4、互联网金融项目介绍 总结 1、自我介绍 以XXX简历来举例(参照下面的案例,编写你的自我介绍,框架就是:我是谁࿰…...

new RegExp的使用
1.RegExp是什么 当检索某个文本时,可以使用一种模式来描述要检索的内容。RegExp 就是这种模式 RegExp 对象用于存储检索模式。 var patt1new RegExp("e");当使用该 RegExp 对象在一个字符串中检索时,将寻找的是字符 “e” g :表…...

供应商管理软件如何选型 好用的供应商管理软件推荐
供应商管理是采购中的重要环节。对于很多企业来说,做好内部供应商管理就能在行业竞争中提升自身的效益与竞争能力,供应商已成为一种战略筹码。 但在企业进行供应商管理过程中,往往会遇到供应商信息数据收集不全、等级划分不合理、绩效评价机…...

Python3遍历文件夹提取关键字及其附近字符
要求: 1,遍历文件夹下所有的.xml文件 2,从.xml文件中提取关键字以及左右十个字符 3,输出到excel 一:遍历文件夹找到所有xml文件及其路径 for root, dirs, files in os.walk(self.inputFilePath):for file in files:…...

「1」线性代数(期末复习)
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀 第一章 行列式 行列式是一个数,是一个结果三阶行列式的计算:主对角线的乘…...

C++7:STL-模拟实现vector
目录 vector的成员变量 构造函数 reserve size() capacity() push_back 一些小BUG 赋值操作符重载 析构函数 【】操作符重载 resize pop_back Insert 迭代器失效 erase 二维数组问题 总结一下 vector,翻译软件会告诉你它的意思是向量,但其…...

笑死,面试官又问我SpringBoot自动配置原理
面试官:好久没见,甚是想念。今天来聊聊SpringBoot的自动配置吧? 候选者:嗯,SpringBoot的自动配置我觉得是SpringBoot很重要的“特性”了。众所周知,SpringBoot有着“约定大于配置”的理念,这一…...
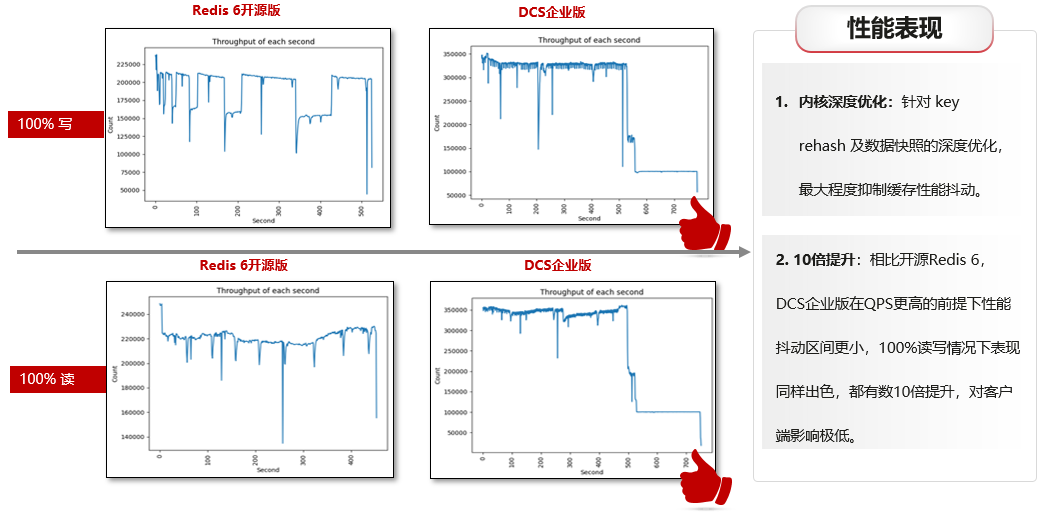
分布式缓存服务DCS-企业版性能更强,稳定性更高
背景介绍 近年来,随着各行业业务需求急速增加,数据量和并发访问量呈指数级增长,原来只能依附于关系型数据库的传统“缓存”逐渐难以支撑上层业务,开源Redis也面临着如“容量有限”、 “可靠性有限”、 “数据重复拷贝,…...

HTTP基本原理
目录URL简单定义格式HTTP和HTTPSHTTP的请求过程。请求响应响应体HTTP2.0总结URL 简单定义 通过一个链接,使我们可以找到网络上的某个资源,这个链接就是URL。 格式 URL并不是随便写的,而是有固定的格式。基本的组成格式如下。 schme://[us…...
最新版本详细保姆级安装教程)
【云原生】Kubernetes(k8s)最新版本详细保姆级安装教程
前言 Kubernetes简称k8s,是一个开源的,用于管理云平台中多个主机上的容器化的应用,k8s目标是让部署容器化的应用简单并且高效,k8s提供了应用部署,规划,更新,维护的一种机制。 本文是总结了在安…...
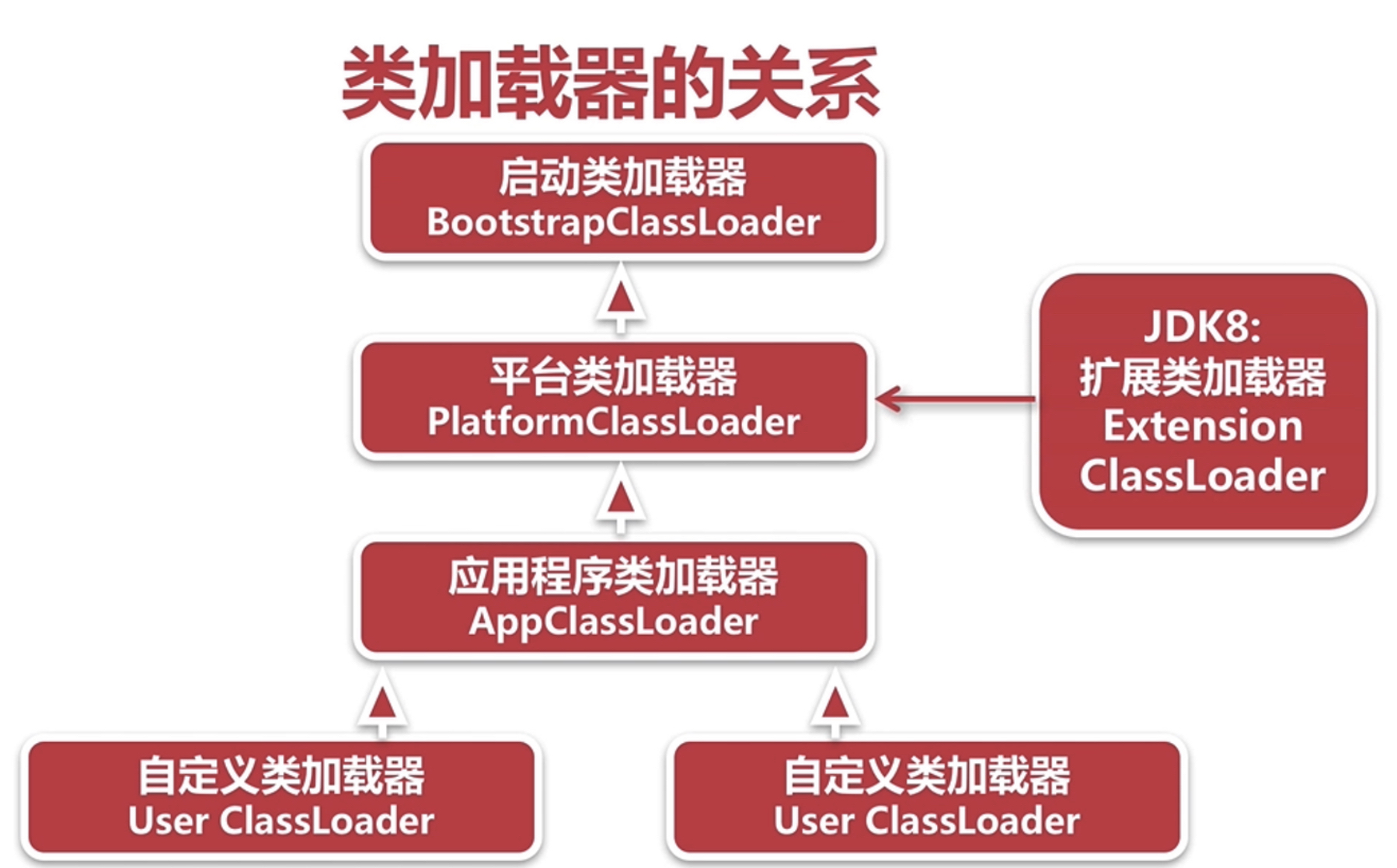
JVM - 类加载,连接和初始化
目录 类加载和类加载器 概述 类加载要完成的功能 加载类的方式 类加载器 类加载器的关系 类加载器说明 双亲委派模型 工作过程如下: 双亲委派模型说明: 破坏双亲委派模型: 类连接和初始化 类连接主要验证的内容 类连接中的解析…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
