数据结构与算法:动态规划dp:理论基础和相关力扣题(509.斐波那契数列、70.爬楼梯)
1.0.理论基础
动态规划主要解决的问题种类有:
- 背包问题
- 打家劫舍
- 股票问题
- 子序列问题
解决步骤:
- dp数组及其下标的意义
- 递推公式
- dp数组初始化
- 遍历顺序
- 打印dp数组
2.0.相关力扣题
509.斐波那契数列
class Solution:def fib(self, n: int) -> int:if n==0:return 0if n==1:return 1dp = [0]*35dp[1] = 1for i in range(2,31):dp[i] = dp[i-1]+dp[i-2]return dp[n]
效率:0ms,击败100.00%
状态压缩
再优化一下,因为每个斐波那契数只和它相邻的两个数有关,所以我们其实不需要存储三十多个长度,只需要保留2个数的信息即可。也就是状态压缩。
class Solution:def fib(self, n: int) -> int:if n==0:return 0if n==1:return 1dp = [0]*2dp[1]=1sum = 0for i in range(2,n):sum = dp[0]+dp[1]dp[0] = dp[1]dp[1] = sumreturn dp[0]+dp[1]
70.爬楼梯
跟509.斐波那契数列很像
class Solution:def climbStairs(self, n: int) -> int:if n==1:return 1if n==2:return 2dp = [0] * 50dp[1] = 1dp[2] = 2for i in range(3,n+1):dp[i] = dp[i-1]+dp[i-2]print(dp)return dp[n]效率:0ms,击败100.00%
状态压缩
class Solution:def climbStairs(self, n: int) -> int:if n==1:return 1if n==2:return 2dp = [0] * 4dp[1] = 1dp[2] = 2sum = 0for i in range(3,n):sum = dp[1]+dp[2]dp[1] = dp[2]dp[2] = sumreturn dp[1]+dp[2]
756.使用最小代价爬楼梯
需要注意的是,这里的dp[i]代表着爬到台阶为i时所需的最小代价。
class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:n = len(cost)if n == 2:return min(cost[0],cost[1])dp = [0]*1005dp[0] = 0dp[1] = 0for i in range(2,n+1):dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])return dp[n]
效率:2ms,击败83.69%
相关文章:
)
数据结构与算法:动态规划dp:理论基础和相关力扣题(509.斐波那契数列、70.爬楼梯)
1.0.理论基础 动态规划主要解决的问题种类有: 背包问题打家劫舍股票问题子序列问题 解决步骤: dp数组及其下标的意义递推公式dp数组初始化遍历顺序打印dp数组 2.0.相关力扣题 509.斐波那契数列 class Solution:def fib(self, n: int) -> int:i…...

某政务行业基于 SeaTunnel 探索数据集成平台的架构实践
分享嘉宾:某政务公司大数据技术经理 孟小鹏 编辑整理:白鲸开源 曾辉 导读:本篇文章将从数据集成的基础概念入手,解析数据割裂给企业带来的挑战,阐述数据集成的重要性,并对常见的集成场景与工具进行阐述&…...

word-break控制的几种容器换行行为详解
word-break 属性在控制换行行为时需要根据语言判断,对于中文 一个字符就是一个单词,字符换行不影响阅读理解,而对于英文来说,多个连续的字符才会是一个单词,例如中文的 早 英文为 morning。 morning7个字符才算一个单词…...

【0x0084】HCI_Set_Min_Encryption_Key_Size命令详解
目录 一、命令概述 二、命令格式及参数 2.1 HCI_Set_Min_Encryption_Key_Size命令格式 2.2. Min_Encryption_Key_Size 三、生成事件及参数 3.1. HCI_Command_Complete 事件 3.2. Status 四、命令的执行流程 4.1. 主机端准备阶段 4.2. 命令发送阶段 4.3. 控制器接收和…...

关于2025年智能化招聘管理系统平台发展趋势
2025年,招聘管理领域正站在变革的十字路口,全新的技术浪潮与不断变化的职场生态相互碰撞,促使招聘管理系统成为重塑企业人才战略的关键力量。智能化招聘管理系统平台在这一背景下迅速崛起,其发展趋势不仅影响企业的招聘效率与质量…...
Docker部署Spring Boot + Vue项目
目录 前提条件 概述 下载代码 打开代码 Docker创建网络 MySQL容器准备 MySQL数据库配置 启动MySQL容器 测试连接MySQL 初始化MySQL数据 Redis容器准备 修改Redis配置 启动redis容器 部署后端 后端代码打包 上传jar包到Linux 创建Dockerfile 构建镜像 运行后…...

开发规范
开发规范 企业项目开发有2种开发模式:前后台混合开发和前后台分离开发。 前后台混合开发 顾名思义就是前台后台代码混在一起开发,如下图所示: 这种开发模式有如下缺点: 沟通成本高:后台人员发现前端有问题…...
九 RK3568 android11 MPU6500
一 MPU6500 内核驱动 1.1 查询设备连接地址 查看原理图, MPU6500 I2C 连接在 I2C4 上, 且中断没有使用 i2c 探测设备地址为 0x68 1.2 驱动源码 drivers/input/sensors/gyro/mpu6500_gyro.c drivers/input/sensors/accel/mpu6500_acc.c 默认 .config 配置编译了 mpu6550 …...
openplant实时数据库(二次开发)
资源地址 我的网盘〉软件>数据库>openplant>openplant实时数据库(二次开发)...
C语言:-三子棋游戏代码:分支-循环-数组-函数集合
思路分析: 1、写菜单 2、菜单之后进入游戏的操作 3、写函数 实现游戏 3.1、初始化棋盘函数,使数组元素都为空格 3.2、打印棋盘 棋盘的大概样子 3.3、玩家出棋 3.3.1、限制玩家要下的坐标位置 3.3.2、判断玩家要下的位置是否由棋子 3.4、电脑出棋 3.4.1、…...

“AI智慧化服务系统:未来生活的智能管家
在当今快速发展的科技时代,人工智能(AI)正以前所未有的速度改变着我们的生活。AI智慧化服务系统作为这一变革的前沿技术,正在逐渐成为我们未来生活的智能管家。它们不仅提高了服务效率,还为我们带来了更加个性化和便捷…...

python管理工具:conda部署+使用
python管理工具:conda部署使用 一、安装部署 1、 下载 - 官网下载: https://repo.anaconda.com/archive/index.html - wget方式: wget -c https://repo.anaconda.com/archive/Anaconda3-2023.03-1-Linux-x86_64.sh2、 安装 在conda文件的…...

minio https配置
minio启动时候指定数据目录,配置文件,密钥文件目录,环境文件 1.创建minio用户,专门用于服务启动的 groupadd -r minio-user useradd -M -r -g minio-user minio-user 2.在当前用户目录下创建minio目录,存储minio相关文件 mkdir minio 在mini…...
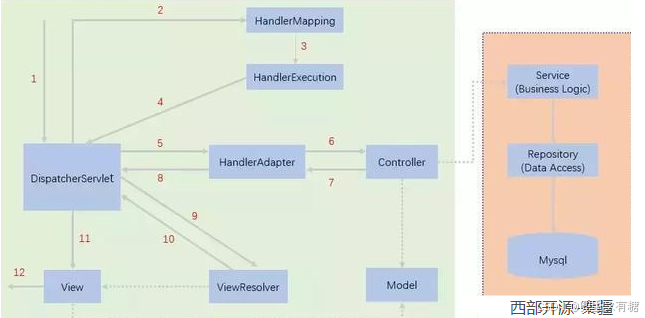
SpringMVC——原理简介
狂神SSM笔记 DispatcherServlet——SpringMVC 的核心 SpringMVC 围绕DispatcherServlet设计。 DispatcherServlet的作用是将请求分发到不同的处理器(即不同的Servlet)。根据请求的url,分配到对应的Servlet接口。 当发起请求时被前置的控制…...
Ubuntu18.04 解决 libc.so.6: version `GLIBC_2.28‘ not found
Glibc(GNU C Library)是 GNU 系统及其衍生系统如 Linux 操作系统中实现 C 语言标准库的核心组件。升级 Glibc 是一个非常谨慎的操作,因为它与系统的许多关键功能和服务密切相关。Ubuntu 18.04 默认安装的 Glibc 版本为 2.27,但某些…...
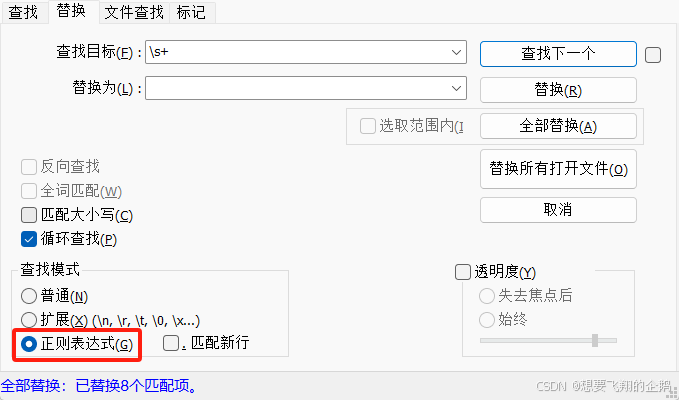
Notepad++移除所有空格
1.打开Notepad。 2.打开你想要编辑的文件。 3.按下 Ctrl H 打开查找和替换对话框,并选择 “正则表达式”。 4.在 “查找目标” 框中输入 \s。 5.在 “替换为” 框中留空,不填写任何内容。 6.点击 “全部替换” 按钮。...

Android BottomNavigationView不加icon使text垂直居中,完美解决。
这个问题网上千篇一律的设置iconsize为0,labale固定什么的,都没有效果。我的这个基本上所有人用都会有效果。 问题解决之前的效果:垂直方向,文本不居中,看着很难受 问题解决之后:舒服多了 其实很简单&…...

如何使用 `forEach` 遍历数组?
数组遍历相关问题:如何使用 forEach 遍历数组? 在 JavaScript 中,遍历数组是一个常见且必要的操作。数组提供了多种方法来进行遍历,其中 forEach 是一种非常方便且常用的方法。它可以轻松地对数组中的每个元素执行回调函数。理解…...

Go语言之路————条件控制:if、for、switch
Go语言之路————if、for、switch 前言ifforswitchgoto和label 前言 我是一名多年Java开发人员,因为工作需要现在要学习go语言,Go语言之路是一个系列,记录着我从0开始接触Go,到后面能正常完成工作上的业务开发的过程࿰…...
OpenAI推出首个AI Agent!日常事项自动化处理!
2025 年1月15日,OpenAI 正式宣布推出一项名为Tasks的测试版功能 。 该功能可以根据你的需求内容和时间实现自动化处理。比方说,你可以设置每天早晨 7 点获取天气预报,或定时提醒遛狗等日常事项。 看到这里,有没有一种熟悉的感觉&a…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
