npm命令与yarn命令的区别
npm与Yarn的区别详解
在软件开发中,npm和Yarn都是流行的包管理工具,它们各自拥有独特的特性和优势。以下是它们的主要区别:
1. 安装速度
- npm:安装速度相对较慢,尤其是在依赖项较多的情况下。
- Yarn:采用并行下载和缓存机制,安装速度较快,尤其在网络条件良好的情况下。
2. 磁盘空间占用
- npm:默认将依赖项复制到项目的node_modules目录,可能导致重复占用磁盘空间。
- Yarn:通过缓存机制减少磁盘空间占用,特别是在离线模式下。
3. 并发安装
- npm:不支持并发安装,会逐个安装依赖项。
- Yarn:支持并发安装,利用并行下载提高安装速度。
4. 稳定性
- npm:稳定且成熟,广泛使用,由node.js社区维护。
- Yarn:由Facebook维护,稳定性较高,支持更多现代特性。
5. 命令行界面
- npm:命令行界面随着版本更新不断改进,但在某些方面可能不如Yarn友好。
- Yarn:提供更加友好和一致的命令行输出,特别是在处理错误和依赖冲突时。
6. 社区和扩展
- npm:拥有庞大的社区和生态系统,是全球最大的JavaScript包仓库。
- Yarn:由Facebook开发,得到许多大型项目和公司的支持,支持工作区功能,便于管理monorepo项目。
综合推荐
选择哪种包管理工具取决于项目的具体需求和个人偏好。如果你需要一个稳定且成熟的解决方案,npm可能是更好的选择。相反,如果你重视安装速度和磁盘空间管理,Yarn可能更适合你。无论选择哪种工具,都建议在单一项目中保持一致,以避免潜在的兼容性问题。
相关文章:

npm命令与yarn命令的区别
npm与Yarn的区别详解 在软件开发中,npm和Yarn都是流行的包管理工具,它们各自拥有独特的特性和优势。以下是它们的主要区别: 1. 安装速度 npm:安装速度相对较慢,尤其是在依赖项较多的情况下。Yarn:采用并…...

python如何导出数据到excel文件
python导出数据到excel文件的方法: 1、调用Workbook()对象中的add_sheet()方法 wb xlwt.Workbook() ws wb.add_sheet(A Test Sheet) 2、通过add_sheet()方法中的write()函数将数据写入到excel中,然后使用save()函数保存excel文件 ws.write(0, 0, 1234…...
:单行函数(字符串、数学、日期时间、条件判断、信息、加密、进制转换函数)讲解)
MYSQL学习笔记(五):单行函数(字符串、数学、日期时间、条件判断、信息、加密、进制转换函数)讲解
前言: 学习和使用数据库可以说是程序员必须具备能力,这里将更新关于MYSQL的使用讲解,大概应该会更新30篇,涵盖入门、进阶、高级(一些原理分析);这一篇是讲解单行函数,当然mysql函数很多哈,只有多用才能记得…...

Grafana系列之Dashboard:新增仪表板、新增变量、过滤变量、变量查询、导入仪表板、变量联动、Grafana Alert
概述 关于Prometheus和Grafana的安装,略过。 写在前面 Dashboard:仪表板,可包含多个PanelPanel:面板,Dashboard中的组件 如有写得不对的地方,烦请指出。 新增仪表板 点击右上角的 选择New dashboard…...
基于Misty1算法的加密软件的实现-毕业设计)
(java版本)基于Misty1算法的加密软件的实现-毕业设计
一、基于Misty1算法的加密软件(Java)的实现 随着计算机网络及通信技术的飞速发展,信息安全成了信息社会急需解决的最重要的问题之一,密码技术是保证信息安全的核心技术。本文用JAVA语言开发了一个基于Misty1算法的加密软件&#x…...

Spring注解篇:@RestController详解
全文目录: 开篇语前言摘要概述源码解析使用案例分享代码分析使用场景优缺点分析测试用例 应用场景案例优缺点分析核心类方法介绍测试用例测试用例分析使用场景优缺点分析测试用例 小结总结文末 开篇语 哈喽,各位小伙伴们,你们好呀,…...

C++:将字符数组rkpryyrag,每个字母转换为其前面第13个字母后输出,如果超过a则从z再继续接着数。例如:b前面第1个字母是a。a前面第3个字母是x。
代码如下: #include <iostream> #include <string> using namespace std;int main(){string str "rkpryyrag";for (int i 0; i < str.length(); i){if (str[i] > a && str[i] < z){if (str[i] - a < 13){cout <<…...

《探秘鸿蒙Next:人工智能助力元宇宙高效渲染新征程》
在元宇宙的宏大愿景中,高效的渲染技术是构建沉浸式虚拟世界的关键。鸿蒙Next凭借与人工智能的深度融合,为元宇宙的渲染带来了全新的解决方案和无限可能。 智能场景分析与优化 人工智能能够对元宇宙场景进行智能分析。鸿蒙Next可以利用AI技术对场景中的…...

微前端qiankun的部署
微前端qiankun的部署 本地开发主应用配置启动端口子应用配置启动端口测试环境部署:场景 1:主应用和微应用部署到同一个服务器(同一个 IP 和端口)微应用都放在在一个特殊名称(不会和微应用重名)的文件夹下主应用配置子应用配置配置nginx本地开发 主应用配置启动端口 打开…...

HTML表格-掌握表格标签与属性
HTML表格是网页设计中用于展示数据的强大工具,它通过一系列标签和属性来控制表格的布局和样式。 一、HTML表格的基本结构 HTML表格由<table>标签定义,内部包含多个行(<tr>)、单元格(<td>或<th&…...

PID控制的优势与LabVIEW应用
PID控制(比例-积分-微分控制)已在工业控制领域得到广泛应用,尤其在实时控制和自动化系统中,其核心优点是简单、稳定且高效。尽管许多现代控制方法(如自适应控制、模型预测控制等)逐渐崭露头角,P…...

全球化趋势与中资企业出海背景
1. 全球化趋势与中资企业出海背景 1.1 全球经济格局变化 全球经济格局正经历深刻变革,新兴经济体崛起,全球产业链重塑,中资企业出海面临新机遇与挑战。据世界银行数据,新兴市场和发展中经济体在全球 GDP 中占比已超 40%ÿ…...

Oracle之RMAN备份异机恢复(单机到单机)
Oracle之RMAN备份异机恢复(单机到单机) 一、环境说明二、正式库进行RMAN备份三、将正式库备份与参数文件拷贝到测试库四、测试库异机恢复五、验证数据 一、环境说明 系统版本主机名DB版本DB名实例名Public-IP正式库Redhat9.5lemonEnterprise 19.25lemon…...

Servlet快速入门
Servlet 由于目前主流使用SpringBoot进行开发Servlet可以说是时代的眼泪,这篇文章主要介绍我基于SpringBoot对应Servlet的浅薄认知,有利于更好的理解前端界面和java服务器的数据交换过程 快速入门 我比较推荐这篇文章来对Servlet有一个大概的了解 都2…...

深入解析 Linux 内核中的 InfiniBand 驱动接口:ib_verbs.h
InfiniBand(IB)是一种高性能、低延迟的网络互连技术,广泛应用于高性能计算(HPC)、数据中心和云计算等领域。Linux 内核通过 InfiniBand 子系统提供了对 IB 设备的支持,而 ib_verbs.h 是 InfiniBand 驱动开发中的核心头文件之一。它定义了 IB 核心框架与用户空间接口(ver…...

vulnhub靶场【kioptrix-1靶机】
前言 靶机:kioptrix-1,IP地址为192.168.1.104 攻击:kali,IP地址为192.168.1.16 都采用虚拟机,网卡为桥接模式 文章中涉及的靶机,来源于vulnhub官网,想要下载,可自行访问官网下载&…...

Linux 6.14 内核的主要特性
原文参考:https://www.kernel.org/ Linux 6.14 内核是 Linux 内核的一个重要版本,预计于 2025 年 3 月发布。该版本引入了多项新特性和改进,涵盖了硬件支持、性能优化、安全性增强以及新技术的整合。 1. Rust 语言驱动的正式支持 Linux 6.1…...

【Linux】深刻理解动静态库
1.什么是库 库是写好的现有的,成熟的,可以复⽤的代码。现实中每个程序都要依赖很多基础的底层库,不可能每个⼈的代码都从零开始,因此库的存在意义⾮同寻常。本质上来说库是⼀种可执⾏代码的⼆进制形式,可以被操作系统载…...
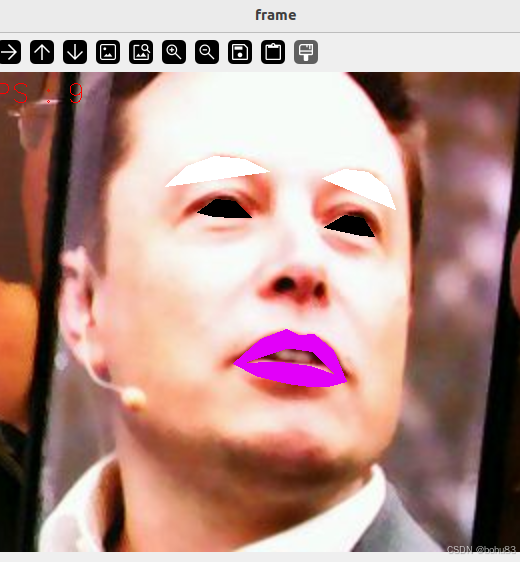
亚博microros小车-原生ubuntu支持系列:8-脸部检测与人脸特效
前面的都是使用了mediapipe框架。后面的这两节采用了opencv\dlib的框架。 一 脸部检测 核心:opencv detectMultiScale函数 detectMultiScale(image, scaleFactor, minNeighbors, flags, minSize, maxSize) image--待检测图片,一般为灰度图像加快检测…...

代码随想录算法训练营day32
代码随想录算法训练营 —day32 文章目录 代码随想录算法训练营前言一、动态规划理论基础二、509. 斐波那契数动态规划动态规划优化空间版递归法 三、70. 爬楼梯动态规划动态规划空间优化 746. 使用最小花费爬楼梯动态规划空间优化 总结 前言 今天是算法营的第32天,…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...
