多层 RNN原理以及实现
数学原理
多层 RNN 的核心思想是堆叠多个 RNN 层,每一层的输出作为下一层的输入,从而逐层提取更高层次的抽象特征。
1. 单层 RNN 的数学表示
首先,单层 RNN 的计算过程如下。对于一个时间步 t t t,单层 RNN 的隐藏状态 h t h_t ht 和输出 y t y_t yt 可以表示为:
h t = activation ( W i h x t + b i h + W h h h t − 1 + b h h ) h_t = \text{activation}(W_{ih} x_t + b_{ih} + W_{hh} h_{t-1} + b_{hh}) ht=activation(Wihxt+bih+Whhht−1+bhh)
y t = W h o h t + b h o y_t = W_{ho} h_t + b_{ho} yt=Whoht+bho
其中:
- x t x_t xt 是时间步 t t t 的输入。
- h t h_t ht 是时间步 t t t 的隐藏状态。
- h t − 1 h_{t-1} ht−1 是时间步 t − 1 t-1 t−1 的隐藏状态。
- W i h W_{ih} Wih、 W h h W_{hh} Whh、 W h o W_{ho} Who 是权重矩阵。
- b i h b_{ih} bih、 b h h b_{hh} bhh、 b h o b_{ho} bho 是偏置项。
- activation \text{activation} activation 是激活函数(如 tanh \tanh tanh 或 ReLU \text{ReLU} ReLU)。
2. 多层 RNN 的数学表示
假设我们有一个 L L L 层的 RNN,每一层的隐藏状态为 h t ( l ) h_t^{(l)} ht(l),其中 l l l 表示第 l l l 层, t t t 表示时间步。多层 RNN 的计算过程如下:
(1) 第一层( l = 1 l = 1 l=1)
第一层的输入是原始输入序列 x t x_t xt,隐藏状态 h t ( 1 ) h_t^{(1)} ht(1) 的计算公式为:
h t ( 1 ) = activation ( W i h ( 1 ) x t + b i h ( 1 ) + W h h ( 1 ) h t − 1 ( 1 ) + b h h ( 1 ) ) h_t^{(1)} = \text{activation}(W_{ih}^{(1)} x_t + b_{ih}^{(1)} + W_{hh}^{(1)} h_{t-1}^{(1)} + b_{hh}^{(1)}) ht(1)=activation(Wih(1)xt+bih(1)+Whh(1)ht−1(1)+bhh(1))
其中:
- W i h ( 1 ) W_{ih}^{(1)} Wih(1)、 W h h ( 1 ) W_{hh}^{(1)} Whh(1) 是第一层的权重矩阵。
- b i h ( 1 ) b_{ih}^{(1)} bih(1)、 b h h ( 1 ) b_{hh}^{(1)} bhh(1) 是第一层的偏置项。
(2) 第 l l l 层( l > 1 l > 1 l>1)
第 l l l 层的输入是第 l − 1 l-1 l−1 层的输出 h t ( l − 1 ) h_t^{(l-1)} ht(l−1),隐藏状态 h t ( l ) h_t^{(l)} ht(l) 的计算公式为:
h t ( l ) = activation ( W i h ( l ) h t ( l − 1 ) + b i h ( l ) + W h h ( l ) h t − 1 ( l ) + b h h ( l ) ) h_t^{(l)} = \text{activation}(W_{ih}^{(l)} h_t^{(l-1)} + b_{ih}^{(l)} + W_{hh}^{(l)} h_{t-1}^{(l)} + b_{hh}^{(l)}) ht(l)=activation(Wih(l)ht(l−1)+bih(l)+Whh(l)ht−1(l)+bhh(l))
其中:
- W i h ( l ) W_{ih}^{(l)} Wih(l)、 W h h ( l ) W_{hh}^{(l)} Whh(l) 是第 l l l 层的权重矩阵。
- b i h ( l ) b_{ih}^{(l)} bih(l)、 b h h ( l ) b_{hh}^{(l)} bhh(l) 是第 l l l 层的偏置项。
(3) 输出层
最后一层(第 L L L 层)的输出 h t ( L ) h_t^{(L)} ht(L) 作为整个网络的输出 y t y_t yt:
y t = W h o h t ( L ) + b h o y_t = W_{ho} h_t^{(L)} + b_{ho} yt=Whoht(L)+bho
其中:
- W h o W_{ho} Who、 b h o b_{ho} bho 是输出层的权重矩阵和偏置项。
3. 多层 RNN 的数据流向
以下是一个 L L L 层 RNN 的数据流向的数学描述:
(1) 输入序列
输入序列为 x 1 , x 2 , … , x T x_1, x_2, \dots, x_T x1,x2,…,xT,其中 T T T 是序列长度。
(2) 初始化隐藏状态
每一层的初始隐藏状态 h 0 ( l ) h_0^{(l)} h0(l) 通常初始化为零或随机值:
h 0 ( l ) = 0 或 h 0 ( l ) ∼ N ( 0 , σ 2 ) h_0^{(l)} = \mathbf{0} \quad \text{或} \quad h_0^{(l)} \sim \mathcal{N}(0, \sigma^2) h0(l)=0或h0(l)∼N(0,σ2)
(3) 时间步 t t t 的计算
对于每个时间步 t t t,从第一层到第 L L L 层依次计算隐藏状态:
-
第一层:
h t ( 1 ) = activation ( W i h ( 1 ) x t + b i h ( 1 ) + W h h ( 1 ) h t − 1 ( 1 ) + b h h ( 1 ) ) h_t^{(1)} = \text{activation}(W_{ih}^{(1)} x_t + b_{ih}^{(1)} + W_{hh}^{(1)} h_{t-1}^{(1)} + b_{hh}^{(1)}) ht(1)=activation(Wih(1)xt+bih(1)+Whh(1)ht−1(1)+bhh(1)) -
第 l l l 层( l > 1 l > 1 l>1):
h t ( l ) = activation ( W i h ( l ) h t ( l − 1 ) + b i h ( l ) + W h h ( l ) h t − 1 ( l ) + b h h ( l ) ) h_t^{(l)} = \text{activation}(W_{ih}^{(l)} h_t^{(l-1)} + b_{ih}^{(l)} + W_{hh}^{(l)} h_{t-1}^{(l)} + b_{hh}^{(l)}) ht(l)=activation(Wih(l)ht(l−1)+bih(l)+Whh(l)ht−1(l)+bhh(l)) -
输出:
y t = W h o h t ( L ) + b h o y_t = W_{ho} h_t^{(L)} + b_{ho} yt=Whoht(L)+bho
(4) 序列输出
最终,整个序列的输出为 y 1 , y 2 , … , y T y_1, y_2, \dots, y_T y1,y2,…,yT。
4. 多层 RNN 的特点
(1) 逐层抽象
- 每一层 RNN 可以看作是对输入序列的不同层次的抽象。
- 较低层捕捉局部和细节信息,较高层捕捉全局和语义信息。
(2) 参数共享
- 每一层的参数(权重矩阵和偏置项)在时间步之间共享。
- 不同层的参数是独立的。
(3) 梯度传播
- 在反向传播时,梯度会通过时间步和层数传播。
- 由于梯度消失或爆炸问题,训练深层 RNN 可能会比较困难。
可视化原理
下面是一个可视化的结构显示图:其中每一层神经元都要有两个方向的输出,一个是向本时间步的下一层传送,另一个是向下一个时间步的本层传送。而且,每一个神经元都有两个权重矩阵。注意:下方右图仅仅是逻辑上展开的数据流,其中不同世间步上的同一层,用的是同一个权重矩阵。

代码实现
1. 示例任务
假设有一个简单的任务:
- 处理一个长度为 4 的序列
- 批次大小为 2
- 每个时间步的输入特征维度为 3
- 希望使用一个 2 层的单向 RNN
- 隐藏状态维度为 5。
2. 输入数据
输入句子
- 句子 1: “I love PyTorch”
- 句子 2: “RNN is fun”
输入数据的形状
- 序列长度 (
seq_len): 4(假设每个单词是一个时间步) - 批次大小 (
batch_size): 2 - 输入特征维度 (
input_size): 3(假设每个单词用一个 3 维向量表示)
具体输入数据
import torch# 输入数据形状: (seq_len, batch_size, input_size)
input_data = torch.tensor([# 时间步 1[[0.1, 0.2, 0.3], # 句子 1 的第一个单词[0.4, 0.5, 0.6]], # 句子 2 的第一个单词# 时间步 2[[0.7, 0.8, 0.9], # 句子 1 的第二个单词[1.0, 1.1, 1.2]], # 句子 2 的第二个单词# 时间步 3[[1.3, 1.4, 1.5], # 句子 1 的第三个单词[1.6, 1.7, 1.8]], # 句子 2 的第三个单词# 时间步 4[[1.9, 2.0, 2.1], # 句子 1 的第四个单词[2.2, 2.3, 2.4]] # 句子 2 的第四个单词
])
print("Input shape:", input_data.shape) # 输出: torch.Size([4, 2, 3])
3. 初始隐藏状态
初始隐藏状态的形状
- RNN 层数 (
num_layers): 2 - 方向数 (
num_directions): 1(单向 RNN) - 批次大小 (
batch_size): 2 - 隐藏状态维度 (
hidden_size): 5
具体初始隐藏状态
# 初始隐藏状态形状: (num_layers * num_directions, batch_size, hidden_size)
h0 = torch.zeros(2, 2, 5) # 2层RNN,批次大小为2,隐藏状态维度为5
print("h0 shape:", h0.shape) # 输出: torch.Size([2, 2, 5])
4. 定义 RNN 模型
import torch.nn as nn# 定义 RNN
rnn = nn.RNN(input_size=3, # 输入特征维度hidden_size=5, # 隐藏状态维度num_layers=2, # RNN 层数batch_first=False # 输入形状为 (seq_len, batch_size, input_size)
)
5. 前向传播
计算输出
# 前向传播
output, hn = rnn(input_data, h0)print("Output shape:", output.shape) # 输出: torch.Size([4, 2, 5])
print("hn shape:", hn.shape) # 输出: torch.Size([2, 2, 5])
输出解析
-
output:- 形状为
(seq_len, batch_size, hidden_size),即(4, 2, 5)。 - 包含了每个时间步的隐藏状态。
- 例如,
output[0]是第一个时间步的隐藏状态,output[-1]是最后一个时间步的隐藏状态。
- 形状为
-
hn:- 形状为
(num_layers, batch_size, hidden_size),即(2, 2, 5)。 - 包含了最后一个时间步的隐藏状态。
- 例如,
hn[0]是第一层的最终隐藏状态,hn[1]是第二层的最终隐藏状态。
- 形状为
6. 具体输出值
output 的值
print("Output (所有时间步的隐藏状态):")
print(output)
输出示例:
tensor([[[ 0.1234, 0.5678, 0.9101, 0.1121, 0.3141],[ 0.4151, 0.6171, 0.8191, 0.0212, 0.2232]],[[ 0.4252, 0.6272, 0.8292, 0.0313, 0.2333],[ 0.4353, 0.6373, 0.8393, 0.0414, 0.2434]],[[ 0.4454, 0.6474, 0.8494, 0.0515, 0.2535],[ 0.4555, 0.6575, 0.8595, 0.0616, 0.2636]],[[ 0.4656, 0.6676, 0.8696, 0.0717, 0.2737],[ 0.4757, 0.6777, 0.8797, 0.0818, 0.2838]]],grad_fn=<StackBackward>)
hn 的值
print("hn (最后一个时间步的隐藏状态):")
print(hn)
输出示例:
tensor([[[ 0.4656, 0.6676, 0.8696, 0.0717, 0.2737],[ 0.4757, 0.6777, 0.8797, 0.0818, 0.2838]],[[ 0.4858, 0.6878, 0.8898, 0.0919, 0.2939],[ 0.4959, 0.6979, 0.8999, 0.1020, 0.3040]]],grad_fn=<StackBackward>)
batch_first=True时
以下是一个具体的例子,展示当 batch_first=True 时,PyTorch 中 torch.nn.RNN 的输入、输出以及参数的作用。
任务
假设有一个简单的任务:
- 处理一个长度为 4 的序列
- 批次大小为 2
- 每个时间步的输入特征维度为 3
- 希望使用一个 2 层的单向 RNN
- 隐藏状态维度为 5
- 并且设置
batch_first=True。
2. 输入数据
输入句子
- 句子 1: “I love PyTorch”
- 句子 2: “RNN is fun”
输入数据的形状
- 批次大小 (
batch_size): 2 - 序列长度 (
seq_len): 4(假设每个单词是一个时间步) - 输入特征维度 (
input_size): 3(假设每个单词用一个 3 维向量表示)
具体输入数据
import torch# 输入数据形状: (batch_size, seq_len, input_size)
input_data = torch.tensor([# 句子 1[[0.1, 0.2, 0.3], # 第一个单词[0.7, 0.8, 0.9], # 第二个单词[1.3, 1.4, 1.5], # 第三个单词[1.9, 2.0, 2.1]], # 第四个单词# 句子 2[[0.4, 0.5, 0.6], # 第一个单词[1.0, 1.1, 1.2], # 第二个单词[1.6, 1.7, 1.8], # 第三个单词[2.2, 2.3, 2.4]] # 第四个单词
])
print("Input shape:", input_data.shape) # 输出: torch.Size([2, 4, 3])
3. 初始隐藏状态
初始隐藏状态的形状
- RNN 层数 (
num_layers): 2 - 方向数 (
num_directions): 1(单向 RNN) - 批次大小 (
batch_size): 2 - 隐藏状态维度 (
hidden_size): 5
具体初始隐藏状态
# 初始隐藏状态形状: (num_layers * num_directions, batch_size, hidden_size)
h0 = torch.zeros(2, 2, 5) # 2层RNN,批次大小为2,隐藏状态维度为5
print("h0 shape:", h0.shape) # 输出: torch.Size([2, 2, 5])
4. 定义 RNN 模型
import torch.nn as nn# 定义 RNN
rnn = nn.RNN(input_size=3, # 输入特征维度hidden_size=5, # 隐藏状态维度num_layers=2, # RNN 层数batch_first=True # 输入形状为 (batch_size, seq_len, input_size)
)
5. 前向传播
计算输出
# 前向传播
output, hn = rnn(input_data, h0)print("Output shape:", output.shape) # 输出: torch.Size([2, 4, 5])
print("hn shape:", hn.shape) # 输出: torch.Size([2, 2, 5])
输出解析
-
output:- 形状为
(batch_size, seq_len, hidden_size),即(2, 4, 5)。 - 包含了每个时间步的隐藏状态。
- 例如,
output[0]是第一个句子的所有时间步的隐藏状态,output[1]是第二个句子的所有时间步的隐藏状态。
- 形状为
-
hn:- 形状为
(num_layers, batch_size, hidden_size),即(2, 2, 5)。 - 包含了最后一个时间步的隐藏状态。
- 例如,
hn[0]是第一层的最终隐藏状态,hn[1]是第二层的最终隐藏状态。
- 形状为
6. 具体输出值
output 的值
print("Output (所有时间步的隐藏状态):")
print(output)
输出示例:
tensor([[[ 0.1234, 0.5678, 0.9101, 0.1121, 0.3141],[ 0.4252, 0.6272, 0.8292, 0.0313, 0.2333],[ 0.4454, 0.6474, 0.8494, 0.0515, 0.2535],[ 0.4656, 0.6676, 0.8696, 0.0717, 0.2737]],[[ 0.4151, 0.6171, 0.8191, 0.0212, 0.2232],[ 0.4353, 0.6373, 0.8393, 0.0414, 0.2434],[ 0.4555, 0.6575, 0.8595, 0.0616, 0.2636],[ 0.4757, 0.6777, 0.8797, 0.0818, 0.2838]]],grad_fn=<TransposeBackward0>)
hn 的值
print("hn (最后一个时间步的隐藏状态):")
print(hn)
输出示例:
tensor([[[ 0.4656, 0.6676, 0.8696, 0.0717, 0.2737],[ 0.4757, 0.6777, 0.8797, 0.0818, 0.2838]],[[ 0.4858, 0.6878, 0.8898, 0.0919, 0.2939],[ 0.4959, 0.6979, 0.8999, 0.1020, 0.3040]]],grad_fn=<StackBackward>)
相关文章:

多层 RNN原理以及实现
数学原理 多层 RNN 的核心思想是堆叠多个 RNN 层,每一层的输出作为下一层的输入,从而逐层提取更高层次的抽象特征。 1. 单层 RNN 的数学表示 首先,单层 RNN 的计算过程如下。对于一个时间步 t t t,单层 RNN 的隐藏状态 h t h_t…...

[Computer Vision]实验三:图像拼接
目录 一、实验内容 二、实验过程及结果 2.1 单应性变换 2.2 RANSAC算法 三、实验小结 一、实验内容 理解单应性变换中各种变换的原理(自由度),并实现图像平移、旋转、仿射变换等操作,输出对应的单应性矩阵。利用RANSAC算法优…...
)
【Vim Masterclass 笔记22】S09L40 + L41:同步练习11:Vim 的配置与 vimrc 文件的相关操作(含点评课内容)
文章目录 S09L40 Exercise 11 - Vim Settings and the Vimrc File1 训练目标2 操作指令2.1. 打开 vimrc-sample 文件2.2. 尝试各种选项与设置2.3. 将更改内容保存到 vimrc-sample 文件2.4. 将文件 vimrc-sample 的内容复制到寄存器2.5. 创建专属 vimrc 文件2.6. 对于 Mac、Linu…...
模块的 “时光记录仪”)
5.9 洞察 OpenAI - Translator:日志(Logger)模块的 “时光记录仪”
洞察 OpenAI - Translator:日志(Logger)模块的 “时光记录仪” 在开发和生产环境中,日志记录是确保应用程序正常运行和快速调试的核心机制之一。日志模块(Logger)用于记录应用程序的运行信息,包括错误、警告、调试信息、信息性事件等。通过日志,开发者可以实时监控程序…...
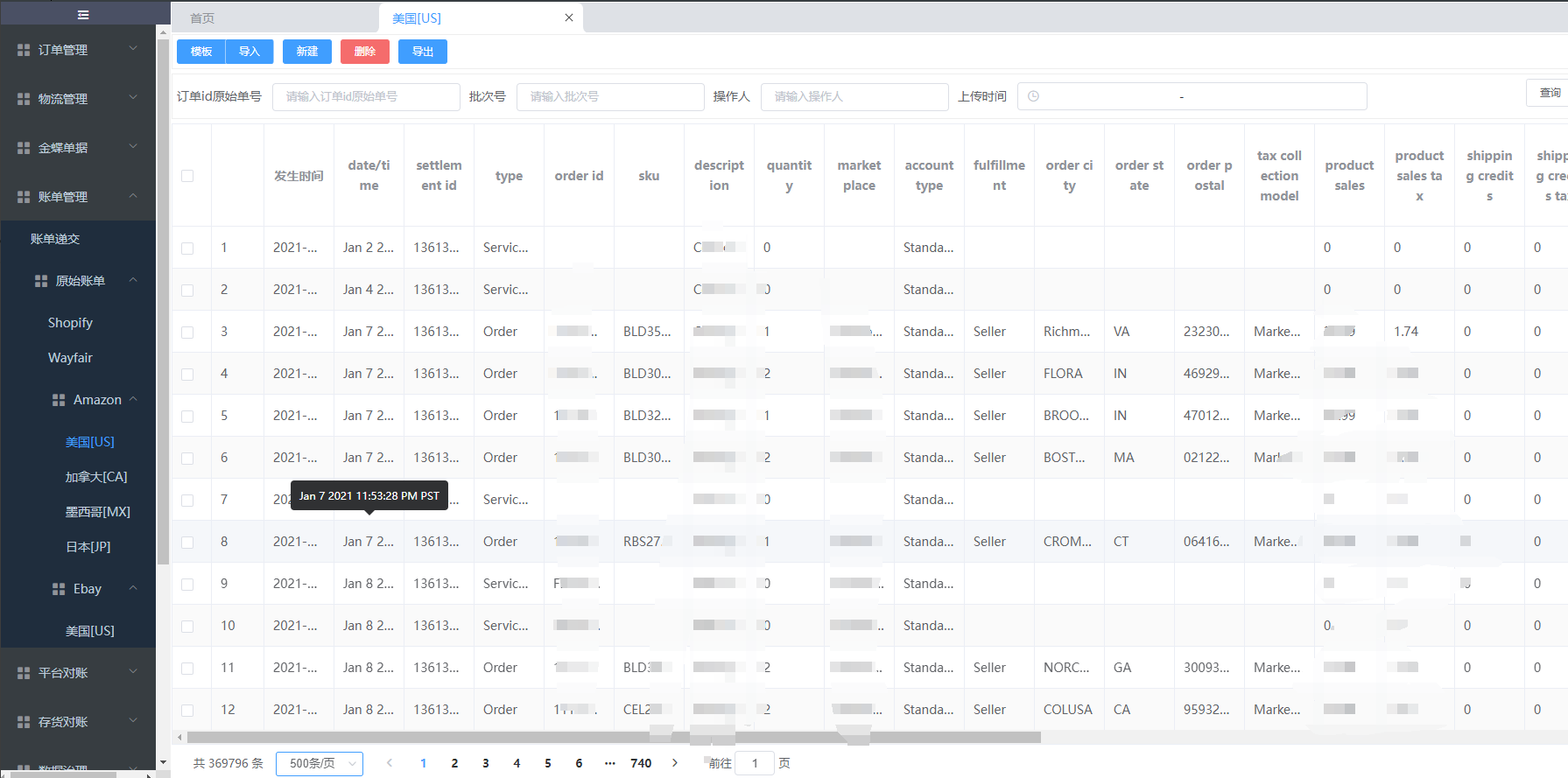
客户案例:电商平台对帐-账单管理(亚马逊amazon)
账单管理: 功能定义: 账单管理用于上传亚马逊(amazon)平台下载的原始账单数据,美国站、日本站、墨西哥站等账单模板直接进行数据上传,做到0调整,下载下来的账单数据无缝上传至对账平台-账单管…...

IP协议特性
在网络层中,最重要的协议就是IP协议,IP协议也有两个特性,即地址管理和路由选择。 1、地址管理 由于IPv4地址为4个字节,所以最多可以支持42亿个地址,但在现在,42亿明显不够用了。这就衍生出下面几个机制。…...

Kubernetes入门学习
kubernetes技术架构模型 一、kubernetes的Label标签 1.标签是以keyvalue的格式通过用户自定义指定,目的是将其加入到各种资源对象上来实现多维度的资源分组管理使其更方便的进行资源分配、调度、配置和部署管理工作。 2.标签可以结合Label Selector(标签选择器)查询…...
支持向量机SVM的应用案例
支持向量机(Support Vector Machine,SVM)是一种强大的监督学习算法,广泛应用于分类和回归任务。 基本原理 SVM的主要目标是周到一个最优的超平面,该超平面能够将不同类别的数据点尽可能分开,并且使离该超平面最近的数…...
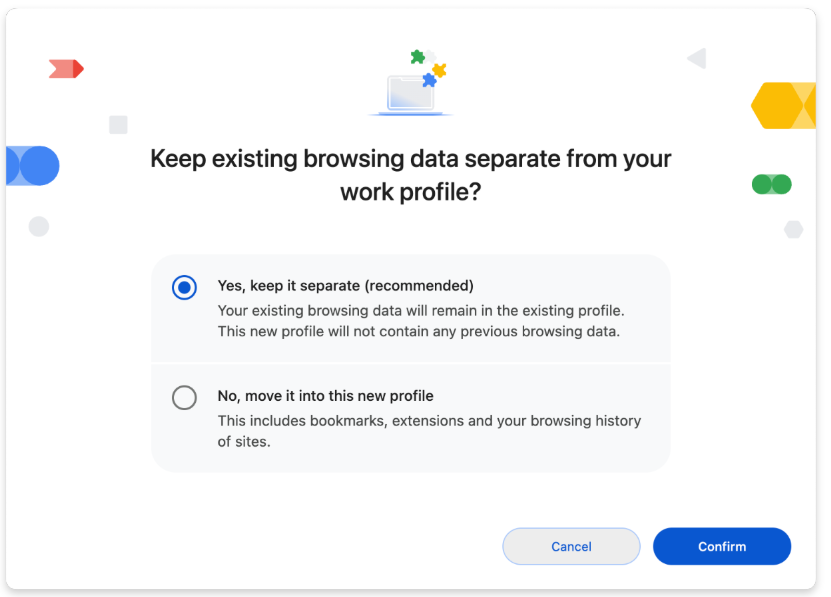
Chrome 132 版本新特性
Chrome 132 版本新特性 一、Chrome 132 版本浏览器更新 1. 在 iOS 上使用 Google Lens 搜索 在 Chrome 132 版本中,开始在所有平台上推出这一功能。 1.1. 更新版本: Chrome 126 在 ChromeOS、Linux、Mac、Windows 上:在 1% 的稳定版用户…...
(5)STM32 USB设备开发-USB键盘
讲解视频:2、USB键盘-下_哔哩哔哩_bilibili 例程:STM32USBdevice: 基于STM32的USB设备例子程序 - Gitee.com 本篇为使用使用STM32模拟USB键盘的例程,没有知识,全是实操,按照步骤就能获得一个STM32的USB键盘。本例子是…...

Linux 系统服务开机自启动指导手册
一、引言 在 Linux 系统中,设置服务开机自启动是常见的系统配置任务。本文档详细介绍了多种实现服务开机自启动的方法,包括 systemctl 方式、通用脚本方式、crontab 方案等,并提供了生产环境下的方案建议和开机启动脚本示例。 二、systemct…...

分布式多卡训练(DDP)踩坑
多卡训练最近在跑yolov10版本的RT-DETR,用来进行目标检测。 单卡训练语句(正常运行): python main.py多卡训练语句: 需要通过torch.distributed.launch来启动,一般是单节点,其中CUDA_VISIBLE…...
-C题(树上两个节点不同边数最大值))
Codeforces Round 1000 (Div. 2)-C题(树上两个节点不同边数最大值)
https://codeforces.com/contest/2063/problem/C 牢记一棵树上两个节点如果相邻,它们有一条边会重叠,两个节点延伸出去的所有不同边是两个节点入度之和-1而不是入度之和,那么如果这棵树上有三个节点它们的入度都相同,那么优先选择非相邻的两个节点才能使所有不同边的数量最大!!…...

C++17 新特性解析:Lambda 捕获 this
C17 引入了许多改进和新特性,其中之一是对 lambda 表达式的增强。在这篇文章中,我们将深入探讨 lambda 表达式中的一个特别有用的新特性:通过 *this 捕获当前对象的副本。这个特性不仅提高了代码的安全性,还极大地简化了某些场景下…...

Spring Boot 使用 Micrometer 集成 Prometheus 监控 Java 应用性能
在Spring Boot中使用Micrometer集成Prometheus来监控Java应用性能是一种常见的做法。 一、Micrometer简介 Micrometer是一个开源的Java项目,主要用于为JVM应用程序提供监控和度量功能。以下是对Micrometer的详细介绍: 定义与功能 Micrometer是一个针…...

Spring Boot 事件驱动:构建灵活可扩展的应用
在 Spring Boot 应用中,事件发布和监听机制是一种强大的工具,它允许不同的组件之间以松耦合的方式进行通信。这种机制不仅可以提高代码的可维护性和可扩展性,还能帮助我们构建更加灵活、响应式的应用。本文将深入探讨 Spring Boot 的事件发布…...

IM系统设计
读多写少,一般采用写扩散成timeline来做 写扩散模式 利用last message id作为这个作为最后一个消息体 timeline和批量未读和ack 利用ZSET来维护连接的定时心跳,来续约运营商的连接不断开...

华为EC6110T-海思Hi3798MV310_安卓9.0_通刷-强刷固件包
华为EC6110T-海思Hi3798MV310_安卓9.0_通刷-强刷固件包 刷机教程说明: 适用机型:华为EC6110-T、华为EC6110-U、华为EC6110-M 破解总分为两个部分:拆机短接破解(保留IPTV)和OTT卡刷(不保留IPTV)…...

ASP.NET Blazor托管模型有哪些?
今天我们来说说Blazor的三种部署方式,如果大家还不了解Blazor,那么我先简单介绍下Blazor Blazor 是一种 .NET 前端 Web 框架,在单个编程模型中同时支持服务器端呈现和客户端交互性: ● 使用 C# 创建丰富的交互式 UI。 ● 共享使用…...
利用深度学习提升广告效果)
PyTorch广告点击率预测(CTR)利用深度学习提升广告效果
目录 广告点击率预测问题数据集结构广告点击率预测模型的构建1. 数据集准备2. 构建数据加载器3. 构建深度学习模型4. 训练与评估 总结 广告点击率预测(CTR,Click-Through Rate Prediction)是在线广告领域中的重要任务,它帮助广告平…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
